10.E: Geometria Analítica (Exercícios)
- Page ID
- 189366
10.1: A elipse
Nesta seção, investigaremos a forma desta sala e suas aplicações no mundo real, incluindo a distância entre duas pessoas no Statuary Hall e ainda ouvirem uma à outra sussurrar.
Verbal
1) Defina uma elipse em termos de seus focos.
- Resposta
-
Uma elipse é o conjunto de todos os pontos no plano cuja soma das distâncias de dois pontos fixos, chamados focos, é uma constante.
2) Onde devem estar os focos de uma elipse?
3) Que caso especial da elipse temos quando os eixos maior e menor têm o mesmo comprimento?
- Resposta
-
Esse caso especial seria um círculo.
4) Para o caso especial mencionado acima, o que seria verdade sobre os focos dessa elipse?
5) O que se pode dizer sobre a simetria do gráfico de uma elipse com centro na origem e focos ao longo do\(y\) eixo -?
- Resposta
-
É simétrico em relação ao\(x\) eixo\(y\) -, eixo -e à origem.
Algébrico
Para os exercícios 6-10, determine se as equações dadas representam elipses. Se sim, escreva em formato padrão.
6)\(2x^2 +y=4\)
7)\(4x^2 + 9y^2=36\)
- Resposta
-
sim;\(\dfrac{x^2}{3^2}+\dfrac{y^2}{2^2}=1\)
8)\(4x^2 - y^2=4\)
9)\(4x^2 + 9y^2=1\)
- Resposta
-
sim;\(\dfrac{x^2}{\left (\tfrac{1}{2} \right )^2}+\dfrac{y^2}{\left (\tfrac{1}{2} \right )^2}=1\)
10)\(4x^2-8x+9y^2-72y+112=0\)
Para os exercícios 11-26, escreva a equação de uma elipse na forma padrão e identifique os pontos finais dos eixos maior e menor, bem como os focos.
11)\(\dfrac{x^2}{4}+\dfrac{y^2}{49}=1\)
- Resposta
-
\(\dfrac{x^2}{2^2}+\dfrac{y^2}{7^2}=1\); Extremidades do eixo principal\((0,7)\)\((0,-7)\) e. Extremidades do eixo menor\((2,0)\)\((-2,0)\) e. Foco em\((0, 3\sqrt{5})\),\((0, -3\sqrt{5})\).
12)\(\dfrac{x^2}{100}+\dfrac{y^2}{64}=1\)
13)\(x^2 + 9y^2 = 1\)
- Resposta
-
\(\dfrac{x^2}{(1)^2}+\dfrac{y^2}{\left (\tfrac{1}{3} \right )^2}=1\); Extremidades do eixo principal\((1,0)\)\((-1,0)\) e. Extremidades do eixo menor\(\left (0, \dfrac{1}{3} \right )\),\(\left (0, -\dfrac{1}{3} \right )\). Foco em\(\left (\dfrac{2\sqrt{2}}{3}, 0 \right )\),\(\left (-\dfrac{2\sqrt{2}}{3}, 0 \right )\).
14)\(4x^2 + 16y^2 = 1\)
15)\(\dfrac{(x-2)^2}{49}+\dfrac{(y-4)^2}{25}=1\)
- Resposta
-
\(\dfrac{(x-2)^2}{7^2}+\dfrac{(y-4)^2}{5^2}=1\); Extremidades do eixo principal\((9,4)\),\((-5,4)\). Extremidades do eixo menor\((2,9)\),\((2,-1)\). Foco em\((2+2\sqrt{6}, 4)\),\((2-2\sqrt{6}, 4)\)
16)\(\dfrac{(x-2)^2}{81}+\dfrac{(y+1)^2}{16}=1\)
17)\(\dfrac{(x+5)^2}{4}+\dfrac{(y-7)^2}{9}=1\)
- Resposta
-
\(\dfrac{(x+5)^2}{2^2}+\dfrac{(y-7)^2}{3^2}=1\); Extremidades do eixo principal\((-5,10)\),\((-5,4)\). Extremidades do eixo menor\((-3,7)\),\((-7,7)\). Foco em\((-5, 7+\sqrt{5})\),\((-5, 7-\sqrt{5})\)
18)\(\dfrac{(x-7)^2}{49}+\dfrac{(y-7)^2}{49}=1\)
19)\(4x^2-8x+9y^2-72y+112=0\)
- Resposta
-
\(\dfrac{(x-1)^2}{3^2}+\dfrac{(y-4)^2}{2^2}=1\); Extremidades do eixo principal\((4,4)\),\((-2,4)\). Extremidades do eixo menor\((1,6)\),\((1,2)\). Foco em\((1+\sqrt{5}, 4)\),\((1-\sqrt{5}, 4)\)
20)\(9x^2-54x+9y^2-54y+81=0\)
21)\(4x^2-24x+36y^2-360y+864=0\)
- Resposta
-
\(\dfrac{(x-3)^2}{(3\sqrt{2})^2}+\dfrac{(y-5)^2}{\sqrt{2}^2}=1\); Extremidades do eixo principal\((3+3\sqrt{2}, 5)\),\((3-3\sqrt{2}, 5)\). Extremidades do eixo menor\((3, 5+\sqrt{2})\),\((3, 5-\sqrt{2})\). Foco em\((7,5)\),\((-1,5)\)
22)\(4x^2+24x+16y^2-128y+228=0\)
23)\(4x^2+40x+25y^2-100y+100=0\)
- Resposta
-
\(\dfrac{(x+5)^2}{(5)^2}+\dfrac{(y-2)^2}{(2)^2}=1\); Extremidades do eixo principal\((0,2)\),\((-10,2)\). Extremidades do eixo menor\((-5,4)\),\((-5,0)\). Foco em\((-5+\sqrt{21}, 2)\),\((-5-\sqrt{21}, 2)\)
24)\(x^2+2x+100y^2-1000y+2401=0\)
25)\(4x^2+24x+25y^2+200y+336=0\)
- Resposta
-
\(\dfrac{(x+3)^2}{(5)^2}+\dfrac{(y+4)^2}{(2)^2}=1\); Extremidades do eixo principal\((2,-4)\),\((-8,-4)\). Extremidades do eixo menor\((-3,-2)\),\((-3,-6)\). Foco em\((-3+\sqrt{21}, -4)\),\((-3-\sqrt{21}, -4)\)
26)\(9x^2+72x+16y^2+16y+4=0\)
Para os exercícios 27-31, encontre os focos das elipses dadas.
27)\(\dfrac{(x+3)^2}{25}+\dfrac{(y+1)^2}{36}=1\)
- Responda
-
Focos\((-3, -1+\sqrt{11})\),\((-3, -1-\sqrt{11})\)
28)\(\dfrac{(x+1)^2}{100}+\dfrac{(y-2)^2}{4}=1\)
29)\(x^2+y^2=1\)
- Responda
-
Foco\((0,0)\)
30)\(x^2+4y^2+4x+8y=1\)
31)\(10x^2+y^2+200x=0\)
- Responda
-
Focos\((-10,30)\),\((-10,-30)\)
Gráfica
Para os exercícios 32-45, represente graficamente as elipses dadas, observando o centro, os vértices e os focos.
32)\(\dfrac{x^2}{25}+\dfrac{y^2}{36}=1\)
33)\(\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\)
- Responda
-
Centro\((0,0)\), Vértices\((4,0)\)\((-4,0)\),,\((0,3)\),\((0,-3)\). Focos\((\sqrt{7},0)\),\((-\sqrt{7},0)\)
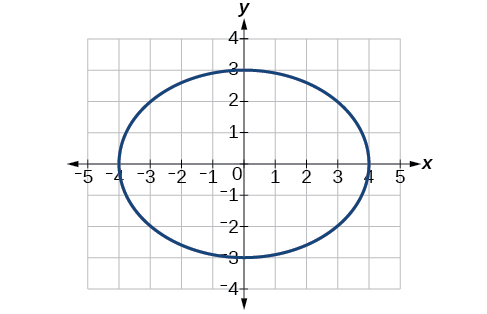
34)\(4x^2+9y^2=1\)
35)\(81x^2+49y^2=1\)
- Responda
-
Centro\((0,0)\), Vértices\(\left ( \dfrac{1}{9}, 0 \right )\)\(\left ( -\dfrac{1}{9}, 0 \right )\),,\(\left ( 0, \dfrac{1}{7} \right )\),\(\left ( 0, \dfrac{1}{7} \right )\). Focos\(\left ( 0, \dfrac{4\sqrt{2}}{63} \right )\),\(\left ( 0, -\dfrac{4\sqrt{2}}{63} \right )\)
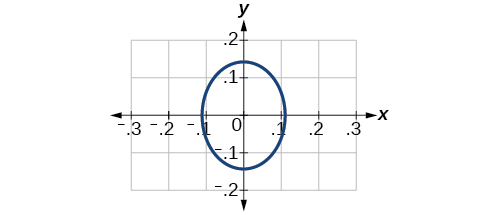
36)\(\dfrac{(x-2)^2}{64}+\dfrac{(y-4)^2}{16}=1\)
37)\(\dfrac{(x+3)^2}{9}+\dfrac{(y-3)^2}{9}=1\)
- Responda
-
Centro\((-3,3)\), Vértices\((0,3)\)\((-6,3)\),,\((-3,0)\),\((-3,6)\). Foco\((-3,3)\)
Note que essa elipse é um círculo. O círculo tem apenas um foco, que coincide com o centro.
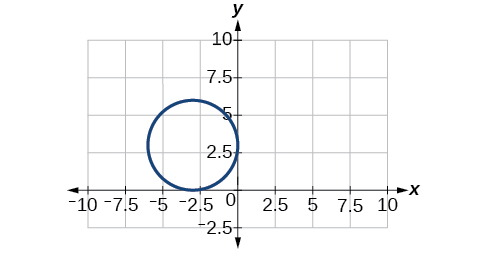
38)\(\dfrac{x^2}{2}+\dfrac{(y+1)^2}{5}=1\)
39)\(4x^2-8x+16y^2-32y-44=0\)
- Responda
-
Centro\((1,1)\), Vértices\((5,1)\)\((-3,1)\),,\((1,3)\),\((1,-1)\). Focos\((1,1+4\sqrt{3})\),\((1,1-4\sqrt{3})\)
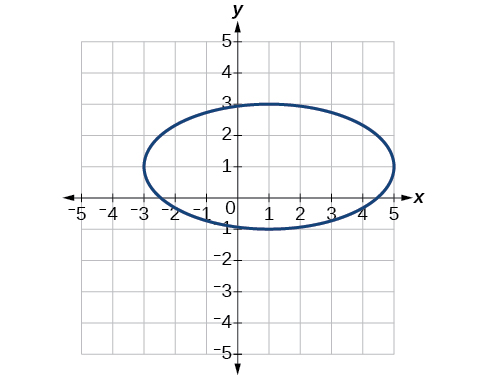
40)\(x^2-8x+25y^2-100y+91=0\)
41)\(x^2+8x+4y^2-40y+112=0\)
- Responda
-
Centro\((-4,5)\), Vértices\((-2,5)\)\((-6,4)\),,\((-4,6)\),\((-4,4)\). Focos\((-4+\sqrt{3}, 5)\),\((-4-4\sqrt{3}, 5)\)
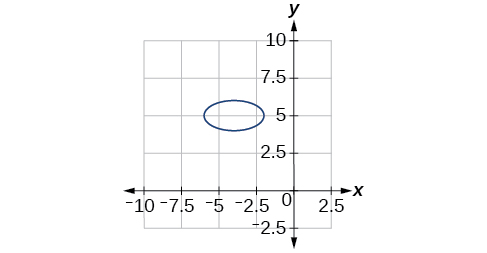
42)\(64x^2+128x+9y^2-72y-368=0\)
43)\(16x^2+64x+4y^2-8y+4=0\)
- Responda
-
Centro\((-2,1)\), Vértices\((0,1)\)\((-4,1)\),,\((-2,5)\),\((-2,-3)\). Focos\((-2,1+2\sqrt{3})\),\((-2,1-2\sqrt{3})\)
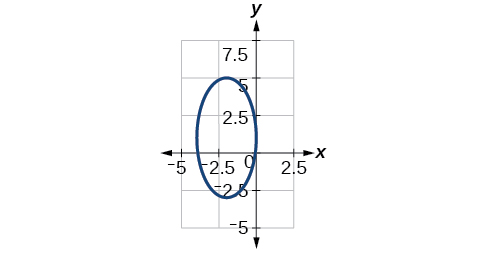
44)\(100x^2+1000x+y^2-10y+2425=0\)
45)\(4x^2+16x+4y^2+16y+16=0\)
- Responda
-
Centro\((-2,2)\), Vértices\((0,-2)\)\((-4,-2)\),,\((-2,0)\),\((-2,-4)\). Foco\((-2,-2)\)
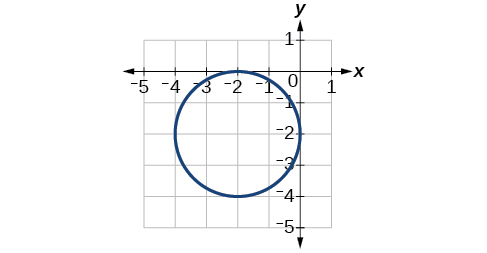
Para os exercícios 46-51, use as informações fornecidas sobre o gráfico de cada elipse para determinar sua equação.
46) Centralize na origem, simétrico em relação aos\(y\) eixos\(x\) - e -, foque em\((4,0)\) um ponto no gráfico\((0,3)\).
47) Centralize na origem, simétrico em relação aos\(y\) eixos\(x\) - e -, foque em\((0,-2)\) um ponto no gráfico\((5,0)\).
- Responda
-
\(\dfrac{x^2}{25}+\dfrac{y^2}{29}=1\)
48) Centro na origem, simétrico em relação aos\(y\) eixos\(x\) - e -, foco em\((3,0)\), e o eixo maior é duas vezes maior que o eixo menor.
49) Centro\((4,2)\); vértice\((9,2)\); um foco:\((4+2\sqrt{6}, 2)\)
- Responda
-
\(\dfrac{(x-4)^2}{25}+\dfrac{(y-2)^2}{1}=1\)
50) Centro\((3,5)\); vértice\((3,11)\); um foco:\((3, 5+4\sqrt{2})\)
51) Centro\((-3,4)\); vértice\((1,4)\); um foco:\((-3+2\sqrt{3}, 4)\)
- Responda
-
\(\dfrac{(x+3)^2}{16}+\dfrac{(y-4)^2}{4}=1\)
Para os exercícios 52-56, dado o gráfico da elipse, determine sua equação.
52)
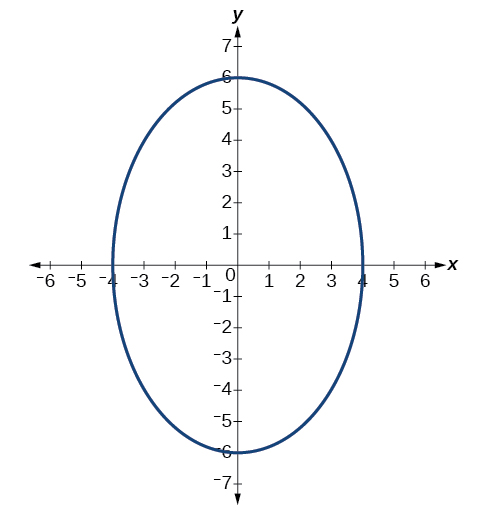
53)
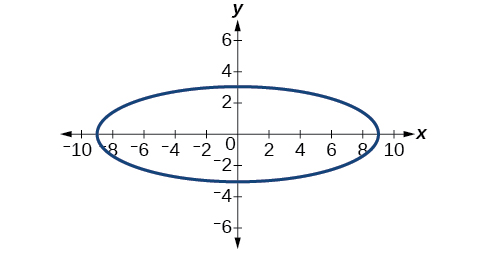
- Responda
-
\(\dfrac{x^2}{81}+\dfrac{y^2}{9}=1\)
54)
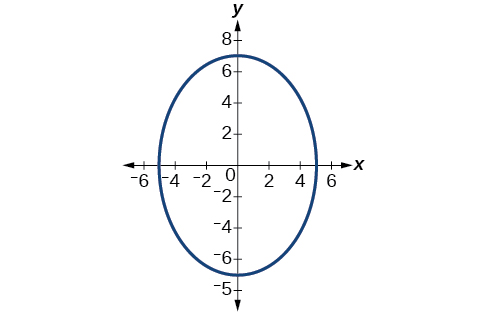
55)
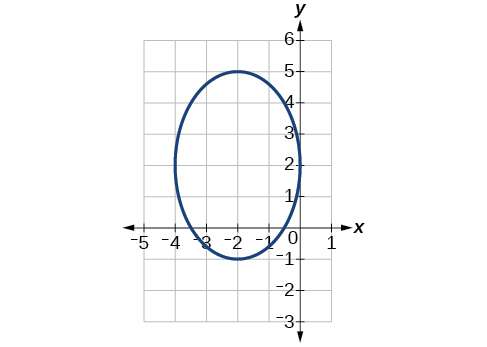
- Responda
-
\(\dfrac{(x+2)^2}{4}+\dfrac{(y-2)^2}{9}=1\)
56)
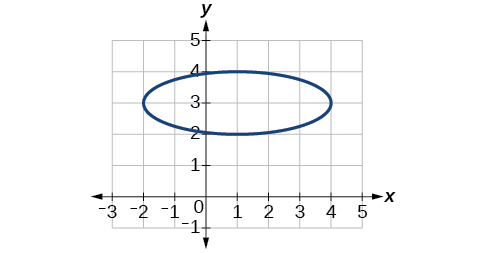
Extensões
Para os exercícios 57-61, encontre a área da elipse. A área de uma elipse é dada pela fórmula\(\text {Area}=a\cdot b\cdot \pi\)
57)\(\dfrac{(x-3)^2}{9}+\dfrac{(y-3)^2}{16}=1\)
- Responda
-
\(\text {Area} = 12\pi \)unidades quadradas
(58)\(\dfrac{(x+6)^2}{16}+\dfrac{(y-6)^2}{36}=1\)
59)\(\dfrac{(x+1)^2}{4}+\dfrac{(y-2)^2}{5}=1\)
- Responda
-
\(\text {Area} = 2\sqrt{5} \pi \)unidades quadradas
60)\(4x^2-8x+9y^2-72y+112=0\)
61)\(9x^2-54x+9y^2-54y+81=0\)
- Responda
-
\(\text {Area} = 9\pi \)unidades quadradas
Aplicativos do mundo real
62) Encontre a equação da elipse que caberá apenas dentro de uma caixa com\(8\) unidades de largura e\(4\) unidades de altura.
63) Encontre a equação da elipse que caberá dentro de uma caixa que é quatro vezes maior que a altura. Expresse em termos de\(h\) altura.
- Responda
-
\(\dfrac{x^2}{4h^2}+\dfrac{y^2}{\tfrac{1}{4}h^2}=1\)
64) Um arco tem a forma de uma semi-elipse (a metade superior de uma elipse). O arco tem uma altura de\(8\) pés e uma extensão de\(20\) pés. Encontre uma equação para a elipse e use-a para encontrar a altura do\(0.01\) pé mais próximo do arco a uma distância de\(4\) pés do centro.
65) Um arco tem a forma de uma semi-elipse. O arco tem uma altura de\(12\) pés e uma extensão de\(40\) pés. Encontre uma equação para a elipse e use-a para encontrar a distância do centro até um ponto em que a altura seja\(6\) pés. Arredonde para o centésimo mais próximo.
- Responda
-
\(\dfrac{x^2}{400}+\dfrac{y^2}{144}=1\). Distância =\(17.32\) pés
66) Uma ponte deve ser construída na forma de um arco semi-elíptico e deve ter uma extensão de\(120\) pés. A altura do arco a uma distância de\(40\) pés do centro deve ser de\(8\) pés. Encontre a altura do arco em seu centro.
67) Uma pessoa em uma galeria sussurrante parada em um foco da elipse pode sussurrar e ser ouvida por uma pessoa parada no outro foco porque todas as ondas sonoras que atingem o teto são refletidas para a outra pessoa. Se uma galeria sussurrante tiver um comprimento de\(120\) pés e os focos estiverem localizados a\(30\) pés do centro, encontre a altura do teto no centro.
- Responda
-
Aproximadamente\(51.96\) pés
68) Uma pessoa está a poucos\(8\) metros da parede mais próxima em uma galeria sussurrante. Se essa pessoa está em um foco e o outro está a\(80\) pés de distância, qual é o comprimento e a altura no centro da galeria?
10.2: A hipérbole
Em geometria analítica, uma hipérbole é uma seção cônica formada pela interseção de um cone circular reto com um plano em um ângulo de forma que ambas as metades do cone sejam cruzadas. Essa interseção produz duas curvas separadas e ilimitadas que são imagens espelhadas uma da outra.
Verbal
1) Defina uma hipérbole em termos de seus focos.
- Responda
-
Uma hipérbole é o conjunto de pontos em um plano cuja diferença de distâncias de dois pontos fixos (focos) é uma constante positiva.
2) O que podemos concluir sobre uma hipérbole se suas assíntotas se cruzam na origem?
3) O que deve ser verdade sobre os focos de uma hipérbole?
- Responda
-
Os focos devem estar no eixo transversal e estar no interior da hipérbole.
4) Se o eixo transversal de uma hipérbole for vertical, o que sabemos sobre o gráfico?
5) Onde o centro da hipérbole deve estar em relação aos seus focos?
- Responda
-
O centro deve ser o ponto médio do segmento de linha que une os focos.
Algébrico
Para os exercícios 6-10, determine se as equações a seguir representam hipérboles. Em caso afirmativo, escreva em formato padrão.
6)\(3y^2 + 2x = 6\)
7)\(\dfrac{x^2}{36}-\dfrac{y^2}{9}=1\)
- Responda
-
sim\(\dfrac{x^2}{6^2}-\dfrac{y^2}{3^2}=1\)
8)\(5y^2 + 4x^2 = 6x\)
9)\(25x^2 - 16y^2 = 400\)
- Responda
-
sim\(\dfrac{x^2}{4^2}-\dfrac{y^2}{5^2}=1\)
10)\(-9x^2+18x+y^2+4y-14=0\)
Para os exercícios 11-25, escreva a equação da hipérbole na forma padrão, se ainda não estiver, identifique os vértices e focos e escreva as equações das assíntotas.
11)\(\dfrac{x^2}{25}-\dfrac{y^2}{36}=1\)
- Responda
-
\(\dfrac{x^2}{5^2}-\dfrac{y^2}{6^2}=1\); vértices:\((5,0)\),\((-5,0)\); focos:\((\sqrt{61},0)\),\((-\sqrt{61},0)\); assíntotas:\(y=\dfrac{6}{5}x\),\(y=-\dfrac{6}{5}x\)
12)\(\dfrac{x^2}{100}-\dfrac{y^2}{9}=1\)
13)\(\dfrac{y^2}{4}-\dfrac{x^2}{81}=1\)
- Responda
-
\(\dfrac{y^2}{2^2}-\dfrac{x^2}{9^2}=1\); vértices:\((0,2)\),\((0,-2)\); focos:\((0,\sqrt{85})\),\((0,-\sqrt{85})\); assíntotas:\(y=\dfrac{2}{9}x\),\(y=-\dfrac{2}{9}x\)
14)\(9y^2 - 4x^2 = 1\)
15)\(\dfrac{(x-1)^2}{9}-\dfrac{(y-2)^2}{16}=1\)
- Responda
-
\(\dfrac{(x-1)^2}{3^2}-\dfrac{(y-2)^2}{4^2}=1\); vértices:\((4,2)\),\((-2,2)\); focos:\((6,2)\),\((-4,2)\); assíntotas:\(y=\dfrac{4}{3}(x-1)+2\),\(y=-\dfrac{4}{3}(x-1)+2\)
16)\(\dfrac{(y-6)^2}{36}-\dfrac{(x+1)^2}{16}=1\)
17)\(\dfrac{(x-2)^2}{49}-\dfrac{(y+7)^2}{49}=1\)
- Responda
-
\(\dfrac{(x-2)^2}{7^2}-\dfrac{(y+7)^2}{7^2}=1\); vértices:\((9,-7)\),\((-5,-7)\); focos:\((2+7\sqrt{2},-7)\),\((2-7\sqrt{2},-7)\); assíntotas:\(y=x-9\),\(y=-x-5\)
18)\(4x^2-8x-9y^2-72y+112=0\)
19)\(-9x^2-54x+9y^2-54y+81=0\)
- Responda
-
\(\dfrac{(x+3)^2}{3^2}-\dfrac{(y-3)^2}{3^2}=1\); vértices:\((0,3)\),\((-6,3)\); focos:\((-3+3\sqrt{2},1)\),\((-3-3\sqrt{2},1)\); assíntotas:\(y=x+6\),\(y=-x\)
20)\(4x^2-24x-36y^2-360y+864=0\)
21)\(-4x^2+24x+16y^2-128y+156=0\)
- Responda
-
\(\dfrac{(y-4)^2}{2^2}-\dfrac{(x-3)^2}{4^2}=1\); vértices:\((3,6)\),\((3,2)\); focos:\((3,4+2\sqrt{5})\),\((3,4-2\sqrt{5})\); assíntotas:\(y=\dfrac{1}{2}(x-3)+4\),\(y=-\dfrac{1}{2}(x-3)+4\)
22)\(-4x^2+40x+25y^2-100y+100=0\)
23)\(x^2+2x-100y^2-1000y+2401=0\)
- Responda
-
\(\dfrac{(y+5)^2}{7^2}-\dfrac{(x+1)^2}{70^2}=1\); vértices:\((-1,2)\),\((-1,-12)\); focos:\((-1,-5+7\sqrt{101})\),\((-1,-5-7\sqrt{101})\); assíntotas:\(y=\dfrac{1}{10}(x+1)-5\),\(y=-\dfrac{1}{10}(x+1)-5\)
24)\(-9x^2+72x+16y^2+16y+4=0\)
25)\(4x^2+24x-25y^2+200y-464=0\)
- Responda
-
\(\dfrac{(x+3)^2}{5^2}-\dfrac{(y-4)^2}{2^2}=1\); vértices:\((2,4)\),\((-8,4)\); focos:\((-3+\sqrt{29},4)\),\((-3-\sqrt{29},4)\); assíntotas:\(y=\dfrac{2}{5}(x+3)+4\),\(y=-\dfrac{2}{5}(x+3)+4\)
Para os exercícios 26-30, encontre as equações das assíntotas para cada hipérbole.
26)\(\dfrac{y^2}{3^2}-\dfrac{x^2}{3^2}=1\)
27)\(\dfrac{(x-3)^2}{5^2}-\dfrac{(y+4)^2}{2^2}=1\)
- Responda
-
\(y=\dfrac{2}{5}(x-3)-4\),\(y=-\dfrac{2}{5}(x-3)-4\)
28)\(\dfrac{(y-3)^2}{3^2}-\dfrac{(x+5)^2}{6^2}=1\)
29)\(9x^2-18x-16y^2+32y-151=0\)
- Responda
-
\(y=\dfrac{3}{4}(x-1)+1\),\(y=-\dfrac{3}{4}(x-1)+1\)
30)\(16y^2+96y-4x^2+16x+112=0\)
Gráfica
Para os exercícios 31-44, esboce um gráfico da hipérbole, rotulando vértices e focos.
31)\(\dfrac{x^2}{49}-\dfrac{y^2}{16}=1\)
- Responda
-
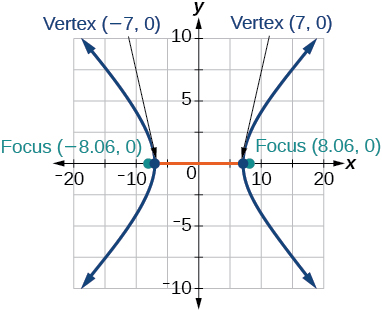
32)\(\dfrac{x^2}{64}-\dfrac{y^2}{4}=1\)
33)\(\dfrac{y^2}{9}-\dfrac{x^2}{25}=1\)
- Responda
-
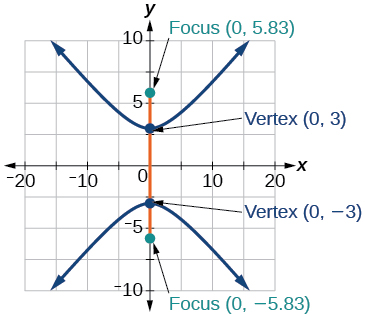
34)\(81x^2-9y^2=1\)
(35)\(\dfrac{(y+5)^2}{9}-\dfrac{(x-4)^2}{25}=1\)
- Responda
-
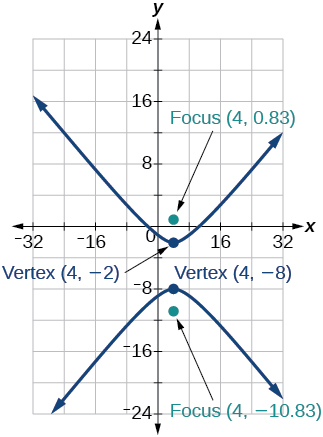
36)\(\dfrac{(x-2)^2}{8}-\dfrac{(y+3)^2}{27}=1\)
37)\(\dfrac{(y-3)^2}{9}-\dfrac{(x-3)^2}{9}=1\)
- Responda
-
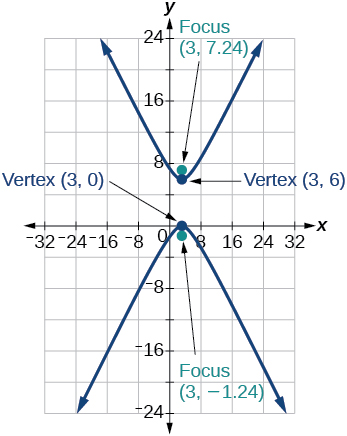
38)\(-4x^2-8x+16y^2-32y-52=0\)
39)\(x^2-8x-25y^2-100y-109=0\)
- Responda
-
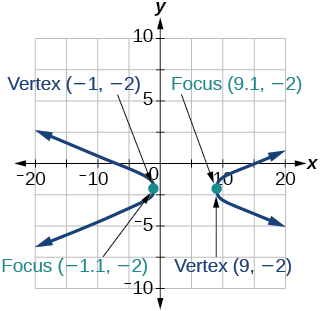
40)\(-x^2+8x+4y^2-40y+88=0\)
41)\(64x^2+128x-9y^2-72y-656=0\)
- Responda
-
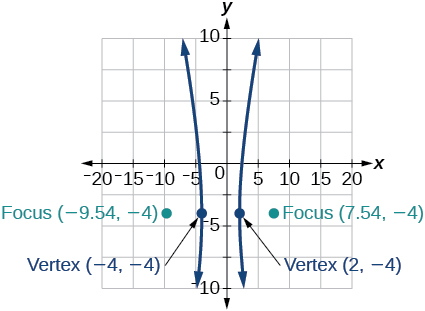
(42)\(16x^2+64x-4y^2-8y-4=0\)
43)\(-100x^2+1000x+y^2-10y-2575=0\)
- Responda
-
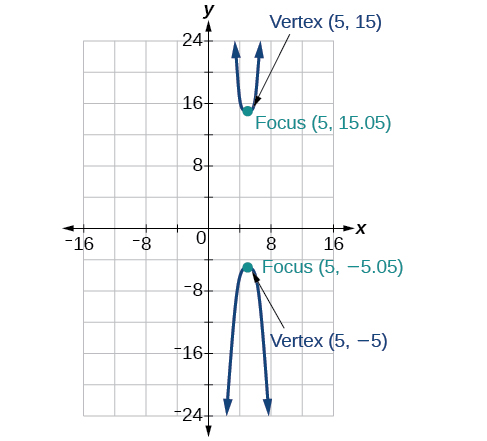
44)\(4x^2+16x-4y^2+16y+16=0\)
Para os exercícios 45-50, dadas as informações sobre o gráfico da hipérbole, encontre sua equação.
45) Vértices em\((3,0)\)\((-3,0)\) e e um foco em\((5,0)\).
- Responda
-
\(\dfrac{x^2}{9}-\dfrac{y^2}{16}=1\)
46) Vértices em\((0,6)\)\((0,-6)\) e e um foco em\((0,-8)\).
47) Vértices em\((1,1)\)\((11,1)\) e e um foco em\((12,1)\).
- Responda
-
\(\dfrac{(x-6)^2}{25}-\dfrac{(y-1)^2}{11}=1\)
48) Centro:\((0,0)\); vértice:\((0,-13)\)
49) Centro:\((4,2)\); vértice:\((9,2)\)
- Responda
-
\(\dfrac{(x-4)^2}{25}-\dfrac{(y-2)^2}{1}=1\)
50) Centro:\((3,5)\); vértice:\((3,11)\); um foco:\((3,5+2\sqrt{10})\).
Para os exercícios 51-,55, dado o gráfico da hipérbole, encontre sua equação.
51)
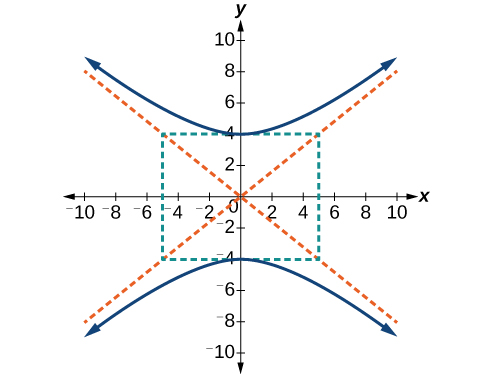
- Responda
-
\(\dfrac{y^2}{16}-\dfrac{x^2}{25}=1\)
52)
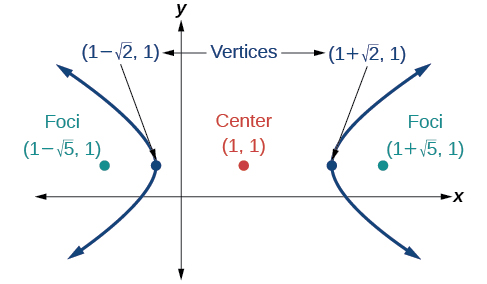
53)
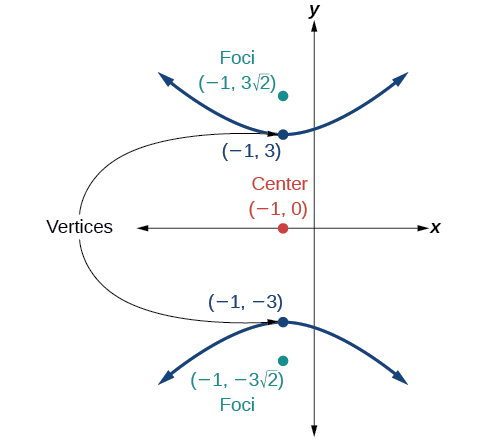
- Responda
-
\(\dfrac{y^2}{9}-\dfrac{(x+1)^2}{9}=1\)
54)
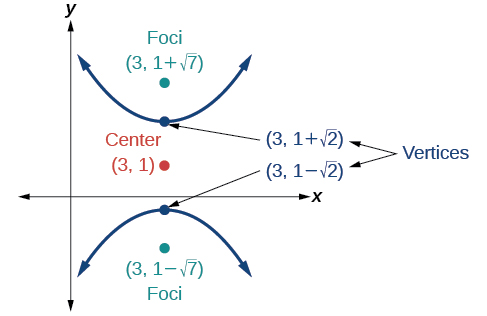
55)
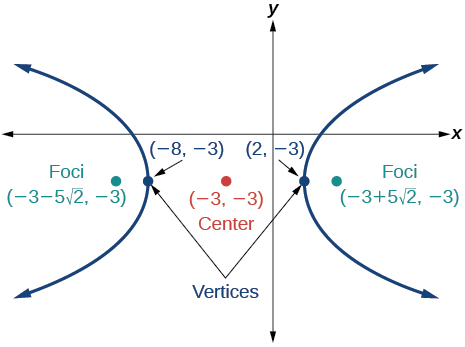
- Responda
-
\(\dfrac{(x+3)^2}{25}-\dfrac{(y+3)^2}{25}=1\)
Extensões
Para os exercícios 56-60, expresse a equação da hipérbole como duas funções, com\(y\) como função de\(x\). Expresse da forma mais simples possível. Use uma calculadora gráfica para esboçar o gráfico das duas funções nos mesmos eixos.
56)\(\dfrac{x^2}{4}-\dfrac{y^2}{9}=1\)
57)\(\dfrac{y^2}{9}-\dfrac{x^2}{1}=1\)
- Responda
-
\(y(x)=3\sqrt{x^2 +1}\),\(y(x)=-3\sqrt{x^2 +1}\)
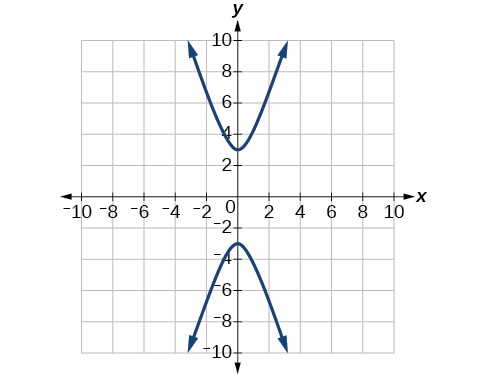
(58)\(\dfrac{(x-2)^2}{16}-\dfrac{(y+3)^2}{25}=1\)
(59)\(-4x^2-16x+y^2-2y-19=0\)
- Responda
-
\(y(x)=1+2\sqrt{x^2 +4x+5}\),\(y(x)=1-2\sqrt{x^2 +4x+5}\)
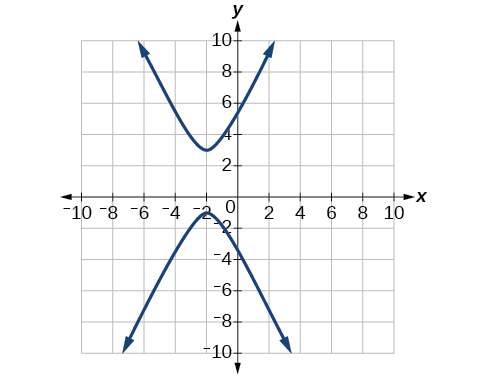
60)\(4x^2-24x-y^2-4y+16=0\)
Aplicativos do mundo real
Para os exercícios 61-65, uma sebe deve ser construída em forma de hipérbole perto de uma fonte no centro do pátio. Encontre a equação da hipérbole e desenhe o gráfico.
61) A sebe seguirá as assíntotas\(y=x\) e\(y=-x\), e sua distância mais próxima da fonte central é de\(5\) metros.
- Responda
-
\(\dfrac{x^2}{25}-\dfrac{y^2}{25}=1\)
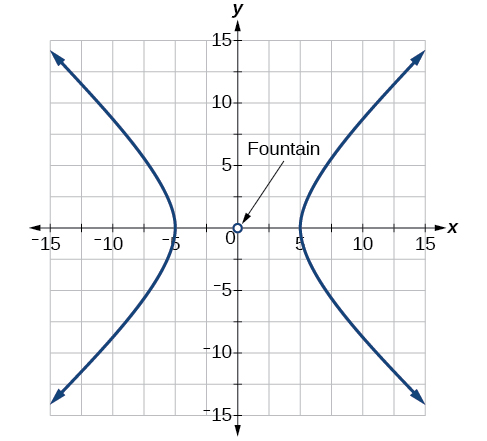
62) A sebe seguirá as assíntotas\(y=2x\) e\(y=-2x\), e sua distância mais próxima da fonte central é de\(6\) metros.
63) A sebe seguirá as assíntotas\(y=\dfrac{1}{2}x\) e\(y=-\dfrac{1}{2}x\), e sua distância mais próxima da fonte central é de\(10\) metros.
- Responda
-
\(\dfrac{x^2}{100}-\dfrac{y^2}{25}=1\)
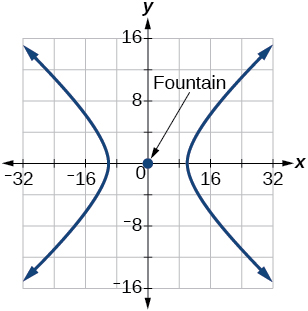
64) A sebe seguirá as assíntotas\(y=\dfrac{2}{3}x\) e\(y=-\dfrac{2}{3}x\), e sua distância mais próxima da fonte central é de\(12\) metros.
65) A sebe seguirá as assíntotas\(y=\dfrac{3}{4}x\) e\(y=-\dfrac{3}{4}x\), e sua distância mais próxima da fonte central é de\(20\) metros.
- Responda
-
\(\dfrac{x^2}{400}-\dfrac{y^2}{225}=1\)
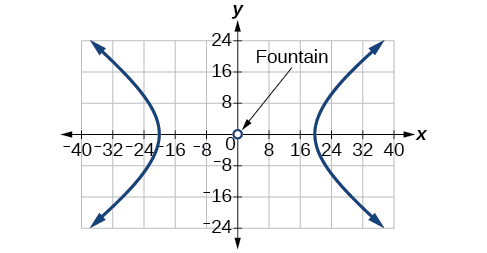
Para os exercícios 66-70, suponha que um objeto entre em nosso sistema solar e desejemos representar graficamente seu caminho em um sistema de coordenadas com o sol na origem e o\(x\) eixo -como eixo de simetria para o caminho do objeto. Dê a equação da trajetória de voo de cada objeto usando as informações fornecidas.
66) O objeto entra por um caminho aproximado pela linha\(y=x-2\) e passa dentro de\(1\) au (unidade astronômica) do sol em sua aproximação mais próxima, de modo que o sol é um dos focos da hipérbole. Em seguida, ele parte do sistema solar por um caminho aproximado pela linha\(y=−x+2\).
67) O objeto entra por um caminho aproximado pela linha\(y=2x-2\) e passa dentro\(0.5\) do sol em sua aproximação mais próxima, então o sol é um dos focos da hipérbole. Em seguida, ele parte do sistema solar por um caminho aproximado pela linha\(y=-2x+2\).
- Responda
-
\(\dfrac{(x-1)^2}{0.25}-\dfrac{y^2}{0.75}=1\)
68) O objeto entra por um caminho aproximado pela linha\(y=0.5x+2\) e passa dentro\(1\) do sol em sua aproximação mais próxima, então o sol é um dos focos da hipérbole. Em seguida, ele parte do sistema solar por um caminho aproximado pela linha\(y=−0.5x−2\).
69) O objeto entra por um caminho aproximado pela linha\(y=\dfrac{1}{3}x-1\) e passa dentro\(1\) do sol em sua aproximação mais próxima, então o sol é um dos focos da hipérbole. Em seguida, ele parte do sistema solar por um caminho aproximado pela linha\(y=-\dfrac{1}{3}x+1\).
- Responda
-
\((x-3)^2 - 9y^2 = 4\)
70) O objeto entra por um caminho aproximado pela linha\(y=3x-9\) e passa dentro\(1\) do sol em sua aproximação mais próxima, então o sol é um dos focos da hipérbole. Em seguida, ele parte do sistema solar por um caminho aproximado pela linha\(y=−3x+9\).
10.3: A parábola
Como a elipse e a hipérbole, a parábola também pode ser definida por um conjunto de pontos no plano coordenado. Uma parábola é o conjunto de todos os pontos em um plano que estão à mesma distância de uma linha fixa, chamada diretriz, e um ponto fixo (o foco) que não está na diretriz.
Verbal
1) Defina uma parábola em termos de seu foco e diretriz.
- Responda
-
Uma parábola é o conjunto de pontos no plano que se encontram equidistantes de um ponto fixo, o foco, e uma linha fixa, a diretriz.
2) Se a equação de uma parábola for escrita na forma padrão e\(p\) for positiva e a diretriz for uma linha vertical, o que podemos concluir sobre seu gráfico?
3) Se a equação de uma parábola for escrita na forma padrão e\(p\) for negativa e a diretriz for uma linha horizontal, o que podemos concluir sobre seu gráfico?
- Responda
-
O gráfico será aberto.
4) Qual é o efeito no gráfico de uma parábola se sua equação na forma padrão tiver valores crescentes de\(p\)?
5) À medida que o gráfico de uma parábola se torna mais amplo, o que acontecerá com a distância entre o foco e a diretriz?
- Responda
-
A distância entre o foco e a diretriz aumentará.
Algébrico
Para os exercícios 6-10, determine se a equação dada é uma parábola. Em caso afirmativo, reescreva a equação na forma padrão.
6)\(y^2=4-x^2\)
7)\(y=4x^2\)
- Responda
-
sim\(y=4(1)x^2\)
8)\(3x^2-6y^2=12\)
9)\((y-3)^2=8(x-2)\)
- Responda
-
sim\((y-3)^2=4(2)(x-2)\)
10)\(y^2+12x-6y-51=0\)
Para os exercícios 11-30, reescreva a equação dada na forma padrão e, em seguida, determine o vértice\((V)\)\((F)\), o foco e a diretriz\((d)\) da parábola.
11)\(x=8y^2\)
- Responda
-
\(y^2=\dfrac{1}{8}x\),\(V:(0,0)\),\(F:\left (\dfrac{1}{32},0 \right )\),\(d:x=-\dfrac{1}{32}\)
12)\(y=\dfrac{1}{4}x^2\)
13)\(y=-4x^2\)
- Responda
-
\(x^2=-\dfrac{1}{4}y\),\(V:(0,0)\),\(F:\left (0,-\dfrac{1}{16} \right )\),\(d:y=-\dfrac{1}{16}\)
14)\(x=\dfrac{1}{8}y^2\)
15)\(x=36y^2\)
- Responda
-
\(y^2=\dfrac{1}{36}x\),\(V:(0,0)\),\(F:\left (\dfrac{1}{144},0 \right )\),\(d:x=-\dfrac{1}{144}\)
16)\(x=\dfrac{1}{36}y^2\)
17)\((x-1)^2=4(y-1)\)
- Responda
-
\((x-1)^2=4(y-1)\),\(V:(1,1)\),\(F:(1,2)\),\(d:y=0\)
18)\((y-2)^2=\dfrac{4}{5}(x+4)\)
19)\((y-4)^2=2(x+3)\)
- Responda
-
\((y-4)^2=2(x+3)\),\(V:(-3,4)\),\(F:\left (-\dfrac{5}{2},4 \right )\),\(d:x=-\dfrac{7}{2}\)
20)\((x+1)^2=2(y+4)\)
21)\((x+4)^2=24(y+1)\)
- Responda
-
\((x+4)^2=24(y+1)\),\(V:(-4,-1)\),\(F:(-4,5)\),\(d:y=-7\)
22)\((y+4)^2=16(x+4)\)
23)\(y^2+12x-6y+21=0\)
- Responda
-
\((y-3)^2=-12(x+1)\),\(V:(-1,3)\),\(F:(-4,3)\),\(d:x=2\)
24)\(x^2-4x-24y+28=0\)
25)\(5x^2-50x-4y+113=0\)
- Responda
-
\((x-5)^2=\dfrac{4}{5}(y+3)\),\(V:(5,-3)\),\(F:\left (5,-\dfrac{14}{5} \right )\),\(d:y=-\dfrac{16}{5}\)
26)\(y^2-24x+4y-68=0\)
27)\(x^2-4x+2y-6=0\)
- Responda
-
\((x-2)^2=-2(y-5)\),\(V:(2,5)\),\(F:\left (2,\dfrac{9}{2} \right )\),\(d:y=\dfrac{11}{2}\)
28)\(y^2-6y+12x-3=0\)
29)\(3y^2-4x-6y+23=0\)
- Responda
-
\((y-1)^2=\dfrac{4}{3}(x-5)\),\(V:(5,1)\),\(F:\left (\dfrac{16}{3},1 \right )\),\(d:x=\dfrac{14}{3}\)
30)\(x^2+4x+8y-4=0\)
Gráfica
Para os exercícios 31-44, represente graficamente a parábola, rotulando o foco e a diretriz.
31)\(x=\dfrac{1}{8}y^2\)
- Responda
-
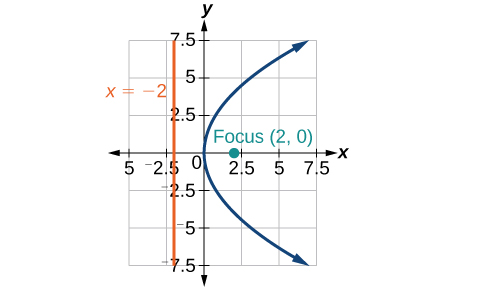
32)\(y=36x^2\)
33)\(y=\dfrac{1}{36}x^2\)
- Responda
-
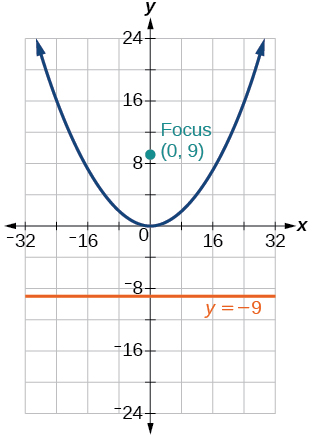
34)\(y=-9x^2\)
(35)\((y-2)^2=-\dfrac{4}{3}(x+2)\)
- Responda
-
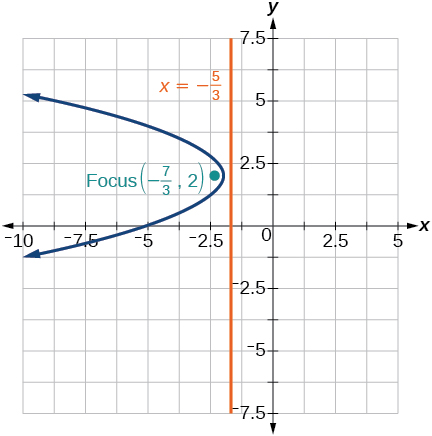
36)\(-5(x+5)^2=4(y+5)\)
37)\(-6(y+5)^2=4(x-4)\)
- Responda
-
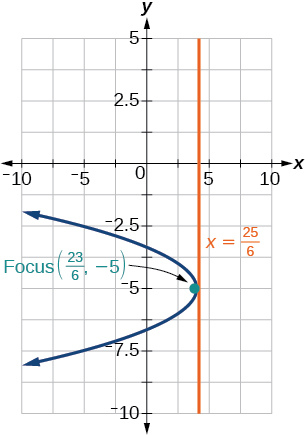
38)\(y^2-6y-8x+1=0\)
39)\(x^2+8x+4y+20=0\)
- Responda
-
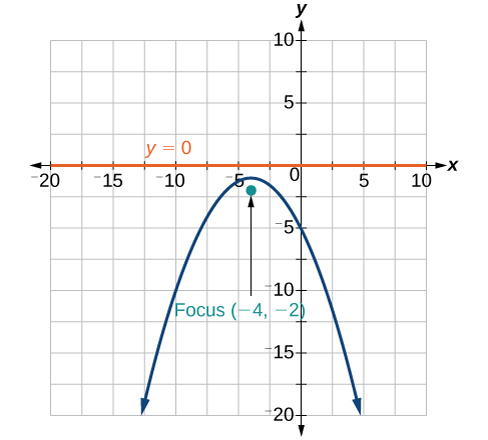
40)\(3x^2+30x-4y+95=0\)
41)\(y^2-8x+10y+9=0\)
- Responda
-
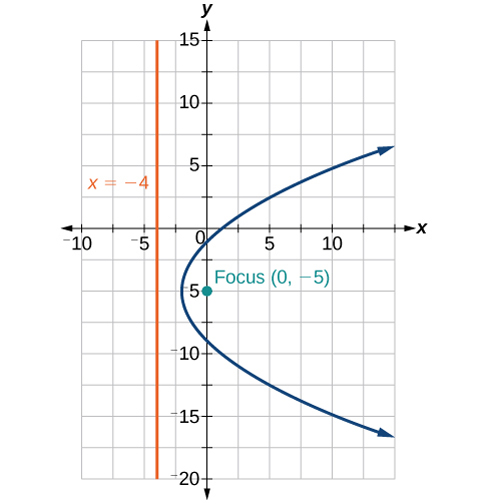
(42)\(x^2+4x+2y+2=0\)
43)\(y^2+2y-12x+61=0\)
- Responda
-
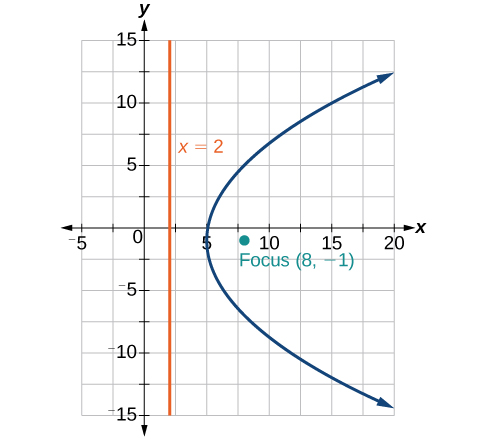
44)\(-2x^2+8x-4y-24=0\)
Para os exercícios 45-50, encontre a equação da parábola com as informações sobre seu gráfico.
45) O vértice é\((0,0)\); a diretriz é\(y=4\), o foco é\((0,-4)\).
- Responda
-
\(x^2=-16y\)
46) O vértice é\((0,0)\); a diretriz é\(x=4\), o foco é\((-4,0)\).
47) Vértice é\((2,2)\); diretriz é\(x=2-\sqrt{2}\), foco é\((2+\sqrt{2},2)\).
- Responda
-
\((y-2)^2 = 4\sqrt{2}(x-2)\)
48) O vértice é\((-2,3)\); a diretriz é\(x=-\dfrac{7}{2}\), o foco é\( \left(-\dfrac{1}{2},3 \right)\).
49) O vértice é\((\sqrt{2},-\sqrt{3})\); a diretriz é\(x=2\sqrt{2}\), o foco é\((0,-\sqrt{3})\).
- Responda
-
\((y+\sqrt{3})^2 = -4\sqrt{2}(x-\sqrt{2})\)
50) O vértice é\((-,21)\); a diretriz é\(y=\dfrac{11}{3}\), o foco é\( \left(1,\dfrac{1}{3} \right)\).
Para os exercícios 51-55, determine a equação da parábola a partir de seu gráfico.
51)
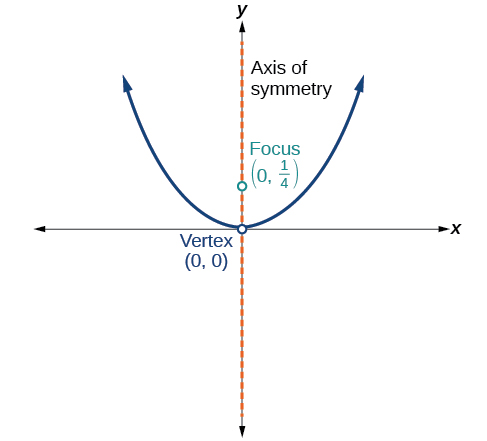
- Responda
-
\(x^2=y\)
52)
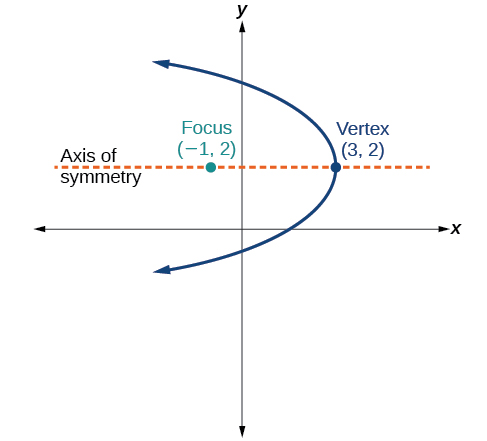
53)
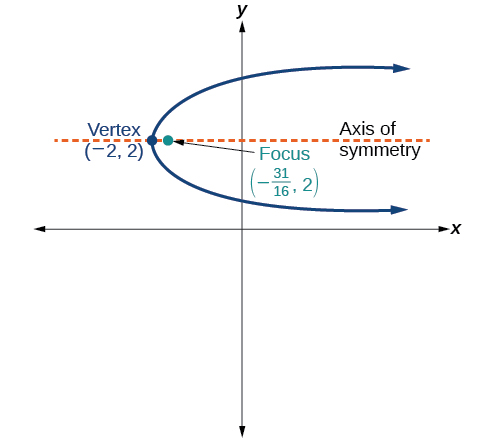
- Responda
-
\((y-2)^2 = \dfrac{1}{4}(x+2)\)
54)
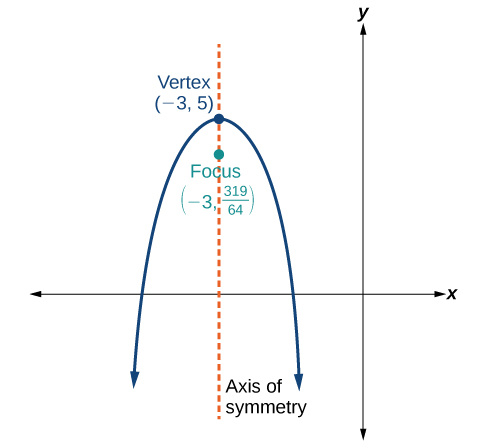
55)
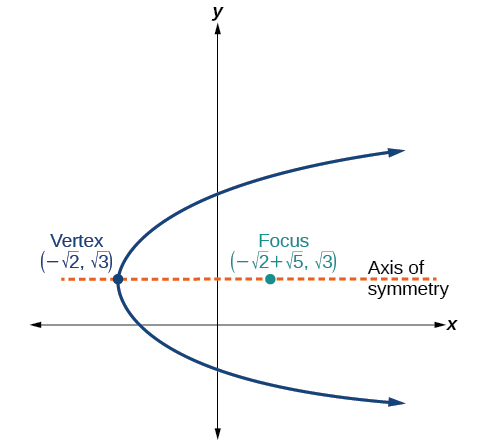
- Responda
-
\((y-\sqrt{2})^2 = 4\sqrt{5}(x+\sqrt{2})\)
Extensões
Para os exercícios 56-60, são fornecidos o vértice e os pontos finais do latus reto de uma parábola. Encontre a equação.
56)\(V(0,0)\), Extremidades\((2,1),(−2,1)\)
57)\(V(0,0)\), Extremidades\((-2,4),(−2,-4)\)
- Responda
-
\(y^2=-8x\)
(58)\(V(1,2)\), Endpoints \((-5,5),(7,5)\)
(59)\(V(-3,-1)\), Endpoints \((0,5),(0,-7)\)
- Responda
-
\((y+1)^2 = 12(x+3)\)
60)\(V(4,-3)\), Endpoints \(\left ( 5,-\dfrac{7}{2} \right ), \left ( 3,-\dfrac{7}{2} \right )\)
Aplicativos do mundo real
61) O espelho do farol de um automóvel tem uma seção transversal parabólica com a lâmpada no foco. Em um esquema, a equação da parábola é dada como\(x^2=4y\). Em quais coordenadas você deve colocar a lâmpada?
- Responda
-
\((0,1)\)
62) Se quisermos construir o espelho a partir do exercício anterior de forma que o foco esteja localizado em\((0,0.25)\) qual deve ser a equação da parábola?
63) Uma antena parabólica tem a forma de um parabolóide da revolução. Isso significa que ela pode ser formada girando uma parábola em torno de seu eixo de simetria. O receptor deve estar localizado no foco. Se o prato tiver\(12\) pés de largura na abertura e\(4\) pés de profundidade no centro, onde o receptor deve ser colocado?
- Responda
-
No ponto,\(2.25\) pés acima do vértice.
64) Considere a antena parabólica do exercício anterior. Se o prato tiver\(8\) pés de largura na abertura e\(2\) pés de profundidade, onde devemos colocar o receptor?
65) Um holofote tem a forma de um parabolóide da revolução. Uma fonte de luz está localizada a\(1\) pé da base ao longo do eixo de simetria. Se a abertura do holofote tiver\(3\) pés de diâmetro, encontre a profundidade.
- Responda
-
\(0.5625\)pés
66) Se o holofote do exercício anterior tiver a fonte de luz localizada a\(6\) centímetros da base ao longo do eixo de simetria e a abertura for\(4\) pés, encontre a profundidade.
67) Um arco tem a forma de uma parábola. Tem uma extensão de\(100\) pés e uma altura máxima de\(20\) pés. Encontre a equação da parábola e determine a altura dos\(40\) pés do arco a partir do centro.
- Responda
-
\(x^2=-125(y-20)\), a altura é\(7.2\) pés
68) Se o arco do exercício anterior tiver uma envergadura de\(160\) pés e uma altura máxima de\(40\) pés, encontre a equação da parábola e determine a distância do centro em que a altura é\(20\) pés.
69) Um objeto é projetado de forma a seguir um caminho parabólico dado por\(y=-x^2+96x\) onde\(x\) está a distância horizontal percorrida em pés e\(y\) é a altura. Determine a altura máxima que o objeto atinge.
- Responda
-
\(2304\)pés
70) Para o objeto do exercício anterior, suponha que o caminho seguido seja dado por\(y=-0.5x^2+80x\). Determine até que ponto o objeto percorreu na horizontal até atingir a altura máxima.
10.4: Rotação dos eixos
Nas seções anteriores deste capítulo, nos concentramos nas equações de forma padrão para seções cônicas não degeneradas. Nesta seção, vamos mudar nosso foco para a equação geral da forma, que pode ser usada para qualquer cônica. A forma geral é definida como igual a zero, e os termos e coeficientes são fornecidos em uma ordem específica, conforme mostrado abaixo.
Verbal
1) Que efeito o\(xy\) termo tem no gráfico de uma seção cônica?
- Responda
-
O\(xy\) termo faz com que ocorra uma rotação do gráfico.
2) Se a equação de uma seção cônica estiver escrita na forma\(Ax^2+By^2+Cx+Dy+E=0\) e\(AB=0\) o que podemos concluir?
3) Se a equação de uma seção cônica estiver escrita na forma\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\)\(B^2-4AC>0\), e o que podemos concluir?
- Responda
-
A seção cônica é uma hipérbole.
4) Dada a equação\(ax^2+4x+3y^2-12=0\), o que podemos concluir se\(a>0\)?
5) Para a equação,\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) o valor\(\theta \) que satisfaz nos\(\cot (2\theta )=\dfrac{A-C}{B}\) fornece quais informações?
- Responda
-
Ele fornece o ângulo de rotação dos eixos para eliminar o\(xy\) termo.
Algébrico
Para os exercícios 6-17, determine qual seção cônica é representada com base na equação dada.
6)\(9x^2+4y^2+72x+36y-500=0\)
7)\(x^2-10x+4y-10=0\)
- Responda
-
\(AB=0\), parábola
8)\(2x^2-2y^2+4x-6y-2=0\)
9)\(4x^2-y^2+8x-1=0\)
- Responda
-
\(AB=-4<0\), hipérbole
10)\(4y^2-5x+9y+1=0\)
11)\(2x^2+3y^2-8x-12y+2=0\)
- Responda
-
\(AB=6>0\), elipse
12)\(4x^2+9xy+4y^2-36y-125=0\)
13)\(3x^2+6xy+3y^2-36y-125=0\)
- Responda
-
\(B^2 - 4AC=0\), parábola
14)\(-3x^2+3\sqrt{3}xy-4y^2+9=0\)
15)\(2x^2+4\sqrt{3}xy+6y^2-6x-3=0\)
- Responda
-
\(B^2 - 4AC=0\), parábola
16)\(-x^2+4\sqrt{2}xy+2y^2-2y+1=0\)
17)\(8x^2+4\sqrt{2}xy+4y^2-10x+1=0\)
- Responda
-
\(B^2 - 4AC=-96<0\), elipse
Para os exercícios 18-22, encontre uma nova representação da equação dada depois de girar através do ângulo dado.
18)\(3x^2+xy+3y^2-5=0, \theta =45^{\circ}\)
19)\(4x^2-xy+4y^2-2=0, \theta =45^{\circ}\)
- Responda
-
\(7x'^2+9y'^2-4=0\)
20)\(2x^2+8xy-1=0, \theta =30^{\circ}\)
21)\(-2x^2+8xy+1=0, \theta =45^{\circ}\)
- Responda
-
\(3x'^2+2x'y'-5y'^2+1=0\)
22)\(4x^2+\sqrt{2}xy+4y^2+y+2=0, \theta =45^{\circ}\)
Para os exercícios 23-30, determine o ângulo\(\theta \) que eliminará o\(xy\) termo e escreva a equação correspondente sem o\(xy\) termo.
23)\(x^2+3\sqrt{3}xy+4y^2+y-2=0\)
- Responda
-
\(\theta =60^{\circ},11x'^2-y'2+\sqrt{3}x'+y'-4=0\)
24)\(4x^2+2\sqrt{3}xy+6y^2+y-2=0\)
25)\(9x^2-3\sqrt{3}xy+6y^2+4y-3=0\)
- Responda
-
\(\theta =150^{\circ},21x'^2+9y'^2+4x'-4\sqrt{3}y'-6=0\)
26)\(-3x^2-\sqrt{3}xy-2y^2-x=0\)
27)\(16x^2+24xy+9y^2+6x-6y+2=0\)
- Responda
-
\(\theta \approx 36.9^{\circ},125x'^2+6x'-42y'+10=0\)
28)\(x^2+4xy+4y^2+3x-2=0\)
29)\(x^2+4xy+y^2-2x+1=0\)
- Responda
-
\(\theta =45^{\circ},3x'^2-y'^2-\sqrt{2}x'+\sqrt{2}y'+1=0\)
30)\(4x^2-2\sqrt{3}xy+6y^2-1=0\)
Gráfica
Para os exercícios 31-38, gire o ângulo dado com base na equação dada. Dê a nova equação e represente graficamente a equação original e rotacionada.
31)\(y=-x^2,\theta =-45^{\circ}\)
- Responda
-
\(\dfrac{\sqrt{2}}{2}(x'+y')=\dfrac{1}{2}(x'-y')^2\)
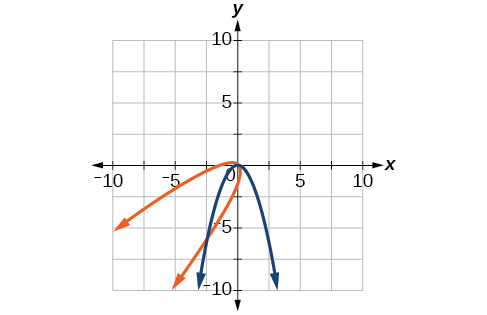
32)\(x=y^2,\theta =45^{\circ}\)
33)\(\dfrac{x^2}{4}+\dfrac{y^2}{1}=1,\theta =45^{\circ}\)
- Responda
-
\(\dfrac{(x'-y')^2}{8}+\dfrac{(x'+y')^2}{2}=1\)
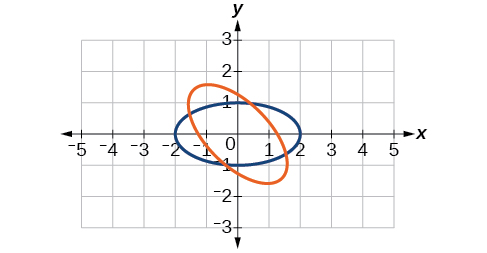
34)\(\dfrac{y^2}{16}+\dfrac{x^2}{9}=1,\theta =45^{\circ}\)
(35)\(y^2 - x^2 = 1, \theta =45^{\circ}\)
- Responda
-
\(\dfrac{(x'+y')^2}{2}-\dfrac{(x'-y')^2}{2}=1\)
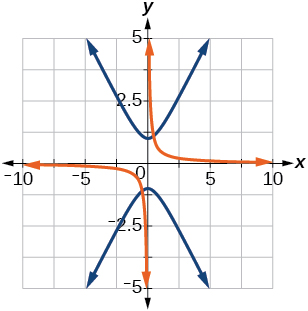
36)\(y=\dfrac{x^2}{2}, \theta =30^{\circ}\)
37)\(x=(y-1)^2, \theta =30^{\circ}\)
- Responda
-
\(\dfrac{\sqrt{3}}{2}x'-\dfrac{1}{2}y'=\left ( \dfrac{1}{2}x' + \dfrac{\sqrt{3}}{2}x' - 1 \right )^2\)
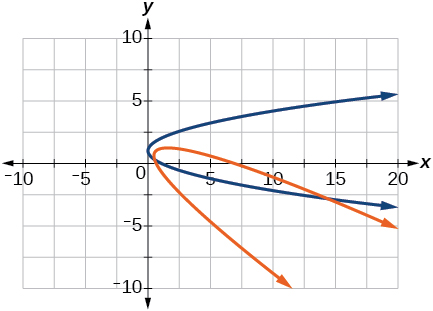
38)\(\dfrac{x^2}{9}+\dfrac{y^2}{4}=1,\theta =30^{\circ}\)
Para os exercícios 39-49, represente graficamente a equação em relação ao\(x'y'\) sistema no qual a equação não tem\(x'y'\) termo.
39)\(xy=9\)
- Responda
-
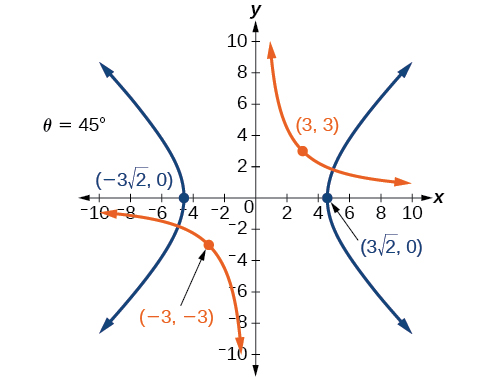
40)\(x^2+10xy+y^2-6=0\)
41)\(x^2-10xy+y^2-24=0\)
- Responda
-
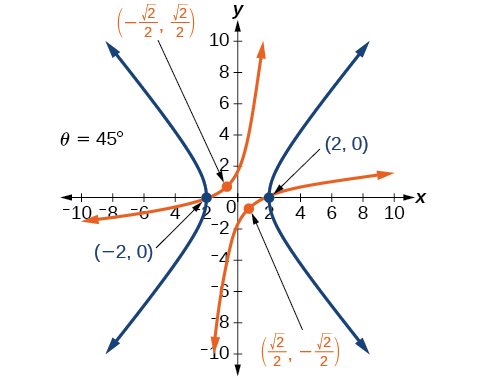
(42)\(4x^2-3\sqrt{3}xy+y^2-22=0\)
43)\(6x^2+2\sqrt{3}xy+4y^2-21=0\)
- Responda
-
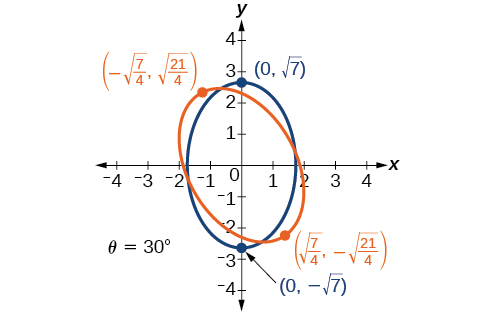
44)\(11x^2+10\sqrt{3}xy+y^2-64=0\)
45)\(21x^2+2\sqrt{3}xy+19y^2-18=0\)
- Responda
-
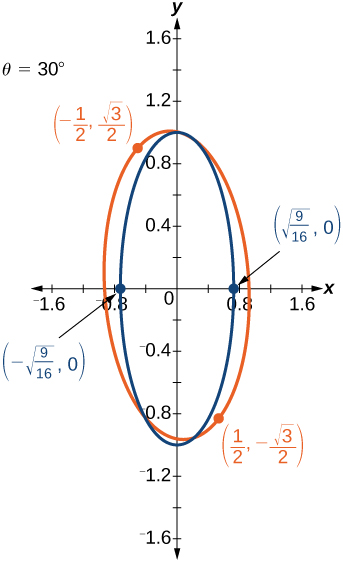
(46)\(16x^2+24xy+9y^2-130x+90y=0\)
47)\(16x^2+24xy+9y^2-60x+80y=0\)
- Responda
-
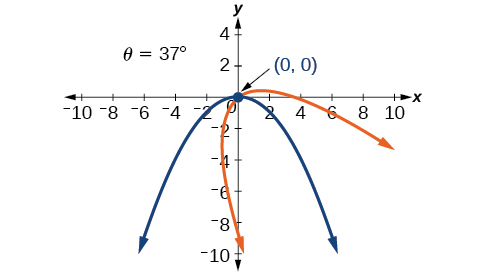
48)\(13x^2-6\sqrt{3}xy+7y^2-16=0\)
49)\(4x^2-4xy+y^2-8\sqrt{5}x-16\sqrt{5}y=0\)
- Responda
-
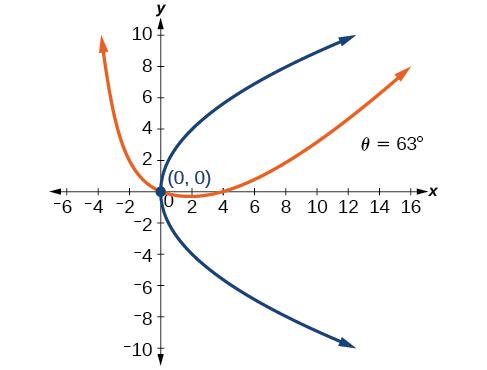
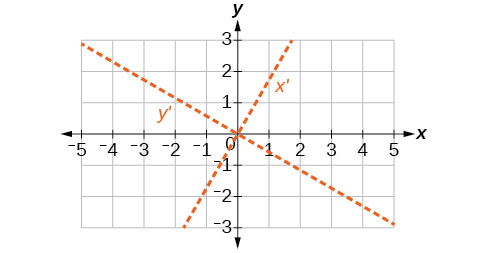
Para os exercícios 50-55, determine o ângulo de rotação para eliminar o\(xy\) termo. Em seguida, faça um gráfico do novo conjunto de eixos.
50)\(6x^2-5\sqrt{3}xy+y^2+10x-12y=0\)
51)\(6x^2-5xy+6y^2+20x-y=0\)
- Responda
-
\(\theta =45^{\circ}\)
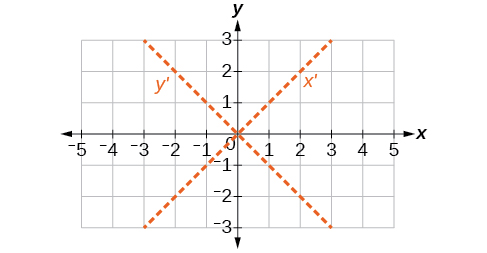
52)\(6x^2-8\sqrt{3}xy+14y^2+10x-3y=0\)
53)\(4x^2+6\sqrt{3}xy+10y^2+20x-40y=0\)
- Responda
-
\(\theta =60^{\circ}\)
54)\(8x^2+3xy+4y^2+2x-4=0\)
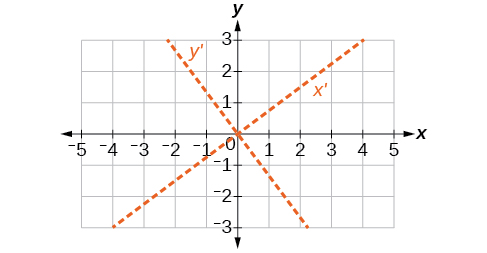
55)\(16x^2+24xy+9y^2+20x-44y=0\)
- Responda
-
\(\theta \approx 36.9^{\circ}\)
Para os exercícios 56-60, determine o valor de\(k\) com base na equação dada.
56) Dado\(4x^2+kxy+16y^2+8x+24y-48=0\),\(k\) considere que o gráfico é uma parábola.
57) Dado\(2x^2+kxy+12y^2+10x-16y+28=0\),\(k\) determine que o gráfico é uma elipse.
- Responda
-
\(-4\sqrt{6}<k<4\sqrt{6}\)
58) Dado\(3x^2+kxy+4y^2-6x+20y+128=0\), considere\(k\) que o gráfico é uma hipérbole.
59)\(kx^2+8xy+8y^2-12x+16y+18=0\) Dada\(k\) a conclusão de que o gráfico é uma parábola.
- Responda
-
\(k=2\)
60) Dada\(6x^2+12xy+ky^2+16x+10y+4=0\) a\(k\) conclusão de que o gráfico é uma elipse.
10.5: Seções cônicas em coordenadas polares
Nesta seção, aprenderemos como definir qualquer cônica no sistema de coordenadas polares em termos de um ponto fixo, o foco no polo e uma linha, a diretriz, que é perpendicular ao eixo polar.
Verbal
1) Explique como a excentricidade determina qual seção cônica é dada.
- Responda
-
Se a excentricidade for menor que\(1\), é uma elipse. Se a excentricidade for igual a\(1\), é uma parábola. Se a excentricidade for maior que\(1\), é uma hipérbole.
2) Se uma seção cônica for escrita como uma equação polar, o que deve ser verdade sobre o denominador?
3) Se uma seção cônica é escrita como uma equação polar e o denominador envolve\(\sin \theta \) que conclusão pode ser extraída sobre a diretriz?
- Responda
-
A diretriz será paralela ao eixo polar.
4) Se a diretriz de uma seção cônica é perpendicular ao eixo polar, o que sabemos sobre a equação do gráfico?
5) O que sabemos sobre o foco/focos de uma seção cônica se ela for escrita como uma equação polar?
- Responda
-
Um dos focos estará localizado na origem.
Algébrico
Para os exercícios 6-17, identifique a cônica com um foco na origem e, em seguida, forneça a diretriz e a excentricidade.
6)\(r=\dfrac{6}{1-2\cos \theta }\)
7)\(r=\dfrac{3}{4-4\sin \theta }\)
- Resposta
-
Parábola com\(e=1\)\(\dfrac{3}{4}\) unidades diretivas abaixo do polo.
8)\(r=\dfrac{8}{4-3\cos \theta }\)
9)\(r=\dfrac{5}{1+2\sin \theta }\)
- Resposta
-
Hipérbole com\(e=2\)\(\dfrac{5}{2}\) unidades diretivas acima do polo.
10)\(r=\dfrac{15}{4+3\cos \theta }\)
11)\(r=\dfrac{3}{10+10\cos \theta }\)
- Resposta
-
Parábola com\(e=1\)\(\dfrac{3}{10}\) unidades diretivas à direita do poste.
12)\(r=\dfrac{2}{1-\cos \theta }\)
13)\(r=\dfrac{4}{7+2\cos \theta }\)
- Resposta
-
Elipse com\(e=\dfrac{2}{7}\)\(2\) unidades diretriz à direita do poste.
14)\(r(1-\cos \theta )=3\)
15)\(r(3+5\sin \theta )=11\)
- Resposta
-
Hipérbole com\(e=\dfrac{5}{3}\)\(\dfrac{11}{5}\) unidades diretivas acima do polo.
16)\(r(4-5\sin \theta )=1\)
17)\(r(7+8\sin \theta )=7\)
- Resposta
-
Hipérbole com\(e=\dfrac{8}{7}\)\(\dfrac{7}{8}\) unidades diretivas à direita do poste.
Para os exercícios 18-30, converta a equação polar de uma seção cônica em uma equação retangular.
18)\(r=\dfrac{4}{1+3\sin \theta }\)
19)\(r=\dfrac{2}{5-3\sin \theta }\)
- Resposta
-
\(25x^2+16y^2-12y-4=0\)
20)\(r=\dfrac{8}{3-2\cos \theta }\)
21)\(r=\dfrac{3}{2+5\cos \theta }\)
- Resposta
-
\(21x^2-4y^2-30x+9=0\)
22)\(r=\dfrac{4}{2+2\sin \theta }\)
23)\(r=\dfrac{3}{8-8\cos \theta }\)
- Resposta
-
\(64y^2=48x+9\)
24)\(r=\dfrac{2}{6+7\cos \theta }\)
25)\(r=\dfrac{5}{5-11\sin \theta }\)
- Resposta
-
\(96y^2-25x^2+110y+25=0\)
26)\(r(5+2\cos \theta )=6\)
27)\(r(2-\cos \theta )=1\)
- Resposta
-
\(3x^2+4y^2-2x-1=0\)
28)\(r(2.5-2.5\sin \theta )=5\)
29)\(r=\dfrac{6\sec \theta }{-2+3\sec \theta }\)
- Resposta
-
\(5x^2+9y^2-24x-36=0\)
30)\(r=\dfrac{6\csc \theta }{3+2\csc \theta }\)
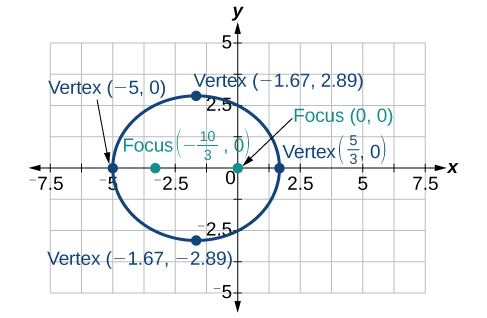
Para os exercícios 31-42, represente graficamente a seção cônica dada. Se for uma parábola, rotule o vértice, o foco e a diretriz. Se for uma elipse, rotule os vértices e os focos. Se for uma hipérbole, rotule os vértices e os focos.
31)\(r=\dfrac{5}{2+\cos \theta }\)
- Resposta
-
32)\(r=\dfrac{2}{3+3\sin \theta }\)
33)\(r=\dfrac{10}{5-4\sin \theta }\)
- Resposta
-
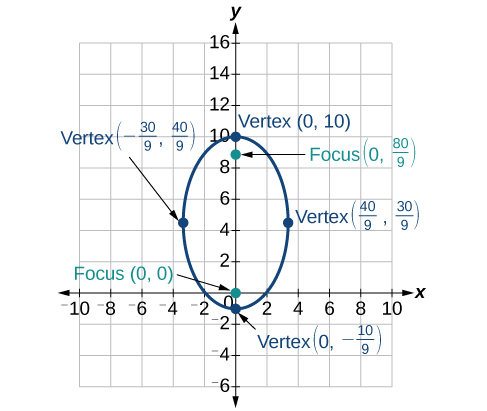
34)\(r=\dfrac{3}{1+2\cos \theta }\)
35)\(r=\dfrac{8}{4-5\cos \theta }\)
- Resposta
-
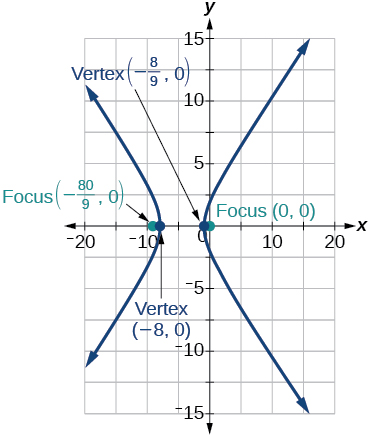
36)\(r=\dfrac{3}{4-4\cos \theta }\)
37)\(r=\dfrac{2}{1-\sin \theta }\)
- Resposta
-
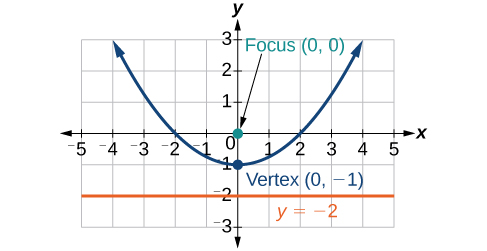
38)\(r=\dfrac{6}{3+2\sin \theta }\)
39)\(r(1+\cos \theta )=5\)
- Resposta
-
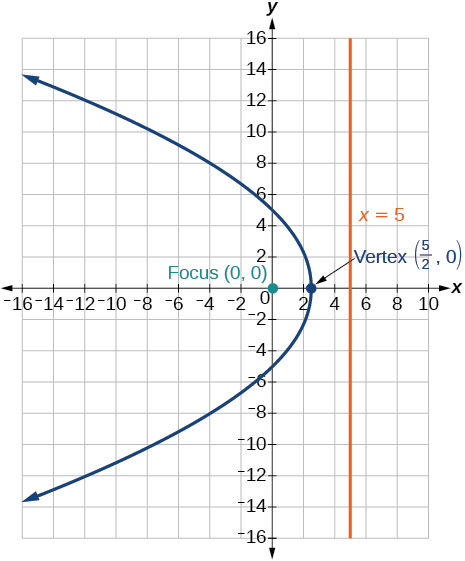
40)\(r(3-4\sin \theta )=9\)
41)\(r(3-2\sin \theta )=6\)
- Resposta
-
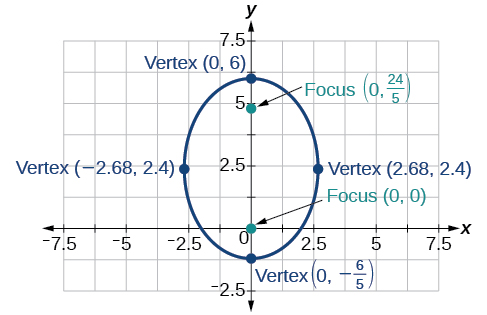
42)\(r(4-6\cos \theta )=5\)
Para os exercícios 43-, encontre a equação polar da cônica com foco na origem e a excentricidade e diretriz dadas.
43) Diretriz:\(x=4\);\(e=\dfrac{1}{5}\)
- Resposta
-
\(r=\dfrac{4}{5+\cos \theta }\)
4) Diretriz:\(x=-4\)\(e=5\)
45) Diretriz:\(y=2\);\(e=2\)
- Resposta
-
\(r=\dfrac{4}{1+2\sin \theta }\)
46) Diretriz:\(y=-2\);\(e=\dfrac{1}{2}\)
47) Diretriz:\(x=1\)\(e=1\)
- Resposta
-
\(r=\dfrac{1}{1+\cos \theta }\)
48) Diretriz:\(x=-1\);\(e=1\)
49) Diretriz:\(x=-\dfrac{1}{4}\);\(e=\dfrac{7}{2}\)
- Resposta
-
\(r=\dfrac{7}{8-28\cos \theta }\)
50) Diretriz:\(y=-\dfrac{2}{5}\);\(e=\dfrac{7}{2}\)
51) Diretriz:\(y=4\);\(e=\dfrac{3}{2}\)
- Resposta
-
\(r=\dfrac{12}{2+3\sin \theta }\)
52) Diretriz:\(x=-2\);\(e=\dfrac{8}{3}\)
53) Diretriz:\(x=-5\);\(e=\dfrac{3}{4}\)
- Resposta
-
\(r=\dfrac{15}{4-3\cos \theta }\)
54) Diretriz:\(y=2\);\(e=2.5\)
5) Diretriz:\(x=-3\)\(e=\dfrac{1}{3}\)
- Resposta
-
\(r=\dfrac{3}{3-3\cos \theta }\)
Extensões
Lembre-se de Rotation of Axes que equações de cônicas com um\(xy\) termo têm gráficos girados. Para os exercícios a seguir, expresse cada equação na forma polar com\(r\) em função de\(\theta \).
56)\(xy=2\)
57)\(x^2+xy+y^2=4\)
- Resposta
-
\(r=\pm \dfrac{2}{\sqrt{1+\sin \theta \cos \theta }}\)
58)\(2x^2+4xy+2y^2=9\)
59)\(16x^2+24xy+9y^2=4\)
- Resposta
-
\(r=\pm \dfrac{2}{4\cos \theta +3\sin \theta }\)
60)\(2xy+y=1\)


