10.R: Geometria Analítica (Revisão)

10.1: A elipse

Nesta seção, investigaremos a forma desta sala e suas aplicações no mundo real, incluindo a distância entre duas pessoas no Statuary Hall e ainda ouvirem uma à outra sussurrar.

Para os exercícios 1-4, escreva a equação da elipse na forma padrão. Em seguida, identifique o centro, os vértices e os focos.

1)$\dfrac{x^2}{25}+\dfrac{y^2}{64}=1$

Responda

$\dfrac{x^2}{5^2}+\dfrac{y^2}{8^2}=1$; centro:$(0,0)$; Vértices:$(5,0)$$(-5,0)$,$(0,8)$,,$(0,-8)$; focos:$(0,\sqrt{39})$,$(0,-\sqrt{39})$

2)$\dfrac{(x-2)^2}{100}+\dfrac{(y+3)^2}{36}=1$

3)$9x^2+y^2+54x-4y+76=0$

Responda

$\dfrac{(x+3)^2}{1^2}+\dfrac{(y-2)^2}{3^2}=1$; centro:$(-3,2)$; Vértices:$(-2,2)$$(-4,2)$,$(-3,5)$,,$(-3,-1)$; focos:$(-3,2+2\sqrt{2})$,$(-3,2-2\sqrt{2})$

4)$9x^2+36y^2-36x+72y+36=0$

Para os exercícios 5-8, faça um gráfico da elipse, observando o centro, os vértices e os focos.

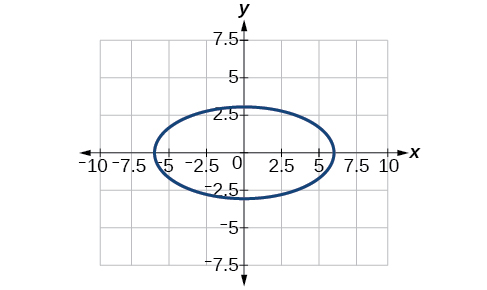
5)$\dfrac{x^2}{36}+\dfrac{y^2}{9}=1$

Responda

centro:$(0,0)$; Vértices:$(6,0$$(-6,0)$,$(0,3)$,,$(0,-3)$; focos:$(3\sqrt{3},0)$,$(-3\sqrt{3},0)$

6)$\dfrac{(x-4)^2}{25}+\dfrac{(y+3)^2}{49}=1$

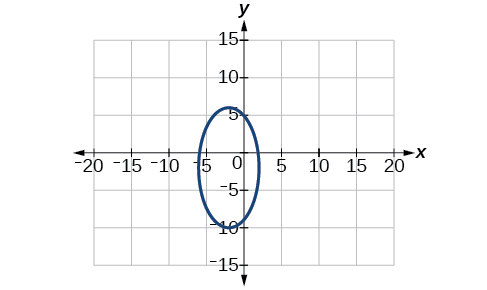
7)$4x^2+y^2+16x+4y-44=0$

Responda

centro:$(-2,-2)$; Vértices:$(2,-2)$$(-6,-2)$,$(-2,6)$,,$(-2,-10)$; focos:$(-2,-2+4\sqrt{3})$,$(-2,-2-4\sqrt{3})$

8)$2x^2+3y^2-20x+12y+38=0$

Para os exercícios 9-11, use as informações fornecidas para encontrar a equação da elipse.

9) Centro em$(0,0)$, foco em$(3,0)$, vértice em$(-5,0)$

Responda

$\dfrac{x^2}{25}+\dfrac{y^2}{16}=1$

10) Centro em$(2,-2)$, vértice em$(7,-2)$, foco em$(4,-2)$

11) Uma galeria sussurrante deve ser construída de forma que os focos estejam localizados a$35$ poucos metros do centro. Se o comprimento da galeria for de$100$ pés, qual deve ser a altura do teto?

Responda

Aproximadamente$35.71$ pés

10.2: A hipérbole

Em geometria analítica, uma hipérbole é uma seção cônica formada pela interseção de um cone circular reto com um plano em um ângulo de forma que ambas as metades do cone sejam cruzadas. Essa interseção produz duas curvas separadas e ilimitadas que são imagens espelhadas uma da outra.

Para os exercícios 1-4, escreva a equação da hipérbole na forma padrão. Em seguida, forneça o centro, os vértices e os focos.

1)$\dfrac{x^2}{81}-\dfrac{y^2}{9}=1$

2)$\dfrac{(y+1)^2}{16}-\dfrac{(x-4)^2}{36}=1$

Responda

$\dfrac{(y+1)^2}{4^2}-\dfrac{(x-4)^2}{6^2}=1$; centro:$(4,-1)$; Vértices:$(4,3)$,$(4,-5)$; focos:$(4,-1+2\sqrt{13})$,$(4,-1-2\sqrt{13})$

3)$9y^2-4x^2+54y-16x+29=0$

4)$3x^2-y^2-12x-6y-9=0$

Responda

$\dfrac{(x-2)^2}{2^2}-\dfrac{(y+3)^2}{(2\sqrt{3})^2}=1$; centro:$(2,-3)$; Vértices:$(4,-3)$,$(0,-3)$; focos:$(6,-3)$,$(-2,-3)$

Para os exercícios 5-8, faça um gráfico da hipérbole, rotulando vértices e focos.

5)$\dfrac{x^2}{9}-\dfrac{y^2}{16}=1$

6)$\dfrac{(y-1)^2}{49}-\dfrac{(x+1)^2}{4}=1$

Responda

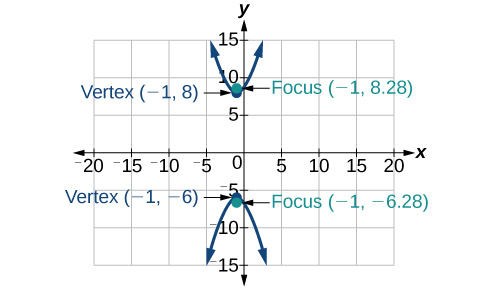
7)$x^2-4y^2+6x+32y-91=0$

8)$2y^2-x^2-12y-6=0$

Responda

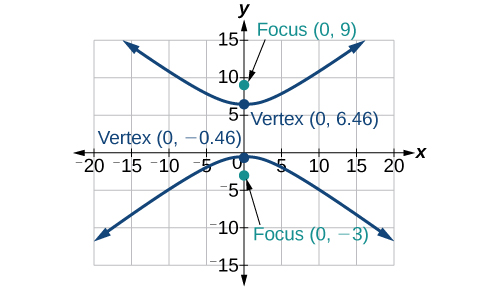
Para os exercícios 9-10, encontre a equação da hipérbole.

9) Centro em$(0,0)$, vértice em$(0,4)$, foco em$(0,-6)$

10) Focos em$(3,7)$ e$(7,7)$, vértice em$(6,7$

Responda

$\dfrac{(x-5)^2}{1}-\dfrac{(y-7)^2}{3}=1$

10.3: A parábola

Como a elipse e a hipérbole, a parábola também pode ser definida por um conjunto de pontos no plano coordenado. Uma parábola é o conjunto de todos os pontos em um plano que estão à mesma distância de uma linha fixa, chamada diretriz, e um ponto fixo (o foco) que não está na diretriz.

Para os exercícios 1-4, escreva a equação da parábola na forma padrão. Em seguida, dê o vértice, o foco e a diretriz.

1)$y^2=12x$

2)$(x+2)^2=\dfrac{1}{2}(y-1)$

Responda

$(x+2)^2=\dfrac{1}{2}(y-1)$; vértice:$(-2,1)$; foco:$\left( -2, \dfrac{9}{8} \right )$; diretriz:$y=\dfrac{7}{8}$

3)$y^2-6y-6x-3=0$

4)$x^2+10x-y+23=0$

Responda

$(x+5)^2=(y+2)$; vértice:$(-5,-2)$; foco:$\left( -5, -\dfrac{7}{4} \right )$; diretriz:$y=-\dfrac{9}{4}$

Para os exercícios 5-8, represente graficamente a parábola, rotulando vértice, foco e diretriz.

5)$x^2+4y=0$

6)$(y-1)^2=\dfrac{1}{2}(x+3)$

Responda

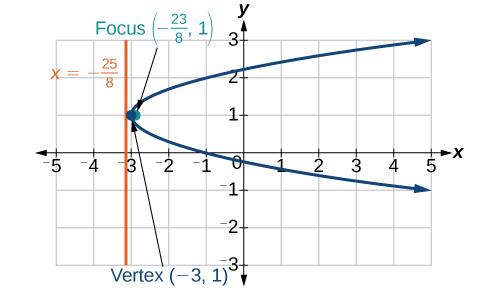
7)$x^2-8x-10y+46=0$

8)$2y^2+12y+6x+15=0$

Responda

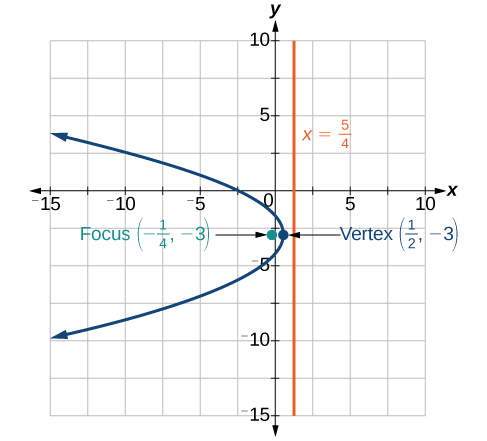
Para os exercícios 9-11, escreva a equação da parábola usando as informações fornecidas.

9) Concentre-se em$(-4,0)$; a diretriz é$x=4$

10) Concentre-se em$\left( 2, \dfrac{9}{8} \right )$; a diretriz é$y=\dfrac{7}{8}$

Responda

$(x-2)^2= \left (\dfrac{1}{2} \right ) (y-1)$

11) Uma antena receptora de TV a cabo tem a forma de um parabolóide da revolução. Encontre a localização do receptor, que é colocado no foco, se o prato tiver$5$ pés de diâmetro na abertura e$1.5$ pés de profundidade.

10.4: Rotação dos eixos

Nas seções anteriores deste capítulo, nos concentramos nas equações de forma padrão para seções cônicas não degeneradas. Nesta seção, vamos mudar nosso foco para a equação geral da forma, que pode ser usada para qualquer cônica. A forma geral é definida como igual a zero, e os termos e coeficientes são fornecidos em uma ordem específica, conforme mostrado abaixo.

Para os exercícios 1-3, determine qual das seções cônicas está representada.

1)$16x^2+24xy+9y^2+24x-60y-60=0$

Responda

$B^2 - 4AC =0$, parábola

2)$4x^2+14xy+5y^2+18x-6y+30=0$

3)$4x^2+xy+2y^2+8x-26y+9=0$

Responda

$B^2 - 4AC = -31 < 0$, elipse

Para os exercícios 4-5, determine o ângulo$\theta$ que eliminará o$xy$ termo e escreva a equação correspondente sem o$xy$ termo.

4)$x^2+4xy-2y^2-6=0$

5)$x^2-xy+y^2-6=0$

Responda

$\theta =45^{\circ},x'^2+3y'^2-12=0$

Para os exercícios 6-8, represente graficamente a equação em relação ao$x'y'$ sistema no qual a equação não tem$x'y'$ termo.

6)$9x^2-24xy+16y^2-80x-60y+100=0$

7)$x^2-xy+y^2-2=0$

Responda

$\theta =45^{\circ}$

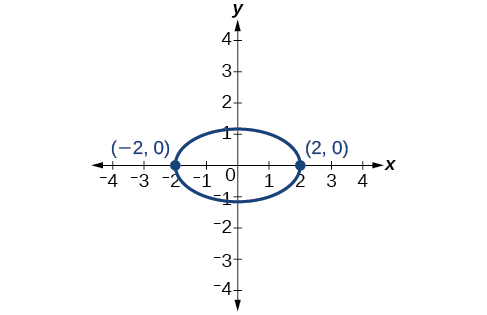
8)$6x^2+24xy-y^2-12x+26y+11=0$

10.5: Seções cônicas em coordenadas polares

Nesta seção, aprenderemos como definir qualquer cônica no sistema de coordenadas polares em termos de um ponto fixo, o foco no polo e uma linha, a diretriz, que é perpendicular ao eixo polar.

Para os exercícios 1-4, dada a equação polar da cônica com foco na origem, identifique a excentricidade e a diretriz.

1)$r=\dfrac{10}{1-5\cos \theta }$

Responda

Hipérbole com$e=5$$2$ unidades diretivas à esquerda do poste.

2)$r=\dfrac{6}{3+2\cos \theta }$

3)$r=\dfrac{1}{4+3\sin \theta }$

Responda

Elipse com$e=\dfrac{3}{4}$ uma$\dfrac{1}{3}$ unidade diretriz acima do polo.

4)$r=\dfrac{3}{5-5\sin \theta }$

Para os exercícios 5-8, represente graficamente a cônica dada na forma polar. Se for uma parábola, rotule o vértice, o foco e a diretriz. Se for uma elipse ou uma hipérbole, rotule os vértices e focos.

5)$r=\dfrac{3}{1-\sin \theta }$

Responda

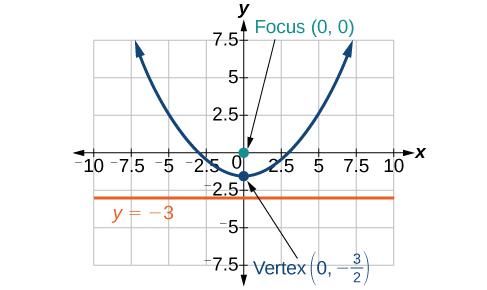
6)$r=\dfrac{8}{4+3\sin \theta }$

7)$r=\dfrac{10}{4+5\cos \theta }$

Responda

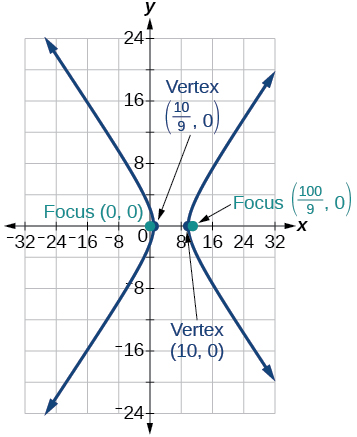
8)$r=\dfrac{9}{3-6\cos \theta }$

Para os exercícios 9-10, dadas as informações sobre o gráfico de uma cônica com foco na origem, encontre a equação na forma polar.

9) Directrix é uma$x=3$ excentricidade$e=1$

Responda

$r=\dfrac{3}{1+\cos \theta }$

10) Directrix é uma$y=-2$ excentricidade$e=4$

Teste prático

Para os exercícios 1-2, escreva a equação na forma padrão e indique o centro, os vértices e os focos.

1)$\dfrac{x^2}{9}+\dfrac{y^2}{4}=1$

Responda

$\dfrac{x^2}{3^2}+\dfrac{y^2}{2^2}=1$; centro:$(0,0)$; vértices:$(3,0)$,$(-3,0)$,$(0,2)$,$(0,-2)$; focos:$(\sqrt{5},0)$,$(-\sqrt{5},0)$

2)$9y^2+16x^2-36y+32x-92=0$

Para os exercícios 3-6, esboce o gráfico, identificando o centro, os vértices e os focos.

3)$\dfrac{(x-3)^2}{64}+\dfrac{(y-2)^2}{36}=1$

Responda

centro:$(3,2)$; vértices:$(11,2)$,$(-5,2)$,$(3,8)$,$(3,-4)$; focos:$(3+2\sqrt{7},2)$,$(3-2\sqrt{7},2)$

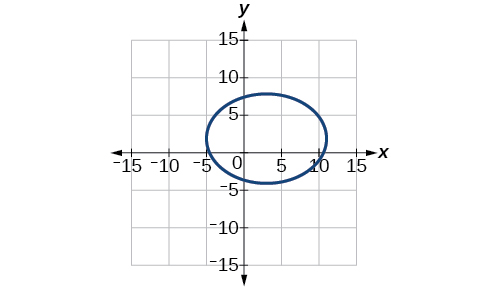
4)$2x^2+y^2+8x-6y-7=0$

5) Escreva a equação da forma padrão de uma elipse com centro em$(1,2)$, vértice em$(7,2)$ e foco em$(4,2)$.

Responda

$\dfrac{(x-1)^2}{36}+\dfrac{(y-2)^2}{27}=1$

6) Uma galeria sussurrante deve ser construída com um comprimento de$150$ pés. Se os focos estiverem localizados a poucos$20$ metros da parede, qual deve ser a altura do teto?

Para os exercícios 7-8, escreva a equação da hipérbole na forma padrão e forneça o centro, os vértices, os focos e as assíntotas.

7)$\dfrac{x^2}{49}-\dfrac{y^2}{81}=1$

Responda

$\dfrac{x^2}{7^2}-\dfrac{y^2}{9^2}=1$; centro:$(0,0)$; vértices:$(7,0)$,$(-7,0)$; focos:$(\sqrt{130},0)$,$(-\sqrt{130},0)$; assíntotas:$y=\pm \dfrac{9}{7}x$

8)$16y^2-9x^2+128y+112=0$

Para os exercícios 9-11, faça um gráfico da hipérbole, observando seu centro, vértices e focos. Indique as equações das assíntotas.

9)$\dfrac{(x-3)^2}{25}-\dfrac{(y+3)^2}{1}=1$

Responda

centro:$(3,-3)$; vértices:$(8,-3)$,$(-2,-3)$; focos:$(3+\sqrt{26},-3)$,$(3-\sqrt{26},-3)$; assíntotas:$y=\pm \dfrac{1}{5}(x-3)-3$

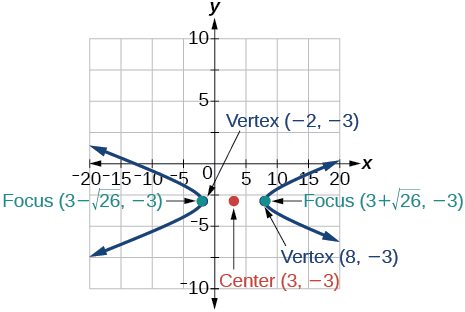
10)$y^2-x^2+4y-4x-18=0$

11) Escreva a equação da forma padrão de uma hipérbole com focos em$(1,0)$$(1,6)$, e e um vértice em$(1,2)$.

Responda

$\dfrac{(y-3)^2}{1}-\dfrac{(x-1)^2}{8}=1$

Para os exercícios 12-13, escreva a equação da parábola na forma padrão e forneça o vértice, o foco e a equação da diretriz.

12)$y^2+10x=0$

13)$3x^2-12x-y+11=0$

Responda

$(x-2)^2=\dfrac{1}{3}(y+1)$; vértice:$(2,-1)$; foco:$(2,-\dfrac{11}{12})$; diretriz:$y=-\dfrac{13}{12}$

Para os exercícios 14-17, faça um gráfico da parábola, rotulando o vértice, o foco e a diretriz.

14)$(x-1)^2=-4(y+3)$

15)$y^2+8x-8y+40=0$

Responda

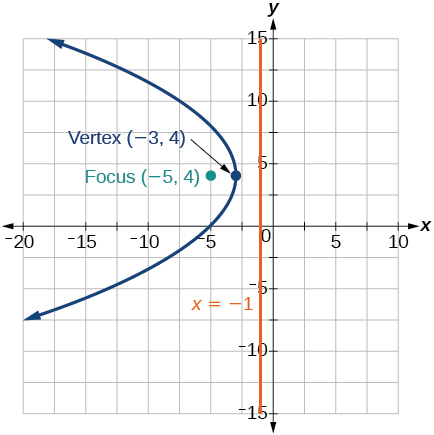
16) Escreva a equação de uma parábola com foco em$(2,3)$ e diretriz$y=-1$.

17) Um holofote tem a forma de um parabolóide da revolução. Se a fonte de luz estiver localizada a$1.5$ pés da base ao longo do eixo de simetria e a profundidade do holofote for$3$ pés, qual deve ser a largura da abertura?

Responda

Aproximadamente$8.49$ pés

Para os exercícios 18-19, determine qual seção cônica é representada pela equação dada e, em seguida, determine o ângulo$\theta$ que eliminará o$xy$ termo.

18)$3x^2-2xy+3y^2=4$

19)$x^2+4xy+4y^2+6x-8y=0$

Responda

parábola;$\theta \approx 63.4^{\circ}$

Para os exercícios 20-21, reescreva no$x'y'$ sistema sem o$x'y'$ termo e faça um gráfico do gráfico girado.

20)$11x^2+10\sqrt{3}xy+y^2=4$

21)$16x^2+24xy+9y^2-125x=0$

Responda

$x'^2-4x'+3y'=0$

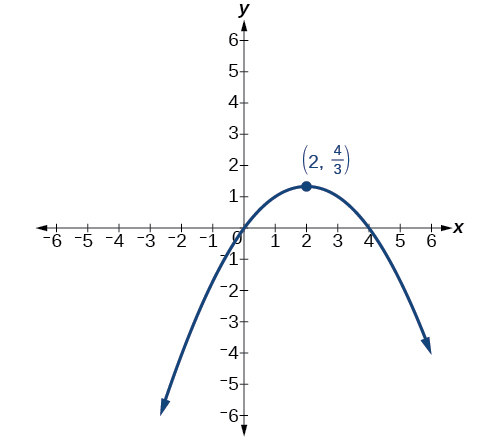
Para os exercícios 22-23, identifique a cônica com foco na origem e, em seguida, forneça a diretriz e a excentricidade.

22)$r=\dfrac{3}{2-\sin \theta }$

23)$r=\dfrac{5}{4+6\cos \theta }$

Responda

Hipérbole com$e=\dfrac{3}{2}$$\dfrac{5}{6}$ unidades diretivas à direita do poste.

Para os exercícios 24-26, represente graficamente a seção cônica dada. Se for uma parábola, rotule vértice, foco e diretriz. Se for uma elipse ou uma hipérbole, rotule vértices e focos.

24)$r=\dfrac{12}{4-8\sin \theta }$

25)$r=\dfrac{2}{4+4\sin \theta }$

Responda

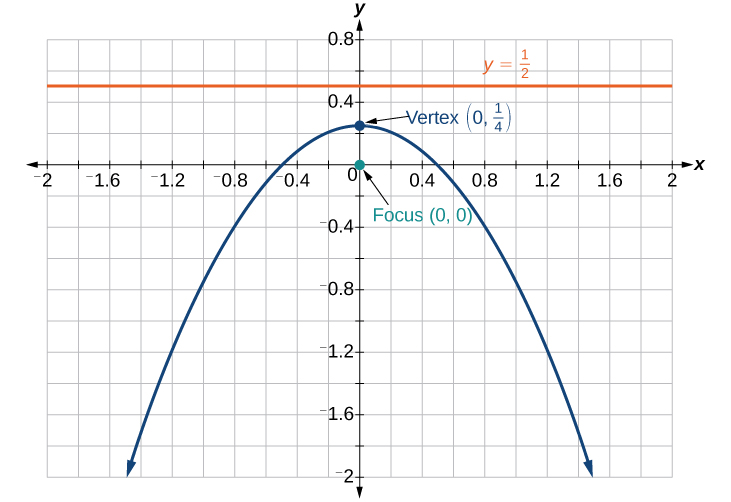
26) Encontre uma equação polar da cônica com foco na origem, excentricidade e diretriz:$x=3$.$e=2$

Contribuidores e atribuições

• Template:OpenStaxPreCalc