9.8: Resolvendo sistemas com a regra de Cramer
- Page ID
- 189124
- Avalie os determinantes 2 × 2.
- Use a Regra de Cramer para resolver um sistema de equações em duas variáveis.
- Avalie 3 × 3 determinantes.
- Use a Regra de Cramer para resolver um sistema de três equações em três variáveis.
- Conheça as propriedades dos determinantes.
Aprendemos como resolver sistemas de equações em duas variáveis e três variáveis e por vários métodos: substituição, adição, eliminação gaussiana, usando o inverso de uma matriz e representação gráfica. Alguns desses métodos são mais fáceis de aplicar do que outros e são mais apropriados em determinadas situações. Nesta seção, estudaremos mais duas estratégias para resolver sistemas de equações.
Avaliando o determinante de uma matriz 2 × 2
Um determinante é um número real que pode ser muito útil em matemática porque tem várias aplicações, como calcular área, volume e outras quantidades. Aqui, usaremos determinantes para revelar se uma matriz é invertível usando as entradas de uma matriz quadrada para determinar se há uma solução para o sistema de equações. Talvez uma das aplicações mais interessantes, no entanto, seja seu uso em criptografia. Às vezes, sinais ou mensagens seguros são enviados codificados em uma matriz. Os dados só podem ser decifrados com uma matriz invertível e o determinante. Para nossos propósitos, focamos no determinante como uma indicação da invertibilidade da matriz. O cálculo do determinante de uma matriz envolve seguir os padrões específicos descritos nesta seção.
O determinante de uma matriz 2 × 2, dado
\(A=\begin{bmatrix}a&b\\c&d\end{bmatrix}\)
é definido como

Observe a mudança na notação. Existem várias maneiras de indicar o determinante, incluindo\(\det(A)\) e substituindo os colchetes em uma matriz por linhas retas\(| A |\).
Encontre o determinante da matriz dada.
\(A=\begin{bmatrix}5&2\\−6&3\end{bmatrix}\)
Solução
\[\begin{align*} \det(A)&= \begin{vmatrix}5&2\\-6&3\end{vmatrix}\\ &= 5(3)-(-6)(2)\\ &= 27 \end{align*}\]
Usando a regra de Cramer para resolver um sistema de duas equações em duas variáveis
Agora, apresentaremos um método final para resolver sistemas de equações que usam determinantes. Conhecida como Regra de Cramer, essa técnica remonta a meados do século XVIII e recebeu o nome de seu inovador, o matemático suíço Gabriel Cramer (1704-1752), que a introduziu em 1750 na Introduction à l'Analyse des lignes Courbes algébriques. A Regra de Cramer é um método viável e eficiente para encontrar soluções para sistemas com um número arbitrário de incógnitas, desde que tenhamos o mesmo número de equações que as incógnitas.
A Regra de Cramer nos dará a solução única para um sistema de equações, se ele existir. No entanto, se o sistema não tiver solução ou um número infinito de soluções, isso será indicado por um determinante de zero. Para descobrir se o sistema é inconsistente ou dependente, outro método, como a eliminação, deverá ser usado.
Para entender a Regra de Cramer, vamos examinar mais de perto como resolvemos sistemas de equações lineares usando operações básicas de linha. Considere um sistema de duas equações em duas variáveis.
\[\begin{align} a_1x+b_1y&= c_1 (1) \label{eq1}\\ a_2x+b_2y&= c_2 (2) \label{eq2}\\ \end{align}\]
Eliminamos uma variável usando operações de linha e resolvemos pela outra. Digamos que desejamos resolver\(x\). Se a Equação\ ref {eq2} for multiplicada pelo oposto do coeficiente de\(y\) na Equação\ ref {eq1}, a Equação\ ref {eq1} for multiplicada pelo coeficiente de\(y\) na Equação\ ref {eq2}, e adicionarmos as duas equações, a variável\(y\) será eliminada.
\[\begin{align*} &b_2a_1x+b_2b_1y = b_2c_1 & \text{Multiply }R_1 \text{ by }b_2 \\ -&\underline{b_1a_2x−b_1b_2y=−b_1c_2} & \text{Multiply }R_2 \text{ by }−b_1 \\ & b_2a_1x−b_1a_2x=b_2c_1−b_1c_2 \end{align*}\]
Agora, resolva\(x\).
\[\begin{align*} b_2a_1x−b_1a_2x &= b_2c_1−b_1c_2 \\ x(b_2a_1−b_1a_2) &= b_2c_1−b_1c_2 \\ x &= \dfrac{b_2c_1−b_1c_2}{b_2a_1−b_1a_2}=\dfrac{\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}} \end{align*}\]
Da mesma forma, para resolver\(y\), eliminaremos\(x\).
\[\begin{align*} & a_2a_1x+a_2b_1y = a_2c_1 & \text{Multiply }R_1 \text{ by }a_2 \\ -& \underline{a_1a_2x−a_1b_2y=−a_1c_2} & \text{Multiply }R_2 \text{ by }−a_1 \\ & a_2b_1y−a_1b_2y =a_2c_1−a_1c_2 \end{align*}\]
Resolvendo\(y\) doações
\[ \begin{align*} a_2b_1y−a_1b_2y &= a_2c_1−a_1c_2 \\ y(a_2b_1−a_1b_2) &= a_2c_1−a_1c_2 \\ y &= \dfrac{a_2c_1−a_1c_2}{a_2b_1−a_1b_2}=\dfrac{a_1c_2−a_2c_1}{a_1b_2−a_2b_1}=\dfrac{\begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}} \end{align*}\]
Observe que o denominador para ambos\(x\) e\(y\) é o determinante da matriz de coeficientes.
Podemos usar essas fórmulas para resolver\(x\) e\(y\), mas a Regra de Cramer também introduz uma nova notação:
- \(D\):determinante da matriz de coeficientes
- \(D_x\):determinante do numerador na solução de\(x\)
\[x=\dfrac{D_x}{D}\]
- \(D_y\):determinante do numerador na solução de\(y\)
\[y=\dfrac{D_y}{D}\]
A chave para a Regra de Cramer é substituir a coluna variável de interesse pela coluna constante e calcular os determinantes. Podemos então expressar\(x\) e\(y\) como um quociente de dois determinantes.
A Regra de Cramer é um método que usa determinantes para resolver sistemas de equações que têm o mesmo número de equações das variáveis.
Considere um sistema de duas equações lineares em duas variáveis.
\[\begin{align*} a_1x+b_1y&= c_1\\ a_2x+b_2y&= c_2 \end{align*}\]
A solução usando a Regra de Cramer é dada como
\[\begin{align} x&= \dfrac{D_x}{D} = \dfrac{\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}}\; , D\neq 0\\ y&= \dfrac{D_y}{D} = \dfrac{\begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}}\; , D\neq 0 \end{align}\]
Se estivermos resolvendo\(x\), a\(x\) coluna será substituída pela coluna constante. Se estivermos resolvendo\(y\), a\(y\) coluna será substituída pela coluna constante.
Resolva o seguinte\(2 × 2\) sistema usando a Regra de Cramer.
\[\begin{align*} 12x+3y&= 15\\ 2x-3y&= 13 \end{align*}\]
Solução
Resolver para\(x\).
\[\begin{align*} x&= \dfrac{D_x}{D}\\ &= \dfrac{\begin{bmatrix}15&3\\13&-3\end{bmatrix}}{\begin{bmatrix}12&3\\2&-3\end{bmatrix}}\\ &= \dfrac{-45-39}{-36-6}\\ &= \dfrac{-84}{-42}\\ &= 2 \end{align*}\]
Resolver para\(y\).
\[\begin{align*} y&= \dfrac{D_y}{D}\\ &= \dfrac{\begin{bmatrix}12&15\\2&13\end{bmatrix}}{\begin{bmatrix}12&3\\2&-3\end{bmatrix}}\\ &= \dfrac{156-30}{-36-6}\\ &= -\dfrac{126}{42}\\ &= -3 \end{align*}\]
A solução é\((2,−3)\).
Use a Regra de Cramer para resolver o\(2 × 2\) sistema de equações.
\[\begin{align*} x+2y&= -11\\ -2x+y&= -13 \end{align*}\]
- Responda
-
\((3,−7)\)
Avaliando o determinante de uma matriz 3 × 3
Encontrar o determinante de uma matriz 2×2 é simples, mas encontrar o determinante de uma matriz 3×3 é mais complicado. Um método é aumentar a matriz 3 × 3 com uma repetição das duas primeiras colunas, dando uma matriz 3 × 5. Em seguida, calculamos a soma dos produtos das entradas abaixo de cada uma das três diagonais (superior esquerda para inferior direita) e subtraímos os produtos das entradas em cada uma das três diagonais (inferior esquerda para superior direita). Isso é mais facilmente entendido com um visual e um exemplo.
Encontre o determinante da matriz 3×3.
\(A=\begin{bmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{bmatrix}\)
- Aumente\(A\) com as duas primeiras colunas.
\(\det(A)=\left| \begin{array}{ccc|cc} a_1&b_1&c_1&a_1&b_1\\a_2&b_2&c_2&a_2&b_2\\a_3&b_3&c_3&a_3&b_3\end{array} \right|\)
- Do canto superior esquerdo para o canto inferior direito: multiplique as entradas pela primeira diagonal. Adicione o resultado ao produto das entradas abaixo da segunda diagonal. Adicione esse resultado ao produto das entradas abaixo da terceira diagonal.
- Do canto inferior esquerdo para o canto superior direito: subtraia o produto das entradas acima da primeira diagonal. A partir desse resultado, subtraia o produto das entradas até a segunda diagonal. A partir desse resultado, subtraia o produto das entradas até a terceira diagonal.
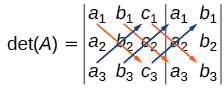
A álgebra é a seguinte:
\(| A |=a_1b_2c_3+b_1c_2a_3+c_1a_2b_3−a_3b_2c_1−b_3c_2a_1−c_3a_2b_1\)
Encontre o determinante da\(3 × 3\) matriz dada
\(A=\begin{bmatrix}0&2&1\\3&−1&1\\4&0&1\end{bmatrix}\)
Solução
Aumente a matriz com as duas primeiras colunas e siga a fórmula. Assim,
\[\begin{align*} | A | &= \left| \begin{array}{ccc|cc}0&2&1&0&2\\3&-1&1&3&-1\\4&0&1&4&0\end{array}\right| \\ &= 0(−1)(1)+2(1)(4)+1(3)(0)−4(−1)(1)−0(1)(0)−1(3)(2) \\ &=0+8+0+4−0−6 \\ &= 6 \end{align*}\]
Encontre o determinante da matriz 3 × 3.
\(\det(A)=\begin{vmatrix}1&−3&7\\1&1&1\\1&−2&3\end{vmatrix}\)
- Responda
-
\(−10\)
Não, esse método funciona apenas para matrizes 2 × 2 e 3 × 3. Para matrizes maiores, é melhor usar um utilitário gráfico ou software de computador.
Usando a regra de Cramer para resolver um sistema de três equações em três variáveis
Agora que podemos encontrar o determinante de uma\(3 × 3\) matriz, podemos aplicar a Regra de Cramer para resolver um sistema de três equações em três variáveis. A Regra de Cramer é simples, seguindo um padrão consistente com a Regra de Cramer para\(2 × 2\) matrizes. À medida que a ordem da matriz aumenta para\(3 × 3\), no entanto, são necessários muitos outros cálculos.
Quando calculamos o determinante como zero, a Regra de Cramer não indica se o sistema não tem solução ou um número infinito de soluções. Para descobrir, temos que realizar a eliminação no sistema.
Considere um\(3 × 3\) sistema de equações.
\[\begin{align} a_1x+b_1y+c_1z &= \color{blue}d_1 \\ a_2x+b_2y+c_2z &= \color{blue}d_2 \\ a_3x+b_3y+c_3z &= \color{blue}d_3 \\ \end{align}\]
\(x=\dfrac{D_x}{D}\),\(y=\dfrac{D_y}{D}\),\(z=\dfrac{D_z}{D}\),\(D≠0\)
onde
\[D = \begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix}\; ,\; D_x = \begin{vmatrix} \color{blue}d_1 & b_1 & c_1\\ \color{blue}d_2 & b_2 & c_2\\ \color{blue}d_3 & b_3 & c_3 \end{vmatrix}\; ,\; D_y = \begin{vmatrix} a_1 & \color{blue}d_1 & c_1\\ a_2 & \color{blue}d_2 & c_2\\ a_3 & \color{blue}d_3 & c_3 \end{vmatrix}\; ,\; D_z = \begin{vmatrix} a_1 & b_1 & \color{blue}d_1\\ a_2 & b_2 & \color{blue}d_2\\ a_3 & b_3 & \color{blue}d_3 \end{vmatrix}\]
Se estivermos escrevendo o determinante\(D_x\), substituímos a\(x\) coluna pela coluna constante. Se estivermos escrevendo o determinante\(D_y\), substituímos a coluna y pela coluna constante. Se estivermos escrevendo o determinante\(D_z\), substituímos a\(z\) coluna pela coluna constante. Sempre verifique a resposta.
Encontre a solução para o\(3 × 3\) sistema fornecido usando a Regra de Cramer.
\[\begin{align*} x+y-z&= 6\\ 3x-2y+z&= -5\\ x+3y-2z&= 14 \end{align*}\]
Solução
Use a regra de Cramer.
\(D=\begin{vmatrix}1&1&−1\\3&−2&1\\1&3&−2\end{vmatrix}\),\(D_x=\begin{vmatrix}6&1&−1\\−5&−2&1\\14&3&−2\end{vmatrix}\),\(D_y=\begin{vmatrix}1&6&−1\\3&−5&1\\1&14&−2\end{vmatrix}\),\(D_z=\begin{vmatrix}1&1&6\\3&−2&−5\\1&3&14\end{vmatrix}\)
Em seguida,
\[\begin{align*} x&= \dfrac{D_x}{D}&= \dfrac{-3}{-3}&= 1\\ y&= \dfrac{D_y}{D}&= \dfrac{-9}{-3}&= 3\\ z&= \dfrac{D_z}{D}&= \dfrac{6}{-3}&= -2\\ \end{align*}\]
A solução é\((1,3,−2)\).
Use a Regra de Cramer para resolver a\(3 × 3\) matriz.
\[\begin{align*} x-3y+7z&= 13\\ x+y+z&= 1\\ x-2y+3z&= 4 \end{align*}\]
- Responda
-
\(\left(−2,\dfrac{3}{5},\dfrac{12}{5}\right)\)
Resolva o sistema de equações usando a Regra de Cramer.
\[\begin{align} 3x-2y&= 4 \label{eq3}\\ 6x-4y&= 0 \label{eq4}\end{align}\]
Solução
Começamos encontrando os determinantes\(D\)\(D_x\),\(D_y\) e.
\(D=\begin{vmatrix}3&−2\\6&−4\end{vmatrix}=3(−4)−6(−2)=0\)
Sabemos que um determinante de zero significa que ou o sistema não tem solução ou tem um número infinito de soluções. Para ver qual deles, usamos o processo de eliminação. Nosso objetivo é eliminar uma das variáveis.
- Multiplique a equação\ ref {eq3} por\(−2\).
- Adicione o resultado à Equação\ ref {eq4}.
\[\begin{align*} &−6x+4y=−8 \\ &\;\;\;\underline{6x−4y=0} \\ &\;\;\;\;\;\;\;\;\;\; 0=−8 \end{align*}\]
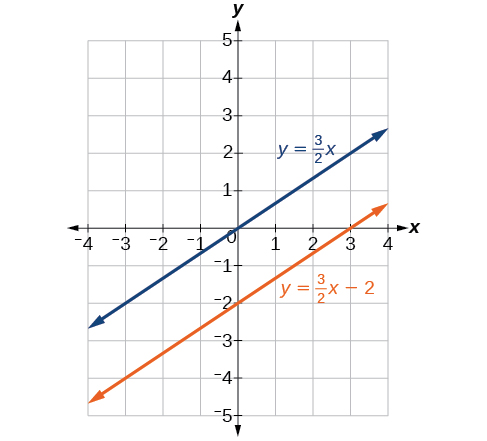
Obtemos a equação\(0=−8\), que é falsa. Portanto, o sistema não tem solução. A representação gráfica do sistema revela duas linhas paralelas. Veja a Figura\(\PageIndex{1}\).
Resolva o sistema com um número infinito de soluções.
\[\begin{align} x-2y+3z&= 0 \label{eq5}\\ 3x+y-2z&= 0 \label{eq6}\\ 2x-4y+6z&= 0 \label{eq7} \end{align}\]
Solução
Vamos encontrar primeiro o determinante. Configure uma matriz aumentada pelas duas primeiras colunas.
\(\left| \begin{array}{ccc|cc}1&−2&3&1&-2\\3&1&−2&3&1\\2&−4&6&2&-4\end{array}\right|\)
Em seguida,
\(1(1)(6)+(−2)(−2)(2)+3(3)(−4)−2(1)(3)−(−4)(−2)(1)−6(3)(−2)=0\)
Como o determinante é igual a zero, não há solução ou um número infinito de soluções. Temos que realizar a eliminação para descobrir.
1. Multiplique a Equação\ ref {eq5} por\(−2\) e adicione o resultado à Equação\ ref {eq7}:
\[\begin{align*} &−2x+4y−6x=0 \\ &\;\;\underline{2x−4y+6z=0} \\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0=0 \end{align*}\]
2. Obter uma resposta de\(0=0\), uma afirmação que é sempre verdadeira, significa que o sistema tem um número infinito de soluções. Representando graficamente o sistema, podemos ver que dois dos planos são iguais e ambos cruzam o terceiro plano em uma linha. Veja a Figura\(\PageIndex{2}\).
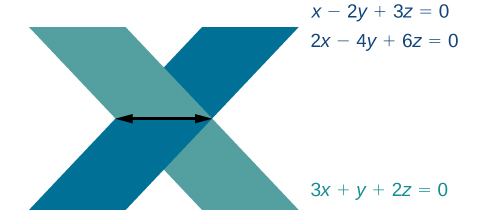
Entendendo as propriedades dos determinantes
Existem muitas propriedades dos determinantes. Aqui estão listadas algumas propriedades que podem ser úteis no cálculo do determinante de uma matriz.
- Se a matriz estiver na forma triangular superior, o determinante é igual ao produto das entradas abaixo da diagonal principal.
- Quando duas linhas são trocadas, o sinal de mudança determinante.
- Se duas linhas ou duas colunas forem idênticas, o determinante será igual a zero.
- Se uma matriz contiver uma linha de zeros ou uma coluna de zeros, o determinante será igual a zero.
- O determinante de uma matriz inversa\(A^{−1}\) é o inverso do determinante da matriz\(A\).
- Se qualquer linha ou coluna for multiplicada por uma constante, o determinante será multiplicado pelo mesmo fator.
Ilustre cada uma das propriedades dos determinantes.
Solução
A propriedade 1 afirma que, se a matriz estiver na forma triangular superior, o determinante é o produto das entradas abaixo da diagonal principal.
\(A=\begin{bmatrix}1&2&3\\0&2&1\\0&0&−1\end{bmatrix}\)
Aumente\(A\) com as duas primeiras colunas.
\(A=\left[ \begin{array}{ccc|cc}1&2&3&1&2\\0&2&1&0&2\\0&0&−1&0&0\end{array}\right]\)
Então
\[\begin{align*} \det(A)&= 1(2)(-1)+2(1)(0)+3(0)(0)-0(2)(3)-0(1)(1)+1(0)(2)\\ &= -2 \end{align*}\]
A propriedade 2 afirma que a troca de linhas altera o sinal. Dado
\[\begin{align*} A&=\begin{bmatrix}-1&5\\4&-3\end{bmatrix}\\ \det(A)&= (-1)(-3)-(4)(5)\\ &= 3-20\\ &= -17 \end{align*}\]
\[\begin{align*} B&= \begin{bmatrix}4&-3\\-1&5\end{bmatrix}\\ \det(B)&= (4)(5)-(-1)(-3)\\ &= 20-3\\ &= 17 \end{align*}\]
A propriedade 3 afirma que se duas linhas ou duas colunas forem idênticas, o determinante será igual a zero.
\[\begin{align*} A&=\left[ \begin{array}{ccc|cc}1&2&2&1&2\\2&2&2&2&2\\-1&2&2&-1&2\end{array}\right]\\ \det(A)&=1(2)(2)+2(2)(-1)+2(2)(2)+1(2)(2)-2(2)(1)-2(2)(2)\\ &=4-4+8+4-4-8\\ &=0 \end{align*}\]
A propriedade 4 afirma que se uma linha ou coluna for igual a zero, o determinante será igual a zero. Assim,
\[\begin{align*} A&=\begin{bmatrix}1&2\\0&0\end{bmatrix}\\ \det(A)&=1(0)-2(0)\\ &=0 \end{align*}\]
A propriedade 5 afirma que o determinante de uma matriz inversa\(A^{−1}\) é o recíproco do determinante\(A\). Assim,
\[\begin{align*} A&=\begin{bmatrix}1&2\\3&4\end{bmatrix}\\ \det(A)&=1(4)-3(2)\\ &=-2 \end{align*}\]
\[\begin{align*} A^{-1}&=\begin{bmatrix}-2&1\\\dfrac{3}{2}&-\dfrac{1}{2}\end{bmatrix}\\ \det(A^{-1})&=-2\left(-\dfrac{1}{2}\right)-\dfrac{3}{2}(1)\\ &=-\dfrac{1}{2} \end{align*}\]
A propriedade 6 afirma que se qualquer linha ou coluna de uma matriz for multiplicada por uma constante, o determinante será multiplicado pelo mesmo fator. Assim,
\[\begin{align*} A&=\begin{bmatrix}1&2\\3&4\end{bmatrix}\\ \det(A)&=1(4)-2(3)\\ &=-2 \end{align*}\]
\[\begin{align*} B&=\begin{bmatrix}2(1)&2(2)\\3&4\end{bmatrix}\\ \det(B)&=2(4)-3(4)\\ &=-4 \end{align*}\]
Encontre a solução para o\(3 × 3\) sistema fornecido.
\[\begin{align} 2x+4y+4z&=2 \label{eq8}\\ 3x+7y+7z&=-5 \label{eq9}\\ x+2y+2z&=4 \label{eq10}\end{align}\]
Solução
Usando a regra de Cramer, temos
\(D=\begin{bmatrix}2&4&4\\3&7&7\\1&2&2\end{bmatrix}\)
Observe que a segunda e a terceira colunas são idênticas. De acordo com a Propriedade 3, o determinante será zero, então não há solução ou um número infinito de soluções. Temos que realizar a eliminação para descobrir.
1. Multiplique a Equação\ ref {eq10} por\(–2\) e adicione o resultado à Equação\ ref {eq8}.
\[\begin{align*} -2x-4y-4x&=-8\\ 2x+4y+4z&=2\\ 0&=-6 \end{align*}\]
Obter uma declaração que é uma contradição significa que o sistema não tem solução.
Acesse esses recursos on-line para obter instruções e práticas adicionais com a Regra de Cramer.
Conceitos-chave
- O determinante para\(\begin{bmatrix}a&b\\c&d\end{bmatrix}\) é\(ad−bc\). Veja o exemplo\(\PageIndex{1}\).
- A Regra de Cramer substitui uma coluna variável pela coluna constante. As soluções são\(x=\dfrac{D_x}{D}\),\(y=\dfrac{D_y}{D}\). Veja o exemplo\(\PageIndex{2}\).
- Para encontrar o determinante de uma\(3×3\) matriz, aumente com as duas primeiras colunas. Adicione as três entradas diagonais (superior esquerdo para inferior direito) e subtraia as três entradas diagonais (inferior esquerdo para superior direito). Veja o exemplo\(\PageIndex{3}\).
- Para resolver um sistema de três equações em três variáveis usando a Regra de Cramer, substitua uma coluna variável pela coluna constante para cada solução desejada:\(x=\dfrac{D_x}{D}\),\(y=\dfrac{D_y}{D}\),\(z=\dfrac{D_z}{D}\). Veja o exemplo\(\PageIndex{4}\).
- A Regra de Cramer também é útil para encontrar a solução de um sistema de equações sem solução ou soluções infinitas. Veja o exemplo\(\PageIndex{5}\) e o exemplo\(\PageIndex{6}\).
- Certas propriedades dos determinantes são úteis para resolver problemas. Por exemplo:
- Se a matriz estiver na forma triangular superior, o determinante é igual ao produto das entradas abaixo da diagonal principal.
- Quando duas linhas são trocadas, o sinal de mudança determinante.
- Se duas linhas ou duas colunas forem idênticas, o determinante será igual a zero.
- Se uma matriz contiver uma linha de zeros ou uma coluna de zeros, o determinante será igual a zero.
- O determinante de uma matriz inversa\(A^{−1}\) é o inverso do determinante da matriz\(A\).
- Se qualquer linha ou coluna for multiplicada por uma constante, o determinante será multiplicado pelo mesmo fator. Veja o exemplo\(\PageIndex{7}\) e o exemplo\(\PageIndex{8}\).


