9.E: Sistemas de equações e desigualdades (exercícios)

Last updated
Save as PDF

Page ID: 189153

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

9.1: Sistemas de equações lineares: duas variáveis

Verbal

1) Um sistema de equações lineares pode ter exatamente duas soluções? Explique por que ou por que não.

Resposta: Não, você pode ter zero, um ou infinitamente muitos. Examine os gráficos.

2) Se você estiver realizando uma análise de equilíbrio para uma empresa e suas equações de custo e receita forem dependentes, explique o que isso significa para as margens de lucro da empresa.

3) Se você estiver resolvendo uma análise de equilíbrio e obtiver um ponto de equilíbrio negativo, explique o que isso significa para a empresa?

Resposta: Isso significa que não há um ponto de equilíbrio realista. No momento em que a empresa produz uma unidade, ela já está lucrando.

4) Se você estiver resolvendo uma análise de equilíbrio e não houver um ponto de equilíbrio, explique o que isso significa para a empresa. Como eles devem garantir que haja um ponto de equilíbrio?

5) Dado um sistema de equações, explique pelo menos dois métodos diferentes para resolver esse sistema.

Resposta: Você pode resolver por substituição (isolando$x$ ou$y$), graficamente ou por adição.

Algébrico

Para os exercícios 6-10, determine se o par ordenado dado é uma solução para o sistema de equações.

6)$\begin{align*} 5x-y &= 4\\ x+6y &= 2 \end{align*}\; \text{ and } (4,0)$

7)$\begin{align*} -3x-5y &= 13\\ -x+4y &= 10 \end{align*}\; \text{ and } (-6,1)$

Resposta: sim

8)$\begin{align*} 3x+7y &= 1\\ 2x+4y &= 0 \end{align*}\; \text{ and } (2,3)$

9)$\begin{align*} -2x+5y &= 7\\ 2x+9y &= 7 \end{align*}\; \text{ and } (-1,1)$

Resposta: sim

10)$\begin{align*} x+8y &= 43\\ 3x-2y &= -1 \end{align*}\; \text{ and } (3,5)$

Para os exercícios 11-20, resolva cada sistema por substituição.

11)$\begin{align*} x+5y &= 5\\ 2x+3y &= 4 \end{align*}$

Resposta: $(-1,2)$

12)$\begin{align*} 3x-2y &= 18\\ 5x+10y &= -10 \end{align*}$

13)$\begin{align*} 4x+2y &= -10\\ 3x+9y &= 0 \end{align*}$

Resposta: $(-3,1)$

14)$\begin{align*} 2x+4y &= -3.8\\ 9x-5y &= 1.3 \end{align*}$

15)$\begin{align*} -2x+3y &= 1.2\\ -3x-6y &= 1.8 \end{align*}$

Resposta: $\left ( -\dfrac{3}{5},0 \right )$

16)$\begin{align*} x-0.2y &= 1\\ -10x+2y &= 5 \end{align*}$

17)$\begin{align*} 3x+5y &= 9\\ 30x+50y &= -90 \end{align*}$

Resposta: Não existem soluções

18)$\begin{align*} -3x+y &= 2\\ 12x-4y &= -8 \end{align*}$

19)$\begin{align*} \dfrac{1}{2}x+\dfrac{1}{3}y &= 16\\ \dfrac{1}{6}x+\dfrac{1}{4}y &= 9 \end{align*}$

Resposta: $\left ( \dfrac{72}{5},\dfrac{132}{5} \right )$

20)$\begin{align*} -\dfrac{1}{4}x+\dfrac{3}{2}y &= 11\\ -\dfrac{1}{8}x+\dfrac{1}{3}y &= 3 \end{align*}$

Para os exercícios 21-30, resolva cada sistema por adição.

21)$\begin{align*} -2x+5y &= -42\\ 7x+2y &= 30 \end{align*}$

Resposta: $(6,-6)$

22)$\begin{align*} 6x-5y &= -34\\ 2x+6y &= 4 \end{align*}$

23)$\begin{align*} 5x-y &= -2.6\\ -4x-6y &= 1.4 \end{align*}$

Resposta: $\left ( -\dfrac{1}{2},\dfrac{1}{10} \right )$

24)$\begin{align*} 7x-2y &= 3\\ 4x+5y &= 3.25 \end{align*}$

25)$\begin{align*} -x+2y &= -1\\ 5x-10y &= 6 \end{align*}$

Resposta: Não existem soluções

26)$\begin{align*} 7x+6y &= 2\\ -28x-24y &= -8 \end{align*}$

27)$\begin{align*} \dfrac{5}{6}x+\dfrac{1}{4}y &= 0\\ \dfrac{1}{8}x-\dfrac{1}{2}y &= -\dfrac{43}{120} \end{align*}$

Resposta: $\left ( -\dfrac{1}{5},\dfrac{2}{3} \right )$

28)$\begin{align*} \dfrac{1}{3}x+\dfrac{1}{9}y &= \dfrac{2}{9}\\ -\dfrac{1}{2}x+\dfrac{4}{5}y &= -\dfrac{1}{3} \end{align*}$

29)$\begin{align*} -0.2x+0.4y &= 0.6\\ x-2y &= -3 \end{align*}$

Resposta: $\left ( x,\dfrac{x+3}{2} \right )$

30)$\begin{align*} -0.1x+0.2y &= 0.6\\ 5x-10y &= 1 \end{align*}$

Para os exercícios 31-40, resolva cada sistema por qualquer método.

31)$\begin{align*} 5x+9y &= 16\\ x+2y &= 4 \end{align*}$

Resposta: $(-4,4)$

32)$\begin{align*} 6x-8y &= -0.6\\ 3x+2y &= 0.9 \end{align*}$

33)$\begin{align*} 5x-2y &= 2.25\\ 7x-4y &= 3 \end{align*}$

Resposta: $\left ( \dfrac{1}{2},\dfrac{1}{8} \right )$

34)$\begin{align*} x-\dfrac{5}{12}y &= -\dfrac{55}{12}\\ -6x+\dfrac{5}{2}y &= \dfrac{55}{2} \end{align*}$

(35)$\begin{align*} 7x-4y &= \dfrac{7}{6}\\ 2x+4y &= \dfrac{1}{3} \end{align*}$

Resposta: $\left ( \dfrac{1}{6},0 \right )$

36)$\begin{align*} 3x+6y &= 11\\ 2x+4y &= 9 \end{align*}$

37)$\begin{align*} \dfrac{7}{3}x-\dfrac{1}{6}y &= 2\\ -\dfrac{21}{6}x+\dfrac{3}{12}y &= -3 \end{align*}$

Resposta: $(x,2(7x-6))$

38)$\begin{align*} \dfrac{1}{2}x+\dfrac{1}{3}y &= \dfrac{1}{3}\\ \dfrac{3}{2}x+\dfrac{1}{4}y &= -\dfrac{1}{8} \end{align*}$

39)$\begin{align*} 2.2x+1.3y &= -0.1\\ 4.2x+4.2y &= 2.1 \end{align*}$

Resposta: $\left ( -\dfrac{5}{6},\dfrac{4}{3} \right )$

40)$\begin{align*} 0.1x+0.2y &= 2\\ 0.35x-0.3y &= 0 \end{align*}$

Gráfica

Para os exercícios 41-45, represente graficamente o sistema de equações e indique se o sistema é consistente, inconsistente ou dependente e se o sistema tem uma solução, nenhuma solução ou soluções infinitas.

41)$\begin{align*} 3x-y &= 0.6\\ x-2y &= 1.3 \end{align*}$

Resposta: Consistente com uma solução

(42)$\begin{align*} -x+2y &= 4\\ 2x-4y &= 1 \end{align*}$

43)$\begin{align*} x+2y &= 7\\ 2x+6y &= 12 \end{align*}$

Resposta: Consistente com uma solução

44)$\begin{align*} 3x-5y &= 7\\ x-2y &= 3 \end{align*}$

45)$\begin{align*} 3x-2y &= 5\\ -9x+6y &= -15 \end{align*}$

Resposta: Depende de infinitas soluções

Tecnologia

Para os exercícios 46-50, use a função de interseção em um dispositivo gráfico para resolver cada sistema. Arredonde todas as respostas para o centésimo mais próximo.

(46)$\begin{align*} 0.1x+0.2y &= 0.3\\ -0.3x+0.5y &= 1 \end{align*}$

47)$\begin{align*} -0.01x+0.12y &= 0.62\\ 0.15x+0.20y &= 0.52 \end{align*}$

Resposta: $(-3.08,4.91)$

48)$\begin{align*} 0.5x+0.3y &= 4\\ 0.25x-0.9y &= 0.46 \end{align*}$

49)$\begin{align*} 0.15x+0.27y &= 0.39\\ -0.34x+0.56y &= 1.8 \end{align*}$

Resposta: $(-1.52,2.29)$

50)$\begin{align*} -0.71x+0.92y &= 0.13\\ 0.83x+0.05y &= 2.1 \end{align*}$

Extensões

Para os exercícios 51-55, resolva cada sistema em termos de$A, B, C, D,$ e$F$ onde$A-F$ estão números diferentes de zero. Observe isso$A\neq B$$AE\neq BD$ e.

51)$\begin{align*} x+y &= A\\ x-y &= B \end{align*}$

Resposta: $\left ( \dfrac{A+B}{2},\dfrac{A-B}{2} \right )$

52)$\begin{align*} x+Ay &= 1\\ x+By &= 1 \end{align*}$

53)$\begin{align*} Ax+y &= 0\\ Bx+y &= 1 \end{align*}$

Resposta: $\left ( \dfrac{-1}{A-B},\dfrac{A}{A-B} \right )$

54)$\begin{align*} Ax+By &= C\\ x+y &= 1 \end{align*}$

55)$\begin{align*} Ax+By &= C\\ Dx+Ey &= F \end{align*}$

Resposta: $\left ( \dfrac{CE-BF}{BD-AE},\dfrac{AF-CD}{BD-AE} \right )$

Aplicativos do mundo real

Para os exercícios 56-60, resolva a quantidade desejada.

56) Uma empresa de bichos de pelúcia tem um custo total de produção$C=12x+30$ e uma função de receita$R=20x$. Encontre o ponto de equilíbrio.

57) Um restaurante de fast-food tem um custo de produção$C(x)=11x+120$ e uma função de receita$R(x)=5x$. Quando a empresa começa a lucrar?

Resposta: Eles nunca dão lucro.

58) Uma fábrica de telefones celulares tem um custo de produção$C(x)=150x+10,000$ e uma função de receita$R(x)=200x$. Qual é o ponto de equilíbrio?

59) Um músico cobra$C(x)=64x+20,000$, onde$x$ está o número total de participantes do show. O local cobra$\$80$ por ingresso. Depois de quantas pessoas comprarem ingressos, o local se equilibra, e qual é o valor do total de ingressos vendidos naquele momento?

Resposta: $(1,250, 100,000)$

60) Uma fábrica de guitarras tem um custo de produção$C(x)=75x+50,000$. Se a empresa precisar se equilibrar após a venda$150$ das unidades, a que preço eles deveriam vender cada guitarra? Arredonde para o dólar mais próximo e escreva a função de receita.

Para os exercícios 61-77, use um sistema de equações lineares com duas variáveis e duas equações para resolver.

61) Encontre dois números cuja soma é$28$ e diferença é$13$.

Resposta: Os números são$7.5$ e$20.5$

62) Um número é$9$ mais do que outro número. O dobro da soma dos dois números é$10$. Encontre os dois números.

63) O custo inicial de um restaurante é$\$120,000$, e cada refeição custa$\$10$ para o restaurante fazer. Se cada refeição for vendida$\$15$, depois de quantas refeições o restaurante se equilibra?

Resposta: $24,000$

64) Uma empresa de mudanças cobra uma taxa fixa de$\$150$, e um adicional$\$5$ para cada caixa. Se um serviço de táxi cobrasse$\$20$ por cada caixa, quantas caixas você precisaria para que fosse mais barato usar a empresa de mudanças e qual seria o custo total?

65) Um total de estudantes universitários do$1,595$ primeiro e segundo ano se reuniram em um comício estimulante. O número de calouros excedeu o número de alunos do segundo ano em$15$. Quantos calouros e alunos do segundo ano estavam presentes?

Resposta: $790$alunos do segundo ano,$805$ calouros

66)$276$ alunos matriculados em uma aula de química de nível calouro. No final do semestre,$5$ vezes o número de alunos aprovados como reprovados. Encontre o número de alunos aprovados e o número de alunos que foram reprovados.

67) Havia$130$ professores em uma conferência. Se houvesse$18$ mais mulheres do que homens presentes, quantas pessoas de cada gênero compareceram à conferência?

Resposta: $56$homens,$74$ mulheres

68) Um jipe e um BMW entram em uma rodovia que vai de leste a oeste na mesma saída em direções opostas. O jipe entrou na rodovia$30$ minutos antes do BMW, e viajou$7$ mph mais devagar que o BMW. Depois de$2$ horas a partir do momento em que a BMW entrou na rodovia, os carros estavam a$306.5$ quilômetros de distância. Encontre a velocidade de cada carro, supondo que eles tenham sido conduzidos no controle de cruzeiro.

69) Se um cientista misturasse solução$10\%$ salina com solução$60\%$ salina para obter$25$ galões de solução$40\%$ salina, quantos galões de$10\%$$60\%$ solução salina foram misturados?

Resposta: $10$galões de$10\%$ solução,$15$ galões de$60\%$ solução

70) Uma investidora obteve o triplo dos lucros do que ela ganhou no ano passado. Se ela obtivesse o$\$500,000.48$ total dos dois anos, quanto ela ganhava em lucros a cada ano?

71) Um investidor que se dedica ao setor imobiliário investiu$1.1$ milhões de dólares em dois investimentos em terras. No primeiro investimento, Swan Peak, seu retorno foi um$110\%$ aumento no dinheiro que ela investiu. No segundo investimento, Riverside Community, ela ganhou$50\%$ mais do que investiu. Se ela ganhou$\$1$ milhões em lucros, quanto ela investiu em cada um dos negócios de terras?

Resposta: Pico do Cisne:$\$750,000$, Riverside:$\$350,000$

72) Se um investidor investe um total de$\$25,000$ em dois títulos, um que paga juros$3\%$ simples e outro que paga$2\dfrac{7}{8}\%$ juros, e o investidor ganha juros$\$737.50$ anuais, quanto foi investido em cada conta?

73) Se um investidor$\$23,000$ investe em dois títulos, um que paga$4\%$ com juros simples e o outro pagando juros$2\%$ simples, e o investidor ganha juros$\$710.00$ anuais, quanto foi investido em cada conta?

Resposta: $\$12,500$na primeira conta,$\$10,500$ na segunda conta.

74) Os CDs custam$\$5.96$ mais do que os DVDs em All Bets Are Off Electronics. Quanto custariam$6$ CDs e$2$ DVDs se os$5$ CDs e$2$ DVDs custassem$\$127.73$?

75) Um funcionário da loja vendeu$60$ pares de tênis. As capotas altas vendidas$\$98.99$ e as de cano baixo vendidas por$\$129.99$. Se as receitas dos dois tipos de vendas totalizaram$\$6,404.40$, quantos de cada tipo de tênis foram vendidos?

Resposta: Topo alto:$45$, cano baixo:$15$

76) Um gerente de concertos contou os recibos dos$350$ ingressos no dia seguinte ao show. O preço de uma passagem estudantil era$\$12.50$, e o preço de uma passagem para adultos era$\$16.00$. O registro confirma que$\$5,075$ foi recolhido. Quantos ingressos para estudantes e adultos foram vendidos?

77) A entrada em um parque de diversões para$4$ crianças e$2$ adultos é$\$116.90$. Para$6$ crianças e$3$ adultos, a admissão é$\$175.35$. Supondo um preço diferente para crianças e adultos, qual é o preço do ingresso para crianças e o preço do ingresso para adultos?

Resposta: Infinitas soluções. Precisamos de mais informações.

9.2: Sistemas de equações lineares: três variáveis

Verbal

1) Um sistema linear de três equações pode ter exatamente duas soluções? Explique por que ou por que não

Resposta: Não, só pode haver uma, zero ou infinitas soluções.

2) Se um determinado triplo ordenado resolve o sistema de equações, essa solução é única? Se sim, explique o porquê. Caso contrário, dê um exemplo em que não seja único.

3) Se um determinado triplo ordenado não resolver o sistema de equações, não há solução? Se sim, explique o porquê. Se não, dê um exemplo.

Resposta

Não necessariamente. Pode haver zero, uma ou infinitas soluções. Por exemplo, não$(0,0,0)$ é uma solução para o sistema abaixo, mas isso não significa que ele não tenha solução.

$\begin{align*} 2x+3y-6z &= 1\\ -4x-6y+12z &= -2\\ x+2y+5z &= 10 \end{align*}$

4) Usando o método de adição, existe apenas uma maneira de resolver o sistema?

5) Você pode explicar se só pode haver um método para resolver um sistema linear de equações? Se sim, dê um exemplo desse sistema de equações. Se não, explique por que não.

Resposta: Cada sistema de equações pode ser resolvido graficamente, por substituição e por adição. No entanto, sistemas de três equações se tornam muito complexos de resolver graficamente, então outros métodos geralmente são preferíveis.

Algébrico

Para os exercícios 6-10, determine se o triplo ordenado dado é a solução para o sistema de equações.

6)$\begin{align*} 2x-6y+6z &= -12\\ x+4y+5z &= -1\\ -x+2y+3z &= -1 \end{align*}\; \; \text{ and }\; (0,1,-1)$

7)$\begin{align*} 6x-y+3z &= 6\\ 3x+5y+2z &= 0\\ x+y &= 0 \end{align*}\; \; \text{ and }\; (3,-3,-5)$

Resposta: Não

8)$\begin{align*} 6x-7y+z &= 2\\ -x-y+3z &= 4\\ 2x+y-z &= 1 \end{align*}\; \; \text{ and }\; (4,2,-6)$

9)$\begin{align*} x-y &= 0\\ x-z &= 5\\ x-y+z &= -1 \end{align*}\; \; \text{ and }\; (4,4,-1)$

Resposta: sim

10)$\begin{align*} -x-y+2z &= 3\\ 5x+8y-3z &= 4\\ -x+3y-5z &= -5 \end{align*}\; \; \text{ and }\; (4,1,-7)$

Para os exercícios 11-16, resolva cada sistema por substituição.

11)$\begin{align*} 3x-4y+2z &= -15\\ 2x+4y+z &= 16\\ 2x+3y+5z &= 20 \end{align*}$

Resposta: $(-1,4,2)$

12)$\begin{align*} 5x-2y+3z &= 20\\ 2x-4y-3z &= -9\\ x+6y-8z &= 21 \end{align*}$

13)$\begin{align*} 5x+2y+4z &= 9\\ -3x+2y+z &= 10\\ 4x-3y+5z &= -3 \end{align*}$

Resposta: $\left ( -\dfrac{85}{107},\dfrac{312}{107},\dfrac{191}{107} \right )$

14)$\begin{align*} 4x-3y+5z &= 31\\ -x+2y+4z &= 20\\ x+5y-2z &= -29 \end{align*}$

15)$\begin{align*} 5x-2y+3z &= 4\\ -4x+6y-7z &= -1\\ 3x+2y-z &= 4 \end{align*}$

Resposta: $\left ( 1,\dfrac{1}{2},0 \right )$

16)$\begin{align*} 4x+6y+9z &= 4\\ -5x+2y-6z &= 3\\ 7x-4y+3z &= -3 \end{align*}$

Para os exercícios 17-45, resolva cada sistema por eliminação gaussiana.

17)$\begin{align*} 2x-y+3z &= 17\\ -5x+4y-2z &= -46\\ 2y+5z &= -7 \end{align*}$

Resposta: $(4,-6,1)$

18)$\begin{align*} 5x-6y+3z &= 50\\ -x+4y &= 10\\ 2x-z &= 10 \end{align*}$

19)$\begin{align*} 2x+3y-6z &= 1\\ -4x-6y+12z &= -2\\ x+2y+5z &= 10 \end{align*}$

Resposta: $\left ( x,\dfrac{1}{27}(65-16x),\dfrac{x+28}{27} \right )$

20)$\begin{align*} 4x+6y-2z &= 8\\ 6x+9y-3z &= 12\\ -2x-3y+z &= -4 \end{align*}$

21)$\begin{align*} 2x+3y-4z &= 5\\ -3x+2y+z &= 11\\ -x+5y+3z &= 4 \end{align*}$

Resposta: $\left ( -\dfrac{45}{13},\dfrac{17}{13},-2 \right )$

22)$\begin{align*} 10x+2y-14z &= 8\\ -x-2y-4z &= -1\\ -12x-6y+6z &= -12 \end{align*}$

23)$\begin{align*} x+y+z &= 14\\ 2y+3z &= -14\\ -16y-24z &= -112 \end{align*}$

Resposta: Não existem soluções

24)$\begin{align*} 5x-3y+4z &= -1\\ -4x+2y-3z &= 0\\ -x+5y+7z &= -11 \end{align*}$

25)$\begin{align*} x+y+z &= 0\\ 2x-y+3z &= 0\\ x-z &= 0 \end{align*}$

Resposta: $(0,0,0)$

26)$\begin{align*} 3x+2y-5z &= 6\\ 5x-4y+3z &= -12\\ 4x+5y-2z &= 15 \end{align*}$

27)$\begin{align*} x+y+z &= 0\\ 2x-y+3z &= 0\\ x-z &= 1 \end{align*}$

Resposta: $\left ( \dfrac{4}{7},-\dfrac{1}{7},-\dfrac{3}{7} \right )$

28)$\begin{align*} 3x-\dfrac{1}{2}y-z &= -\dfrac{1}{2}\\ 4x+z &= 3\\ -x+\dfrac{3}{2}y &= \dfrac{5}{2} \end{align*}$

29)$\begin{align*} 6x-5y+6z &= 38\\ \dfrac{1}{5}x-\dfrac{1}{2}y+\dfrac{3}{5}z &= 1\\ -4x-\dfrac{3}{2}y-z &= -74 \end{align*}$

Resposta: $(7,20,16)$

30)$\begin{align*} \dfrac{1}{2}x-\dfrac{1}{5}y+\dfrac{2}{5}z &= -\dfrac{13}{10}\\ \dfrac{1}{4}x-\dfrac{2}{5}y-\dfrac{1}{5}z &= -\dfrac{7}{20}\\ -\dfrac{1}{2}x-\dfrac{3}{4}y-\dfrac{1}{2}z &= -\dfrac{5}{4} \end{align*}$

31)$\begin{align*} -\dfrac{1}{3}x-\dfrac{1}{2}y-\dfrac{1}{4}z &= \dfrac{3}{4}\\ -\dfrac{1}{2}x-\dfrac{1}{4}y-\dfrac{1}{2}z &= 2\\ -\dfrac{1}{4}x-\dfrac{3}{4}y-\dfrac{1}{2}z &= -\dfrac{1}{2} \end{align*}$

Responda: $(-6,2,1)$

32)$\begin{align*} \dfrac{1}{2}x-\dfrac{1}{4}y+\dfrac{3}{4}z &= 0\\ \dfrac{1}{4}x-\dfrac{1}{10}y+\dfrac{2}{5}z &= -2\\ \dfrac{1}{8}x+\dfrac{1}{5}y-\dfrac{1}{8}z &= 2 \end{align*}$

33)$\begin{align*} \dfrac{4}{5}x-\dfrac{7}{8}y+\dfrac{1}{2}z &= 1\\ -\dfrac{4}{5}x-\dfrac{3}{4}y+\dfrac{1}{3}z &= -8\\ -\dfrac{2}{5}x-\dfrac{7}{8}y+\dfrac{1}{2}z &= -5 \end{align*}$

Responda: $(5,12,15)$

34)$\begin{align*} -\dfrac{1}{3}x-\dfrac{1}{8}y+\dfrac{1}{6}z &= -\dfrac{4}{3}\\ -\dfrac{2}{3}x-\dfrac{7}{8}y+\dfrac{1}{3}z &= -\dfrac{23}{3}\\ -\dfrac{1}{3}x-\dfrac{5}{8}y+\dfrac{5}{6}z &= 0 \end{align*}$

(35)$\begin{align*} -\dfrac{1}{4}x-\dfrac{5}{4}y+\dfrac{5}{2}z &= -5\\ -\dfrac{1}{2}x-\dfrac{5}{3}y+\dfrac{5}{4}z &= \dfrac{55}{12}\\ -\dfrac{1}{3}x-\dfrac{1}{3}y+\dfrac{1}{3}z &= \dfrac{5}{3} \end{align*}$

Responda: $(-5,-5,-5)$

36)$\begin{align*} \dfrac{1}{40}x+\dfrac{1}{60}y+\dfrac{1}{80}z &= \dfrac{1}{100}\\ -\dfrac{1}{2}x-\dfrac{1}{3}y-\dfrac{1}{4}z &= -\dfrac{1}{5}\\ \dfrac{3}{8}x+\dfrac{3}{12}y+\dfrac{3}{16}z &= \dfrac{3}{20} \end{align*}$

37)$\begin{align*} 0.1x-0.2y+0.3z &= 2\\ 0.5x-0.1y+0.4z &= 8\\ 0.7x-0.2y+0.3z &= 8 \end{align*}$

Responda: $(10,10,10)$

38)$\begin{align*} 0.2x+0.1y-0.3z &= 0.2\\ 0.8x+0.4y-1.2z &= 0.1\\ 1.6x+0.8y-2.4z &= 0.2 \end{align*}$

39)$\begin{align*} 1.1x+0.7y-3.1z &= -1.79\\ 2.1x+0.5y-1.6z &= -0.13\\ 0.5x+0.4y-0.5z &= -0.07 \end{align*}$

Responda: $\left ( \dfrac{1}{2},\dfrac{1}{5},\dfrac{4}{5} \right )$

40)$\begin{align*} 0.5x-0.5y+0.5z &= 10\\ 0.2x-0.2y+0.2z &= 4\\ 0.1x-0.1y+0.1z &= 2 \end{align*}$

41)$\begin{align*} 0.1x+0.2y+0.3z &= 0.37\\ 0.1x-0.2y-0.3z &= -0.27\\ 0.5x-0.1y-0.3z &= -0.03 \end{align*}$

Responda: $\left ( \dfrac{1}{2},\dfrac{2}{5},\dfrac{4}{5} \right )$

(42)$\begin{align*} 0.5x-0.5y-0.3z &= 0.13\\ 0.4x-0.1y-0.3z &= 0.11\\ 0.2x-0.8y-0.9z &= -0.32 \end{align*}$

43)$\begin{align*} 0.5x+0.2y-0.3z &= 1\\ 0.4x-0.6y+0.7z &= 0.8\\ 0.3x-0.1y-0.9z &= 0.6 \end{align*}$

Responda: $(2,0,0)$

44)$\begin{align*} 0.3x+0.3y+0.5z &= 0.6\\ 0.4x+0.4y+0.4z &= 1.8\\ 0.4x+0.2y+0.1z &= 1.6 \end{align*}$

45)$\begin{align*} 0.8x+0.8y+0.8z &= 2.4\\ 0.3x-0.5y+0.2z &= 0\\ 0.1x+0.2y+0.3z &= 0.6 \end{align*}$

Responda: $(1,1,1)$

Extensões

Para os exercícios 46-50, resolva o sistema para$x,y,$$z$ e.

(46)$\begin{align*} x+y+z &= 3\\ \dfrac{x-1}{2}+\dfrac{y-3}{2}+\dfrac{z+1}{2} &= 0\\ \dfrac{x-2}{3}+\dfrac{y+4}{3}+\dfrac{z-3}{3} &= \dfrac{2}{3} \end{align*}$

47)$\begin{align*} 5x-3y-\dfrac{z+1}{2} &= \dfrac{1}{2}\\ 6x+\dfrac{y-9}{2}+2z &= -3\\ \dfrac{x+8}{2}-4y+z &= 4\end{align*}$

Responda: $\left ( \dfrac{128}{557},\dfrac{23}{557},\dfrac{428}{557} \right )$

48)$\begin{align*} \dfrac{x+4}{7}-\dfrac{y-1}{6}+\dfrac{z+2}{3} &= 1\\ \dfrac{x-2}{4}+\dfrac{y+1}{8}-\dfrac{z+8}{2} &= 0\\ \dfrac{x+6}{3}-\dfrac{y+2}{3}+\dfrac{z+4}{2} &= 3 \end{align*}$

49)$\begin{align*} \dfrac{x-3}{6}+\dfrac{y+2}{2}-\dfrac{z-3}{3} &= 2\\ \dfrac{x+2}{4}+\dfrac{y-5}{2}+\dfrac{z+4}{2} &= 1\\ \dfrac{x+6}{2}-\dfrac{y-3}{3}+z+1 &= 9 \end{align*}$

Responda: $(6,-1,0)$

50)$\begin{align*} \dfrac{x-1}{3}+\dfrac{y+3}{4}+\dfrac{z+2}{6} &= 1\\ 4x+3y-2z &= 11\\ 0.02x+0.015y-0.01z &= 0.065 \end{align*}$

Aplicativos do mundo real

51) Três números pares somam$108$. Quanto menor for a metade maior e o número do meio, maior.$\dfrac{3}{4}$ Quais são os três números?

Responda: $24, 36, 48$

52) Três números somam$147$. O menor número é metade do número do meio, que é metade do maior número. Quais são os três números?

53) Em uma reunião familiar, estavam presentes apenas parentes consangüíneos, compostos por filhos, pais e avós. Havia$400$ pessoas no total. Havia duas vezes mais pais do que avós e 50 filhos a mais do que pais. Quantas crianças, pais e avós estavam presentes?

Responda: $70$avós,$140$ pais,$190$ filhos

54) Um abrigo de animais tem um total de$350$ animais compostos por gatos, cães e coelhos. Se o número de coelhos for$5$ menor que a metade do número de gatos e houver$20$ mais gatos do que cães, quantos de cada animal estão no abrigo?

55) Sua colega de quarto, Sarah, se ofereceu para comprar mantimentos para você e sua outra colega de quarto. A conta total foi$\$82$. Ela esqueceu de guardar os recibos individuais, mas lembrou que suas compras eram$\$0.05$ mais baratas do que a metade de suas compras, e que as compras de sua outra colega de quarto eram$\$2.10$ mais do que suas compras. Quanto custou sua parte nas compras?

Responda: Sua parte foi$\$19.95$, a parte de Sarah foi$\$40$, e a parte de sua outra colega de quarto foi$\$22.05$.

56) Seu colega de quarto, John, se ofereceu para comprar utensílios domésticos para você e seu outro colega de quarto. Você mora perto da fronteira de três estados, cada um com um imposto sobre vendas diferente. A quantia total de dinheiro gasta foi$\$100.75$. Seus suprimentos foram comprados com$5\%$ impostos, John com$8\%$ impostos e seu terceiro colega de quarto com imposto sobre$9\%$ vendas. A quantia total de dinheiro gasto sem impostos é$\$93.50$. Se seus suprimentos antes de impostos eram$\$1$ mais da metade dos suprimentos do seu terceiro colega de quarto antes dos impostos, quanto cada um de vocês gastou? Dê sua resposta com e sem impostos.

57) Três colegas de trabalho trabalham para o mesmo empregador. Seus trabalhos são gerente de armazém, gerente de escritório e motorista de caminhão. A soma dos salários anuais do gerente do armazém e do gerente do escritório é$\$82,000$. O gerente do escritório ganha$\$4,000$ mais do que o motorista do caminhão anualmente. Os salários anuais do gerente do armazém e do motorista do caminhão são totais$\$78,000$. Qual é o salário anual de cada um dos colegas de trabalho?

Responda: Existem infinitas soluções; precisamos de mais informações

58) Em um carnaval,$\$2,914.25$ os recibos foram retirados no final do dia. O custo do ingresso de uma criança era$\$20.50$, um ingresso de adulto era$\$29.75$ e um ingresso para idosos era$\$15.25$. Havia duas vezes mais idosos do que adultos presentes e$20$ mais crianças do que idosos. Quantos ingressos para crianças, adultos e idosos foram vendidos?

59) Uma banda local se esgota para seu show. Eles vendem todos os$1,175$ ingressos por uma bolsa total de$\$28,112.50$. Os ingressos tinham o preço de ingressos$\$20$ para estudantes,$\$22.50$ para crianças e$\$29$ para adultos. Se a banda vendeu duas vezes mais ingressos para adultos do que para crianças, quantos de cada tipo foram vendidos?

Responda: $500$estudantes,$225$ crianças e$450$ adultos

60) Em uma bolsa, uma criança tem$325$ moedas que valem a pena$\$19.50$. Havia três tipos de moedas: moedas de um centavo, níquel e moedas de dez centavos. Se a sacola continha o mesmo número de moedas de dez centavos, quantas moedas de cada tipo estavam na sacola?

61) No ano passado, na concessionária de carros Haven's Pond, para um modelo específico da BMW, Jeep, e Toyota, pode-se comprar todos os três carros para um total de$\$140,000$. Este ano, devido à inflação, os mesmos carros custaria$\$151,830$. O custo do BMW aumentou em$8\%$, o Jeep em e o Toyota em$12\%$.$5\%$ Se o preço do Jeep do ano passado foi$\$7,000$ menor que o preço do BMW do ano passado, qual foi o preço de cada um dos três carros no ano passado?

Responda: O BMW era$\$49,636$, o Jeep e o Toyota sim$\$47,727$.$\$42,636$

62) Um recém-formado aproveitou sua educação em negócios e investiu em três investimentos imediatamente após se formar. Ele investiu$\$80,500$ em três contas, uma que pagava juros$4\%$ simples, uma que pagava juros$3\dfrac{1}{8}\%$ simples e outra que pagava juros$2\dfrac{1}{2}\%$ simples. Ele ganhou$\$2,670$ juros no final de um ano. Se o valor do dinheiro investido na segunda conta foi quatro vezes o valor investido na terceira conta, quanto foi investido em cada conta?

63) Você herda um milhão de dólares. Você investe tudo em três contas por um ano. A primeira conta paga de forma$3\%$ composta anualmente, a segunda conta paga de forma$4\%$ composta anualmente e a terceira conta paga de forma$2\%$ composta anualmente. Depois de um ano, você ganha$\$34,000$ em juros. Se você investir quatro vezes o dinheiro na conta que paga$3\%$ em comparação com$2\%$, quanto você investiu em cada conta?

Responda: $\$400,000$na conta que paga$3\%$ juros,$\$500,000$ na conta que paga$4\%$ juros e$\$100,000$ na conta que paga$2\%$ juros.

64) Você herda cem mil dólares. Você investe tudo em três contas por um ano. A primeira conta paga de forma$4\%$ composta anualmente, a segunda conta paga de forma$3\%$ composta anualmente e a terceira conta paga de forma$2\%$ composta anualmente. Depois de um ano, você ganha$\$3,650$ em juros. Se você investir cinco vezes o dinheiro na conta que paga$4\%$ em comparação com$3\%$, quanto você investiu em cada conta?

65) Os três principais países em consumo de petróleo em um determinado ano são os seguintes: Estados Unidos, Japão e China. Em milhões de barris por dia, os três principais países consumiram o petróleo$39.8\%$ consumido no mundo. Os Estados Unidos consumiram$0.7\%$ mais de quatro vezes o consumo da China. Os Estados Unidos consumiram$5\%$ mais do que o triplo do consumo do Japão. Qual porcentagem do consumo mundial de petróleo os Estados Unidos, o Japão e a China consumiram?

Responda: Os Estados Unidos consumiram$26.3\%$, o Japão e a China$7.1\%$$6.4\%$, do petróleo mundial.

66) Os três principais países em produção de petróleo no mesmo ano são Arábia Saudita, Estados Unidos e Rússia. Em milhões de barris por dia, os três principais países produtores$31.4\%$ do petróleo produzido no mundo. A Arábia Saudita e os Estados Unidos combinaram a maior$22.1\%$ parte da produção mundial, e a Arábia Saudita produziu$2\%$ mais petróleo do que a Rússia. Qual porcentagem da produção mundial de petróleo a Arábia Saudita, os Estados Unidos e a Rússia produziram?

67) As três principais fontes de importação de petróleo para os Estados Unidos no mesmo ano foram Arábia Saudita, México e Canadá. Os três principais países foram responsáveis pelas importações$47\%$ de petróleo. Os Estados Unidos importaram$1.8\%$ mais da Arábia Saudita do que do México e$1.7\%$ mais da Arábia Saudita do que do Canadá. Qual a porcentagem das importações de petróleo dos Estados Unidos provenientes desses três países?

Responda: Arábia Saudita importada$16.8\%$, Canadá importado$15.1\%$ e México$15.0\%$

68) Os três maiores produtores de petróleo dos Estados Unidos em um determinado ano são o Golfo do México, Texas e Alasca. As três regiões foram responsáveis pela produção$64\%$ de petróleo dos Estados Unidos. O Golfo do México e o Texas combinaram para$47\%$ a produção de petróleo. O Texas produziu$3\%$ mais do que o Alasca. Qual porcentagem da produção de petróleo dos Estados Unidos veio dessas regiões?

69) Em certa época, nos Estados Unidos,$398$ espécies de animais estavam na lista de espécies ameaçadas de extinção. Os principais grupos eram mamíferos, pássaros e peixes, compostos pelas espécies ameaçadas$55\%$ de extinção. Os pássaros representavam$0.7\%$ mais do que os peixes, e os peixes representavam$1.5\%$ mais do que os mamíferos. Qual porcentagem das espécies ameaçadas de extinção vieram de mamíferos, pássaros e peixes?

Responda: Os pássaros eram$19.3\%$$18.6\%$, os peixes eram e os mamíferos eram$17.1\%$ de espécies ameaçadas de extinção

70) O consumo de carne nos Estados Unidos pode ser dividido em três categorias: carne vermelha, aves e peixe. Se o peixe representa$4\%$ menos de um quarto do consumo de aves e o consumo de carne vermelha é$18.2\%$ maior do que o consumo de aves, quais são as porcentagens do consumo de carne?

9.3: Sistemas de equações e desigualdades não lineares: duas variáveis

Verbal

1) Explique se um sistema de duas equações não lineares pode ter exatamente duas soluções. Que tal exatamente três? Se não, explique por que não. Em caso afirmativo, dê um exemplo desse sistema, em forma de gráfico, e explique por que sua escolha fornece duas ou três respostas.

Responda: Um sistema não linear pode ser representativo de dois círculos que se sobrepõem e se cruzam em dois locais, daí duas soluções. Um sistema não linear pode ser representativo de uma parábola e um círculo, onde o vértice da parábola encontra o círculo e os ramos também cruzam o círculo, daí três soluções.

2) Ao representar graficamente uma desigualdade, explique por que precisamos testar apenas um ponto para determinar se uma região inteira é a solução?

3) Quando você representa graficamente um sistema de desigualdades, sempre haverá uma região viável? Se sim, explique o porquê. Caso contrário, dê um exemplo de um gráfico de desigualdades que não tenha uma região viável. Por que não tem uma região viável?

Responda: Não. Não precisa haver uma região viável. Considere um sistema limitado por duas linhas paralelas. Uma desigualdade representa a região acima da linha superior; a outra representa a região abaixo da linha inferior. Nesse caso, nenhum ponto no plano está localizado nas duas regiões; portanto, não há uma região viável.

4) Se você representar graficamente uma função de receita e custo, explique como determinar em quais regiões há lucro.

5) Se você realizar sua análise de equilíbrio e houver mais de uma solução, explique como você determinaria quais valores de x são lucro e quais não são.

Responda: Escolha qualquer número entre cada solução e conecte$C(x)$$R(x)$ e. E se$C(x)<r(x)$>< span="">, then there is profit./span>

Algébrico

Para os exercícios 6-10, resolva o sistema de equações não lineares usando a substituição.

6)$\begin{align*} x+y &= 4\\ x^2 + y^2 &= 9 \end{align*}$

7)$\begin{align*} y &= x-3\\ x^2 + y^2 &= 9 \end{align*}$

Responda: $(0,-3)$,$(3,0)$

8)$\begin{align*} y &= x\\ x^2 + y^2 &= 9 \end{align*}$

9)$\begin{align*} y &= -x\\ x^2 + y^2 &= 9 \end{align*}$

Responda: $\left ( -\dfrac{3\sqrt{2}}{2},\dfrac{3\sqrt{2}}{2} \right )$,$\left ( \dfrac{3\sqrt{2}}{2},-\dfrac{3\sqrt{2}}{2} \right )$

10)$\begin{align*} x &= 2\\ x^2 - y^2 &= 9 \end{align*}$

Para os exercícios 11-15, resolva o sistema de equações não lineares usando a eliminação.

11)$\begin{align*} 4x^2 - 9y^2 &= 36\\ 4x^2 + 9y^2 &= 36 \end{align*}$

Responda: $(-3,0)$,$(3,0)$

12)$\begin{align*} x^2 + y^2 &= 25\\ x^2 - y^2 &= 1 \end{align*}$

13)$\begin{align*} 2x^2 + 4y^2 &= 4\\ 2x^2 - 4y^2 &= 25x-10 \end{align*}$

Responda: $\left ( \dfrac{1}{4},-\dfrac{\sqrt{62}}{8} \right )$,$\left ( \dfrac{1}{4},\dfrac{\sqrt{62}}{8} \right )$

14)$\begin{align*} y^2 - x^2 &= 9\\ 3x^2 + 2y^2 &= 8 \end{align*}$

15)$\begin{align*} x^2 + y^2+\dfrac{1}{16} &= 2500\\ y &= 2x^2 \end{align*}$

Responda: $\left ( -\dfrac{\sqrt{398}}{4},\dfrac{199}{4} \right )$,$\left ( \dfrac{\sqrt{398}}{4},\dfrac{199}{4} \right )$

Para os exercícios 16-23, use qualquer método para resolver o sistema de equações não lineares.

16)$\begin{align*} -2x^2+y &= -5\\ 6x-y &= 9 \end{align*}$

17)$\begin{align*} -x^2+y &= 2\\ -x+y &= 2 \end{align*}$

Responda: $(0,2)$,$(1,3)$

18)$\begin{align*} x^2+y^2 &= 1\\ y &= 20x^2-1 \end{align*}$

19)$\begin{align*} x^2+y^2 &= 1\\ y &= -x^2 \end{align*}$

Responda: $\left ( -\sqrt{\dfrac{1}{2}(\sqrt{5}-1)},\dfrac{1}{2}\left (1-\sqrt{5} \right ) \right )$,$\left ( \sqrt{\dfrac{1}{2}(\sqrt{5}-1)},\dfrac{1}{2}\left (1-\sqrt{5} \right ) \right )$

20)$\begin{align*} 2x^3-x^2 &= y\\ y &= \dfrac{1}{2} -x \end{align*}$

21)$\begin{align*} 9x^2+25y^2 &= 225\\ (x-6)^2+y^2 &= 1 \end{align*}$

Responda: $(5,0)$

22)$\begin{align*} x^4-x^2 &= y\\ x^2+y &= 0 \end{align*}$

23)$\begin{align*} 2x^3-x^2 &= y\\ x^2+y &= 0 \end{align*}$

Responda: $(0,0)$

Para os exercícios 24-38, use qualquer método para resolver o sistema não linear.

24)$\begin{align*} x^2+y^2 &= 9\\ y &= 3-x^2 \end{align*}$

25)$\begin{align*} x^2-y^2 &= 9\\ x &= 3 \end{align*}$

Responda: $(3,0)$

26)$\begin{align*} x^2-y^2 &= 9\\ y &= 3 \end{align*}$

27)$\begin{align*} x^2-y^2 &= 9\\ x-y &= 0 \end{align*}$

Responda: Não existem soluções

28)$\begin{align*} -x^2+y &= 2\\ -4x+y &= -1 \end{align*}$

29)$\begin{align*} -x^2+y &= 2\\ 2y &= -x \end{align*}$

Responda: Não existem soluções

30)$\begin{align*} x^2+y^2 &= 25\\ x^2-y^2 &= 36 \end{align*}$

31)$\begin{align*} x^2+y^2 &= 1\\ y^2 &= x^2 \end{align*}$

Responda: $\left ( -\dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{2} \right )$,$\left ( -\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2} \right )$,$\left ( \dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{2} \right )$,$\left ( \dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2} \right )$

32)$\begin{align*} 16x^2-9y^2+144 &= 0\\ y^2 + x^2 &= 16 \end{align*}$

33)$\begin{align*} 3x^2-y^2 &= 12\\ (x-1)^2 + y^2 &= 1 \end{align*}$

Responda: $(2,0)$

34)$\begin{align*} 3x^2-y^2 &= 12\\ (x-1)^2 + y^2 &= 4 \end{align*}$

(35)$\begin{align*} 3x^2-y^2 &= 12\\ x^2 + y^2 &= 16 \end{align*}$

Responda: $(-\sqrt{7},-3)$,$(-\sqrt{7},3)$,$(\sqrt{7},-3)$,$(\sqrt{7},3)$

36)$\begin{align*} x^2-y^2-6x-4y-11 &= 0\\ -x^2 + y^2 &= 5 \end{align*}$

37)$\begin{align*} x^2+y^2-6y &= 7\\ x^2 + y &= 1 \end{align*}$

Responda: $\left ( -\sqrt{\dfrac{1}{2}(\sqrt{73}-5)},\dfrac{1}{2}\left (7-\sqrt{73} \right ) \right )$,$\left ( \sqrt{\dfrac{1}{2}(\sqrt{73}-5)},\dfrac{1}{2}\left (7-\sqrt{73} \right ) \right )$

38)$\begin{align*} x^2+y^2 &= 6\\ xy &= 1 \end{align*}$

Gráfica

Para os exercícios 39-40, represente graficamente a desigualdade.

39)$x^2+y<9$

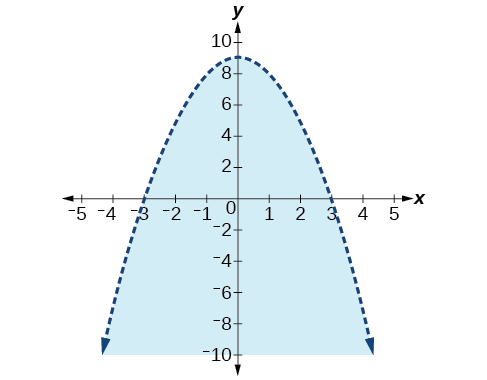
Responda: $CNX_Precalc_Figure_09_03_201.jpg$

40)$x^2+y^2<4$

Para os exercícios 41-45, represente graficamente o sistema de desigualdades. Identifique todos os pontos de interseção.

41)$\begin{align*} x^2 + y &<1 \\ y &>2x \end{align*}$

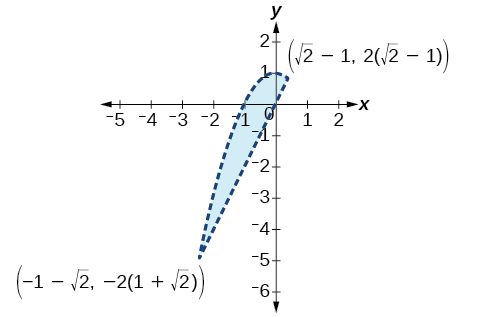
Responda: $CNX_Precalc_Figure_09_03_204.jpg$

(42)$\begin{align*} x^2 + y &<-5 \\ y &>5x+10 \end{align*}$

43)$\begin{align*} x^2 + y^2 &<25 \\ 3x^2 - y^2 &>12 \end{align*}$

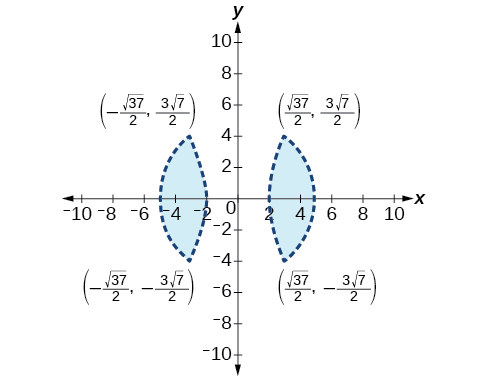
Responda: $CNX_Precalc_Figure_09_03_207.jpg$

44)$\begin{align*} x^2 - y^2 &>-4 \\ x^2 + y^2 &<12 \end{align*}$

45)$\begin{align*} x^2 + 3y^2 &>16 \\ 3x^2 - y^2 &<1 \end{align*}$

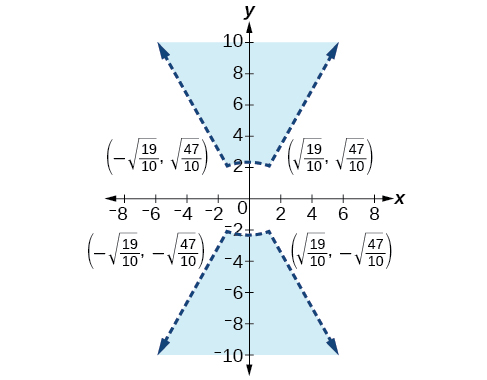
Responda: $CNX_Precalc_Figure_09_03_209.jpg$

Extensões

Para os exercícios 46-47, represente graficamente a desigualdade.

(46)$\begin{align*} y &\geq e^x \\ y &\leq \ln (x)+5 \end{align*}$

47)$\begin{align*} y &\leq -\log (x)\\ y &\leq e^x \end{align*}$

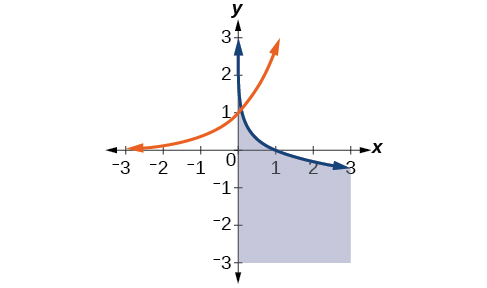
Responda: $CNX_Precalc_Figure_09_03_210.jpg$

Para os exercícios 48-52, encontre as soluções para as equações não lineares com duas variáveis.

48)$\begin{align*} \dfrac{4}{x^2} + \dfrac{1}{y^2} &= 24\\ \dfrac{5}{x^2} - \dfrac{2}{y^2} + 4 &= 0 \end{align*}$

49)$\begin{align*} \dfrac{6}{x^2} - \dfrac{1}{y^2} &= 8\\ \dfrac{1}{x^2} - \dfrac{6}{y^2} &= \dfrac{1}{8} \end{align*}$

Responda: $\left ( -2\sqrt{\dfrac{70}{383}},-2\sqrt{\dfrac{35}{29}} \right )$,$\left ( -2\sqrt{\dfrac{70}{383}},2\sqrt{\dfrac{35}{29}} \right )$,$\left ( 2\sqrt{\dfrac{70}{383}},-2\sqrt{\dfrac{35}{29}} \right )$,$\left ( 2\sqrt{\dfrac{70}{383}},2\sqrt{\dfrac{35}{29}} \right )$

50)$\begin{align*} x^2 - xy + y^2 - 2 &= 0\\ x+3y &= 4 \end{align*}$

51)$\begin{align*} x^2 - xy - 2y^2 - 6 &= 0\\ x^2 + y^2 &= 1 \end{align*}$

Responda: Não existe nenhuma solução

52)$\begin{align*} x^2 + 4xy - 2y^2 - 6 &= 0\\ x &= y+2 \end{align*}$

Tecnologia

Para os exercícios 53-54, resolva o sistema de desigualdades. Use uma calculadora para representar graficamente o sistema e confirmar a resposta.

53)$\begin{align*} xy &< 1\\ y &> \sqrt{x} \end{align*}$

Responda: $x=0$,$y>0$ e$0<1$>< span="">, $\sqrt{x} < y < \dfrac{1}{x}$/span>

54)$\begin{align*} x^2 + y &< 3\\ y &> 2x \end{align*}$

Aplicativos do mundo real

Para os exercícios 55-, construa um sistema de equações não lineares para descrever o comportamento dado e, em seguida, resolva as soluções solicitadas.

55) Dois números somam$300$. Um número é o dobro do quadrado do outro número. Quais são os números?

Responda: $12,288$

56) Os quadrados de dois números se somam$360$ a. O segundo número é metade do valor do primeiro número ao quadrado. Quais são os números?

57) Uma empresa de laptops descobriu suas funções de custo e receita para cada dia:$C(x)=3x^2-10x+200$$R(x)=-2x^2+100x+50$ e. Se eles querem lucrar, qual é a variedade de laptops por dia que eles devem produzir? Arredonde para o número mais próximo que geraria lucro.

Responda: $2$-$20$ computadores

58) Uma empresa de telefonia celular tem as seguintes funções de custo$C(x)=8x^2-600x+21,500$ e receita:$R(x)=-3x^2+480x$ e. Qual é a variedade de telefones celulares que eles devem produzir todos os dias para que haja lucro? Arredonde para o número mais próximo que gera lucro.

9.4: Frações parciais

Verbal

1) Qualquer quociente de polinômios pode ser decomposto em pelo menos duas frações parciais? Em caso afirmativo, explique por que, e se não, dê um exemplo dessa fração.

Responda: Não, um quociente de polinômios só pode ser decomposto se o denominador puder ser fatorado. Por exemplo,$\dfrac{1}{x^2+1}$ não pode ser decomposto porque o denominador não pode ser fatorado.

2) Você pode explicar por que uma decomposição parcial de frações é única? (Dica: pense nisso como um sistema de equações.)

3) Você pode explicar como verificar graficamente uma decomposição parcial de frações?

Responda: Faça um gráfico dos dois lados e verifique se eles são iguais.

4) Você não tem certeza se decompôs corretamente a fração parcial. Explique como você pode verificar sua resposta.

5) Depois de ter um sistema de equações gerado pela decomposição parcial da fração, você pode explicar outro método para resolvê-lo? Por exemplo, se você tivesse, eventualmente$\dfrac{7x+13}{3x^2+8x+15}=\dfrac{A}{x+1}+\dfrac{B}{3x+5}$ simplificamos para$7x+13=A(3x+5)+B(x+1)$. Explique como você pode escolher de forma inteligente um$x$ valor -que eliminará$A$ ou resolverá$B$$A$$B$ e.

Responda: Se escolhermos$x=-1$, então o$B$ termo -desaparece, informando-nos imediatamente disso$A=3$. Alternativamente, poderíamos conectar$x=-\dfrac{5}{3}$, nos dando um$B$ valor de -de$-2$.

Algébrico

Para os exercícios 6-19, determine a decomposição da fração parcial para os fatores lineares não repetidos.

6)$\dfrac{5x+16}{x^2+10x+24}$

7)$\dfrac{3x-79}{x^2-5x-24}$

Responda: $\dfrac{8}{x+3}-\dfrac{5}{x-8}$

8)$\dfrac{-x-24}{x^2-2x-24}$

9)$\dfrac{10x+47}{x^2+7x+10}$

Responda: $\dfrac{1}{x+5}+\dfrac{9}{x+2}$

10)$\dfrac{x}{6x^2+25x+25}$

11)$\dfrac{32x-11}{20x^2-13x+2}$

Responda: $\dfrac{3}{5x-2}+\dfrac{4}{4x-1}$

12)$\dfrac{x+1}{x^2+7x+10}$

13)$\dfrac{5x}{x^2-9}$

Responda: $\dfrac{5}{2(x+3)}+\dfrac{5}{2(x-3)}$

14)$\dfrac{10x}{x^2-25}$

15)$\dfrac{6x}{x^2-4}$

Responda: $\dfrac{3}{x+2}+\dfrac{3}{x-2}$

16)$\dfrac{2x-3}{x^2-6x+5}$

17)$\dfrac{4x-1}{x^2-x-6}$

Responda: $\dfrac{9}{5(x+2)}+\dfrac{11}{5(x-3)}$

18)$\dfrac{4x+3}{x^2+8x+15}$

19)$\dfrac{3x-1}{x^2-5x+6}$

Responda: $\dfrac{8}{x-3}-\dfrac{5}{x-2}$

Para os exercícios 20-30, determine a decomposição da fração parcial para os fatores lineares repetidos.

20)$\dfrac{-5x-19}{(x+4)^2}$

21)$\dfrac{x}{(x-2)^2}$

Responda: $\dfrac{1}{x-2}-\dfrac{2}{(x-2)^2}$

22)$\dfrac{7x+14}{(x+3)^2}$

23)$\dfrac{-24x-27}{(4x+5)^2}$

Responda: $-\dfrac{6}{4x+5}+\dfrac{3}{(4x+5)^2}$

24)$\dfrac{-24x-27}{(6x-7)^2}$

25)$\dfrac{5-x}{(x-7)^2}$

Responda: $-\dfrac{1}{x-7}-\dfrac{2}{(x-7)^2}$

26)$\dfrac{5x+14}{2x^2+12x+18}$

27)$\dfrac{5x^2+20x+8}{2x(x+1)^2}$

Responda: $\dfrac{4}{x}-\dfrac{3}{2(x+1)}+\dfrac{7}{2(x+1)^2}$

28)$\dfrac{4x^2+55x+25}{5x(3x+5)^2}$

29)$\dfrac{54x^3+127x^2+80x+16}{2x^2(3x+2)^2}$

Responda: $\dfrac{4}{x}+\dfrac{2}{x^2}-\dfrac{3}{3x+2}+\dfrac{7}{2(3x+2)^2}$

30)$\dfrac{x^3-5x^2+12x+144}{x^2(x^2+12x+36)}$

Para os exercícios 31-43, determine a decomposição da fração parcial para o fator quadrático irredutível e não repetitivo.

31)$\dfrac{4x^2+6x+11}{(x+2)(x^2+x+3)}$

Responda: $\dfrac{x+1}{x^2+x+3}+\dfrac{3}{(x+2)}$

32)$\dfrac{4x^2+9x+23}{(x-1)(x^2+6x+11)}$

33)$\dfrac{-2x^2+10x+4}{(x-1)(x^2+3x+8)}$

Responda: $\dfrac{4-3x}{x^2+3x+8}+\dfrac{1}{(x-1)}$

34)$\dfrac{x^2+3x+1}{(x+1)(x^2+5x-2)}$

(35)$\dfrac{4x^2+17x-1}{(x+3)(x^2+6x+1)}$

Responda: $\dfrac{2x-1}{x^2+6x+1}+\dfrac{2}{(x+3)}$

36)$\dfrac{4x^2}{(x+5)(x^2+7x-5)}$

37)$\dfrac{4x^2+x+3}{x^3 - 1}$

Responda: $\dfrac{1}{x^2+x+1}+\dfrac{4}{(x-1)}$

38)$\dfrac{-5x^2+18x-4}{x^3 + 8}$

39)$\dfrac{3x^2-7x+33}{x^3 + 27}$

Responda: $\dfrac{2}{x^2-3x+9}+\dfrac{3}{(x+3)}$

40)$\dfrac{x^2+2x+40}{x^3 - 125}$

41)$\dfrac{4x^2+4x+12}{8x^3 - 27}$

Responda: $-\dfrac{1}{4x^2+6x+9}+\dfrac{1}{(2x-3)}$

(42)$\dfrac{-50x^2+5x-3}{125x^3 - 1}$

43)$\dfrac{-2x^3-30x^2+36x+216}{x^4 + 216x}$

Responda: $\dfrac{1}{x}+\dfrac{1}{x+6}-\dfrac{4x}{x^2-6x+36}$

Para os exercícios 44-54, determine a decomposição da fração parcial para o fator quadrático repetitivo irredutível.

44)$\dfrac{3x^3+2x^2+14x+15}{(x^2 + 4)^2}$

45)$\dfrac{x^3+6x^2+5x+9}{(x^2 + 1)^2}$

Responda: $\dfrac{x+6}{x^2+1}+\dfrac{4x+3}{(x^2+1)^2}$

(46)$\dfrac{x^3-x^2+x-1}{(x^2 - 3)^2}$

47)$\dfrac{x^2+5x+5}{(x+2)^2}$

Responda: $\dfrac{x+1}{x+2}+\dfrac{2x+3}{(x+2)^2}$

48)$\dfrac{x^3+2x^2+4x}{(x^2+2x+9)^2}$

49)$\dfrac{x^2+25}{(x^2+3x+25)^2}$

Responda: $\dfrac{1}{x^2+3x+25}-\dfrac{3x}{(x^2+3x+25)^2}$

50)$\dfrac{2x^3+11x+7x+70}{(2x^2+x+14)^2}$

51)$\dfrac{5x+2}{x(x^2+4)^2}$

Responda: $\dfrac{1}{8x}-\dfrac{x}{8(x^2+4)}+\dfrac{10-x}{8(x^2+4)^2}$

52)$\dfrac{x^4+x^3+8x^2+6x+36}{x(x^2+6)^2}$

53)$\dfrac{2x-9}{(x^2-x)^2}$

Responda: $-\dfrac{16}{x}-\dfrac{9}{x^2}+\dfrac{16}{x-1}-\dfrac{7}{(x-1)^2}$

54)$\dfrac{5x^3-2x+1}{(x^2+2x)^2}$

Extensões

Para os exercícios 55-56, determine a expansão parcial da fração.

55)$\dfrac{x^2+4}{(x+1)^3}$

Responda: $\dfrac{1}{x+1}-\dfrac{2}{(x+1)^2}+\dfrac{5}{(x+1)^3}$

56)$\dfrac{x^3-4x^2+5x+4}{(x-2)^3}$

Para os exercícios 57-59, execute a operação e encontre a decomposição parcial da fração.

57)$\dfrac{7}{x+8}+\dfrac{5}{x-2}-\dfrac{x-1}{x^2-6x-16}$

Responda: $\dfrac{5}{x-2}-\dfrac{3}{10(x+2)}+\dfrac{7}{x+8}-\dfrac{7}{10(x-8)}$

(58)$\dfrac{1}{x-4}-\dfrac{3}{x+6}-\dfrac{2x+7}{x^2+2x-24}$

(59)$\dfrac{2x}{x^2-16}-\dfrac{1-2x}{x^2+6x+8}-\dfrac{x-5}{x^2-4x}$

Responda: $-\dfrac{5}{4x}-\dfrac{5}{2(x+2)}+\dfrac{11}{2(x+4)}+\dfrac{5}{4(x+4)}$

9.5: Matrizes e operações matriciais

Verbal

1) Podemos adicionar duas matrizes? Se sim, explique por que; se não, explique por que não e dê um exemplo de duas matrizes que não podem ser somadas.

Responda: Não, eles devem ter as mesmas dimensões. Um exemplo incluiria duas matrizes de dimensões diferentes. Não se pode adicionar as duas matrizes a seguir porque a primeira é uma$2\times 2$ matriz e a segunda é uma$2\times 3$. $\begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix} + \begin{bmatrix} 6 & 5 & 4\\ 3 & 2 & 1 \end{bmatrix}$não tem soma.

2) Podemos multiplicar qualquer matriz de coluna por qualquer matriz de linha? Explique por que ou por que não.

3) Tanto os produtos quanto os produtos$AB$$BA$ podem ser definidos? Se sim, explique como; se não, explique por quê.

Responda: Sim, se as dimensões de$A$ forem$m\times n$ e as dimensões de$B$ forem,$n\times m$ ambos os produtos serão definidos.

4) Duas matrizes do mesmo tamanho podem ser multiplicadas? Em caso afirmativo, explique por que e, se não, explique por que não e dê um exemplo de duas matrizes do mesmo tamanho que não podem ser multiplicadas juntas.

5) A multiplicação de matrizes se desloca? Ou seja, faz$AB=BA$? Se sim, prove por que isso acontece. Se não, explique por que isso não acontece.

Responda: Não necessariamente. Para encontrar$AB$, multiplicamos a primeira linha de$A$ pela primeira coluna de$B$ para obter a primeira entrada de$AB$. Para encontrar$BA$, multiplicamos a primeira linha de$B$ pela primeira coluna de$A$ para obter a primeira entrada de$BA$. Assim, se esses forem desiguais, a multiplicação da matriz não se desloca.

Algébrico

Para os exercícios 6-11, use as matrizes abaixo e realize a adição ou subtração da matriz. Indique se a operação está indefinida.

\[A=\begin{bmatrix} 1 & 3\\ 0 & 7 \end{bmatrix}, B=\begin{bmatrix} 2 & 14\\ 22 & 6 \end{bmatrix}, C=\begin{bmatrix} 1 & 5\\ 8 & 92\\ 12 & 6 \end{bmatrix}, D=\begin{bmatrix} 10 & 14\\ 7 & 2\\ 5 & 61 \end{bmatrix}, E=\begin{bmatrix} 6 & 12\\ 14 & 5 \end{bmatrix}, F=\begin{bmatrix} 0 & 9\\ 78 & 17\\ 15 & 4 \end{bmatrix} \nonumber\]

6)$A+B$

7)$C+D$

Responda: $\begin{bmatrix} 11 & 19\\ 15 & 94\\ 17 & 67 \end{bmatrix}$

8)$A+C$

9)$B-E$

Responda: $\begin{bmatrix} -4 & 2\\ 8 & 1 \end{bmatrix}$

10)$C+F$

11)$D-B$

Responda: Indefinido; as dimensões não coincidem

Para os exercícios 12-17, use as matrizes abaixo para realizar a multiplicação escalar.

\[A=\begin{bmatrix} 4 & 6\\ 13 & 12 \end{bmatrix}, B=\begin{bmatrix} 3 & 9\\ 21 & 12\\ 0 & 64 \end{bmatrix}, C=\begin{bmatrix} 16 & 3 & 7 & 18\\ 90 & 5 & 3 & 29 \end{bmatrix}, D=\begin{bmatrix} 18 & 12 & 13\\ 8 & 14 & 6\\ 7 & 4 & 21 \end{bmatrix} \nonumber\]

12)$5A$

13)$3B$

Responda: $\begin{bmatrix} 9 & 27\\ 63 & 36\\ 0 & 192 \end{bmatrix}$

14)$-2B$

15)$-4C$

Responda: $\begin{bmatrix} -64 & -12 & -28 & -72\\ -360 & -20 & -12 & -116 \end{bmatrix}$

16)$\dfrac{1}{2}C$

17)$100D$

Responda: $\begin{bmatrix} 1,800 & 1,200 & 1,300\\ 800 & 1,400 & 600\\ 700 & 400 & 2,100 \end{bmatrix}$

Para os exercícios 18-23, use as matrizes abaixo para realizar a multiplicação de matrizes.

\[A=\begin{bmatrix} -1 & 5\\ 3 & 2 \end{bmatrix}, B=\begin{bmatrix} 3 & 6 & 4\\ -8 & 0 & 12 \end{bmatrix}, C=\begin{bmatrix} 4 & 10\\ -2 & 6\\ 5 & 9 \end{bmatrix}, D=\begin{bmatrix} 2 & -3 & 12\\ 9 & 3 & 1\\ 0 & 8 & -10 \end{bmatrix} \nonumber\]

18)$AB$

19)$BC$

Responda: $\begin{bmatrix} 20 & 102\\ 28 & 28 \end{bmatrix}$

20)$CA$

21)$BD$

Responda: $\begin{bmatrix} 60 & 41 & 2\\ -16 & 120 & -216 \end{bmatrix}$

22)$DC$

23)$CB$

Responda: $\begin{bmatrix} -68 & 24 & 136\\ -54 & -12 & 64\\ -57 & 30 & 128 \end{bmatrix}$

Para os exercícios 24-29, use as matrizes abaixo para realizar a operação indicada, se possível. Se não for possível, explique por que a operação não pode ser executada.

\[A=\begin{bmatrix} 2 & -5\\ 6 & 7 \end{bmatrix}, B=\begin{bmatrix} -9 & 6\\ -4 & 2 \end{bmatrix}, C=\begin{bmatrix} 0 & 9\\ 7 & 1 \end{bmatrix}, D=\begin{bmatrix} -8 & 7 & -5\\ 4 & 3 & 2\\ 0 & 9 & 2 \end{bmatrix}, E=\begin{bmatrix} 4 & 5 & 3\\ 7 & -6 & -5\\ 1 & 0 & 9 \end{bmatrix} \nonumber\]

24)$A+B-C$

25)$4A+5D$

Responda: Indefinido; as dimensões não coincidem.

26)$2C+B$

27)$3D+4E$

Responda: $\begin{bmatrix} -8 & 41 & -3\\ 40 & -15 & -14\\ 4 & 27 & 42 \end{bmatrix}$

28)$C-0.5D$

29)$100D-10E$

Responda: $\begin{bmatrix} -840 & 650 & -530\\ 330 & 360 & 250\\ -10 & 900 & 110 \end{bmatrix}$

Para os exercícios 30-40, use as matrizes abaixo para realizar a operação indicada, se possível. Se não for possível, explique por que a operação não pode ser executada. (Dica:$A^2=A\cdot A$)

\[A=\begin{bmatrix} -10 & 20\\ 5 & 25 \end{bmatrix}, B=\begin{bmatrix} 40 & 10\\ -20 & 30 \end{bmatrix}, C=\begin{bmatrix} -1 & 0\\ 0 & -1\\ 1 & 0 \end{bmatrix} \nonumber\]

30)$AB$

31)$BA$

Responda: $\begin{bmatrix} -350 & 1,050\\ 350 & 350 \end{bmatrix}$

32)$CA$

33)$BC$

Responda: Indefinido; as dimensões internas não coincidem.

34)$A^2$

(35)$B^2$

Responda: $\begin{bmatrix} 1,400 & 700\\ -1,400 & 700 \end{bmatrix}$

36)$C^2$

37)$B^2A^2$

Responda: $\begin{bmatrix} 332,500 & 927,500\\ -227,500 & 87,500 \end{bmatrix}$

38)$A^2B^2$

39)$(AB)^2$

Responda: $\begin{bmatrix} 490,000 & 0\\ 0 & 490,000 \end{bmatrix}$

40)$(BA)^2$

Para os exercícios 41-49, use as matrizes abaixo para realizar a operação indicada, se possível. Se não for possível, explique por que a operação não pode ser executada. (Dica:$A^2=A\cdot A$)

\[A=\begin{bmatrix} 1 & 0\\ 2 & 3 \end{bmatrix}, B=\begin{bmatrix} -2 & 3 & 4\\ -1 & 1 & -5 \end{bmatrix}, C=\begin{bmatrix} 0.5 & 0.1\\ 1 & 0.2\\ -0.5 & 0.3 \end{bmatrix}, D=\begin{bmatrix} 1 & 0 & -1\\ -6 & 7 & 5\\ 4 & 2 & 1 \end{bmatrix} \nonumber\]

41)$AB$

Responda: $\begin{bmatrix} -2 & 3 & 4\\ -7 & 9 & -7 \end{bmatrix} \nonumber$

(42)$BA$

43)$BD$

Responda: $\begin{bmatrix} -4 & 29 & 21\\ -27 & -3 & 1 \end{bmatrix} \nonumber$

44)$DC$

45)$D^2$

Responda: $\begin{bmatrix} -3 & -2 & -2\\ -28 & 59 & 46\\ -4 & 16 & 7 \end{bmatrix} \nonumber$

(46)$A^2$

47)$D^3$

Responda: $\begin{bmatrix} 1 & -18 & -9\\ -198 & 505 & 369\\ -72 & 126 & 91 \end{bmatrix} \nonumber$

48)$(AB)C$

49)$A(BC)$

Responda: $\begin{bmatrix} 0 & 1.6\\ 9 & -1 \end{bmatrix} \nonumber$

Tecnologia

Para os exercícios 50-54, use as matrizes abaixo para realizar a operação indicada, se possível. Se não for possível, explique por que a operação não pode ser executada. Use uma calculadora para verificar sua solução.

\[A=\begin{bmatrix} -2 & 0 & 9\\ 1 & 8 & -3\\ 0.5 & 4 & 5 \end{bmatrix}, B=\begin{bmatrix} 0.5 & 3 & 0\\ -4 & 1 & 6\\ 8 & 7 & 2 \end{bmatrix}, C=\begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & 0\\ 1 & 0 & 1 \end{bmatrix} \nonumber\]

50)$AB$

51)$BA$

Responda: $\begin{bmatrix} 2 & 24 & -4.5\\ 12 & 32 & -9\\ -8 & 64 & 61 \end{bmatrix} \nonumber$

52)$CA$

53)$BC$

Responda: $\begin{bmatrix} 0.5 & 3 & 0.5\\ 2 & 1 & 2\\ 10 & 7 & 10 \end{bmatrix} \nonumber$

54)$ABC$

Extensões

Para os exercícios 55-, use a matriz abaixo para realizar a operação indicada na matriz dada.

\[B=\begin{bmatrix} 1 & 0 & 0\\ 0 & 0 & 1\\ 0 & 1 & 0 \end{bmatrix} \nonumber\]

55)$B^2$

Responda: $\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix} \nonumber$

(56)$B^3$

57)$B^4$

Responda: $\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix} \nonumber$

(58)$B^5$

59) Usando as perguntas acima, encontre uma fórmula para$B^n$. Teste a fórmula para$B^{201}$ e$B^{202}$, usando uma calculadora.

Responda: $B^n=\begin{cases} \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}, & n\text{ even }\\ \\ \begin{bmatrix} 1 & 0 & 0\\ 0 & 0 & 1\\ 0 & 1 & 0 \end{bmatrix}, & n\text{ odd } \end{cases}$

9.6: Resolvendo sistemas com eliminação gaussiana

Verbal

1) Qualquer sistema de equações lineares pode ser escrito como uma matriz aumentada? Explique por que ou por que não. Explique como escrever essa matriz aumentada.

Responda: Sim. Para cada linha, os coeficientes das variáveis são escritos na linha correspondente e uma barra vertical é colocada; em seguida, as constantes são colocadas à direita da barra vertical.

2) Qualquer matriz pode ser escrita como um sistema de equações lineares? Explique por que ou por que não. Explique como escrever esse sistema de equações.

3) Existe apenas um método correto de usar operações de linha em uma matriz? Tente explicar duas operações de linha diferentes possíveis para resolver a matriz aumentada$\left [ \begin{array}{cc|c} 9 & 3 & 0\\ 1 & -2 & 6\\ \end{array} \right ]$.

Responda

Não, existem vários métodos corretos de usar operações de linha em uma matriz. Duas formas possíveis são as seguintes:

Troque as linhas 1 e 2. Então$R_2=R_2-9R_1$.
$R_2=R_1-9R_2$. Em seguida, divida a linha 1 por$9$.

4) Uma matriz cuja entrada está$0$ na diagonal pode ser resolvida? Explique por que ou por que não. O que você faria para remediar a situação?

5) Uma matriz com$0$ entradas para uma linha inteira pode ter uma solução? Explique por que ou por que não.

Responda: Não. Uma matriz com$0$ entradas para uma linha inteira teria zero ou infinitas soluções.

Algébrico

Para os exercícios 6-10, escreva a matriz aumentada para o sistema linear.

6)$\begin{align*} 8x-37y &= 8\\ 2x+12y &= 3 \end{align*}$

7)$\begin{align*} 16y &= 4\\ 9x-y &= 2 \end{align*}$

Responda: $\left [ \begin{array}{cc|c} 0 & 16 & 4\\ 9 & -1 & 2\\ \end{array} \right ]$

8)$\begin{align*} 3x+2y+10z &= 3\\ -6x+2y+5z &= 13\\ 4x+z &= 18 \end{align*}$

9)$\begin{align*} x+5y+8z &= 19\\ 12x+3y &= 4\\ 3x+4y+9z &= -7 \end{align*}$

Responda: $\left [ \begin{array}{ccc|c} 1 & 5 & 8 & 16\\ 12 & 3 & 0 & 4\\ 3 & 4 & 9 & -7\end{array} \right ]$

10)$\begin{align*} 6x+12y+16z &= 4\\ 19x-5y+3z &= -9\\ x+2y &= -8 \end{align*}$

Para os exercícios 11-15, escreva o sistema linear a partir da matriz aumentada.

11)$\left [ \begin{array}{cc|c} -2 & 5 & 5\\ 6 & -18 & 26\\ \end{array} \right ]$

Responda: $\begin{align*} -2x+5y &= 5\\ 6x-18y &= 26 \end{align*}$

12)$\left [ \begin{array}{cc|c} 3 & 4 & 10\\ 10 & 17 & 439\\ \end{array} \right ]$

13)$\left [ \begin{array}{ccc|c} 3 & 2 & 0 & 3\\ -1 & -9 & 4& -1\\ 8 & 5 & 7 & 8\\ \end{array} \right ]$

Responda: $\begin{align*} 3x+2y &= 13\\ -x-9y+4z &= 53\\ 8x+5y+7z &= 80 \end{align*}$

14)$\left [ \begin{array}{ccc|c} 8 & 29 & 1 & 43\\ -1 & 7 & 5 & 38\\ 0 & 0 & 3 & 10\\ \end{array} \right ]$

15)$\left [ \begin{array}{ccc|c} 4 & 5 & -2 & 12\\ 0 & 1 & 58 & 2\\ 8 & 7 & -3 & -5\\ \end{array} \right ]$

Responda: $\begin{align*} 4x+5y-2z &= 12\\ y+58z &= 2\\ 8x+7y-3z &= -5 \end{align*}$

Para os exercícios 16-46, resolva o sistema por eliminação gaussiana.

16)$\left [ \begin{array}{cc|c} 1 & 0 & 3\\ 0 & 0 & 0\\ \end{array} \right ]$

17)$\left [ \begin{array}{cc|c} 1 & 0 & 1\\ 1 & 0 & 2\\ \end{array} \right ]$

Responda: Sem soluções

18)$\left [ \begin{array}{cc|c} 1 & 2 & 3\\ 4 & 5 & 6\\ \end{array} \right ]$

19)$\left [ \begin{array}{cc|c} -1 & 2 & -3\\ 4 & -5 & 6\\ \end{array} \right ]$

Responda: $(-1,-2)$

20)$\left [ \begin{array}{cc|c} -2 & 0 & 1\\ 0 & 2 & -1\\ \end{array} \right ]$

21)$\begin{align*} 2x-3y &= -9\\ 5x+4y &= 58 \end{align*}$

Responda: $(6,7)$

22)$\begin{align*} 6x+2y &= -4\\ 3x+4y &= -17 \end{align*}$

23)$\begin{align*} 2x+3y &= 12\\ 4x+y &= 14 \end{align*}$

Responda: $(3,2)$

24)$\begin{align*} -4x-3y &= -2\\ 3x-5y &= -13 \end{align*}$

25)$\begin{align*} -5x+8y &= 3\\ 10x+6y &= 5 \end{align*}$

Responda: $\left (\dfrac{1}{5}, \dfrac{1}{2} \right )$

26)$\begin{align*} 3x+4y &= 12\\ -6x-8y &= -24 \end{align*}$

27)$\begin{align*} -60x+45y &= 12\\ 20x-15y &= -4 \end{align*}$

Responda: $\left (x, \dfrac{4}{15}(5x+1) \right )$

28)$\begin{align*} 11x+10y &= 43\\ 15x+20y &= 65 \end{align*}$

29)$\begin{align*} 2x-y &= 2\\ 3x+2y &= 17 \end{align*}$

Responda: $(3,4)$

30)$\begin{align*} -1.06x-2.25y &= 5.51\\ -5.03x-1.08y &= 5.40 \end{align*}$

31)$\begin{align*} \dfrac{3}{4}x-\dfrac{3}{5}y &= 4\\ \dfrac{1}{4}x+\dfrac{2}{3}y &= 1 \end{align*}$

Responda: $\left (\dfrac{196}{39}, -\dfrac{5}{13} \right )$

32)$\begin{align*} \dfrac{1}{4}x-\dfrac{2}{3}y &= -1\\ \dfrac{1}{2}x+\dfrac{1}{3}y &= 3 \end{align*}$

33)$\left [ \begin{array}{ccc|c} 1 & 0 & 0 & 31\\ 0 & 1 & 1 & 45\\ 0 & 0 & 1 & 87\\ \end{array} \right ]$

Responda: $(31,-42,87)$

34)$\left [ \begin{array}{ccc|c} 1 & 0 & 1 & 50\\ 1 & 1 & 0 & 20\\ 0 & 1 & 1 & -90\\ \end{array} \right ]$

(35)$\left [ \begin{array}{ccc|c} 1 & 2 & 3 & 4\\ 0 & 5 & 6 & 7\\ 0 & 0 & 8 & 9\\ \end{array} \right ]$

Responda: $\left (\dfrac{21}{40}, \dfrac{1}{20}, \dfrac{9}{8} \right )$

36)$\left [ \begin{array}{ccc|c} -0.1 & 0.3 & -0.1 & 0.2\\ -0.4 & 0.2 & 0.1 & 0.8\\ 0.6 & 0.1 & 0.7 & -0.8\\ \end{array} \right ]$

37)$\begin{align*} -2x+3y-2z &= 3\\ 4x+2y-z &= 9\\ 4x-8y+2z &= -6 \end{align*}$

Responda: $\left (\dfrac{18}{13}, \dfrac{15}{13}, -\dfrac{15}{13} \right )$

38)$\begin{align*} x+y-4z &= -4\\ 5x-3y-2z &= 0\\ 2x+6y+7z &= 30 \end{align*}$

39)$\begin{align*} 2x+3y+2z &= 1\\ -4x-6y-4z &= -2\\ 10x+15y+10z &= 5 \end{align*}$

Responda: $\left (x, y, \dfrac{1}{2}(1-2x-3y) \right )$

40)$\begin{align*} x+2y-z &= 1\\ -x-2y+2z &= -2\\ 3x+6y-3z &= 5 \end{align*}$

41)$\begin{align*} x+2y-z &= 1\\ -x-2y+2z &= -2\\ 3x+6y-3z &= 3 \end{align*}$

Responda: $\left (x, -\dfrac{x}{2}, -1 \right )$

(42)$\begin{align*} x+y &= 2\\ x+z &= 1\\ -y-z &= -3 \end{align*}$

43)$\begin{align*} x+y+z &= 100\\ x+2z &= 125\\ -y+2z &= 25 \end{align*}$

Responda: $(125,-25,0)$

44)$\begin{align*} \dfrac{1}{4}x-\dfrac{2}{3}z &= -\dfrac{1}{2}\\ \dfrac{1}{5}x+\dfrac{1}{3}y &= \dfrac{4}{7}\\ \dfrac{1}{5}y-\dfrac{1}{3}z &= \dfrac{2}{9} \end{align*}$

45)$\begin{align*} -\dfrac{1}{2}x+\dfrac{1}{2}y+\dfrac{1}{7}z &= -\dfrac{53}{14}\\ \dfrac{1}{2}x-\dfrac{1}{2}y+\dfrac{1}{4}z &= 3\\ \dfrac{1}{4}x+\dfrac{1}{5}y+\dfrac{1}{3}z &= \dfrac{23}{15} \end{align*}$

Responda: $(8,1,-2)$

(46)$\begin{align*} -\dfrac{1}{2}x-\dfrac{1}{3}y+\dfrac{1}{4}z &= -\dfrac{29}{6}\\ \dfrac{1}{5}x+\dfrac{1}{6}y-\dfrac{1}{7}z &= \dfrac{431}{210}\\ -\dfrac{1}{8}x+\dfrac{1}{9}y+\dfrac{1}{10}z &= -\dfrac{49}{45} \end{align*}$

Extensões

Para os exercícios 47-51, use a eliminação gaussiana para resolver o sistema.

47)$\begin{align*} \dfrac{x-1}{7}+\dfrac{y-2}{8}+\dfrac{z-3}{4} &= 0\\ x+y+z &= 6\\ \dfrac{x+2}{3}+2y+\dfrac{z-3}{3} &= 5 \end{align*}$

Responda: $(1,2,3)$

48)$\begin{align*} \dfrac{x-1}{4}-\dfrac{y+1}{4}+3z &= -1\\ \dfrac{x+5}{2}+\dfrac{y+7}{4}-z &= 4\\ x+y-\dfrac{z-2}{2} &= 1 \end{align*}$

49)$\begin{align*} \dfrac{x-3}{4}-\dfrac{y-1}{3}+2z &= -1\\ \dfrac{x+5}{2}+\dfrac{y+5}{2}+\dfrac{z+5}{2} &= 8\\ x+y+z &= 1 \end{align*}$

Responda: $\left (x, \dfrac{31}{28}-\dfrac{3x}{4}, \dfrac{1}{28}(-7x-3) \right )$

50)$\begin{align*} \dfrac{x-3}{10}+\dfrac{y+3}{2}-2z &= 3\\ \dfrac{x+5}{4}-\dfrac{y-1}{8}+z &= \dfrac{3}{2}\\ \dfrac{x-1}{4}+\dfrac{y+4}{2}+3z &= \dfrac{3}{2} \end{align*}$

51)$\begin{align*} \dfrac{x-3}{4}-\dfrac{y-1}{3}+2z &= -1\\ \dfrac{x+5}{2}+\dfrac{y+5}{2}+\dfrac{z+5}{2} &= 7\\ x+y+z &= 1 \end{align*}$

Responda: Não existem soluções.

Aplicativos do mundo real

Para os exercícios 52-61, configure a matriz aumentada que descreve a situação e resolva a solução desejada.

52) Todos os dias, uma loja de cupcakes vende$5,000$ cupcakes nos sabores de chocolate e baunilha. Se o sabor do chocolate$3$ é tão popular quanto o sabor de baunilha, quantos cupcakes são vendidos por dia?

53) Em uma loja de cupcakes concorrente, cupcakes$\$4,520$ valiosos são vendidos diariamente. Os cupcakes de chocolate custam$\$2.25$ e os cupcakes de veludo vermelho custam$\$1.75$. Se o número total de cupcakes vendidos por dia for$2,200$, quantos de cada sabor são vendidos por dia?

Responda: $860$veludo vermelho,$1,340$ chocolate

54) Você$\$10,000$ investiu em duas contas: uma com$3\%$ juros simples e outra com$2.5\%$ juros. Se o pagamento total de juros após um ano foi$\$283.50$, quanto estava em cada conta após o término do ano?

55) Você investiu$\$2,300$ na conta 1 e$\$2,700$ na conta 2. Se o valor total dos juros após um ano for$\$254$, e a conta 2 tiver$1.5$ vezes a taxa de juros da conta 1, quais são as taxas de juros? Suponha taxas de juros simples.

Responda: $4\%$para a conta 1,$6\%$ para a conta 2

56) A Bikes'R'Us fabrica bicicletas, que são vendidas por$\$250$. Custa ao fabricante$\$180$ por bicicleta, além de uma taxa inicial de$\$3,500$. Depois de quantas bicicletas vendidas, o fabricante empatará?

57) Uma grande loja de eletrodomésticos está considerando comprar aspiradores de um pequeno fabricante. A loja seria capaz de comprar os aspiradores para$\$86$ cada um, com uma taxa de entrega de$\$9,200$, independentemente de quantos aspiradores sejam vendidos. Se a loja precisar começar a lucrar após a venda$230$ das unidades, quanto ela deve cobrar pelos aspiradores?

Responda: $\$126$

58) Os três sabores de sorvete mais populares são chocolate, morango e baunilha, compostos pelos$83\%$ sabores vendidos em uma sorveteria. Se a baunilha vende$1\%$ mais do que o dobro de morango e o chocolate vende$11\%$ mais do que a baunilha, quanto do consumo total de sorvete são os sabores de baunilha, chocolate e morango?

59) Em uma sorveteria, a demanda por três sabores está aumentando. No ano passado, sorvetes de banana, abóbora e estrada rochosa representaram as vendas totais$12\%$ de sorvetes. Este ano, os mesmos três sorvetes foram compostos pela venda$16.9\%$ de sorvetes. As vendas em estradas rochosas dobraram, as vendas de bananas$50\%$ aumentaram e as vendas de abóbora aumentaram$20\%$. Se o sorvete Rocky Road teve um por cento a menos das vendas do que o sorvete de banana, descubra a porcentagem de vendas de sorvete que cada sorvete fez no ano passado.

Responda: Banana era$3\%$, abóbora era$7\%$ e estrada rochosa era$2\%$

60) Um saco de nozes misturadas contém castanha de caju, pistache e amêndoas. Há$1,000$ um total de nozes na sacola e há$100$ menos amêndoas do que pistache. Os cajus pesam$3$ g, os pistaches pesam$4$ g e as amêndoas pesam$5$ g. Se o saco pesar$3.7$ kg, descubra quantas nozes de cada tipo estão na sacola.

61) Um saco de nozes misturadas contém castanha de caju, pistache e amêndoas. Originalmente, havia$900$ nozes na sacola. $30\%$das amêndoas,$20\%$ dos cajus e$10\%$ dos pistaches foram comidos, e agora sobram$770$ nozes na sacola. Originalmente, havia$100$ mais cajus do que amêndoas. Para começar, descubra quantas nozes de cada tipo estavam na sacola.

Responda: $100$amêndoas,$200$ castanha de caju,$600$ pistache

9.7: Resolvendo sistemas com inversas

Verbal

1) Em uma seção anterior, mostramos que a multiplicação de matrizes não é comutativa, ou seja,$AB\neq BA$ na maioria dos casos. Você pode explicar por que a multiplicação de matrizes é comutativa para inversos de matrizes, ou seja,$A^{-1}A=AA^{-1}$?

Responda: Se$A^{-1}$ for o inverso de$A$, então$AA^{-1}=I$, a matriz de identidade. Uma vez que também$A$ é o inverso de$A^{-1}$,$A^{-1}A=I$. Você também pode verificar provando isso para uma$2\times 2$ matriz.

2) Cada$2\times 2$ matriz tem um inverso? Explique por que ou por que não. Explique qual condição é necessária para que uma inversa exista.

3) Você pode explicar se uma$2\times 2$ matriz com uma linha inteira de zeros pode ter um inverso?

Responda: Não, porque$ad$ e$bc$ são ambos$0$, então$ad-bc=0$, o que exige que dividimos por$0$ na fórmula.

4) Uma matriz com uma coluna inteira de zeros pode ter um inverso? Explique por que ou por que não.

5) Uma matriz com zeros na diagonal pode ter um inverso? Se sim, encontre um exemplo. Se não, prove por que não. Para simplificar, suponha uma$2\times 2$ matriz.

Responda

Sim. Considere a matriz$\begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix}$. O inverso é encontrado com o seguinte cálculo:

$A^{-1} = \dfrac{1}{0(0)-1(1)} \begin{bmatrix} 0 & -1\\ -1 & 0 \end{bmatrix} = \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix}$

Algébrico

Nos exercícios 6-12, mostre que a matriz$A$ é o inverso da matriz$B$.

6)$A = \begin{bmatrix} 1 & 0\\ -1 & 1 \end{bmatrix}, B = \begin{bmatrix} 1 & 0\\ 1 & 1 \end{bmatrix}$

7)$A = \begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix}, B = \begin{bmatrix} -2 & 1\\ \frac{3}{2} & -\frac{1}{2} \end{bmatrix}$

Responda: $AB = BA = \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} = I$

8)$A = \begin{bmatrix} 4 & 5\\ 7 & 0 \end{bmatrix}, B = \begin{bmatrix} 0 & \frac{1}{7}\\ \frac{1}{5} & -\frac{4}{35} \end{bmatrix}$

9)$A = \begin{bmatrix} -2 & \frac{1}{2}\\ 3 & -1 \end{bmatrix}, B = \begin{bmatrix} -2 & -1\\ -6 & -4 \end{bmatrix}$

Responda: $AB = BA = \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} = I$

10)$A = \begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & -1\\ 0 & 1 & 1 \end{bmatrix}, B = \dfrac{1}{2}\begin{bmatrix} 2 & 1 & -1\\ 0 & 1 & 1\\ 0 & -1 & 1 \end{bmatrix}$

11)$A = \begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & -1\\ 0 & 1 & 1 \end{bmatrix}, B = \dfrac{1}{2}\begin{bmatrix} 2 & 1 & -1\\ 0 & 1 & 1\\ 0 & -1 & 1 \end{bmatrix}$

Responda: $AB = BA = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = I$

12)$A = \begin{bmatrix} 3 & 8 & 2\\ 1 & 1 & 1\\ 5 & 6 & 12 \end{bmatrix}, B = \dfrac{1}{36}\begin{bmatrix} -6 & 84 & -6\\ 7 & -26 & 1\\ -1 & -22 & 5 \end{bmatrix}$

Para os exercícios 13-26, determine o inverso multiplicativo de cada matriz, se ela existir.

13)$\begin{bmatrix} 3 & -2\\ 1 & 9 \end{bmatrix}$

Responda: $\dfrac{1}{29}\begin{bmatrix} 9 & 2\\ -1 & 3 \end{bmatrix}$

14)$\begin{bmatrix} -2 & 2\\ 3 & 1 \end{bmatrix}$

15)$\begin{bmatrix} -3 & 7\\ 9 & 2 \end{bmatrix}$

Responda: $\dfrac{1}{69}\begin{bmatrix} -2 & 7\\ 9 & 3 \end{bmatrix}$

16)$\begin{bmatrix} -4 & -3\\ -5 & 8 \end{bmatrix}$

17)$\begin{bmatrix} 1 & 1\\ 2 & 2 \end{bmatrix}$

Responda: Não há inverso

18)$\begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix}$

19)$\begin{bmatrix} 0.5 & 1.5\\ 1 & -0.5 \end{bmatrix}$

Responda: $\dfrac{4}{7}\begin{bmatrix} 0.5 & 1.5\\ 1 & -0.5 \end{bmatrix}$

20)$\begin{bmatrix} 1 & 0 & 6\\ -2 & 1 & 7\\ 3 & 0 & 2 \end{bmatrix}$

21)$\begin{bmatrix} 0 & 1 & -3\\ 4 & 1 & 0\\ 1 & 0 & 5 \end{bmatrix}$

Responda: $\dfrac{1}{17}\begin{bmatrix} -5 & 5 & -3\\ 20 & -3 & 12\\ 1 & -1 & 4 \end{bmatrix}$

22)$\begin{bmatrix} 1 & 2 & -1\\ -3 & 4 & 1\\ -2 & -4 & -5 \end{bmatrix}$

23)$\begin{bmatrix} 1 & 9 & -3\\ 2 & 5 & 6\\ 4 & -2 & -7 \end{bmatrix}$

Responda: $\dfrac{1}{209}\begin{bmatrix} 47 & -57 & 69\\ 10 & 19 & -12\\ -24 & 38 & -13 \end{bmatrix}$

24)$\begin{bmatrix} 1 & -2 & 3\\ -4 & 8 & -12\\ 1 & 4 & 2 \end{bmatrix}$

25)$\begin{bmatrix} \frac{1}{2} & \frac{1}{2} & \frac{1}{2}\\ \frac{1}{3} & \frac{1}{4} & \frac{1}{5}\\ \frac{1}{6} & \frac{1}{7} & \frac{1}{8} \end{bmatrix}$

Responda: $\begin{bmatrix} 18 & 60 & -168\\ -56 & -140 & 448\\ 40 & 80 & -280 \end{bmatrix}$

26)$\begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix}$

Para os exercícios 27-34, resolva o sistema usando o inverso de uma$2\times 2$ matriz.

27)$\begin{align*} 5x-6y &= -61\\ 4x+3y &= -2 \end{align*}$

Responda: $(-5,6)$

28)$\begin{align*} 8x+4y &= -100\\ 3x-4y &= 1 \end{align*}$

29)$\begin{align*} 3x-2y &= 6\\ -x+5y &= -2 \end{align*}$

Responda: $(2,0)$

30)$\begin{align*} 5x-4y &= -5\\ 4x+y &= 2.3 \end{align*}$

31)$\begin{align*} -3x-4y &= 9\\ 12x+4y &= -6 \end{align*}$

Responda: $\left (\dfrac{1}{3}, -\dfrac{5}{2} \right )$

32)$\begin{align*} -2x+3y &= \dfrac{3}{10}\\ -x+5y &= \dfrac{1}{2} \end{align*}$

33)$\begin{align*} \dfrac{8}{5}x-\dfrac{4}{5}y &= \dfrac{2}{5}\\ -\dfrac{8}{5}x+\dfrac{1}{5}y &= \dfrac{7}{10} \end{align*}$

Responda: $\left (-\dfrac{2}{3}, -\dfrac{11}{6} \right )$

34)$\begin{align*} \dfrac{1}{2}x+\dfrac{1}{5}y &= -\dfrac{1}{4}\\ \dfrac{1}{2}x-\dfrac{3}{5}y &= -\dfrac{9}{4} \end{align*}$

Para os exercícios 35-42, resolva um sistema usando o inverso de uma$3\times 3$ matriz.

(35)$\begin{align*} 3x-2y+5z &= 21\\ 5x+4y &= 37\\ x-2y-5z &= 5 \end{align*}$

Responda: $\left (7, \dfrac{1}{2}, \dfrac{1}{5} \right )$

36)$\begin{align*} 4x+4y+4z &= 40\\ 2x-3y+4z &= -12\\ -x+3y+4z &= 9 \end{align*}$

37)$\begin{align*} 6x-5y-z &= 31\\ -x+2y+z &= -6\\ 3x+3y+2z &= 13 \end{align*}$

Responda: $(5,0,-1)$

38)$\begin{align*} 6x-5y+2z &= -4\\ 2x+5y-z &= 12\\ 2x+5y+z &= 12 \end{align*}$

39)$\begin{align*} 4x-2y+3z &= -12\\ 2x+2y-9z &= 33\\ 6y-4z &= 1 \end{align*}$

Responda: $\dfrac{1}{34} \left(-35, -97, -154 \right)$

40)$\begin{align*} \dfrac{1}{10}x-\dfrac{1}{5}y+4z &= \dfrac{-41}{2}\\ \dfrac{1}{5}x-20y+\dfrac{2}{5}z &= -101\\ \dfrac{3}{10}x+4y-\dfrac{3}{10}z &= 23 \end{align*}$

41)$\begin{align*} \dfrac{1}{2}x-\dfrac{1}{5}y+\dfrac{1}{5}z &= \dfrac{31}{100}\\ -\dfrac{3}{4}x-\dfrac{1}{4}y+\dfrac{1}{2}z &= \dfrac{7}{40}\\ -\dfrac{4}{5}x-\dfrac{1}{2}y+\dfrac{3}{2}z &= \dfrac{1}{4} \end{align*}$

Responda: $\dfrac{1}{690} \left(65, -1136, -229 \right)$

(42)$\begin{align*} 0.1x+0.2y+0.3z &= -1.4\\ 0.1x-0.2y+0.3z &= 0.6\\ 0.4y+0.9z &= -2 \end{align*}$

Tecnologia

Para os exercícios 43-46, use uma calculadora para resolver o sistema de equações com matrizes inversas.

43)$\begin{align*} 2x-y &= -3\\ -x+2y &= 2.3\\ \end{align*}$

Responda: $\left (-\dfrac{37}{30}, \dfrac{8}{15} \right )$

44)$\begin{align*} -\dfrac{1}{2}x-\dfrac{3}{2}y &= -\dfrac{43}{20}\\ \dfrac{5}{2}x+\dfrac{11}{5}y &= \dfrac{31}{4}\\ \end{align*}$

45)$\begin{align*} 12.3x-2y-2.5z &= 2\\ 36.9x+7y-7.5z &= -7\\ 8y-5z &= -10 \end{align*}$

Responda: $\left (\dfrac{10}{123}, -1, \dfrac{2}{5} \right )$

(46)$\begin{align*} 0.5x-3y+6z &= -0.8\\ 0.7x-2y &= -0.06\\ 0.5x+4y+5z &= 0 \end{align*}$

Extensões

Para os exercícios 47-51, determine o inverso da matriz dada.

47)$\begin{bmatrix} 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1\\ 0 & 1 & 1 & 0\\ 0 & 0 & 1 & 1 \end{bmatrix}$

Responda: $\dfrac{1}{2}\begin{bmatrix} 2 & 1 & -1 & -1\\ 0 & 1 & 1 & -1\\ 0 & -1 & 1 & 1\\ 0 & 1 & -1 & 1 \end{bmatrix}$

48)$\begin{bmatrix} -1 & 0 & 2 & 5\\ 0 & 0 & 0 & 2\\ 0 & 2 & -1 & 0\\ 1 & -3 & 0 & 1 \end{bmatrix}$

49)$\begin{bmatrix} 1 & -2 & 3 & 0\\ 0 & 1 & 0 & 2\\ 1 & 4 & -2 & 3\\ -5 & 0 & 1 & 1 \end{bmatrix}$

Responda: $\dfrac{1}{39}\begin{bmatrix} 3 & 2 & 1 & -7\\ 18 & -53 & 32 & 10\\ 24 & -36 & 21 & 9\\ -9 & 46 & -16 & -5 \end{bmatrix}$

50)$\begin{bmatrix} 1 & 2 & 0 & 2 & 3\\ 0 & 2 & 1 & 0 & 0\\ 0 & 0 & 3 & 0 & 1\\ 0 & 2 & 0 & 0 & 1\\ 0 & 0 & 1 & 2 & 0 \end{bmatrix}$

51)$\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 1 & 1 & 1 & 1 & 1 & 1 \end{bmatrix}$

Responda: $\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ -1 & -1 & -1 & -1 & -1 & 1 \end{bmatrix}$

Aplicativos do mundo real

Para os exercícios 52-61, escreva um sistema de equações que represente a situação. Em seguida, resolva o sistema usando o inverso de uma matriz.

52)$2,400$ ingressos foram vendidos para um jogo de basquete. Se os preços dos andares 1 e 2 fossem diferentes e a quantia total de dinheiro arrecadada fosse$\$64,000$, qual era o preço de cada ingresso?

53) No exercício anterior, se você soubesse que havia$400$ mais ingressos vendidos para o andar 2 do que para o andar 1, quanto era o preço de cada ingresso?

Responda: Soluções infinitas.

54) Uma campanha de alimentos coletou dois tipos diferentes de produtos enlatados, feijão verde e feijão vermelho. O número total de latas coletadas foi$350$ e o peso total de todos os alimentos doados foi de$348$ libras,$12$ onças. Se as latas de feijão verde pesarem$2$ onças a menos do que as latas de feijão, quantas de cada lata foram doadas?

55) Os alunos foram convidados a trazer suas frutas favoritas para a aula. $95\%$das frutas consistiam em banana, maçã e laranja. Se as laranjas eram duas vezes mais populares que as bananas e as maçãs eram$5\%$ menos populares do que as bananas, quais são as porcentagens de cada fruta individual?

Responda: $50\%$laranjas,$25\%$ bananas,$20\%$ maçãs

56) Uma irmandade realizou uma venda de bolos para arrecadar dinheiro e vendeu brownies e biscoitos de chocolate. Eles calcularam o preço dos brownies$\$1$ e dos biscoitos de chocolate em$\$0.75$. Eles criaram$\$700$ e venderam$850$ itens. Quantos brownies e quantos biscoitos foram vendidos?

57) Uma loja de roupas precisa solicitar um novo estoque. Tem três tipos diferentes de chapéus à venda: chapéus de palha, gorros e chapéus de cowboy. O chapéu de palha tem um preço$\$13.99$, o gorro em$\$7.99$, e o chapéu de cowboy em$\$14.49$. Se$100$ os chapéus foram vendidos no último trimestre,$\$1,119$ foram adquiridos pelas vendas e a quantidade de gorros vendidos foi$10$ maior do que chapéus de cowboy, quantos de cada um a loja de roupas deve pedir para substituir os já vendidos?

Responda: $10$chapéus de palha,$50$ gorros, chapéus de$40$ cowboy

58) Anna, Ashley e Andrea pesam uma$370$ libra combinada. Se Andrea pesa$20$ libras a mais do que Ashley e Anna pesa$1.5$ vezes mais que Ashley, quanto pesa cada garota?

59) Três colegas de quarto dividiram um pacote de$12$ sorvetes, mas ninguém se lembra de quem comeu quantas. Se Tom comeu duas vezes mais barras de sorvete do que Joe e Albert comeu três a menos do que Tom, quantas barras de sorvete cada colega de quarto comeu?

Responda: Tom comeu$6$, Joe comeu$3$ e Albert comeu$3$.

60) Um fazendeiro construiu um galinheiro com arame, madeira e madeira compensada. O custo do fio de galinha$\$2$ por metro quadrado, a madeira$\$10$ por pé quadrado e o compensado$\$5$ por pé quadrado. O fazendeiro gastou um total de$\$51$, e a quantidade total de materiais usados foi de$14$ pés ². Ele usou mais ^2$3$ pés de galinha do que madeira compensada. Quanto de cada material foi usado pelo agricultor?

61) Jay tem limoeiros, laranjeiras e romãs em seu quintal. Uma laranja pesa$8$ onças, uma$5$ onça de limão e uma$11$ onça de romã. Jay colheu$142$ pedaços de frutas pesando um total de$70$ libras,$10$ onças. Ele colheu$15.5$ vezes mais laranjas do que romãs. Quantas de cada fruta Jay colheu?

Responda: $124$laranjas,$10$ limões,$8$ romãs

9.8: Resolvendo sistemas com a regra de Cramer

Verbal

1) Explique por que sempre podemos avaliar o determinante de uma matriz quadrada.

Responda: Um determinante é a soma e os produtos das entradas na matriz, então você sempre pode avaliar esse produto, mesmo que acabe sendo$0$.

2) Examinando a Regra de Cramer, explique por que não existe uma solução única para o sistema quando o determinante de sua matriz é$0$. Para simplificar, use uma$2\times 2$ matriz.

3) Explique o que significa em termos de inverso que uma matriz tenha um$0$ determinante.

Responda: O inverso não existe.

4) O determinante da$2\times 2$ matriz$A$ é$3$. Se você trocar as linhas e multiplicar a primeira linha por$6$ e a segunda linha por$2$, explique como encontrar o determinante e forneça a resposta.

Algébrico

Para os exercícios 5-24, encontre o determinante.

5)$\begin{vmatrix} 1 & 2\\ 3 & 4 \end{vmatrix}$

Responda: $-2$

6)$\begin{vmatrix} -1 & 2\\ 3 & -4 \end{vmatrix}$

7)$\begin{vmatrix} 2 & -5\\ -1 & 6 \end{vmatrix}$

Responda: $7$

8)$\begin{vmatrix} -8 & 4\\ -1 & 5 \end{vmatrix}$

9)$\begin{vmatrix} 1 & 0\\ 3 & -4 \end{vmatrix}$

Responda: $-4$

10)$\begin{vmatrix} 10 & 20\\ 0 & -10 \end{vmatrix}$

11)$\begin{vmatrix} 10 & 0.2\\ 5 & 0.1 \end{vmatrix}$

Responda: $0$

12)$\begin{vmatrix} 6 & -3\\ 8 & 4 \end{vmatrix}$

13)$\begin{vmatrix} -2 & -3\\ 3.1 & 4,000 \end{vmatrix}$

Responda: $-7,990.7$

14)$\begin{vmatrix} -1.1 & 0.6\\ 7.2 & -0.5 \end{vmatrix}$

15)$\begin{vmatrix} -1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & -3 \end{vmatrix}$

Responda: $3$

16)$\begin{vmatrix} -1 & 4 & 0\\ 0 & 2 & 3\\ 0 & 0 & -3 \end{vmatrix}$

17)$\begin{vmatrix} 1 & 0 & 1\\ 0 & 1 & 0\\ 1 & 0 & 0 \end{vmatrix}$

Responda: $-1$

18)$\begin{vmatrix} 2 & -3 & 1\\ 3 & -4 & 1\\ -5 & 6 & 1 \end{vmatrix}$

19)$\begin{vmatrix} -2 & 1 & 4\\ -4 & 2 & -8\\ 2 & -8 & -3 \end{vmatrix}$

Responda: $224$

20)$\begin{vmatrix} 6 & -1 & 2\\ -4 & -3 & 5\\ 1 & 9 & -1 \end{vmatrix}$

21)$\begin{vmatrix} 5 & 1 & -1\\ 2 & 3 & 1\\ 3 & -6 & -3 \end{vmatrix}$

Responda: $15$

22)$\begin{vmatrix} 1.1 & 2 & -1\\ -4 & 0 & 0\\ 4.1 & -0.4 & 2.5 \end{vmatrix}$

23)$\begin{vmatrix} 2 & -1.6 & 3.1\\ 1.1 & 3 & -8\\ -9.3 & 0 & 2 \end{vmatrix}$

Responda: $-17.03$

24)$\begin{vmatrix} -\frac{1}{2} & \frac{1}{3} & \frac{1}{4}\\ \frac{1}{5} & -\frac{1}{6} & \frac{1}{7}\\ 0 & 0 & \frac{1}{8} \end{vmatrix}$

Para os exercícios 25-34, resolva o sistema de equações lineares usando a Regra de Cramer.

25)$\begin{align*} 2x-3y &= -1\\ 4x+5y &= 9 \end{align*}$

Responda: $(1,1)$

26)$\begin{align*} 5x-4y &= 2\\ -4x+7y &= 6 \end{align*}$

27)$\begin{align*} 6x-3y &= 2\\ -8x+9y &= -1 \end{align*}$

Responda: $\left (\dfrac{1}{2}, \dfrac{1}{3} \right )$

28)$\begin{align*} 2x+6y &= 12\\ 5x-2y &= 13 \end{align*}$

29)$\begin{align*} 4x+3y &= 23\\ 2x-y &= -1 \end{align*}$

Responda: $(2,5)$

30)$\begin{align*} 10x-6y &= 2\\ -5x+8y &= -1 \end{align*}$

31)$\begin{align*} 4x-3y &= -3\\ 2x+6y &= -4 \end{align*}$

Resposta: $\left (-1, -\dfrac{1}{3} \right )$

32)$\begin{align*} 4x-5y &= 7\\ -3x+9y &= 0 \end{align*}$

33)$\begin{align*} 4x+10y &= 180\\ -3x-5y &= -105 \end{align*}$

Resposta: $(15,12)$

34)$\begin{align*} 8x-2y &= -3\\ -4x+6y &= 4 \end{align*}$

Para os exercícios 35-44, resolva o sistema de equações lineares usando a Regra de Cramer.

(35)$\begin{align*} x+2y-4z &= -1\\ 7x+3y+5z &= 26\\ -2x-6y+7z &= -6 \end{align*}$

Resposta: $(1,3,2)$

36)$\begin{align*} -5x+2y-4z &= -47\\ 4x-3y-z &= -94\\ 3x-3y+2z &= 94 \end{align*}$

37)$\begin{align*} 4x+5y-z &= -7\\ -2x-9y+2z &= 8\\ 5y+7z &= 21 \end{align*}$

Resposta: $(-1,0,3)$

38)$\begin{align*} 4x-3y+4z &= 10\\ 5x-2z &= -2\\ 3x+2y-5z &= -9 \end{align*}$

39)$\begin{align*} 4x-2y+3z &= 6\\ -6x+y &= -2\\ 2x+7y+8z &= 24 \end{align*}$

Resposta: $\left (\dfrac{1}{2}, 1, 2 \right )$

40)$\begin{align*} 5x+2y-z &= 1\\ -7x-8y+3z &= 1.5\\ 6x-12y+z &= 7 \end{align*}$

41)$\begin{align*} 13x-17y+16z &= 73\\ -11x+15y+17z &= 61\\ 46x+10y-30z &= -18 \end{align*}$

Resposta: $(2,1,4)$

(42)$\begin{align*} -4x-3y-8z &= -7\\ 2x-9y+5z &= 0.5\\ 5x-6y-5z &= -2 \end{align*}$

43)$\begin{align*} 4x-6y+8z &= 10\\ -2x+3y-4z &= -5\\ x+y+z &= 1 \end{align*}$

Resposta: Soluções infinitas

44)$\begin{align*} 4x-6y+8z &= 10\\ -2x+3y-4z &= -5\\ 12x+18y-24z &= -30 \end{align*}$

Tecnologia

Para os exercícios 45-48, use a função determinante em um utilitário gráfico.

45)$\begin{vmatrix} 1 & 0 & 8 & 9\\ 0 & 2 & 1 & 0\\ 1 & 0 & 3 & 0\\ 0 & 2 & 4 & 3 \end{vmatrix}$

Resposta: $24$

(46)$\begin{vmatrix} 1 & 0 & 2 & 1\\ 0 & -9 & 1 & 3\\ 3 & 0 & -2 & -1\\ 0 & 1 & 1 & -2 \end{vmatrix}$

47)$\begin{vmatrix} \frac{1}{2} & 1 & 7 & 4\\ 0 & \frac{1}{2} & 100 & 5\\ 0 & 0 & 2 & 2,000\\ 0 & 0 & 0 & 2 \end{vmatrix}$

Resposta: $1$

48)$\begin{vmatrix} 1 & 0 & 0 & 0\\ 2 & 3 & 0 & 0\\ 4 & 5 & 6 & 0\\ 7 & 8 & 9 & 0 \end{vmatrix}$

Aplicativos do mundo real

Para os exercícios 49-52, crie um sistema de equações lineares para descrever o comportamento. Em seguida, calcule o determinante. Haverá uma solução única? Em caso afirmativo, encontre a solução exclusiva.

49) Dois números somam$56$. Um número é$20$ menor que o outro.

Resposta: Sim;$18$,$38$

50) Dois números somam$104$. Se você adicionar duas vezes o primeiro número mais duas vezes o segundo número, seu total será$208$

51) Três números somam$106$. O primeiro número é$3$ menor que o segundo número. O terceiro número é$4$ maior que o primeiro número.

Resposta: Sim;$33$,$36$,$37$

52) Três números se somam$216$. A soma dos dois primeiros números é$112$. O terceiro número é 8 a menos do que os dois primeiros números combinados.

Para os exercícios 53-65, crie um sistema de equações lineares para descrever o comportamento. Em seguida, resolva o sistema para todas as soluções usando a Regra de Cramer.

53) Você$\$10,000$ investe em duas contas, que recebem$8\%$ juros e$5\%$ juros. No final de um ano, você tinha$\$10,710$ em suas contas combinadas. Quanto foi investido em cada conta?

Resposta: $\$7,000$na primeira conta,$\$3,000$ na segunda conta.

54) Você$\$80,000$ investe em duas contas,$\$22,000$ em uma conta e$\$58,000$ na outra conta. No final de um ano, assumindo juros simples, você ganhou$\$2,470$ juros. A segunda conta recebe meio por cento menos que o dobro dos juros da primeira conta. Quais são as taxas de juros de suas contas?

55) Um cinema precisa saber quantos ingressos para adultos e crianças foram vendidos do$1,200$ total de ingressos. Se os ingressos para crianças são$\$5.95$, ingressos para adultos e o valor total da receita foi$\$12,756$, quantos ingressos para crianças e ingressos para adultos foram vendidos?$\$11.15$

Resposta: $120$crianças,$1,080$ adultos

56) Uma sala de concertos vende ingressos individuais para$\$40$ cada um e ingressos para casais para$\$65$. Se a receita total foi$\$18,090$ e os$321$ ingressos foram vendidos, quantos ingressos individuais e quantos ingressos para casais foram vendidos?

57) Você decide pintar sua cozinha de verde. Você cria a cor da tinta misturando tintas amarelas e azuis. Você não consegue se lembrar de quantos galões de cada cor entraram em sua mistura, mas você sabe que havia$10$ um total de garotas. Além disso, você guardou seu recibo e sabe o valor total gasto foi$\$29.50$. Se cada galão de amarelo custa$\$2.59$ e cada galão de azul custa$\$3.19$, quantos galões de cada cor entram em sua mistura de verde?

Resposta: $4$garota amarela,$6$ azul azul

58) Você vendeu dois tipos de lenços em um mercado de agricultores e gostaria de saber qual deles era mais popular. O número total de lenços vendidos foi$56$, o custo do lenço amarelo e o custo$\$10$ do lenço roxo$\$11$. Se você tivesse uma receita total de$\$583$, quantos lenços amarelos e quantos lenços roxos foram vendidos?

59) Seu jardim produziu dois tipos de tomate, um verde e um vermelho. O vermelho pesa$10$ onça e o verde pesa$4$ onças. Você tem$30$ tomates e um peso total de$13$ lb,$14$ oz. Quantos de cada tipo de tomate você tem?

Resposta: $13$tomates verdes, tomates$17$ vermelhos

60) Em um mercado, os três vegetais mais populares compõem as vendas$53\%$ de vegetais. O milho tem vendas$4\%$ mais altas do que o brócolis, que tem$5\%$ mais vendas do que a cebola. Qual a porcentagem de participação de mercado de cada vegetal?

61) No mesmo mercado, as três frutas mais populares compõem o total$37\%$ de frutas vendidas. Os morangos vendem duas vezes mais que as laranjas, e os kiwis vendem mais um ponto percentual do que as laranjas. Para cada fruta, encontre a porcentagem do total de frutas vendidas.

Resposta: Morangos$18\%$, laranjas$9\%$, kiwi$10\%$

62) Três bandas se apresentaram em uma sala de concertos. A primeira banda cobrada$\$15$ por ingresso, a segunda banda cobrada$\$45$ por ingresso e a última banda cobrada$\$22$ por ingresso. Foram vendidos$510$ ingressos, para um total de$\$12,700$. Se a primeira banda tivesse$40$ mais público do que a segunda banda, quantos ingressos foram vendidos para cada banda?

63) Um cinema vendeu ingressos para três filmes. Os ingressos para o primeiro filme foram$\$5$, os ingressos para o segundo filme foram$\$11$, e o terceiro filme foi$\$12$. $100$ingressos foram vendidos para o primeiro filme. O número total de ingressos vendidos foi$642$, para uma receita total de$\$6,774$. Quantos ingressos para cada filme foram vendidos?

Resposta: $100$para o filme 1,$230$ para o filme 2,$312$ para o filme 3

64) Homens envelheceram$20–29$ e$40–49$ eram constituídos pela população$78\%$ de uma prisão no ano passado.$30–39$ Este ano, as mesmas faixas etárias foram$82.08\%$ compostas pela população. A$20–29$ faixa etária aumentou$20%$, a$30–39$ faixa etária aumentou$2\%$ e a$40–49$ faixa etária diminuiu para$\dfrac{3}{4}$ a população anterior. Originalmente, a$30–39$ faixa etária tinha$2\%$ mais prisioneiros do que a$20–29$ faixa etária. Determine a porcentagem da população carcerária para cada faixa etária no ano passado.

65) Em uma prisão feminina no final da estrada, o número total de presidiárias com idade$20–49$ totalizou$5,525$. Este ano, a$20–29$ faixa etária aumentou$10\%$, a$30–39$ faixa etária$20\%$ diminuiu e a$40–49$ faixa etária dobrou. Agora existem$6,040$ prisioneiros. Originalmente, havia$500$ mais na$30–39$ faixa etária do que na$20–29$ faixa etária. Determine a população carcerária para cada faixa etária no ano passado.

Resposta: $20–29: 2,100$,$30–39: 2,600$,$40–49: 825$

Para os exercícios 66-68, use este cenário: uma empresa preocupada com a saúde decide fazer uma mistura de trilhas com amêndoas, cranberries secas e cajus cobertos com chocolate. As informações nutricionais desses itens são mostradas na Tabela abaixo.

	Gordura (g)	Proteína (g)	Carboidratos (g)
Amêndoas (10)	6	2	3
Cranberries (10)	0,02	0	8
Castanha de caju (10)	7	3.5	5.5

66) Para a mistura especial de trilhas “low carb”, há$1,000$ pedaços de mistura. O número total de carboidratos é$425$ g e a quantidade total de gordura é$570.2$ g. Se houver$200$ mais pedaços de castanha de caju do que cranberries, quantos de cada item estão na mistura de trilha?

67) Para a mistura “caminhada”, há$1,000$ pedaços na mistura, contendo$390.8$ g de gordura e$165$ g de proteína. Se houver a mesma quantidade de amêndoas que a castanha de caju, quantos de cada item estão no mix da trilha?

Resposta: $300$amêndoas,$400$ cranberries,$300$ castanha de caju

68) Para a mistura “energy-booster”, há$1,000$ pedaços na mistura, contendo$145$ g de proteína e$625$ g de carboidratos. Se o número de amêndoas e castanhas de caju somadas for equivalente à quantidade de cranberries, quantos de cada item estão no mix de trilhas?

Contribuidores e atribuições

Template:OpenStaxPreCalc