9.5: Matrizes e operações matriciais
- Page ID
- 189136
- Encontre a soma e a diferença de duas matrizes.
- Encontre múltiplos escalares de uma matriz.
- Encontre o produto de duas matrizes.
Dois times de futebol de clubes, os Wildcats e os Mud Cats, esperam obter novos equipamentos para a próxima temporada. A tabela\(\PageIndex{1}\) mostra as necessidades de ambas as equipes.
| Gatos selvagens | Gatos de lama | |
|---|---|---|
| Objetivos | 6 | 10 |
| Bolas | 30 | 24 |
| Camisolas | 14 | 20 |
Um gol custa\($300\); uma bola custa\($10\); e uma camisa custa\($30\). Como podemos encontrar o custo total do equipamento necessário para cada equipe? Nesta seção, descobrimos um método no qual os dados na tabela de equipamentos de futebol podem ser exibidos e usados para calcular outras informações. Em seguida, poderemos calcular o custo do equipamento.

Encontrando a soma e a diferença de duas matrizes
Para resolver um problema como o descrito para os times de futebol, podemos usar uma matriz, que é uma matriz retangular de números. Uma linha em uma matriz é um conjunto de números alinhados horizontalmente. Uma coluna em uma matriz é um conjunto de números alinhados verticalmente. Cada número é uma entrada, às vezes chamada de elemento, da matriz. As matrizes (plural) estão entre [] ou () e geralmente são nomeadas com letras maiúsculas. Por exemplo, três matrizes chamadas\(A\)\(B\), e\(C\) são mostradas abaixo.
\[ \begin{align*} A&=\begin{bmatrix} 1& 2 \\ 3 & 4 \\ \end{bmatrix} \\[4pt] B &=\begin{bmatrix} 1 & 2 & 7 \\ 0 & -5 & 6 \\ 7 & 8 & 2 \end{bmatrix} \\[4pt] C &=\begin{bmatrix} -1 & 3 \\ 0 & 2 \\ 3 & 1 \end{bmatrix} \end{align*}\]
Uma matriz geralmente é referida por seu tamanho ou dimensões:\(m×n\) indicando\(m\) linhas e\(n\) colunas. As entradas da matriz são definidas primeiro por linha e depois por coluna. Por exemplo, para localizar a entrada na matriz\(A\) identificada como\(a_{ij}\), procuramos a entrada em linha\(i\), coluna\(j\). Na matriz\(A\), mostrada abaixo, a entrada em linha\(2\), coluna\(3\) é\(a_{23}\).
\[A=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33} \end{bmatrix} \nonumber\]
- Uma matriz quadrada é uma matriz com dimensões\(n × n\), o que significa que ela tem o mesmo número de linhas que as colunas. A\(3×3\) matriz acima é um exemplo de matriz quadrada.
- Uma matriz de linhas é uma matriz que consiste em uma linha com dimensões\(1 × n\). \[\begin{bmatrix} a_{11} & a_{12} & a_{13} \end{bmatrix} \nonumber\]
- Uma matriz de coluna é uma matriz que consiste em uma coluna com dimensões\(m × 1\). \[\begin{bmatrix} a_{11} \\ a_{21} \\a_{31} \end{bmatrix} \nonumber\]
Uma matriz pode ser usada para representar um sistema de equações. Nesses casos, os números representam os coeficientes das variáveis no sistema. As matrizes geralmente facilitam a resolução de sistemas de equações porque elas não estão sobrecarregadas com variáveis. Investigaremos essa ideia mais detalhadamente na próxima seção, mas primeiro examinaremos as operações matriciais básicas.
Uma matriz é uma matriz retangular de números que geralmente é nomeada por uma letra maiúscula:\(A\)\(B\),\(C\), e assim por diante. Cada entrada em uma matriz é chamada de\(a_{ij}\), de forma que\(i\) represente a linha e\(j\) represente a coluna. As matrizes geralmente são referidas por suas dimensões:\(m × n\) indicando\(m\) linhas e\(n\) colunas.
Matriz dada\(A\):
- Quais são as dimensões da matriz\(A\)?
- Quais são as entradas em\(a_{31}\) e\(a_{22}\)?
\[A=\begin{bmatrix} 2 & 1 & 0\\2 & 4 & 7\\3 & 1 & −2 \end{bmatrix} \nonumber\]
Solução
- As dimensões são\(3 \times 3\) porque há três linhas e três colunas.
- A entrada\(a_{31}\) é o número na linha 3, coluna 1, que é\(3\). A entrada\(a_{22}\) é o número na linha 2, coluna 2, que é\(4\). Lembre-se de que a linha vem primeiro, depois a coluna.
Adicionando e subtraindo matrizes
Usamos matrizes para listar dados ou representar sistemas. Como as entradas são números, podemos realizar operações em matrizes. Nós adicionamos ou subtraímos matrizes adicionando ou subtraindo as entradas correspondentes. Para fazer isso, as entradas devem corresponder. Portanto, a adição e a subtração de matrizes só são possíveis quando as matrizes têm as mesmas dimensões. Podemos adicionar ou subtrair uma\(3 \times 3\) matriz e outra\(3 \times 3\) matriz, mas não podemos adicionar ou subtrair uma\(2 \times 3\)\(3 \times 3\) matriz e uma matriz porque algumas entradas em uma matriz não terão uma entrada correspondente na outra matriz.
Dadas matrizes\(A\) e\(B\) de dimensões semelhantes, a adição e subtração de\(A\) e\(B\) produzirá uma matriz\(C\) ou matriz\(D\) da mesma dimensão.
\[A+B=C\]
de tal forma que\(a_{ij}+b_{ij}=c_{ij}\)
\[A−B=D\]
de tal forma que\(a_{ij}−b_{ij}=d_{ij}\)
A adição de matriz é comutativa.
\[A+B=B+A\]
Também é associativo.
\[(A+B)+C=A+(B+C)\]
Encontre a soma de\(A\) e\(B\), dada
\[A=\begin{bmatrix}a & b\\c & d \end{bmatrix} \nonumber\]
e
\[B=\begin{bmatrix}e & f\\g & h\end{bmatrix} \nonumber\]
Solução
Adicione as entradas correspondentes.
\[\begin{align} A+B &=\begin{bmatrix}a & b\\c & d\end{bmatrix}+\begin{bmatrix}e & f\\g & h\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}a+e & b+f\\c+g & d+h \end{bmatrix} \nonumber \end{align} \nonumber\]
Encontre a soma de\(A\)\(B\) e.
\[A=\begin{bmatrix}4 &1\\3 & 2 \end{bmatrix} \nonumber\]
e
\[B=\begin{bmatrix}5 & 9\\0 & 7\end{bmatrix} \nonumber\]
Solução
Adicione as entradas correspondentes. Adicione a entrada na linha 1, coluna 1,\(a_{11}\), da matriz\(A\) à entrada na linha 1, coluna 1,\(b_{11}\), de\(B\). Continue com o padrão até que todas as entradas tenham sido adicionadas.
\[\begin{align} A+B &=\begin{bmatrix}4&1\\3 &2\end{bmatrix}+\begin{bmatrix}5&9\\0&7\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}4+5&1+9\\3+0&2+7\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}9&10\\3&9\end{bmatrix} \nonumber \end{align} \nonumber\]
Descubra a diferença de\(A\)\(B\) e.
\(A=\begin{bmatrix}−2&3\\0&1\end{bmatrix}\)e\(B=\begin{bmatrix}8&1\\5&4\end{bmatrix}\)
Solução
Subtraímos as entradas correspondentes de cada matriz.
\[\begin{align} A−B &=\begin{bmatrix}−2&3\\0&1\end{bmatrix}−\begin{bmatrix}8&1\\5&4\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}−2−8&3−1\\0−5&1−4\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}−10&2\\−5&−3\end{bmatrix} \nonumber \end{align} \nonumber\]
Dado\(A\) e\(B\):
- Encontre a soma.
- Descubra a diferença.
\[A=\begin{bmatrix}2&−10&−2\\14&12&10\\4&−2&2\end{bmatrix} \nonumber\]
e
\[B=\begin{bmatrix}6&10&−2\\0&−12&−4\\−5&2&−2\end{bmatrix} \nonumber\]
Solução
- Adicione as entradas correspondentes.
\[\begin{align} A+B & =\begin{bmatrix} 2& −10& −2\\14 & 12 & 10\\4 & −2 & 2\end{bmatrix}+\begin{bmatrix}6 & 10 & −2\\0 & −12 & −4\\−5 & 2 & −2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}2+6 & −10+10 & −2−2\\14+0 & 12−12 & 10−4\\4−5 & −2+2 & 2−2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix} 8 & 0 & −4\\14 & 0 & 6\\−1 & 0 & 0\end{bmatrix} \nonumber \end{align} \nonumber\]
- Subtraia as entradas correspondentes.
\[\begin{align} A−B &=\begin{bmatrix}2&−10&−2\\14&12&10\\4&−2&2\end{bmatrix}−\begin{bmatrix}6&10&−2\\0&−12&−4\\−5&2&−2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}2−6 & −10−10 & −2+2\\14−0 & 12+12 & 10+4\\4+5 & −2−2 & 2+2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−4 & −20 & 0\\14 & 24 & 14\\9 & −4 & 4\end{bmatrix} \nonumber \end{align} \nonumber\]
Adicione matriz\(A\) e matriz\(B\).
\[A=\begin{bmatrix}2&6\\1&0\\1&−3\end{bmatrix} \nonumber\]
e
\[B=\begin{bmatrix}3&−2\\1&5\\−4&3\end{bmatrix} \nonumber\]
- Responda
-
\[\begin{align} A+B&=\begin{bmatrix}2&6\\ 1 &0\\1&−3\end{bmatrix}+\begin{bmatrix} 3&-2 \\1&5 \\-4&3\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}2+3&6+(−2)\\1+1&0+5\\1+(-4)&−3+3\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}5&4\\2&5\\-3&0\end{bmatrix} \nonumber \end{align} \nonumber\]
Encontrando múltiplos escalares de uma matriz
Além de somar e subtrair matrizes inteiras, há muitas situações em que precisamos multiplicar uma matriz por uma constante chamada escalar. Lembre-se de que um escalar é uma quantidade numérica real que tem magnitude, mas não direção. Por exemplo, tempo, temperatura e distância são quantidades escalares. O processo de multiplicação escalar envolve a multiplicação de cada entrada em uma matriz por um escalar. Um múltiplo escalar é qualquer entrada de uma matriz que resulta da multiplicação escalar.
Considere um cenário do mundo real em que uma universidade precisa aumentar seu inventário de computadores, mesas de computador e cadeiras em dois dos laboratórios do campus devido ao aumento de matrículas. Eles estimam que\(15%\) mais equipamentos são necessários em ambos os laboratórios. O inventário atual da escola é exibido na Tabela\(\PageIndex{2}\).
| Laboratório A | Laboratório B | |
|---|---|---|
| Computadores | 15 | 27 |
| Mesas de computador | 16 | 34 |
| Cadeiras | 16 | 34 |
Convertendo os dados em uma matriz, temos
\[C_{2013}=\begin{bmatrix}15 & 27\\16&34\\16&34\end{bmatrix} \nonumber\]
Para calcular a quantidade de equipamento de computador necessário, multiplicamos todas as entradas na matriz\(C\) por\(0.15\).
\[(0.15)C_{2013}=\begin{bmatrix}(0.15)15&(0.15)27\\(0.15)16&(0.15)34\\(0.15)16 &(0.15)34\end{bmatrix}=\begin{bmatrix}2.25 &4.05\\2.4&5.1\\2.4&5.1\end{bmatrix} \nonumber\]
Devemos arredondar para o próximo número inteiro, então a quantidade de novos equipamentos necessários é
\[\begin{bmatrix}3&5\\3&6\\3&6\end{bmatrix} \nonumber\]
Adicionando as duas matrizes, conforme mostrado abaixo, vemos os novos valores de estoque.
\[\begin{bmatrix}15&27\\16&34\\16&34\end{bmatrix}+\begin{bmatrix}3&5\\3&6\\3&6\end{bmatrix}=\begin{bmatrix}18&32\\19&40\\19&40\end{bmatrix} \nonumber\]
Isso significa
\[C_{2014}=\begin{bmatrix}18&32\\19&40\\19&40\end{bmatrix} \nonumber\]
Assim, o Laboratório A terá\(18\) computadores, mesas de\(19\) computador e\(19\) cadeiras; o Laboratório B terá\(32\) computadores, mesas de\(40\) computador e\(40\) cadeiras.
A multiplicação escalar envolve encontrar o produto de uma constante por cada entrada na matriz. Dado
\[A=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix} \nonumber\]
o múltiplo escalar\(cA\) é
\[cA=c\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix} \nonumber\]
\[=\begin{bmatrix}ca_{11}&ca_{12}\\ca_{21}&ca_{22}\end{bmatrix} \nonumber\]
A multiplicação escalar é distributiva. Para as matrizes\(A\),\(B\), e\(C\) com escalares\(a\) e\(b\),
\[a(A+B)=aA+aB\]
\[(a+b)A=aA+bA\]
Multiplique a matriz\(A\) pelo escalar\(3\).
\[A=\begin{bmatrix}8&1\\5&4\end{bmatrix} \nonumber\]
Solução
Multiplique cada entrada\(A\) pelo escalar\(3\).
\[ \begin{align} 3A&=3\begin{bmatrix}8&1\\5&4\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}3⋅8&3⋅1\\3⋅5&3⋅4\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}24&3\\15&12\end{bmatrix} \nonumber \end{align} \nonumber\]
Dada matriz\(B\), descubra\(−2B\) onde
\[B=\begin{bmatrix}4&1\\3&2\end{bmatrix} \nonumber\]
- Responda
-
\[−2B=\begin{bmatrix}−8&−2\\−6&−4\end{bmatrix} \nonumber\]
Encontre a soma\(3A+2B\).
\[A=\begin{bmatrix}1&−2&0\\0&−1&2\\4&3&−6\end{bmatrix} \nonumber\]
e
\[B=\begin{bmatrix}−1&2&1\\0&−3&2\\0&1&−4\end{bmatrix} \nonumber\]
Solução
Primeiro, encontre\(3A\), então\(2B\).
\[ \begin{align} 3A&=\begin{bmatrix}3⋅1&3(−2)&3⋅0\\3⋅0&3(−1)&3⋅2\\3⋅4&3⋅3&3(−6)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}3&−6&0\\0&−3&6\\12&9&−18\end{bmatrix}\nonumber \end{align} \nonumber\]
\[ \begin{align} 2B&=\begin{bmatrix}2(−1)&2⋅2&2⋅1\\2⋅0&2(−3)&2⋅2\\2⋅0&2⋅1&2(−4)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−2&4&2\\0&−6&4\\0&2&−8\end{bmatrix}\nonumber \end{align} \nonumber\]
Agora, adicione\(3A+2B\).
\[ \begin{align} 3A+2B&=\begin{bmatrix}3&−6&0\\0&−3&6\\12&9&−18\end{bmatrix}+\begin{bmatrix}−2&4&2\\0&−6&4\\0&2&−8\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}3−2&−6+4&0+2\\0+0&−3−6&6+4\\12+0&9+2&−18−8\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}1& −2&2\\0&−9&10\\12&11&−26\end{bmatrix} \nonumber \end{align} \nonumber\]
Encontrando o produto de duas matrizes
Além de multiplicar uma matriz por um escalar, podemos multiplicar duas matrizes. Encontrar o produto de duas matrizes só é possível quando as dimensões internas são as mesmas, o que significa que o número de colunas da primeira matriz é igual ao número de linhas da segunda matriz. Se\(A\) for uma\(m × r\) matriz e\(B\) for uma\(r × n\) matriz, então a matriz do produto\(AB\) é uma\(m × n\) matriz. Por exemplo, o produto\(AB\) é possível porque o número de colunas em\(A\) é o mesmo que o número de linhas em\(B\). Se as dimensões internas não coincidirem, o produto não está definido.
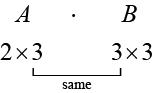
Multiplicamos as entradas de\(A\) por entradas de\(B\) acordo com um padrão específico, conforme descrito abaixo. O processo de multiplicação de matrizes se torna mais claro quando se trabalha um problema com números reais.
Para obter as entradas na linha\(i\) de\(AB\), multiplicamos as entradas em linha\(i\) de\(A\) por coluna\(j\)\(B\) e adicionamos. Por exemplo, dadas as matrizes\(A\) e\(B\), onde as dimensões de\(A\) são\(2 \times 3\) e as dimensões de\(B\) são\(3 \times 3\), o produto de\(AB\) será uma\(2 \times 3\) matriz.
\[A=\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\end{bmatrix} \nonumber \]
e
\[B=\begin{bmatrix}b_{11}&b_{12}&b_{13}\\b_{21}&b_{22}&b_{23}\\b_{31}&b_{32}&b_{33}\end{bmatrix} \nonumber\]
Multiplique e adicione da seguinte forma para obter a primeira entrada da matriz do produto\(AB\).
- Para obter a entrada na linha 1, coluna 1 de\(AB\), multiplique a primeira linha\(A\) pela primeira coluna em\(B\) e adicione.
\[\begin{bmatrix}a_{11}&a_{12}&a_{13}\end{bmatrix} ⋅\begin{bmatrix}b_{11}\\b_{21}\\b_{31}\end{bmatrix}=a_{11}⋅b_{11}+a_{12}⋅b_{21}+a_{13}⋅b_{31} \nonumber \]
- Para obter a entrada na linha 1, coluna 2 de\(AB\), multiplique a primeira linha de\(A\) pela segunda coluna em\(B\) e adicione.
\[\begin{bmatrix}a_{11}&a_{12}&a_{13}\end{bmatrix} ⋅\begin{bmatrix}b_{12}\\b_{22}\\b_{32}\end{bmatrix}=a_{11}⋅b_{12}+a_{12}⋅b_{22}+a_{13}⋅b_{32} \nonumber \]
- Para obter a entrada na linha 1, coluna 3 de\(AB\), multiplique a primeira linha de\(A\) pela terceira coluna em\(B\) e adicione.
\[\begin{bmatrix}a_{11}&a_{12}&a_{13}\end{bmatrix} ⋅\begin{bmatrix}b_{13}\\b_{23}\\b_{33}\end{bmatrix}=a_{11}⋅b_{13}+a_{12}⋅b_{23}+a_{13}⋅b_{33} \nonumber \]
Procedemos da mesma maneira para obter a segunda linha de\(AB\). Em outras palavras, linha 2 de\(A\) vezes coluna 1 de\(B\); linha 2 de\(A\) vezes coluna 2 de\(B\); linha 2 de\(A\) vezes coluna 3 de\(B\). Quando concluída, a matriz do produto será
\[AB=\begin{bmatrix}a_{11}⋅b_{11}+a_{12}⋅b_{21}+a_{13}⋅b_{31} &a_{11}⋅b_{12}+a_{12}⋅b_{22}+a_{13}⋅b_{32}&a_{11}⋅b_{13}+a_{12}⋅b_{23}+a_{13}⋅b_{33} \\a_{21}⋅b_{11}+a_{22}⋅b_{21}+a_{23}⋅b_{31}&a_{21}⋅b_{12}+a_{22}⋅b_{22}+a_{23}⋅b_{32}&a_{21}⋅b_{13}+a_{22}⋅b_{23}+a_{23}⋅b_{33}\end{bmatrix} \nonumber\]
Para a matriz\(A, B\), e\(C\) as propriedades a seguir são válidas.
- A multiplicação de matrizes é associativa:\[(AB)C=A(BC).\]
- A multiplicação de matrizes é distributiva:\[C(A+B)=CA+CB\]\[(A+B)C=AC+BC.\]
Observe que a multiplicação de matrizes não é comutativa.
Multiplique matriz\(A\) e matriz\(B\).
\[A=\begin{bmatrix}1&2\\3&4\end{bmatrix} \nonumber\]
e
\[B=\begin{bmatrix}5&6\\7&8\end{bmatrix} \nonumber\]
Solução
Primeiro, verificamos as dimensões das matrizes. \(A\)A matriz tem dimensões\(2 × 2\) e a matriz\(B\) tem dimensões\(2 × 2\). As dimensões internas são as mesmas para que possamos realizar a multiplicação. O produto terá as dimensões\(2 × 2\).
Realizamos as operações descritas anteriormente.
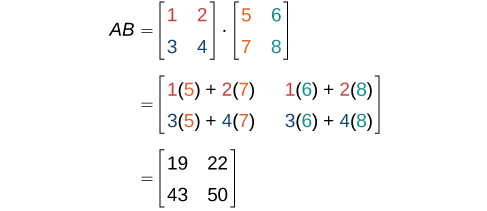
Dado\(A\) e\(B\):
- Encontre\(AB\).
- Encontre\(BA\).
\[A=\begin{bmatrix}−1&2&3\\ 4&0&5\end{bmatrix} \nonumber\]
e
\[B=\begin{bmatrix}5&−1\\-4&0\\2&3\end{bmatrix} \nonumber\]
Solução
- Como as dimensões de\(A\) são\(2 \times 3\) e as dimensões de\(B\) são\(3 \times 2\), essas matrizes podem ser multiplicadas juntas porque o número de colunas em\(A\) corresponde ao número de linhas em\(B\). O produto resultante será uma\(2 \times 2\) matriz, o número de linhas em\(A\) pelo número de colunas em\(B\).
\[ \begin{align}AB&=\begin{bmatrix}−1&2&3\\4&0&5\end{bmatrix} \begin{bmatrix}5&−1\\−4&0\\2&3\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−1(5)+2(−4)+3(2)&−1(−1)+2(0)+3(3)\\4(5)+0(−4)+5(2)&4(−1)+0(0)+5(3)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−7&10\\30&11\end{bmatrix} \nonumber \end{align} \nonumber\]
- As dimensões de\(B\) são\(3 \times 2\) e as dimensões de\(A\) são\(2 \times 3\). As dimensões internas coincidem, então o produto é definido e será uma\(3 \times 3\) matriz.
\[ \begin{align}BA&=\begin{bmatrix}5&−1\\−4&0\\2&3\end{bmatrix} \begin{bmatrix} −1&2&3\\4&0&5\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}5(−1)+−1(4)&5(2)+−1(0)&5(3)+−1(5)\\−4(−1)+0(4)&−4(2)+0(0)&−4(3)+0(5)\\2(−1)+3(4)& 2(2)+3(0)&2(3)+3(5)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−9&10&10\\4&−8&−12\\10&4&21\end{bmatrix} \nonumber \end{align} \nonumber\]
Análise
Observe que os produtos\(AB\) não\(BA\) são iguais.
\[AB=\begin{bmatrix}−7&10\\30&11\end{bmatrix}≠ \begin{bmatrix}−9&10&10\\4&−8&−12\\10&4&21\end{bmatrix}=BA \nonumber\]
Isso ilustra o fato de que a multiplicação de matrizes não é comutativa.
Sim, considere uma matriz\(A\) com dimensão\(3 × 4\) e uma matriz\(B\) com dimensão\(4 × 2\). Para o produto\(AB\), as dimensões internas são\(4\) e o produto está definido, mas para o produto\(BA\) as dimensões internas são\(2\) e\(3\), portanto, o produto é indefinido.
Vamos voltar ao problema apresentado na abertura desta seção. Temos uma mesa\(\PageIndex{3}\), representando as necessidades de equipamento de dois times de futebol.
| Gatos selvagens | Gatos de lama | |
|---|---|---|
| Objetivos | 6 | 10 |
| Bolas | 30 | 24 |
| Camisolas | 14 | 20 |
Também recebemos os preços do equipamento, conforme mostrado na Tabela\(\PageIndex{4}\).
| Objetivo | $300 |
| Bola | $10 |
| Jersey | $30 |
Vamos converter os dados em matrizes. Assim, a matriz de necessidades do equipamento é escrita como
\[E=\begin{bmatrix}6&10\\30&24\\14&20\end{bmatrix} \nonumber\]
A matriz de custos é escrita como
\[C=\begin{bmatrix}300&10&30\end{bmatrix} \nonumber\]
Realizamos a multiplicação de matrizes para obter os custos do equipamento.
\[ \begin{align} CE&=\begin{bmatrix}300&10&30\end{bmatrix}⋅\begin{bmatrix}6&10\\30&24\\14&20\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}300(6)+10(30)+30(14)&300(10)+10(24)+30(20)\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}2,520&3,840\end{bmatrix} \nonumber \end{align} \nonumber\]
O custo total do equipamento para os Wildcats é\($2,520\), e o custo total do equipamento para os Mud Cats é\($3,840\).
- Salve cada matriz como uma variável de matriz\([A], [B], [C],...\)
- Insira a operação na calculadora, chamando cada variável da matriz conforme necessário.
- Se a operação for definida, a calculadora apresentará a matriz da solução; se a operação for indefinida, ela exibirá uma mensagem de erro.
Encontre\(AB−C\) dado
\(A=\begin{bmatrix}−15&25&32\\41&−7&−28\\10&34&−2\end{bmatrix}\),\(B=\begin{bmatrix}45&21&−37\\−24&52&19\\6&−48&−31\end{bmatrix}\), e\(C=\begin{bmatrix}−100&−89&−98\\25&−56&74\\−67&42&−75\end{bmatrix}\)
Solução
Na página da matriz da calculadora, inserimos a matriz\(A\) acima como a variável da matriz\([ A ]\), a matriz\(B\) acima como a variável\([ B ]\) da matriz e a matriz\(C\) acima como a variável da matriz\([ C ]\).
Na tela inicial da calculadora, digitamos o problema e acessamos cada variável da matriz conforme necessário.
\[[A]×[B]−[C] \nonumber\]
A calculadora nos fornece a seguinte matriz.
\[\begin{bmatrix}−983&−462&136\\1,820&1,897&−856\\−311&2,032&413\end{bmatrix} \nonumber\]
Acesse esses recursos on-line para obter instruções e práticas adicionais com matrizes e operações matriciais.
Conceitos-chave
- Uma matriz é uma matriz retangular de números. As entradas são organizadas em linhas e colunas.
- As dimensões de uma matriz se referem ao número de linhas e ao número de colunas. Uma\(3×2\) matriz tem três linhas e duas colunas. Veja o exemplo\(\PageIndex{1}\).
- Somamos e subtraímos matrizes de dimensões iguais adicionando e subtraindo as entradas correspondentes de cada matriz. Veja exemplo\(\PageIndex{2}\), exemplo\(\PageIndex{3}\)\(\PageIndex{4}\), exemplo e exemplo\(\PageIndex{5}\).
- A multiplicação escalar envolve a multiplicação de cada entrada em uma matriz por uma constante. Veja o exemplo\(\PageIndex{6}\).
- A multiplicação escalar geralmente é necessária antes que a adição ou a subtração possam ocorrer. Veja o exemplo\(\PageIndex{7}\).
- A multiplicação de matrizes é possível quando as dimensões internas são as mesmas — o número de colunas na primeira matriz deve corresponder ao número de linhas na segunda.
- O produto de duas matrizes,\(A\) e\(B\), é obtido multiplicando cada entrada na linha 1 de\(A\) por cada entrada na coluna 1 de\(B\); em seguida, multiplique cada entrada da linha 1 de\(A\) por cada entrada nas colunas 2 de\(B\), e assim por diante. Veja o exemplo\(\PageIndex{8}\) e o exemplo\(\PageIndex{9}\).
- Muitos problemas do mundo real geralmente podem ser resolvidos usando matrizes. Veja o exemplo\(\PageIndex{10}\).
- Podemos usar uma calculadora para realizar operações matriciais depois de salvar cada matriz como uma variável de matriz. Veja o exemplo\(\PageIndex{11}\).


