9.3: Sistemas de equações e desigualdades não lineares - duas variáveis
- Page ID
- 189168
- Resolva um sistema de equações não lineares usando substituição.
- Resolva um sistema de equações não lineares usando eliminação.
- Representar graficamente uma desigualdade não linear.
- Faça um gráfico de um sistema de desigualdades não lineares.
O cometa Halley (Figura\(\PageIndex{1}\)) orbita o sol cerca de uma vez a cada\(75\) ano. Seu caminho pode ser considerado uma elipse muito alongada. Outros cometas seguem caminhos semelhantes no espaço. Esses caminhos orbitais podem ser estudados usando sistemas de equações. Esses sistemas, no entanto, são diferentes dos que consideramos na seção anterior porque as equações não são lineares.

Figura\(\PageIndex{1}\): Cometa Halley (crédito: “NASA Blueshift” /Flickr)
Nesta seção, consideraremos a interseção de uma parábola e uma linha, um círculo e uma linha e um círculo e uma elipse. Os métodos para resolver sistemas de equações não lineares são semelhantes aos de equações lineares.
Resolvendo um sistema de equações não lineares usando substituição
Um sistema de equações não lineares é um sistema de duas ou mais equações em duas ou mais variáveis contendo pelo menos uma equação que não seja linear. Lembre-se de que uma equação linear pode assumir a forma\(Ax+By+C=0\). Qualquer equação que não possa ser escrita dessa forma de forma não linear. O método de substituição que usamos para sistemas lineares é o mesmo método que usaremos para sistemas não lineares. Resolvemos uma equação para uma variável e, em seguida, substituímos o resultado na segunda equação para resolver outra variável, e assim por diante. Há, no entanto, uma variação nos resultados possíveis.
Interseção de uma parábola e uma linha
Existem três tipos possíveis de soluções para um sistema de equações não lineares envolvendo uma parábola e uma linha.
\(\PageIndex{2}\)A figura ilustra possíveis conjuntos de soluções para um sistema de equações envolvendo uma parábola e uma linha.
- Sem solução - A linha nunca cruzará a parábola.
- Uma solução - A linha é tangente à parábola e cruza a parábola em exatamente um ponto.
- Duas soluções - A linha cruza na parte interna da parábola e cruza a parábola em dois pontos.
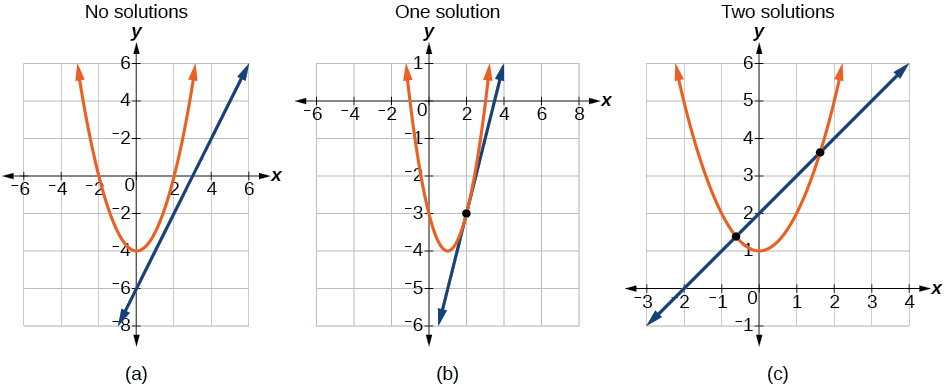
Figura\(\PageIndex{2}\)
- Resolva a equação linear para uma das variáveis.
- Substitua a expressão obtida na etapa um na equação da parábola.
- Resolva a variável restante.
- Verifique suas soluções nas duas equações.
Resolva o sistema de equações.
\[\begin{align*} x−y &= −1\nonumber \\ y &= x^2+1 \nonumber \end{align*}\]
Solução
Resolva a primeira equação\(x\) e, em seguida, substitua a expressão resultante na segunda equação.
\[\begin{align*} x−y &=−1\nonumber \\ x &= y−1 \;\; & \text{Solve for }x.\nonumber \\\nonumber \\ y &=x^2+1\nonumber \\ y & ={(y−1)}^2+1 \;\; & \text{Substitute expression for }x. \nonumber \end{align*}\]
Expanda a equação e defina-a como igual a zero.
\[ \begin{align*} y & ={(y−1)}^2+1\nonumber \\ &=(y^2−2y+1)+1\nonumber \\ &=y^2−2y+2\nonumber \\ 0 &= y^2−3y+2\nonumber \\ &= (y−2)(y−1) \nonumber \end{align*}\]
Resolvendo\(y\)\(y=2\) doações\(y=1\) e. Em seguida, substitua cada valor por\(y\) na primeira equação a ser resolvida\(x\). Sempre substitua o valor na equação linear para verificar se há soluções estranhas.
\[\begin{align*} x−y &=−1\nonumber \\ x−(2) &= −1\nonumber \\ x &= 1\nonumber \\ x−(1) &=−1\nonumber \\ x &= 0 \nonumber \end{align*}\]
As soluções são\((1,2)\) e\((0,1)\), que podem ser verificadas substituindo esses\((x,y)\) valores nas duas equações originais (Figura\(\PageIndex{3}\)).
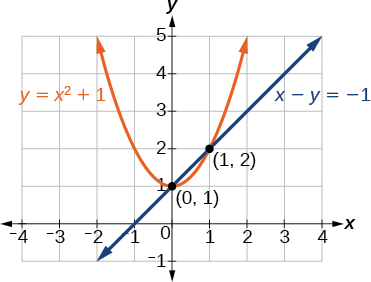
Figura\(\PageIndex{3}\)
Sim, mas como\(x\) está ao quadrado na segunda equação, isso pode nos dar soluções estranhas para\(x\).
Para\(y=1\)
\[\begin{align*} y &= x^2+1\nonumber \\ y &= x^2+1\nonumber \\ x^2 &= 0\nonumber \\ x &= \pm \sqrt{0}=0 \nonumber \end{align*}\]
Isso nos dá o mesmo valor da solução.
Para\(y=2\)
\[\begin{align*} y &= x^2+1\nonumber \\ 2 &= x^2+1\nonumber \\ x^2 &= 1\nonumber \\ x &= \pm \sqrt{1}=\pm 1 \nonumber \end{align*}\]
Observe que\(−1\) é uma solução estranha.
Resolva o sistema de equações fornecido por substituição.
\[\begin{align*} 3x−y &= −2\nonumber \\ 2x^2−y &= 0 \nonumber \end{align*}\]
- Resposta
-
\(\left(−\dfrac{1}{2},\dfrac{1}{2}\right)\)e\((2,8)\)
Interseção de um círculo e uma linha
Assim como com uma parábola e uma linha, há três resultados possíveis ao resolver um sistema de equações representando um círculo e uma linha.
\(\PageIndex{4}\)A figura ilustra possíveis conjuntos de soluções para um sistema de equações envolvendo um círculo e uma linha.
- Sem solução - A linha não cruza o círculo.
- Uma solução - A linha é tangente ao círculo e cruza o círculo em exatamente um ponto.
- Duas soluções - A linha cruza o círculo e o cruza em dois pontos.

Figura\(\PageIndex{4}\)
- Resolva a equação linear para uma das variáveis.
- Substitua a expressão obtida na etapa um na equação do círculo.
- Resolva a variável restante.
- Verifique suas soluções nas duas equações.
Encontre a interseção de um determinado círculo e a linha dada por substituição.
\[\begin{align*} x^2+y^2 &= 5\nonumber \\ y &= 3x−5 \nonumber \end{align*}\]
Solução
Uma das equações já foi resolvida para\(y\). Vamos substituir\(y=3x−5\) a circunferência na equação.
\[\begin{align*} x^2+{(3x−5)}^2 &= 5\nonumber \\ x^2+9x^2−30x+25 &= 5\nonumber \\ 10x^2−30x+20 &= 0 \end{align*} \]
Agora, nós fatoramos e resolvemos\(x\).
\[\begin{align*} 10(x2−3x+2) &= 0\nonumber \\ 10(x−2)(x−1) &= 0\nonumber \\ x &= 2\nonumber \\ x &= 1 \nonumber \end{align*}\]
Substitua os dois\(x\) valores na equação linear original para resolver\(y\).
\[\begin{align*} y &= 3(2)−5\nonumber \\ &= 1\nonumber \\ y &= 3(1)−5\nonumber \\ &= −2 \nonumber \end{align*}\]
A linha cruza o círculo em\((2,1)\) e\((1,−2)\), o que pode ser verificado substituindo esses\((x,y)\) valores nas duas equações originais (Figura\(\PageIndex{5}\)).
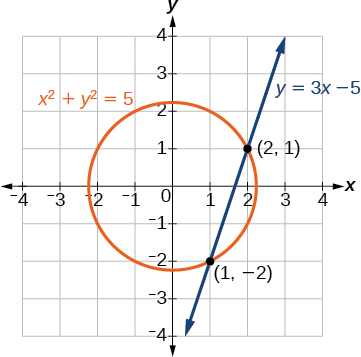
Figura\(\PageIndex{5}\)
Resolva o sistema de equações não lineares.
\[\begin{align*} x^2+y^2 &= 10\nonumber \\ x−3y &= −10 \nonumber \end{align*}\]
- Resposta
-
\((−1,3)\)
Resolvendo um sistema de equações não lineares usando eliminação
Vimos que a substituição geralmente é o método preferido quando um sistema de equações inclui uma equação linear e uma equação não linear. No entanto, quando ambas as equações no sistema têm variáveis semelhantes de segundo grau, resolvê-las usando a eliminação por adição geralmente é mais fácil do que a substituição. Geralmente, a eliminação é um método muito mais simples quando o sistema envolve apenas duas equações em duas variáveis (um sistema de dois por dois), em vez de um sistema de três por três, pois há menos etapas. Como exemplo, investigaremos os possíveis tipos de soluções ao resolver um sistema de equações representando um círculo e uma elipse.
\(\PageIndex{6}\)A figura ilustra possíveis conjuntos de soluções para um sistema de equações envolvendo um círculo e uma elipse.
- Sem solução - O círculo e a elipse não se cruzam. Uma forma está dentro da outra ou do círculo e a elipse está a uma distância da outra.
- Uma solução - O círculo e a elipse são tangentes um ao outro e se cruzam exatamente em um ponto.
- Duas soluções - O círculo e a elipse se cruzam em dois pontos.
- Três soluções - O círculo e a elipse se cruzam em três pontos.
- Quatro soluções - O círculo e a elipse se cruzam em quatro pontos.
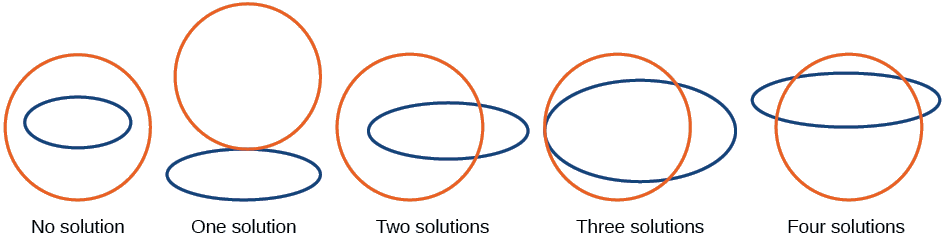
Figura\(\PageIndex{6}\)
Resolva o sistema de equações não lineares.
\[\begin{align*} x^2+y^2 &= 26 &(1)\nonumber \\ 3x^2+25y^2 &= 100 & (2) \nonumber \end{align*}\]
Solução
Vamos começar multiplicando a equação (1) por\(−3\) e adicionando-a à equação (2).
\[\begin{align*} (−3)(x^2+y^2) = (−3)(26)&\nonumber \\ −3x^2−3y^2 = −78 &\nonumber \\ \underline{3x^2+25y^2=100}&\nonumber \\ 22y^2=22& \nonumber \end{align*}\]
Depois de somarmos as duas equações, resolvemos para\(y\).
\[\begin{align*} y^2 &= 1\nonumber \\ y &= \pm \sqrt{1}=\pm 1 \nonumber \end{align*}\]
\(y=\pm 1\)Substitua em uma das equações e resolva\(x\).
\[\begin{align*} x^2+{(1)}^2 &= 26\nonumber \\ x^2+1 &= 26\nonumber \\ x^2 &= 25\nonumber \\ x &= \pm \sqrt{25}=\pm 5\nonumber \\ x^2+{(−1)}^2 &= 26\nonumber \\ x^2+1 &= 26\nonumber \\ x^2 &= \pm \sqrt{25}=\pm 5 \nonumber \end{align*}\]
Há quatro soluções:\((5,1)\)\((−5,1)\),\((5,−1)\),\((−5,−1)\) e. Veja a Figura\(\PageIndex{7}\).
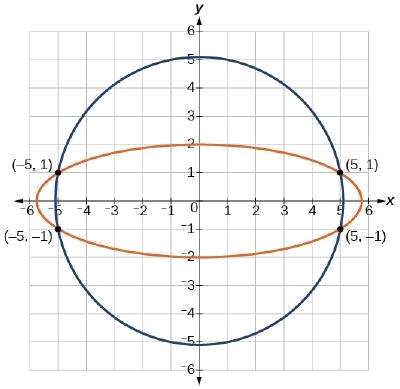
Figura\(\PageIndex{7}\)
Encontre o conjunto de soluções para um determinado sistema de equações não lineares.
\[\begin{align*} 4x^2+y^2 &= 13\nonumber \\ x^2+y^2 &= 10 \nonumber \end{align*}\]
- Resposta
-
\({(1,3),(1,−3),(−1,3),(−1,−3)}\)
Representação gráfica de uma desigualdade não linear
Todas as equações nos sistemas que encontramos até agora envolveram igualdades, mas também podemos encontrar sistemas que envolvem desigualdades. Já aprendemos a representar graficamente as desigualdades lineares representando graficamente a equação correspondente e, em seguida, sombreando a região representada pelo símbolo de desigualdade. Agora, seguiremos etapas semelhantes para representar graficamente uma desigualdade não linear para que possamos aprender a resolver sistemas de desigualdades não lineares. Uma desigualdade não linear é uma desigualdade que contém uma expressão não linear. Representar graficamente uma desigualdade não linear é muito parecido com representar graficamente uma desigualdade linear.
Lembre-se de que quando a desigualdade é maior ou menor que\(y<a\), o gráfico é desenhado com uma linha tracejada.\(y>a\) Quando a desigualdade é maior ou igual a\(y≥a\), ou menor ou igual a\(y≤a\), o gráfico é desenhado com uma linha sólida. Os gráficos criarão regiões no plano e testaremos cada região em busca de uma solução. Se um ponto na região funcionar, toda a região funcionará. Essa é a região que sombreamos (Figura\(\PageIndex{8}\)).
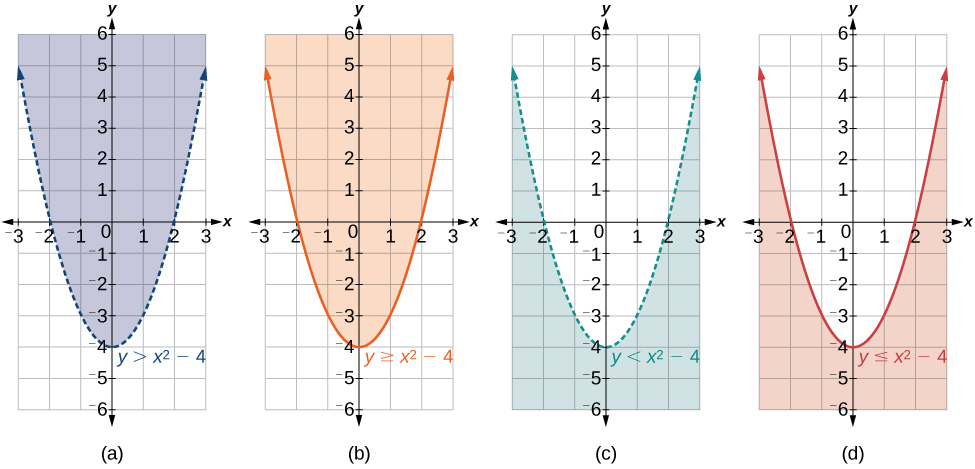
Figura\(\PageIndex{8}\): (a) um exemplo de\(y>a\); (b) um exemplo de\(y≥a\); (c) um exemplo de\(y<a\); (d) um exemplo de\(y≤a\)
- Faça um gráfico da parábola como se fosse uma equação. Esse é o limite da região que é o conjunto de soluções.
- Se o limite estiver incluído na região (o operador é\(≤\) ou\(≥\)), a parábola é representada graficamente como uma linha sólida.
- Se o limite não estiver incluído na região (o operador é\(<\) ou\(>\)), a parábola será representada graficamente como uma linha tracejada.
- Teste um ponto em uma das regiões para determinar se ele satisfaz a declaração de desigualdade. Se a afirmação for verdadeira, o conjunto de soluções é a região que inclui o ponto. Se a afirmação for falsa, o conjunto de soluções será a região do outro lado da linha limite.
- Sombreie a região que representa o conjunto de soluções.
Faça um gráfico da desigualdade\(y>x^2+1\).
Solução
Primeiro, represente graficamente a equação correspondente\(y=x^2+1\). Como\(y>x^2+1\) tem um símbolo maior que, desenhamos o gráfico com uma linha tracejada. Em seguida, escolhemos pontos para testar dentro e fora da parábola. Vamos testar os pontos
\((0,2)\)\((2,0)\)e. Um ponto está claramente dentro da parábola e o outro ponto está claramente fora.
\[\begin{align*} y &> x^2+1\nonumber \\ 2 &> (0)^2+1\nonumber \\ 2 &>1 & \text{True}\nonumber \\\nonumber \\\nonumber \\ 0 &> (2)^2+1\nonumber \\ 0 &> 5 & \text{False} \nonumber \end{align*}\]
O gráfico é mostrado na Figura\(\PageIndex{9}\). Podemos ver que o conjunto de soluções consiste em todos os pontos dentro da parábola, mas não no gráfico em si.
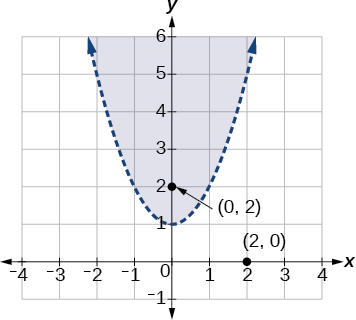
Figura\(\PageIndex{9}\)
Representação gráfica de um sistema de desigualdades não lineares
Agora que aprendemos a representar graficamente desigualdades não lineares, podemos aprender a representar graficamente sistemas de desigualdades não lineares. Um sistema de desigualdades não lineares é um sistema de duas ou mais desigualdades em duas ou mais variáveis contendo pelo menos uma desigualdade que não seja linear. Representar graficamente um sistema de desigualdades não lineares é semelhante à representação gráfica de um sistema de desigualdades lineares. A diferença é que nosso gráfico pode resultar em mais regiões sombreadas que representam uma solução do que encontramos em um sistema de desigualdades lineares. A solução para um sistema não linear de desigualdades é a região do gráfico onde as regiões sombreadas do gráfico de cada desigualdade se sobrepõem, ou onde as regiões se cruzam, chamada de região viável.
- Encontre os pontos de interseção resolvendo o sistema correspondente de equações não lineares.
- Representar graficamente as equações não lineares.
- Encontre as regiões sombreadas de cada desigualdade.
- Identifique a região viável como a interseção das regiões sombreadas de cada desigualdade ou o conjunto de pontos comuns a cada desigualdade.
Representar graficamente o sistema de desigualdades fornecido.
\[\begin{align*} x^2−y &≤ 0\nonumber \\ 2x^2+y &≤ 12 \nonumber \end{align*}\]
Solução
Essas duas equações são claramente parábolas. Podemos encontrar os pontos de interseção pelo processo de eliminação: Adicione as duas equações e a variável\(y\) será eliminada. Então resolvemos por\(x\).
\[\begin{align*} x^2−y = 0&\nonumber \\ \underline{2x^2+y=12}&\nonumber \\ 3x^2=12&\nonumber \\ x^2=4 &\nonumber \\ x=\pm 2 & \nonumber \end{align*}\]
Substitua\(x\) os valores -em uma das equações e resolva por\(y\).
\[\begin{align*} x^2−y &= 0\nonumber \\ {(2)}^2−y &= 0\nonumber \\ 4−y &= 0\nonumber \\ y &= 4\nonumber \\\nonumber \\ {(−2)}^2−y &= 0\nonumber \\ 4−y &= 0\nonumber \\ y &= 4 \nonumber \end{align*}\]
Os dois pontos de interseção são\((2,4)\)\((−2,4)\) e. Observe que as equações podem ser reescritas da seguinte forma.
\[\begin{align*} x^2-y & ≤ 0\nonumber \\ x^2 &≤ y\nonumber \\ y &≥ x^2\nonumber \\\nonumber \\\nonumber \\ 2x^2+y &≤ 12\nonumber \\ y &≤ −2x^2+12 \nonumber \end{align*}\]
Faça um gráfico de cada desigualdade. Veja a Figura\(\PageIndex{10}\). A região viável é a região entre as duas equações delimitada\(2x^2+y≤12\) na parte superior e\(x^2−y≤0\) na parte inferior.
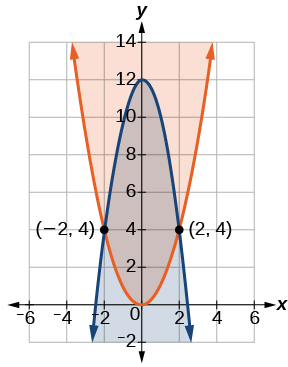
Figura\(\PageIndex{10}\)
Representar graficamente o sistema de desigualdades fornecido.
\[\begin{align*} y &≥ x^2−1\nonumber \\ x−y &≥ −1 \nonumber \end{align*}\]
- Resposta
-
Sombreie a área delimitada pelas duas curvas, acima da quadrática e abaixo da linha.
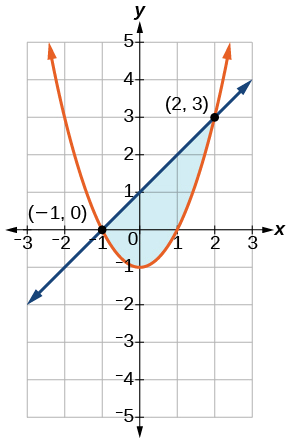
Figura\(\PageIndex{11}\)
Acesse esses recursos on-line para obter instruções e práticas adicionais com equações não lineares.
Conceitos chave
- Existem três tipos possíveis de soluções para um sistema de equações representando uma reta e uma parábola: (1) sem solução, a reta não cruza a parábola; (2) uma solução, a reta é tangente à parábola; e (3) duas soluções, a linha cruza a parábola em dois pontos. Veja o exemplo\(\PageIndex{1}\).
- Existem três tipos possíveis de soluções para um sistema de equações representando um círculo e uma reta: (1) sem solução, a linha não cruza o círculo; (2) uma solução, a reta é tangente à parábola; (3) duas soluções, a linha cruza o círculo em dois pontos. Veja o exemplo\(\PageIndex{2}\).
- Existem cinco tipos possíveis de soluções para o sistema de equações não lineares representando uma elipse e um círculo:
(1) sem solução, o círculo e a elipse não se cruzam; (2) uma solução, o círculo e a elipse são tangentes um ao outro; (3) duas soluções, o círculo e o a elipse se cruzam em dois pontos; (4) três soluções, o círculo e a elipse se cruzam em três lugares; (5) quatro soluções, o círculo e a elipse se cruzam em quatro pontos. Veja o exemplo\(\PageIndex{3}\). - Uma desigualdade é representada graficamente da mesma forma que uma equação, exceto por > ou <, desenhamos uma linha tracejada e sombreamos a região que contém o conjunto de soluções. Veja o exemplo\(\PageIndex{4}\).
- As desigualdades são resolvidas da mesma forma que as igualdades, mas as soluções para sistemas de desigualdades devem satisfazer ambas as desigualdades. Veja o exemplo\(\PageIndex{5}\).


