9.2: Sistemas de equações lineares - três variáveis
- Page ID
- 189156
- Resolva sistemas de três equações em três variáveis.
- Identifique sistemas inconsistentes de equações contendo três variáveis.
- Expresse a solução de um sistema de equações dependentes contendo três variáveis.
John recebeu uma herança\($12,000\) que dividiu em três partes e investiu de três maneiras: em um fundo do mercado monetário pagando juros\(3\%\) anuais; em títulos municipais pagando juros\(4\%\) anuais; e em fundos mútuos pagando juros\(7\%\) anuais. John investiu\($4,000\) mais em fundos municipais do que em títulos municipais. Ele ganhou juros\($670\) no primeiro ano. Quanto John investiu em cada tipo de fundo?

Figura\(\PageIndex{1}\): (crédito: “Elembis”, Wikimedia Commons)
Entender a abordagem correta para configurar problemas como este faz com que encontrar uma solução seja uma questão de seguir um padrão. Resolveremos esse e outros problemas semelhantes envolvendo três equações e três variáveis nesta seção. Fazer isso usa técnicas semelhantes às usadas para resolver sistemas de duas equações em duas variáveis. No entanto, encontrar soluções para sistemas de três equações requer um pouco mais de organização e um toque de ginástica visual.
Resolvendo sistemas de três equações em três variáveis
Para resolver sistemas de equações em três variáveis, conhecidos como sistemas três por três, a principal ferramenta que usaremos é chamada de eliminação gaussiana, em homenagem ao prolífico matemático alemão Karl Friedrich Gauss. Embora não haja uma ordem definitiva na qual as operações devem ser executadas, existem diretrizes específicas sobre quais tipos de movimentos podem ser feitos. Podemos numerar as equações para acompanhar as etapas que aplicamos. O objetivo é eliminar uma variável de cada vez para obter a forma triangular superior, a forma ideal para um sistema de três por três porque permite a substituição reversa direta para encontrar uma solução\((x,y,z)\), que chamamos de tripla ordenada. Um sistema na forma triangular superior tem a seguinte aparência:
\[\begin{align*} Ax+By+Cz &= D \nonumber \\[4pt] Ey+Fz &= G \nonumber \\[4pt] Hz &= K \nonumber \end{align*} \nonumber\]
A terceira equação pode ser resolvida e\(z\), em seguida, substituímos novamente por encontrar\(y\)\(x\) e. Para escrever o sistema na forma triangular superior, podemos realizar as seguintes operações:
- Troque a ordem de quaisquer duas equações.
- Multiplique os dois lados de uma equação por uma constante diferente de zero.
- Adicione um múltiplo diferente de zero de uma equação a outra equação.
A solução definida para um sistema de três por três é uma tripla ordenada\({(x,y,z)}\). Graficamente, o triplo ordenado define o ponto que é a interseção de três planos no espaço. Você pode visualizar essa interseção imaginando qualquer canto em uma sala retangular. Um canto é definido por três planos: duas paredes adjacentes e o piso (ou teto). Qualquer ponto em que duas paredes e o piso se encontram representa a interseção de três planos.
A figura\(\PageIndex{2}\) e a figura\(\PageIndex{3}\) ilustram possíveis cenários de solução para sistemas de três por três.
- Os sistemas que têm uma única solução são aqueles que, após a eliminação, resultam em um conjunto de soluções que consiste em uma tripla ordenada\({(x,y,z)}\). Graficamente, o triplo ordenado define um ponto que é a interseção de três planos no espaço.
- Sistemas que têm um número infinito de soluções são aqueles que, após a eliminação, resultam em uma expressão sempre verdadeira, como\(0=0\). Graficamente, um número infinito de soluções representa uma linha ou plano coincidente que serve como a interseção de três planos no espaço.
- Sistemas que não têm solução são aqueles que, após a eliminação, resultam em uma afirmação que é uma contradição, como\(3=0\). Graficamente, um sistema sem solução é representado por três planos sem nenhum ponto em comum.

Figura\(\PageIndex{2}\): (a) Três planos se cruzam em um único ponto, representando um sistema três por três com uma única solução. (b) Três planos se cruzam em uma linha, representando um sistema três por três com soluções infinitas.

Figura\(\PageIndex{3}\): Todas as três figuras representam sistemas de três por três sem solução. (a) Os três planos se cruzam, mas não em um ponto comum. (b) Dois dos planos são paralelos e se cruzam com o terceiro plano, mas não um com o outro. (c) Todos os três planos são paralelos, então não há ponto de interseção.
Determine se o triplo solicitado\((3,−2,1)\) é uma solução para o sistema.
\[\begin{align*} x+y+z &= 2 \nonumber \\[4pt] 6x−4y+5z &= 31 \nonumber \\[4pt] 5x+2y+2z &= 13 \nonumber \end{align*} \nonumber\]
Solução
Verificaremos cada equação substituindo os valores do triplo ordenado por\( x,y\),\(z\) e.
\[\begin{array}{rrr} { \text{} \nonumber \\[4pt] x+y+z=2 \nonumber \\[4pt] (3)+(−2)+(1)=2 \nonumber \\[4pt] \text{True}} & {6x−4y+5z=31 \nonumber \\[4pt] 6(3)−4(−2)+5(1)=31 \nonumber \\[4pt] 18+8+5=31 \nonumber \\[4pt] \text{True} } & { 5x+2y+2z = 13 \nonumber \\[4pt] 5(3)+2(−2)+2(1)=13 \nonumber \\[4pt] 15−4+2=13 \nonumber \\[4pt] \text{True}} \end{array}\]
O triplo encomendado\((3,−2,1)\) é de fato uma solução para o sistema.
- Escolha qualquer par de equações e resolva uma variável.
- Escolha outro par de equações e resolva a mesma variável.
- Você criou um sistema de duas equações em duas incógnitas. Resolva o sistema resultante de dois por dois.
- Substitua novamente as variáveis conhecidas em qualquer uma das equações originais e resolva a variável ausente.
Encontre uma solução para o seguinte sistema:
\[\begin{align} x−2y+3z=9 \; &(1) \nonumber \\[4pt] −x+3y−z=−6 \; &(2) \nonumber \\[4pt] 2x−5y+5z=17 \; &(3) \nonumber \end{align} \nonumber\]
Solução
Sempre haverá várias opções sobre por onde começar, mas o primeiro passo mais óbvio aqui é eliminar\(x\) adicionando as equações (1) e (2).
\[\begin{align} x−2y+3z=9 \; \; &(1) \nonumber \\[4pt] \underline{−x+3y−z=−6 }\; \; &(2) \nonumber \\[4pt] y+2z=3 \;\; &(3) \nonumber \end{align} \nonumber\]
A segunda etapa é multiplicar a equação (1)\(−2\) e adicionar o resultado à equação (3). Essas duas etapas eliminarão a variável\(x\).
\[\begin{align} −2x+4y−6z=−18\; &(1) \;\;\;\; \text{ multiplied by }−2 \nonumber \\[4pt] \underline{2x−5y+5z=17} \; & (3) \nonumber \\[4pt]−y−z=−1 \; &(5) \nonumber \end{align} \nonumber\]
Nas equações (4) e (5), criamos um novo sistema dois por dois. Podemos resolver isso\(z\) adicionando as duas equações.
\[\begin{align} y+2z=3 \; &(4) \nonumber \\[4pt] \underline{−y−z=−1} \; & (5) \nonumber \\[4pt] z=2 \; & (6) \nonumber \end{align} \nonumber\]
Escolhendo uma equação de cada novo sistema, obtemos a forma triangular superior:
\[\begin{align} x−2y+3z=9 \; &(1) \nonumber \\[4pt] y+2z =3 \; &(4) \nonumber \\[4pt] z=2 \; &(6) \nonumber \end{align} \nonumber\]
Em seguida, substituímos novamente\(z=2\) na equação (4) e resolvemos por\(y\).
\[\begin{align} y+2(2) &=3 \nonumber \\[4pt] y+4 &= 3 \nonumber \\[4pt] y &= −1 \nonumber \end{align} \nonumber\]
Finalmente, podemos voltar a substituir\(z=2\) e\(y=−1\) entrar na equação (1). Isso produzirá a solução para\(x\).
\[\begin{align} x−2(−1)+3(2) &= 9 \nonumber \\[4pt] x+2+6 &=9 \nonumber \\[4pt] x &= 1 \nonumber \end{align} \nonumber\]
A solução é o triplo pedido\((1,−1,2)\). Veja a Figura\(\PageIndex{4}\).
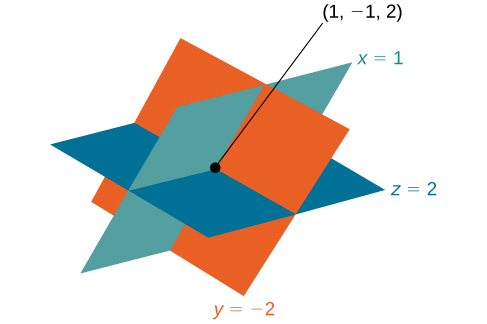
Figura\(\PageIndex{4}\)
No problema apresentado no início da seção, John investiu sua herança\($12,000\) em três fundos diferentes: parte em um fundo do mercado monetário pagando\(3\%\) juros anualmente; parte em títulos municipais pagando\(4\%\) anualmente; e o restante em fundos mútuos pagando\(7\%\) anualmente. John investiu\($4,000\) mais em fundos mútuos do que em títulos municipais. O total de juros ganhos em um ano foi\($670\). Quanto ele investiu em cada tipo de fundo?
Solução
Para resolver esse problema, usamos todas as informações fornecidas e configuramos três equações. Primeiro, atribuímos uma variável a cada um dos três valores de investimento:
\[\begin{align} x &= \text{amount invested in money-market fund} \nonumber \\[4pt] y &= \text{amount invested in municipal bonds} \nonumber \\[4pt] z &= \text{amount invested in mutual funds} \nonumber \end{align} \nonumber\]
A primeira equação indica que a soma dos três valores principais é\($12,000\).
\[x+y+z=12,000 \nonumber\]
Formamos a segunda equação de acordo com a informação de que John investiu\($4,000\) mais em fundos mútuos do que em títulos municipais.
\[z=y+4,000 \nonumber\]
A terceira equação mostra que o valor total de juros ganhos de cada fundo é igual\($670\).
\[0.03x+0.04y+0.07z=670 \nonumber\]
Em seguida, escrevemos as três equações como um sistema.
\[\begin{align} x+y+z &=12,000 \nonumber \\[4pt] −y+z &= 4,000 \nonumber \\[4pt] 0.03x+0.04y+0.07z &= 670 \nonumber \end{align} \nonumber\]
Para simplificar os cálculos, podemos multiplicar a terceira equação por\(100\). Assim,
\[\begin{align} x+y+z &=12,000 \; &(1) \nonumber \\[4pt] −y+z &= 4,000 \; &(2) \nonumber \\[4pt] 3x+4y+7z &= 67,000 \; &(3) \nonumber \end{align} \nonumber\]
Etapa 1. Troque a equação (2) e a equação (3) para que as duas equações com três variáveis se alinhem.
\[\begin{align} x+y+z &= 12,000 \nonumber \\[4pt] 3x+4y+7z &= 67,000 \nonumber \\[4pt] −y+z &= 4,000 \nonumber \end{align} \nonumber\]
Etapa 2. Multiplique a equação (1) por\(−3\) e adicione à equação (2). Escreva o resultado como linha 2.
\[\begin{align} x+y+z &= 12,000 \nonumber \\[4pt] y+4z &= 31,000 \nonumber \\[4pt] −y+z &= 4,000 \nonumber \end{align} \nonumber\]
Etapa 3. Adicione a equação (2) à equação (3) e escreva o resultado como equação (3).
\[\begin{align} x+y+z &= 12,000 \nonumber \\[4pt] y+4z &= 31,000 \nonumber \\[4pt] 5z &= 35,000 \nonumber \end{align} \nonumber\]
Etapa 4. Resolva para\(z\) na equação (3). Substitua novamente esse valor na equação (2) e resolva por\(y\). Em seguida, substitua os valores por\(z\) e\(y\) na equação (1) e resolva por\(x\).
\[\begin{align} 5z &= 35,000 \nonumber \\[4pt] z &= 7,000 \nonumber \\[4pt] \nonumber \\[4pt] y+4(7,000) &= 31,000 \nonumber \\[4pt] y &=3,000 \nonumber \\[4pt] \nonumber \\[4pt] x+3,000+7,000 &= 12,000 \nonumber \\[4pt] x &= 2,000 \nonumber \end{align} \nonumber\]
John investiu\($2,000\) em um fundo do mercado monetário,\($3,000\) em títulos municipais e\($7,000\) em fundos mútuos.
Resolva o sistema de equações em três variáveis.
\[\begin{align} 2x+y−2z &= −1 \nonumber \\[4pt] 3x−3y−z &= 5 \nonumber \\[4pt] x−2y+3z &= 6 \nonumber \end{align} \nonumber\]
- Responda
-
\((1,−1,1)\)
Identificação de sistemas inconsistentes de equações contendo três variáveis
Assim como com sistemas de equações em duas variáveis, podemos encontrar um sistema inconsistente de equações em três variáveis, o que significa que ele não tem uma solução que satisfaça todas as três equações. As equações podem representar três planos paralelos, dois planos paralelos e um plano de interseção, ou três planos que cruzam os outros dois, mas não no mesmo local. O processo de eliminação resultará em uma declaração falsa, como\(3=7\) ou alguma outra contradição.
Resolva o sistema a seguir.
\[\begin{align} x−3y+z &=4 \label{4.1}\\[4pt] −x+2y−5z &=3 \label{4.2} \\[4pt] 5x−13y+13z &=8 \label{4.3} \end{align} \nonumber\]
Solução
Observando os coeficientes de\(x\), podemos ver que podemos eliminar\(x\) adicionando a Equação\ ref {4.1} à Equação\ ref {4.2}.
\[\begin{align} x−3y+z = 4 &(1) \nonumber \\[4pt] \underline{−x+2y−5z=3} & (2) \nonumber \\[4pt] −y−4z =7 & (4) \nonumber \end{align} \nonumber\]
Em seguida, multiplicamos a equação (1) por\(−5\) e a adicionamos à equação (3).
\[\begin{align} −5x+15y−5z =−20 & (1) \;\;\;\;\; \text{multiplied by }−5 \nonumber \\[4pt] \underline{5x−13y+13z=8} &(3) \nonumber \\[4pt] 2y+8z=−12 &(5) \nonumber \end{align} \nonumber\]
Em seguida, multiplicamos a equação (4) por 2 e a adicionamos à equação (5).
\[\begin{align} −2y−8z=14 & (4) \;\;\;\;\; \text{multiplied by }2 \nonumber \\[4pt] \underline{2y+8z=−12} & (5) \nonumber \\[4pt] 0=2 & \nonumber \end{align} \nonumber\]
A equação final\(0=2\) é uma contradição, então concluímos que o sistema de equações é inconsistente e, portanto, não tem solução.
Análise
Nesse sistema, cada plano cruza os outros dois, mas não no mesmo local. Portanto, o sistema é inconsistente.
Resolva o sistema de três equações em três variáveis.
\[\begin{align} x+y+z &= 2 \nonumber \\[4pt] y−3z &=1 \nonumber \\[4pt] 2x+y+5z &=0 \nonumber \end{align} \nonumber\]
- Responda
-
Sem solução.
Expressando a solução de um sistema de equações dependentes contendo três variáveis
Sabemos, trabalhando com sistemas de equações em duas variáveis, que um sistema de equações dependente tem um número infinito de soluções. O mesmo vale para sistemas de equações dependentes em três variáveis. Um número infinito de soluções pode resultar de várias situações. Os três planos podem ser iguais, então uma solução para uma equação será a solução para as outras duas equações. Todas as três equações podem ser diferentes, mas elas se cruzam em uma linha, que tem soluções infinitas. Ou duas das equações podem ser iguais e cruzar a terceira em uma linha.
Encontre a solução para o sistema dado de três equações em três variáveis.
\[\begin{align} 2x+y−3z &= 0 &(1) \nonumber \\[4pt] 4x+2y−6z &=0 &(2) \nonumber \\[4pt] x−y+z &= 0 &(3) \nonumber \end{align} \nonumber\]
Solução
Primeiro, podemos multiplicar a equação (1) por\(−2\) e adicioná-la à equação (2).
\[\begin{align} −4x−2y+6z =0 & (1) \;\;\;\;\; \text{multiplied by }−2 \nonumber \\[4pt] \underline{4x+2y−6z=0} & (2) \nonumber \\[4pt] 0=0& \nonumber \end{align} \nonumber\]
Não precisamos prosseguir. O resultado que obtemos é uma identidade\(0=0\), que nos diz que esse sistema tem um número infinito de soluções. Existem outras maneiras de começar a resolver esse sistema, como multiplicar a equação (3) por\(−2\) e adicioná-la à equação (1). Em seguida, executamos as mesmas etapas acima e encontramos o mesmo resultado,\(0=0\).
Quando um sistema é dependente, podemos encontrar expressões gerais para as soluções. Adicionando equações (1) e (3), temos
\[\begin{align} 2x+y−3z &= 0 \nonumber \\[4pt]x−y+z &= 0 \nonumber \\[4pt] 3x−2z &= 0 \nonumber \end{align} \nonumber\]
Em seguida, resolvemos a equação resultante para\(z\).
\[\begin{align} 3x−2z &= 0 \nonumber \\[4pt] z &= \dfrac{3}{2}x \nonumber \end{align} \nonumber\]
Substituímos novamente a expressão por\(z\) em uma das equações e resolvemos por\(y\).
\[\begin{align} 2x+y−3 (\dfrac{3}{2}x) &= 0 \nonumber \\[4pt] 2x+y−\dfrac{9}{2}x &= 0 \nonumber \\[4pt] y &= \dfrac{9}{2}x−2x \nonumber \\[4pt] y &=\dfrac{5}{2}x \nonumber \end{align} \nonumber\]
Portanto, a solução geral é\(\left(x,\dfrac{5}{2}x,\dfrac{3}{2}x\right)\). Nesta solução,\(x\) pode ser qualquer número real. Os valores de\(y\) e\(z\) dependem do valor selecionado para\(x\).
Análise
Conforme mostrado na Figura\(\PageIndex{5}\), dois dos planos são iguais e cruzam o terceiro plano em uma linha. O conjunto de soluções é infinito, pois todos os pontos ao longo da linha de interseção satisfarão todas as três equações.

Figura\(\PageIndex{5}\)
Não, você pode escrever a solução genérica em termos de qualquer uma das variáveis, mas é comum escrevê-la em termos de\(x\) e, se necessário\(x\),\(y\) e.
Resolva o sistema a seguir.
\[\begin{align} x+y+z &= 7 \nonumber \\[4pt] 3x−2y−z &= 4 \nonumber \\[4pt] x+6y+5z &= 24 \nonumber \end{align} \nonumber\]
- Responda
-
Número infinito de soluções do formulário\((x,4x−11,−5x+18)\).
Acesse esses recursos on-line para obter instruções e práticas adicionais com sistemas de equações em três variáveis.
Conceitos-chave
- Um conjunto de soluções é um triplo ordenado {(x, y, z)} que representa a interseção de três planos no espaço. Veja o exemplo\(\PageIndex{1}\).
- Um sistema de três equações em três variáveis pode ser resolvido usando uma série de etapas que força a eliminação de uma variável. As etapas incluem trocar a ordem das equações, multiplicar os dois lados de uma equação por uma constante diferente de zero e adicionar um múltiplo diferente de zero de uma equação a outra equação. Veja o exemplo\(\PageIndex{2}\).
- Sistemas de três equações em três variáveis são úteis para resolver muitos tipos diferentes de problemas do mundo real. Veja o exemplo\(\PageIndex{3}\).
- Um sistema de equações em três variáveis é inconsistente se não houver solução. Depois de realizar operações de eliminação, o resultado é uma contradição. Veja o exemplo\(\PageIndex{4}\).
- Sistemas de equações em três variáveis que são inconsistentes podem resultar de três planos paralelos, dois planos paralelos e um plano de interseção, ou três planos que cruzam os outros dois, mas não no mesmo local.
- Um sistema de equações em três variáveis depende se tiver um número infinito de soluções. Depois de realizar as operações de eliminação, o resultado é uma identidade. Veja o exemplo\(\PageIndex{5}\).
- Sistemas de equações em três variáveis que são dependentes podem resultar de três planos idênticos, três planos se cruzando em uma linha ou dois planos idênticos que cruzam o terceiro em uma linha.


