9.1: Sistemas de equações lineares - duas variáveis
- Page ID
- 189162
- Resolva sistemas de equações representando graficamente.
- Resolva sistemas de equações por substituição.
- Resolva sistemas de equações por adição.
- Identifique sistemas inconsistentes de equações contendo duas variáveis.
- Expresse a solução de um sistema de equações dependentes contendo duas variáveis.
Um fabricante de skates apresenta uma nova linha de pranchas. O fabricante acompanha seus custos, que é o valor gasto para produzir as placas, e sua receita, que é o valor que ele ganha com a venda de suas placas. Como a empresa pode determinar se está lucrando com sua nova linha? Quantos skates devem ser produzidos e vendidos antes que o lucro seja possível? Nesta seção, consideraremos equações lineares com duas variáveis para responder a essas e outras perguntas similares.

Introdução aos sistemas de equações
Para investigar situações como a do fabricante do skate, precisamos reconhecer que estamos lidando com mais de uma variável e provavelmente com mais de uma equação. Um sistema de equações lineares consiste em duas ou mais equações lineares compostas por duas ou mais variáveis, de forma que todas as equações no sistema sejam consideradas simultaneamente. Para encontrar a solução única para um sistema de equações lineares, precisamos encontrar um valor numérico para cada variável no sistema que satisfaça todas as equações no sistema ao mesmo tempo. Alguns sistemas lineares podem não ter uma solução e outros podem ter um número infinito de soluções. Para que um sistema linear tenha uma solução única, deve haver pelo menos tantas equações quanto variáveis. Mesmo assim, isso não garante uma solução única.
Nesta seção, examinaremos sistemas de equações lineares em duas variáveis, que consistem em duas equações que contêm duas variáveis diferentes. Por exemplo, considere o seguinte sistema de equações lineares em duas variáveis.
\[\begin{align*} 2x+y &= 15 \\ 3x–y &= 5 \end{align*}\]
A solução para um sistema de equações lineares em duas variáveis é qualquer par ordenado que satisfaça cada equação de forma independente. Neste exemplo, o par ordenado\((4,7)\) é a solução para o sistema de equações lineares. Podemos verificar a solução substituindo os valores em cada equação para ver se o par ordenado satisfaz as duas equações. Em breve, investigaremos métodos para encontrar essa solução, se ela existir.
\[\begin{align*} 2(4)+(7) &=15 \text{ True} \\ 3(4)−(7) &= 5 \text{ True} \end{align*}\]
Além de considerar o número de equações e variáveis, podemos categorizar sistemas de equações lineares pelo número de soluções. Um sistema consistente de equações tem pelo menos uma solução. Um sistema consistente é considerado um sistema independente se tiver uma única solução, como o exemplo que acabamos de explorar. As duas linhas têm inclinações diferentes e se cruzam em um ponto do plano. Um sistema consistente é considerado um sistema dependente se as equações tiverem a mesma inclinação e os mesmos interceptos y. Em outras palavras, as linhas coincidem, então as equações representam a mesma linha. Cada ponto na linha representa um par de coordenadas que satisfaz o sistema. Assim, há um número infinito de soluções.
Outro tipo de sistema de equações lineares é um sistema inconsistente, que é aquele em que as equações representam duas linhas paralelas. As linhas têm a mesma inclinação e diferentes interceptações em y. Não há pontos comuns às duas linhas; portanto, não há solução para o sistema.
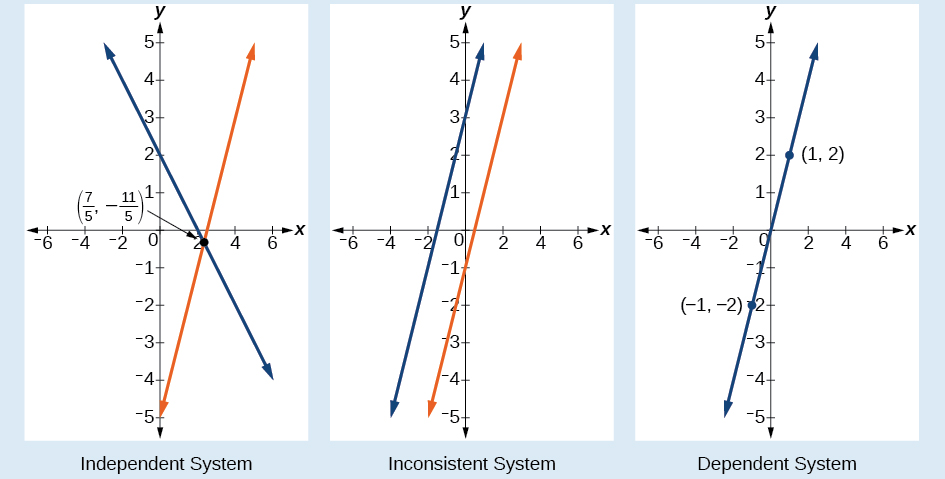
Existem três tipos de sistemas de equações lineares em duas variáveis e três tipos de soluções.
- Um sistema independente tem exatamente um par de soluções\((x,y)\). O ponto em que as duas linhas se cruzam é a única solução.
- Um sistema inconsistente não tem solução. Observe que as duas linhas são paralelas e nunca se cruzarão.
- Um sistema dependente tem infinitas soluções. As linhas são coincidentes. Eles são a mesma linha, então cada par de coordenadas na linha é uma solução para ambas as equações.
A figura\(\PageIndex{2}\) compara representações gráficas de cada tipo de sistema.
- Substitua o par ordenado em cada equação no sistema.
- Determine se as afirmações verdadeiras resultam da substituição em ambas as equações; em caso afirmativo, o par ordenado é uma solução.
Determine se o par ordenado\((5,1)\) é uma solução para o determinado sistema de equações.
\[\begin{align*} x+3y &= 8 \\ 2x−9 &= y \end{align*}\]
Solução
Substitua o par ordenado\((5,1)\) em ambas as equações.
\[ \begin{align*} (5)+3(1) &= 8 \\ 8 &= 8 \text{ True} \\ 2(5)−9 &= (1) \\ 1 &= 1 \text{ True} \end{align*}\]
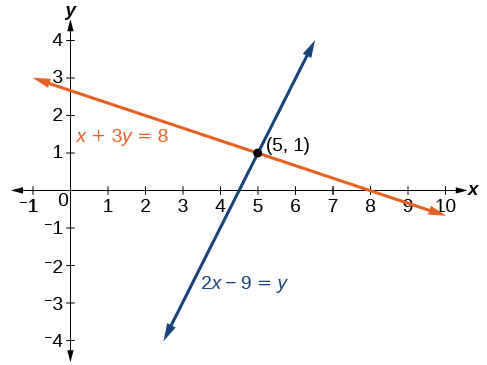
O par ordenado\((5,1)\) satisfaz as duas equações, então é a solução para o sistema.
Análise
Podemos ver a solução claramente traçando o gráfico de cada equação. Como a solução é um par ordenado que satisfaz as duas equações, é um ponto em ambas as retas e, portanto, o ponto de interseção das duas retas. Veja a Figura\(\PageIndex{3}\).
Determine se o par pedido\((8,5)\) é uma solução para o sistema a seguir.
\[\begin{align*} 5x−4y &= 20 \\ 2x+1 &= 3y \end{align*}\]
- Resposta
-
Não é uma solução.
Resolvendo sistemas de equações por meio de gráficos
Existem vários métodos para resolver sistemas de equações lineares. Para um sistema de equações lineares em duas variáveis, podemos determinar o tipo de sistema e a solução representando graficamente o sistema de equações no mesmo conjunto de eixos.
Resolva o seguinte sistema de equações representando graficamente. Identifique o tipo de sistema.
\[\begin{align*} 2x+y &= −8 \\ x−y &= −1 \end{align*}\]
Solução
Resolva a primeira equação para\(y\).
\[\begin{align*} 2x+y &= −8 \\ y &= −2x−8 \end{align*}\]
Resolva a segunda equação para\(y\).
\[\begin{align*} x−y &= −1 \\ y &= x+1 \end{align*}\]
Faça um gráfico de ambas as equações no mesmo conjunto de eixos da Figura\(\PageIndex{4}\).
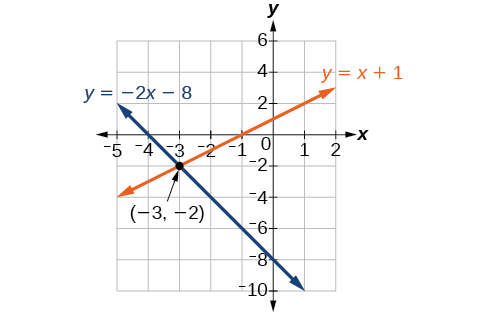
As linhas parecem se cruzar no ponto\((−3,−2)\). Podemos verificar se essa é a solução para o sistema substituindo o par ordenado em ambas as equações.
\[\begin{align*} 2(−3)+(−2) &= −8 \\ −8 &= −8 \text{ True} \\ (−3)−(−2) &= −1 \\ −1 &= −1 \text{ True} \end{align*}\]
A solução para o sistema é o par ordenado\((−3,−2)\), portanto, o sistema é independente.
Resolva o seguinte sistema de equações representando graficamente.
\[\begin{align*} 2x−5y &= −25 \\ −4x+5y &= 35 \end{align*}\]
- Resposta
-
A solução para o sistema é o par pedido\((−5,3)\).
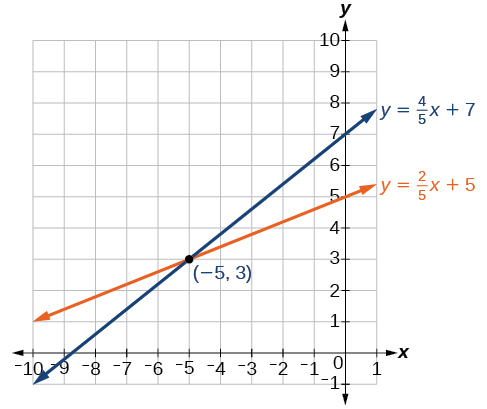
Figura\(\PageIndex{5}\)
A representação gráfica pode ser usada se o sistema for inconsistente ou dependente?
Sim, em ambos os casos, ainda podemos representar graficamente o sistema para determinar o tipo de sistema e a solução. Se as duas linhas estiverem paralelas, o sistema não tem solução e é inconsistente. Se as duas linhas forem idênticas, o sistema tem soluções infinitas e é um sistema dependente.
Resolvendo sistemas de equações por substituição
Resolver um sistema linear em duas variáveis por meio de gráficos funciona bem quando a solução consiste em valores inteiros, mas se nossa solução contiver decimais ou frações, não é o método mais preciso. Vamos considerar mais dois métodos para resolver um sistema de equações lineares que são mais precisas do que a representação gráfica. Um desses métodos é resolver um sistema de equações pelo método de substituição, no qual resolvemos uma das equações para uma variável e, em seguida, substituímos o resultado na segunda equação para resolver a segunda variável. Lembre-se de que podemos resolver apenas uma variável por vez, razão pela qual o método de substituição é valioso e prático.
- Resolva uma das duas equações para uma das variáveis em termos da outra.
- Substitua a expressão dessa variável na segunda equação e resolva a variável restante.
- Substitua essa solução em qualquer uma das equações originais para encontrar o valor da primeira variável. Se possível, escreva a solução como um par ordenado.
- Verifique a solução nas duas equações.
Resolva o seguinte sistema de equações por substituição.
\[\begin{align*} −x+y &= −5 \\ 2x−5y &= 1 \end{align*}\]
Solução
Primeiro, resolveremos a primeira equação para\(y\).
\[\begin{align*} −x+y &=−5 \\ y &= x−5 \end{align*}\]
Agora podemos substituir a expressão\(x−5\) por\(y\) na segunda equação.
\[\begin{align*} 2x−5y &= 1 \\ 2x−5(x−5) &= 1 \\ 2x−5x+25 &= 1 \\ −3x &= −24 \\ x &= 8 \end{align*}\]
Agora, substituímos\(x=8\) a primeira equação e resolvemos por\(y\).
\[\begin{align*} −(8)+y &= −5 \\ y &= 3 \end{align*}\]
Nossa solução é\((8,3)\).
Verifique a solução substituindo-a\((8,3)\) nas duas equações.
\[\begin{align*} −x+y &= −5 \\ −(8)+(3) &= −5 \text{ True} \\ 2x−5y &= 1 \\ 2(8)−5(3) &= 1 \text{ True} \end{align*}\]
Resolva o seguinte sistema de equações por substituição.
\[\begin{align*} x &= y+3 \\ 4 &= 3x−2y \end{align*}\]
- Resposta
-
\((−2,−5)\)
O método de substituição pode ser usado para resolver qualquer sistema linear em duas variáveis?
Sim, mas o método funciona melhor se uma das equações contiver um coeficiente de\(1\) ou mais\(–1\) que não precisemos lidar com frações.
Resolvendo sistemas de equações em duas variáveis pelo método de adição
Um terceiro método para resolver sistemas de equações lineares é o método de adição. Nesse método, adicionamos dois termos com a mesma variável, mas com coeficientes opostos, para que a soma seja zero. Obviamente, nem todos os sistemas são configurados com os dois termos de uma variável com coeficientes opostos. Freqüentemente, devemos ajustar uma ou ambas as equações por multiplicação para que uma variável seja eliminada por adição.
- Escreva as duas equações com variáveis x e y no lado esquerdo do sinal de igual e constantes no lado direito.
- Escreva uma equação acima da outra, alinhando as variáveis correspondentes. Se uma das variáveis na equação superior tiver o coeficiente oposto da mesma variável na equação inferior, adicione as equações, eliminando uma variável. Caso contrário, use a multiplicação por um número diferente de zero para que uma das variáveis na equação superior tenha o coeficiente oposto da mesma variável na equação inferior e, em seguida, adicione as equações para eliminar a variável.
- Resolva a equação resultante para a variável restante.
- Substitua esse valor em uma das equações originais e resolva a segunda variável.
- Verifique a solução substituindo os valores na outra equação.
Resolva o sistema de equações fornecido por adição.
\[\begin{align*} x+2y &= −1 \\ −x+y &=3 \end{align*}\]
Solução
Ambas as equações já estão definidas como iguais a uma constante. Observe que o coeficiente de\(x\) na segunda equação,\(–1\), é o oposto do coeficiente de\(x\) na primeira equação,\(1\). Podemos adicionar as duas equações para eliminar\(x\) sem precisar multiplicar por uma constante.
\[\begin{align*} x+2y &= -1 \\ \underline{-x+y}& = \underline{3} \\ 3y&= 2 \\ \end{align*}\]
Agora que eliminamos\(x\), podemos resolver a equação resultante para\(y\).
\[\begin{align*} 3y &= 2 \\ y &=\dfrac{2}{3} \end{align*}\]
Em seguida, substituímos esse valor\(y\) em uma das equações originais e resolvemos\(x\).
\[\begin{align*} −x+y &= 3 \\ −x+\dfrac{2}{3} &= 3 \\ −x &= 3−\dfrac{2}{3} \\ −x &= \dfrac{7}{3} \\ x &= −\dfrac{7}{3} \end{align*}\]
A solução para esse sistema é\(\left(−\dfrac{7}{3},\dfrac{2}{3}\right)\).
Verifique a solução na primeira equação.
\[\begin{align*} x+2y &= −1 \\ \left(−\dfrac{7}{3}\right)+2\left(\dfrac{2}{3}\right) &= \\ −\dfrac{7}{3}+\dfrac{4}{3} &= −\dfrac{3}{3} \\ −1 &= −1 \;\;\;\;\;\;\;\; \text{True} \end{align*}\]
Análise
Obtemos uma perspectiva importante sobre sistemas de equações observando a representação gráfica. Veja\(\PageIndex{6}\) a Figura para descobrir que as equações se cruzam na solução. Não precisamos perguntar se pode haver uma segunda solução porque observar o gráfico confirma que o sistema tem exatamente uma solução.
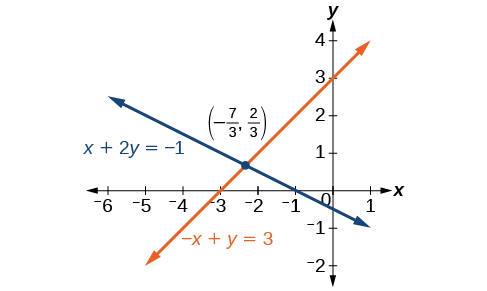
Resolva o sistema de equações fornecido pelo método de adição.
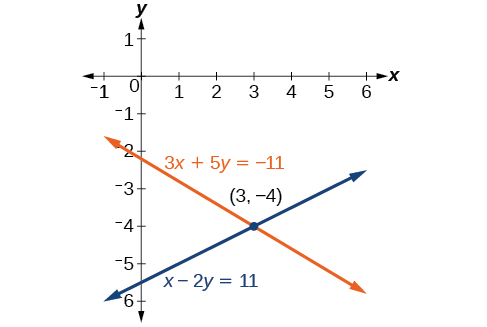
\[\begin{align*} 3x+5y &= −11 \\ x−2y &= 11 \end{align*}\]
Solução
Adicionar essas equações conforme apresentadas não eliminará uma variável. No entanto, vemos que a primeira equação tem\(3x\) nela e a segunda equação tem\(x\). Então, se multiplicarmos a segunda equação por\(−3\), os termos x serão adicionados a zero.
\[\begin{align*} x−2y &= 11 \\ −3(x−2y) &=−3(11) \;\;\;\;\;\;\;\; \text{Multiply both sides by }−3. \\ −3x+6y &= −33 \;\;\;\;\;\;\;\;\; \text{Use the distributive property.} \end{align*}\]
Agora, vamos adicioná-los.
\[\begin{align*} 3x+5y &= -11 \\ \underline{-3x+6y }& = \underline{-33} \\ 11y&= -44 \\ y&= -4 \end{align*}\]
Na última etapa,\(y=−4\) substituímos por uma das equações originais e resolvemos\(x\).
\[\begin{align*} 3x+5y &= −11 \\ 3x+5(−4) &= −11 \\ 3x−20 &= −11 \\ 3x &= 9 \\ x &= 3 \end{align*}\]
Nossa solução é o par encomendado\((3,−4)\). Veja a Figura\(\PageIndex{7}\). Verifique a solução na segunda equação original.
\[\begin{align*} x−2y &= 11 \\ (3)−2(−4) &= 3+8 \\ &= 11 \;\;\;\;\;\;\;\;\;\; \text{True} \end{align*}\]
Resolva o sistema de equações por adição.
\[\begin{align*} 2x−7y &= 2 \\ 3x+y &= −20 \end{align*}\]
- Resposta
-
\((−6,−2)\)
Resolva o sistema de equações fornecido em duas variáveis por adição.
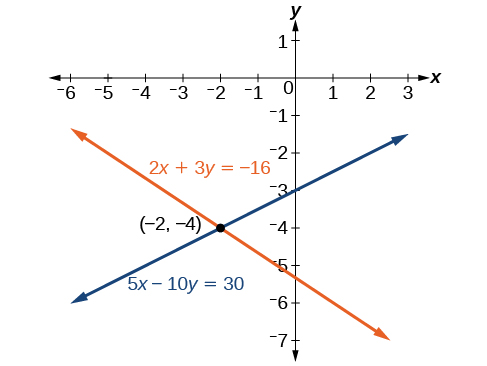
\[\begin{align*} 2x+3y &= −16 \\ 5x−10y &= 30 \end{align*}\]
Solução
Uma equação tem\(2x\) e a outra tem\(5x\). O mínimo múltiplo comum é\(10x\), portanto, teremos que multiplicar as duas equações por uma constante para eliminar uma variável. Vamos eliminar\(x\) multiplicando a primeira equação por\(−5\) e a segunda equação por\(2\).
\[\begin{align*} −5(2x+3y) &= −5(−16) \\ −10x−15y &= 80 \\ 2(5x−10y) &= 2(30) \\ 10x−20y &= 60 \end{align*}\]
Em seguida, adicionamos as duas equações.
\[\begin{align*} -10x-15y &= 80 \\ \underline{10x-20y}& = \underline{60} \\ -35y&= 140 \\ y&= -4 \end{align*}\]
Substitua\(y=−4\) na primeira equação original.
\[ \begin{align*} 2x+3(−4) &=−16 \\ 2x−12 &= −16 \\ 2x &= −4 \\ x &=−2 \end{align*}\]
A solução é\((−2,−4)\). Verifique isso na outra equação.
\[\begin{align*} 5x−10y &= 30 \\ 5(−2)−10(−4) &= 30 \\ −10+40 &= 30 \\30 &=30 \end{align*}\]
Veja a Figura\(\PageIndex{8}\).
Resolva o sistema de equações fornecido em duas variáveis por adição.
\[ \begin{align*} \dfrac{x}{3}+\dfrac{y}{6} &= 3 \\ \dfrac{x}{2}−\dfrac{y}{4} &= 1 \end{align*}\]
Solução
Primeiro, limpe cada equação de frações multiplicando os dois lados da equação pelo denominador menos comum.
\[\begin{align*} 6\left(\dfrac{x}{3}+\dfrac{y}{6}\right) &= 6(3) \\ 2x+y &= 18 \\ 4\left(\dfrac{x}{2}−\dfrac{y}{4}\right) &= 4(1) \\ 2x−y &= 4 \end{align*}\]
Agora multiplique a segunda equação por\(−1\) para que possamos eliminar a variável x.
\[\begin{align*} −1(2x−y) &= −1(4) \\ −2x+y &= −4 \end{align*}\]
Adicione as duas equações para eliminar a\(x\) variável -e resolver a equação resultante.
\[\begin{align*} 2x+y &= 18 \\ −2x+y &= −4 \\ 2y &= 14 \\ y &=7 \end{align*}\]
Substitua\(y=7\) na primeira equação.
\[\begin{align*} 2x+(7) &= 18 \\ 2x &= 11 \\ x &= \dfrac{11}{2} \\ &= 7.5 \end{align*}\]
A solução é\(\left(\dfrac{11}{2},7\right)\). Verifique isso na outra equação.
\[\begin{align*} \dfrac{x}{2}−\dfrac{y}{4} &= 1 \\ \dfrac{\dfrac{11}{2}}{2}−\dfrac{7}{4} &=1 \\ \dfrac{11}{4}−\dfrac{7}{4} &=1 \\ \dfrac{4}{4} &=1 \end{align*}\]
Resolva o sistema de equações por adição.
\[\begin{align*} 2x+3y &= 8 \\ 3x+5y &= 10 \end{align*}\]
- Resposta
-
\((10,−4)\)
Identificação de sistemas inconsistentes de equações contendo duas variáveis
Agora que temos vários métodos para resolver sistemas de equações, podemos usar os métodos para identificar sistemas inconsistentes. Lembre-se de que um sistema inconsistente consiste em linhas paralelas que têm a mesma inclinação, mas diferentes interceptações y. Eles nunca se cruzarão. Ao procurar uma solução para um sistema inconsistente, apresentaremos uma declaração falsa, como\(12=0\).
Resolva o seguinte sistema de equações.
\[\begin{align*} x &= 9−2y \\ x+2y &= 13 \end{align*}\]
Solução
Podemos abordar esse problema de duas maneiras. Como uma equação já foi resolvida\(x\), a etapa mais óbvia é usar a substituição.
\[\begin{align*} x+2y &= 13 \\ (9−2y)+2y &= 13 \\ 9+0y &= 13 \\ 9 &= 13 \end{align*}\]
Claramente, essa afirmação é uma contradição porque\(9≠13\). Portanto, o sistema não tem solução.
A segunda abordagem seria primeiro manipular as equações para que ambas estivessem na forma de interceptação de inclinação. Manipulamos a primeira equação da seguinte forma.
\[\begin{align*} x &= 9−2y \\ 2y &= −x+9 \\ y &= −\dfrac{1}{2}x+\dfrac{9}{2} \end{align*}\]
Em seguida, convertemos a segunda equação expressa na forma de interceptação de inclinação.
\[\begin{align*} x+2y &= 13 \\ 2y &= −x+13 \\ y &= −\dfrac{1}{2}x+\dfrac{13}{2} \end{align*}\]
Comparando as equações, vemos que elas têm a mesma inclinação, mas\(y\) interceptações diferentes. Portanto, as linhas são paralelas e não se cruzam.
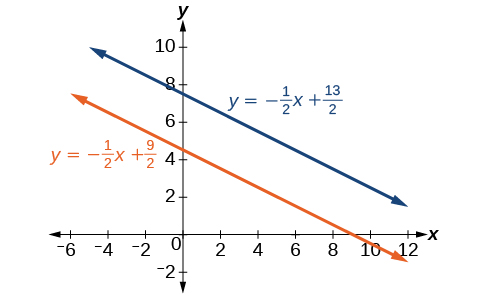
\[\begin{align*} y &= −\dfrac{1}{2}x+\dfrac{9}{2} \\ y &= −\dfrac{1}{2}x+\dfrac{13}{2} \end{align*}\]
Análise
Escrever as equações na forma de interceptação de inclinação confirma que o sistema é inconsistente porque todas as linhas se cruzarão eventualmente, a menos que sejam paralelas. As linhas paralelas nunca se cruzarão; portanto, as duas linhas não têm pontos em comum. Os gráficos das equações neste exemplo são mostrados na Figura\(\PageIndex{9}\).
Resolva o seguinte sistema de equações em duas variáveis.
\[\begin{align*} 2y−2x &= 2 \\ 2y−2x &= 6 \end{align*}\]
- Resposta
-
Sem solução. É um sistema inconsistente.
Expressando a solução de um sistema de equações dependentes contendo duas variáveis
Lembre-se de que um sistema dependente de equações em duas variáveis é um sistema no qual as duas equações representam a mesma linha. Os sistemas dependentes têm um número infinito de soluções porque todos os pontos em uma linha também estão na outra linha. Depois de usar a substituição ou adição, a equação resultante será uma identidade, como\(0=0\).
Encontre uma solução para o sistema de equações usando o método de adição.
\[\begin{align*} x+3y &= 2 \\ 3x+9y &= 6 \end{align*}\]
Solução
Com o método de adição, queremos eliminar uma das variáveis adicionando as equações. Nesse caso, vamos nos concentrar em eliminar\(x\). Se multiplicarmos os dois lados da primeira equação por\(−3\), poderemos eliminar a variável x.
\[\begin{align*} x+3y &= 2 \\ (−3)(x+3y) &= (−3)(2) \\ −3x−9y &= −6 \end{align*}\]
Agora, adicione as equações.
\[\begin{align*} -3x-9y &= -6 \\ \underline{+\space 3x+9y}& = \underline{6} \\ 0&= 0 \\ \end{align*}\]
Podemos ver que haverá um número infinito de soluções que satisfazem as duas equações.
Análise
Se reescrevermos as duas equações na forma de interceptação de inclinação, talvez saibamos como seria a solução antes de adicionar. Vamos ver o que acontece quando convertemos o sistema na forma de interceptação de inclinação.
\[ \begin{align*} x+3y &= 2 \\ 3y &= −x+2 \\ y &= −\dfrac{1}{3}x+\dfrac{2}{3} \\ 3x+9y &= 6 \\ 9y &=−3x+6 \\ y &= −\dfrac{3}{9}x+\dfrac{6}{9} \\ y &= −\dfrac{1}{3}x+\dfrac{2}{3} \end{align*}\]
Veja a Figura\(\PageIndex{10}\). Observe que os resultados são os mesmos. A solução geral para o sistema é\(\left(x, −\dfrac{1}{3}x+\dfrac{2}{3}\right)\).
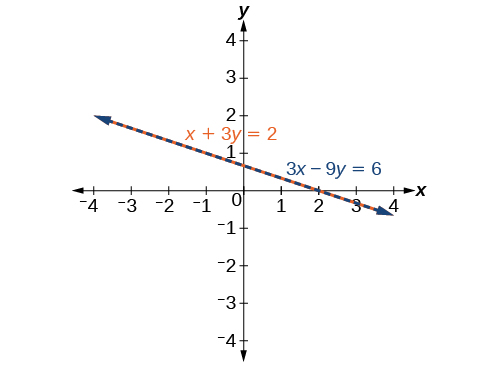
Resolva o seguinte sistema de equações em duas variáveis.
\[\begin{align*} y−2x &= 5 \\ −3y+6x &= −15 \end{align*}\]
- Resposta
-
O sistema é dependente, então existem soluções infinitas do formulário\((x,2x+5)\).
Usando sistemas de equações para investigar lucros
Usando o que aprendemos sobre sistemas de equações, podemos retornar ao problema de fabricação do skate no início da seção. A função de receita do fabricante do skate é a função usada para calcular a quantidade de dinheiro que entra no negócio. Ela pode ser representada pela equação\(R=xp\), onde\(x\) = quantidade e\(p\) = preço. A função de receita é mostrada em laranja na Figura\(\PageIndex{11}\).
A função de custo é a função usada para calcular os custos de fazer negócios. Inclui custos fixos, como aluguel e salários, e custos variáveis, como serviços públicos. A função de custo é mostrada em azul na Figura\(\PageIndex{11}\). O\(x\) eixo -representa a quantidade em centenas de unidades. O\(y\) eixo -representa custo ou receita em centenas de dólares.
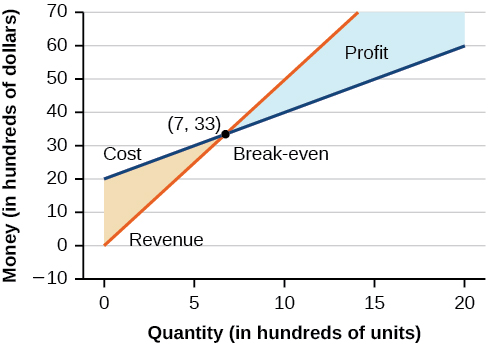
O ponto no qual as duas linhas se cruzam é chamado de ponto de equilíbrio. Podemos ver no gráfico que, se\(700\) as unidades são produzidas, o custo é\($3,300\) e a receita também\($3,300\). Em outras palavras, a empresa quebra mesmo que produza e venda\(700\) unidades. Eles não ganham dinheiro nem perdem dinheiro.
A região sombreada à direita do ponto de equilíbrio representa quantidades com as quais a empresa obtém lucro. A região sombreada à esquerda representa quantidades pelas quais a empresa sofre uma perda. A função de lucro é a função de receita menos a função de custo, escrita como\(P(x)=R(x)−C(x)\). Claramente, saber a quantidade pela qual o custo é igual à receita é de grande importância para as empresas.
Dada a função de custo\(C(x)=0.85x+35,000\) e a função de receita\(R(x)=1.55x\), encontre o ponto de equilíbrio e a função de lucro.
Solução
Escreva o sistema de equações usando\(y\) para substituir a notação da função.
\[\begin{align*} y &= 0.85x+35,000 \\ y &= 1.55x \end{align*}\]
Substitua a expressão\(0.85x+35,000\) da primeira equação pela segunda equação e resolva\(x\).
\[\begin{align*} 0.85x+35,000 &= 1.55x \\ 35,000 &= 0.7x \\ 50,000 &= x \end{align*}\]
Em seguida, substituímos\(x=50,000\) a função de custo ou a função de receita.
\(1.55(50,000)=77,500\)
O ponto de equilíbrio é\((50,000,77,500)\).
A função de lucro é encontrada usando a fórmula\(P(x)=R(x)−C(x)\).
\[\begin{align*} P(x) &= 1.55x−(0.85x+35,000) \\ &=0.7x−35,000 \end{align*}\]
A função de lucro é\(P(x)=0.7x−35,000\).
Análise
O custo de produção de\(50,000\) unidades é\($77,500\), e a receita da venda de\(50,000\) unidades também é\($77,500\). Para obter lucro, a empresa deve produzir e vender mais do que\(50,000\) unidades. Veja a Figura\(\PageIndex{12}\).
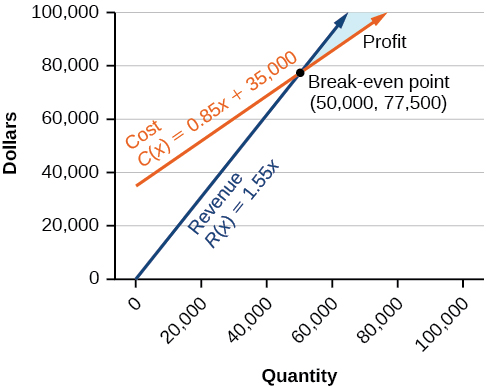
Vemos no gráfico da Figura\(\PageIndex{13}\) que a função de lucro tem um valor negativo até\(x=50,000\), quando o gráfico cruza o\(x\) eixo. Em seguida, o gráfico emerge em\(y\) valores positivos e continua nesse caminho, pois a função de lucro é uma linha reta. Isso ilustra que o ponto de equilíbrio para as empresas ocorre quando a função de lucro é\(0\). A área à esquerda do ponto de equilíbrio representa operar com prejuízo.
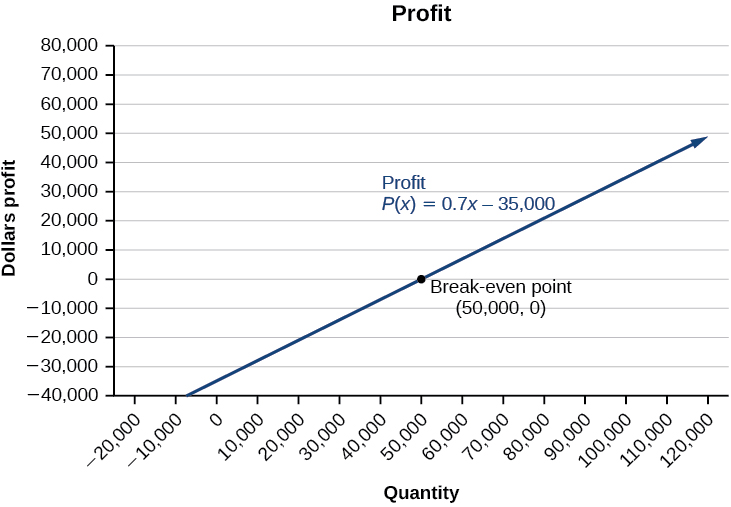
O custo de um ingresso para o circo é\($25.00\) para crianças e\($50.00\) adultos. Em um determinado dia, a frequência ao circo é\(2,000\) e a receita total do portão é\($70,000\). Quantas crianças e quantos adultos compraram ingressos?
Solução
Seja\(c\) = o número de crianças e\(a\) = o número de adultos presentes.
O número total de pessoas é\(2,000\). Podemos usar isso para escrever uma equação para o número de pessoas no circo naquele dia.
\(c+a=2,000\)
A receita de todas as crianças pode ser obtida multiplicando-se\($25.00\) pelo número de filhos,\(25c\). A receita de todos os adultos pode ser obtida multiplicando-se\($50.00\) pelo número de adultos,\(50a\). A receita total é\($70,000\). Podemos usar isso para escrever uma equação para a receita.
\(25c+50a=70,000\)
Agora temos um sistema de equações lineares em duas variáveis.
\(c+a=2,000\)
\(25c+50a=70,000\)
Na primeira equação, o coeficiente de ambas as variáveis é\(1\). Podemos resolver rapidamente a primeira equação para qualquer um\(c\) ou\(a\). Nós resolveremos por\(a\).
\[\begin{align*} c+a &= 2,000 \\ a &= 2,000−c \end{align*}\]
Substitua a expressão\(2,000−c\) na segunda equação por a e resolva por\(c\).
\[\begin{align*} 25c+50(2,000−c) &= 70,000 \\ 25c+100,000−50c &= 70,000 \\ −25c &= −30,000 \\ c &= 1,200 \end{align*}\]
Substitua\(c=1,200\) na primeira equação a ser resolvida\(a\).
\[\begin{align*} 1,200+a &= 2,000 \\ a &= 800 \end{align*}\]
Descobrimos que\(1,200\) crianças e\(800\) adultos compraram ingressos para o circo naquele dia.
Os vales-refeição no circo custam\($4.00\) para crianças e\($12.00\) adultos. Se\(1,650\) vales-refeição foram comprados para um total de\($14,200\),, quantas crianças e quantos adultos compraram vales-refeição?
- Resposta
-
\(700\)crianças,\(950\) adultos
Acesse esses recursos on-line para obter instruções e práticas adicionais com sistemas de equações lineares.
Conceitos-chave
- Um sistema de equações lineares consiste em duas ou mais equações compostas por duas ou mais variáveis, de forma que todas as equações no sistema sejam consideradas simultaneamente.
- A solução para um sistema de equações lineares em duas variáveis é qualquer par ordenado que satisfaça cada equação de forma independente. Veja o exemplo\(\PageIndex{1}\).
- Os sistemas de equações são classificados como independentes com uma solução, dependentes de um número infinito de soluções ou inconsistentes com nenhuma solução.
- Um método para resolver um sistema de equações lineares em duas variáveis é por meio de gráficos. Neste método, representamos graficamente as equações no mesmo conjunto de eixos. Veja o exemplo\(\PageIndex{2}\).
- Outro método para resolver um sistema de equações lineares é por substituição. Nesse método, resolvemos uma variável em uma equação e substituímos o resultado na segunda equação. Veja o exemplo\(\PageIndex{3}\).
- Um terceiro método para resolver um sistema de equações lineares é por adição, no qual podemos eliminar uma variável adicionando coeficientes opostos às variáveis correspondentes. Veja o exemplo\(\PageIndex{4}\).
- Muitas vezes, é necessário multiplicar uma ou ambas as equações por uma constante para facilitar a eliminação de uma variável ao somar as duas equações. Veja exemplo\(\PageIndex{5}\)\(\PageIndex{6}\), exemplo e exemplo\(\PageIndex{7}\).
- Qualquer um dos métodos de resolver um sistema de equações resulta em uma afirmação falsa para sistemas inconsistentes porque eles são feitos de linhas paralelas que nunca se cruzam. Veja o exemplo\(\PageIndex{8}\).
- A solução para um sistema de equações dependentes sempre será verdadeira porque ambas as equações descrevem a mesma linha. Veja o exemplo\(\PageIndex{9}\).
- Sistemas de equações podem ser usados para resolver problemas do mundo real que envolvem mais de uma variável, como aqueles relacionados à receita, custo e lucro. Veja o exemplo\(\PageIndex{10}\) e o exemplo\(\PageIndex{11}\).


