7.6: Modelagem com equações trigonométricas
- Page ID
- 189339
Suponha que traçamos as temperaturas médias diárias na cidade de Nova York ao longo de um ano. Esperamos encontrar as temperaturas mais baixas em janeiro e fevereiro e as mais altas em julho e agosto. Esse ciclo familiar se repete ano após ano e, se fôssemos estender o gráfico por vários anos, ele se pareceria com uma função periódica.

Muitos outros fenômenos naturais também são periódicos. Por exemplo, as fases da lua têm um período de aproximadamente 28 dias, e os pássaros sabem voar para o sul quase na mesma época todos os anos. Então, como podemos modelar uma equação para refletir o comportamento periódico? Primeiro, devemos coletar e registrar dados. Em seguida, encontramos uma função que se assemelha a um padrão observado. Finalmente, fazemos as alterações necessárias na função para obter um modelo confiável. Nesta seção, examinaremos mais detalhadamente tipos específicos de comportamento periódico e equações de modelo para ajustar os dados.
Determinando a amplitude e o período de uma função senoidal
Qualquer movimento que se repete em um período de tempo fixo é considerado movimento periódico e pode ser modelado por uma função senoidal. A amplitude de uma função senoidal é a distância da linha média até o valor máximo, ou da linha média até o valor mínimo. A linha média é o valor médio. As funções sinusoidais oscilam acima e abaixo da linha média, são periódicas e repetem valores em ciclos definidos. Recorde, a partir dos gráficos das funções seno e cosseno, que o período da função seno e da função cosseno é\(2π\). Em outras palavras, para qualquer valor de\(x\),
\[ \sin(x±2πk)=\sin x \; \text{and} \; \cos(x±2πk)=\cos x \]
onde\(k\) é um número inteiro.
FORMA PADRÃO DE EQUAÇÕES SENOIDAIS
As formas gerais de uma equação senoidal são dadas como
\[y=A \sin(Bt−C)+D\]
ou
\[ y=A \cos(Bt−C)+D\]
onde\(\text{amplitude}=|A|,B\) está relacionado ao período de tal forma que\(\text{period}=\frac{2π}{B},C\) é a mudança de fase tal que\(\frac{C}{B}\) denota o deslocamento horizontal e\(D\) representa a mudança vertical do gráfico principal do gráfico.
Observe que os modelos às vezes são escritos como
\[y=a \sin (ω t±C)+D\]
ou
\[y=a \cos(ω t±C)+D,\]
com um período que é dado como\(\frac{2π}{ω}\).
A diferença entre os gráficos do seno e do cosseno é que o gráfico do seno começa com o valor médio da função e o gráfico do cosseno começa com o valor máximo ou mínimo da função.
Exemplo\(\PageIndex{1}\): Showing How the Properties of a Trigonometric Function Can Transform a Graph
Mostre a transformação do gráfico de\(y=\sin x\) em gráfico de\(y=2 \sin(4x−\frac{π}{2})+2\).
Solução
Considere a série de gráficos na Figura\(\PageIndex{1}\) e a forma como cada alteração na equação altera a imagem.
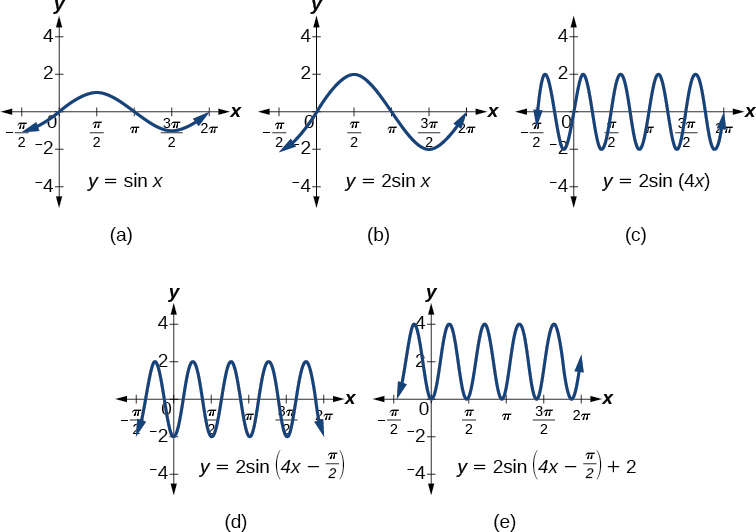
- O gráfico básico de\(y=\sin x\)
- Alterar a amplitude de 1 para 2 gera o gráfico de\(y=2 \sin x\).
- O período da função seno muda com o valor de\(B,\) tal que\(\text{period}=\frac{2π}{B}.\) Aqui temos,\(B=4,\) o que se traduz em um período de\(\frac{π}{2}\). O gráfico completa um ciclo completo em\(\frac{π}{2}\) unidades.
- O gráfico exibe um deslocamento horizontal igual a\(\frac{C}{B}\), ou\(\frac{\frac{π}{2}}{4}=\frac{π}{8}\).
- Finalmente, o gráfico é deslocado verticalmente pelo valor de\(D\). Nesse caso, o gráfico é deslocado para cima em 2 unidades.
Exemplo\(\PageIndex{2}\): Finding the Amplitude and Period of a Function
Encontre a amplitude e o período das seguintes funções e represente graficamente um ciclo.
- \(y=2 \sin (\frac{1}{4}x)\)
- \(y=−3 \sin (2x+\frac{π}{2})\)
- \(y= \cos x+3\)
Solução
Resolveremos esses problemas de acordo com os modelos.
- \(y=2 \sin (\frac{1}{4}x)\)envolve seno, então usamos a forma\[y=A \sin (Bt+C)+D \nonumber\] Sabemos que\(| A |\) é a amplitude, então a amplitude é 2. O período é\(\frac{2π}{B}\) assim que o período é\[\begin{align*} \dfrac{2π}{B} &=\dfrac{2π}{\frac{1}{4}} \\ & =8π \end{align*}\] Veja o gráfico na Figura\(\PageIndex{3}\).
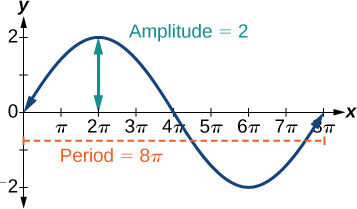
- \(y=−3 \sin(2x+ \frac{π}{2})\)envolve seno, então usamos a forma\[y=A \sin (Bt−C)+D \nonumber\] Amplitude é\(| A |\), então a amplitude é\(|−3|=3.\) Como\(A\) é negativa, o gráfico é refletido sobre o eixo x. O período é\(\frac{2π}{B}\), então o período é\[\dfrac{2π}{B}=\dfrac{2π}{2}=π \nonumber\] O gráfico é deslocado para a esquerda em\(\frac{C}{B}=\frac{\frac{π}{2}}{2}=\frac{π}{4}\) unidades. Veja a Figura\(\PageIndex{4}\).
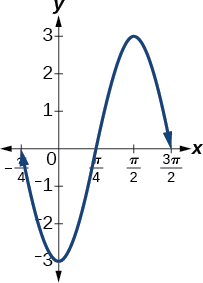
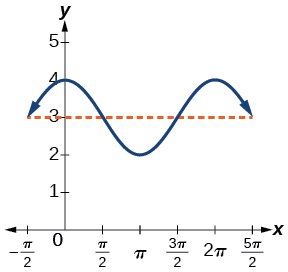
- \(y= \cos x+3\)envolve cosseno, então usamos a forma
- \[y=A \cos (Bt±C)+D \nonumber\]A amplitude é\(| A |\), então a amplitude é 1 e o período é\(2π\) (Figura\(\PageIndex{5}\). Esta é a função de cosseno padrão deslocada para três unidades.
Exercício\(\PageIndex{1}\):
Quais são a amplitude e o período da função\(y=3 \cos (3πx)\)?
- Responda
-
A amplitude é\(3,\) e o período é\(\frac{2}{3}\).
Encontrando equações e representando graficamente funções senoidais
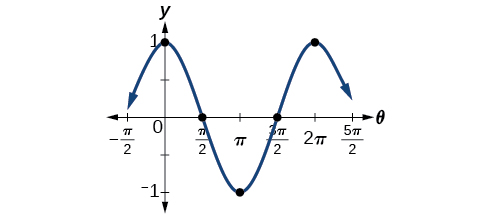
Um método de representação gráfica de funções senoidais é encontrar cinco pontos-chave. Esses pontos corresponderão a intervalos de igual comprimento representando\(\frac{1}{4}\) o período. Os pontos-chave indicarão a localização dos valores máximo e mínimo. Se não houver mudança vertical, eles também indicarão interceptações x. Por exemplo, suponha que desejemos representar graficamente a função.\(y=cos θ.\) Sabemos que o período é\(2π\), então encontramos o intervalo entre os pontos-chave da seguinte forma.
\[\frac{2π}{4}=\frac{π}{2} \nonumber\]
Começando com,\(θ=0,\) calculamos o primeiro valor y, adicionamos a duração do intervalo\(\frac{π}{2}\) e calculamos o segundo valor y.\(0\) Em seguida, adicionamos\(\frac{π}{2}\) repetidamente até que os cinco pontos-chave sejam determinados. O último valor deve ser igual ao primeiro, pois os cálculos abrangem um período completo. Fazendo uma tabela semelhante à Tabela\(\PageIndex{1}\), podemos ver esses pontos-chave claramente no gráfico mostrado na Figura\(\PageIndex{6}\).
| \(θ\) | \(0\) | \(\frac{π}{2}\) | \(π\) | \(\frac{3π}{2}\) | \(2π\) |
|---|---|---|---|---|---|
| \(y=\cos θ\) | \(1\) | \(0\) | −1−1 | \(0\) | \(1\) |
Exemplo\(\PageIndex{3}\): Graphing Sinusoidal Functions Using Key Points
Faça um gráfico da função\(y=−4 \cos (πx)\) usando amplitude, período e pontos-chave.
Solução
A amplitude é\(|−4|=4.\) O período é\(\frac{2π}{ω}=\frac{2π}{π}=2.\) (Lembre-se de que às vezes nos referimos\(B\) como\(ω.\)) Um ciclo do gráfico pode ser desenhado ao longo do intervalo\([ 0,2 ]\). Para encontrar os pontos-chave, dividimos o período por 4. Faça uma tabela semelhante à Figura\(\PageIndex{1}\):, começando com\(x=0\) e depois adicionando\(\frac{1}{2}\) sucessivamente\(x\) e calculando\(y.\) Veja o gráfico na Figura\(\PageIndex{7}\).
| \(x\) | \(0\) | \(\frac{1}{2}\) | \(1\) | \(\frac{3}{2}\) | \(2\) |
|---|---|---|---|---|---|
| \(y=−4 \cos(πx)\) | \(−4\) | \(0\) | \(4\) | \(0\) | \(−4\) |

Exercício\(\PageIndex{2}\):
Faça um gráfico da função\(y=3 \sin(3x)\) usando a amplitude, o período e os cinco pontos-chave.
| \(x\) | 0 | \(\frac{π}{6}\) | \(\frac{π}{3}\) | \(\frac{π}{2}\) | \(\frac{2π}{3}\) |
|---|---|---|---|---|---|
| \(3 \sin (3x)\) | 0 | 3 | 0 | -3 | 0 |
- Responda
-
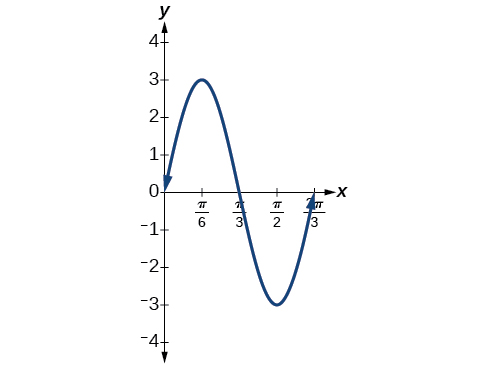
Figura\(\PageIndex{8}\)
Modelando o comportamento periódico
Agora, aplicaremos essas ideias a problemas que envolvem comportamento periódico.
Exemplo\(\PageIndex{4}\): Modeling an Equation and Sketching a Sinusoidal Graph to Fit Criteria
As temperaturas médias mensais de uma pequena cidade no Oregon são apresentadas na tabela\(\PageIndex{1}\). Encontre uma função senoidal da forma\(y=A \sin (Bt−C)+D\) que se ajuste aos dados (arredonde para o décimo mais próximo) e desenhe o gráfico.
| Mês | Temperatura,\(^oF\) |
|---|---|
| janeiro | \ (^Of\) ">42,5 |
| fevereiro | \ (^Of\) ">44,5 |
| Março | \ (^Of\) ">48,5 |
| abril | \ (^Of\) ">52,5 |
| Pode | \ (^Of\) ">58 |
| Junho | \ (^Of\) ">63 |
| Julho | \ (^Of\) ">68,5 |
| agosto | \ (^Of\) ">69 |
| setembro | \ (^Of\) ">64,5 |
| Outubro | \ (^Of\) ">55,5 |
| novembro | \ (^Of\) ">46,5 |
| dezembro | \ (^Of\) ">43,5 |
Solução
Lembre-se de que a amplitude é encontrada usando a fórmula
\[A=\dfrac{\text{largest value −smallest value}}{2}\]
Assim, a amplitude é
\[\begin{align*} |A| & = \dfrac{69−42.5}{2} \\ &=13.25 \end{align*}\]
Os dados abrangem um período de 12 meses,\(\frac{2π}{B}=12\) o que dá\(B=\frac{2π}{12}=\frac{π}{6}\).
O deslocamento vertical é encontrado usando a seguinte equação.
\[D=\dfrac{\text{highest value+lowest value}}{2}\]
Assim, a mudança vertical é\[\begin{align*} D &= \dfrac{69+42.5}{2} &=55.8 \end{align*}\]
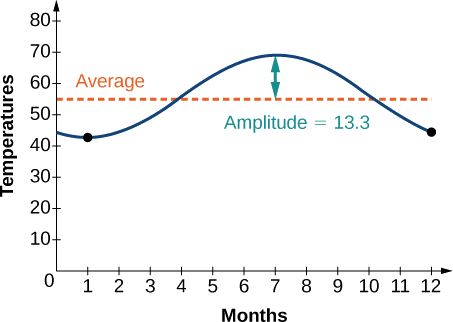
Até agora, temos a equação\(y=13.3 \sin (\frac{π}{6}x−C)+55.8\).
Para encontrar a mudança horizontal, inserimos\(y\) os valores\(x\) e para o primeiro mês e resolvemos para\(C\).
\[\begin{align*} 42.5 & =13.3 \sin (\frac{π}{6}(1)−C)+55.8 \\ −13.3 & =13.3 \sin (\frac{π}{6}−C) \\ −1 & =\sin (\frac{π}{6}−C) \;\;\;\;\;\;\;\; \sin θ=−1→ θ=−\frac{π}{2} \\ \frac{π}{6}−C=−\frac{π}{2} \\ \frac{π}{6}+\frac{π}{2} & =C \\ &=\frac{2π}{3} \end{align*}\]
Nós temos a equação\(y=13.3 \sin (\frac{π}{6}x−\frac{2π}{3})+55.8\). Veja o gráfico na Figura\(\PageIndex{9}\).
Exemplo\(\PageIndex{5}\): Describing Periodic Motion
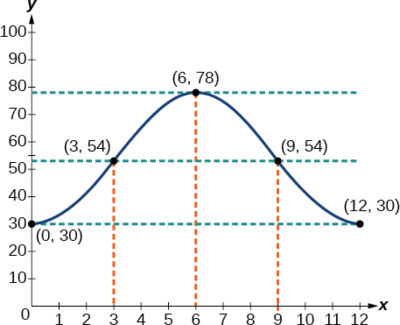
O ponteiro das horas do grande relógio na parede da Union Station mede 24 polegadas de comprimento. Ao meio-dia, a ponta do ponteiro das horas está a 30 polegadas do teto. Às 15h, a ponta está a 54 polegadas do teto e às 18h, a 78 polegadas. Às 21h, ele está novamente a 54 polegadas do teto e, à meia-noite, a ponta do ponteiro das horas retorna à sua posição original a 30 polegadas do teto. Deixe\(y\) igualar a distância da ponta do ponteiro das horas até o teto\(x\) horas após o meio dia. Encontre a equação que modela o movimento do relógio e desenhe o gráfico.
Solução
Comece criando uma tabela de valores conforme mostrado na Tabela\(\PageIndex{3}\).
| \(x\) | \(y\) | Pontos a serem traçados |
|---|---|---|
| \ (x\) ">Meio dia | \ (y\) ">30 em | \((0,30)\) |
| \ (x\) ">3 PM | \ (y\) ">54 em | \((3,54)\) |
| \ (x\) ">6 PM | \ (y\) ">78 em | \((6,78)\) |
| \ (x\) ">9 PM | \ (y\) ">54 em | \((9,54)\) |
| \ (x\) ">Meia-noite | \ (y\) ">30 em | \((12,30)\) |
Para modelar uma equação, primeiro precisamos encontrar a amplitude.
\[\begin{align*} | A | & =| \dfrac{78−30}{2} | \\ &=24 \end{align*}\]
O ciclo do relógio se repete a cada 12 horas. Assim,
\[\begin{align*} B &=\dfrac{2π}{12} \\ &= \dfrac{π}{6} \end{align*}\]
A mudança vertical é
\[\begin{align*} D & = \dfrac{78+30}{2} \\ &=54 \end{align*}\]
Não há deslocamento horizontal, então,\(C=0.\) como a função começa com o valor mínimo de\(y\) quando\(x=0\) (em oposição ao valor máximo), usaremos a função cosseno com o valor negativo para\(A\). Na forma,\(y=A \cos (Bx±C)+D,\) a equação é
\[y=−24 \cos (\dfrac{π}{6}x)+54\]
Veja a Figura\(\PageIndex{10}\).
Exemplo\(\PageIndex{6}\): Determining a Model for Tides
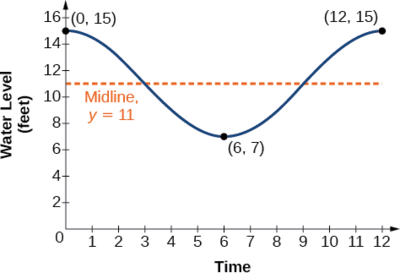
A altura da maré em uma pequena cidade litorânea é medida ao longo de um paredão. Os níveis de água oscilam entre 7 pés na maré baixa e 15 pés na maré alta. Em um determinado dia, a maré baixa ocorreu às 6 da manhã e a maré alta ocorreu ao meio-dia. Aproximadamente a cada 12 horas, o ciclo se repete. Encontre uma equação para modelar os níveis da água.
Solução
Como o nível da água varia de 7 pés a 15 pés, podemos calcular a amplitude como
\[ \begin{align*} |A| &=| \frac{(15−7)}{2} | \\ & =4 \end{align*}\]
O ciclo se repete a cada 12 horas; portanto,\(B\) é
\[\begin{align*} \dfrac{2π}{12}=\dfrac{π}{6} \end{align*}\]
Há uma tradução vertical de\(\frac{(15+8)}{2}=11.5\). Como o valor da função está no máximo em\(t=0\), usaremos a função cosseno, com o valor positivo para\(A\).
\[y=4 \cos (\dfrac{π}{6}) t+11 \nonumber\]
Veja a Figura\(\PageIndex{11}\).
Exercício\(\PageIndex{3}\):
A temperatura diária no mês de março em uma determinada cidade varia de baixa\(24°F\) a alta de\(40°F.\) Encontre uma função senoidal para modelar a temperatura diária e esboçar o gráfico. Aproximadamente a hora em que a temperatura atinge o ponto de congelamento.\(32 °F.\) Deixe\(t=0\) corresponder ao meio-dia.
- Responda
-
\[y=8 \sin (\frac{π}{12}t)+32 \nonumber\]
A temperatura chega a zero ao meio-dia e à meia-noite.
Exercício\(\PageIndex{4}\): Interpreting the Periodic Behavior Equation
A pressão arterial média de uma pessoa é modelada pela função\(f(t)=20 \sin (160πt)+100\), onde\(f(t)\) representa a pressão arterial de cada vez\(t\), medida em minutos. Interprete a função em termos de período e frequência. Desenhe o gráfico e encontre a leitura da pressão arterial.
Análise
A pressão arterial de\(\frac{120}{80}\) é considerada normal. O número superior é a leitura máxima ou sistólica, que mede a pressão nas artérias quando o coração se contrai. O número inferior é a leitura mínima ou diastólica, que mede a pressão nas artérias à medida que o coração relaxa entre as batidas, reabastecendo-se com sangue. Assim, a pressão arterial normal pode ser modelada por uma função periódica com um máximo de 120 e um mínimo de 80.
Exemplo\(\PageIndex{7}\): Interpreting the Periodic Behavior Equation
A pressão arterial média de uma pessoa é modelada pela função\(f(t)=20 \sin (160πt)+100\), onde\(f(t)\) representa a pressão arterial de cada vez\(t\), medida em minutos. Interprete a função em termos de período e frequência. Desenhe o gráfico e encontre a leitura da pressão arterial.
Solução
O período é dado por
\[\begin{align*} \dfrac{2π}{ω} & = \dfrac{2π}{160π} \\ &=\dfrac{1}{80} \end{align*}\]
Em uma função de pressão arterial, a frequência representa o número de batimentos cardíacos por minuto. A frequência é o recíproco do período e é dada por
\[\begin{align*} \dfrac{ω}{2π} & = \dfrac{160π}{2π} \\ & =80 \end{align*}\]
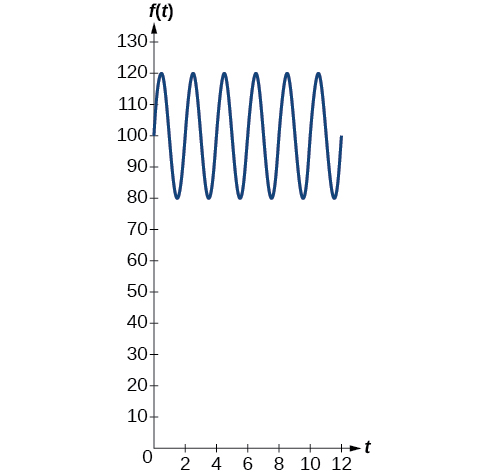
Análise
A pressão arterial de\(\frac{120}{80}\) é considerada normal. O número superior é a leitura máxima ou sistólica, que mede a pressão nas artérias quando o coração se contrai. O número inferior é a leitura mínima ou diastólica, que mede a pressão nas artérias à medida que o coração relaxa entre as batidas, reabastecendo-se com sangue. Assim, a pressão arterial normal pode ser modelada por uma função periódica com um máximo de 120 e um mínimo de 80.
Modelagem de funções de movimento harmônico
O movimento harmônico é uma forma de movimento periódico, mas há fatores a serem considerados que diferenciam os dois tipos. Enquanto as aplicações gerais de movimento periódico percorrem seus períodos sem interferência externa, o movimento harmônico requer uma força de restauração. Exemplos de movimento harmônico incluem molas, força gravitacional e força magnética.
Movimento harmônico simples
Um tipo de movimento descrito como movimento harmônico simples envolve uma força restauradora, mas pressupõe que o movimento continuará para sempre. Imagine um objeto pesado pendurado em uma mola. Quando esse objeto não é perturbado, dizemos que o objeto está em repouso ou em equilíbrio. Se o objeto for puxado para baixo e depois liberado, a força da mola o puxa de volta ao equilíbrio e o movimento harmônico começa. A força restauradora é diretamente proporcional ao deslocamento do objeto do seu ponto de equilíbrio. Quando\(t=0,d=0.\)
MOVIMENTO HARMÔNICO SIMPLES
Vemos que equações de movimento harmônico simples são dadas em termos de deslocamento:
\[d=a \cos (ωt) \; \text{or} \; d=a \sin (ωt) \]
onde\(| a |\) é a amplitude,\(\frac{2π}{ω}\) é o período e\(\frac{ω}{2π}\) é a frequência ou o número de ciclos por unidade de tempo.
Exercício\(\PageIndex{5}\): Finding the Displacement, Period, and Frequency, and Graphing a Function
Para cada uma das funções fornecidas:
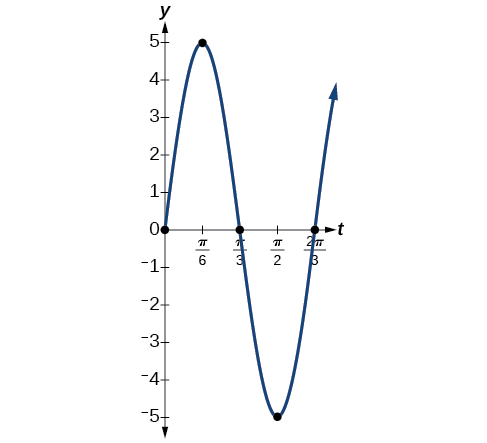
- \(y=5 \sin (3t)\)
- \(y=6 \cos (πt)\)
- \(y=5 \cos (\frac{π}{2}) t\)
aborde as seguintes questões:
- Encontre o deslocamento máximo de um objeto.
- Encontre o período ou o tempo necessário para uma vibração.
- Encontre a frequência.
- Esboce o gráfico.
- Responda a
-
- O deslocamento máximo é igual à amplitude,\( |a|\), que é 5.
- O período é\(\frac{2π}{ω}=\frac{2π}{3}\).
- A frequência é dada como\(\frac{ω}{2π}=\frac{3}{2π}\).
- Veja a Figura\(\PageIndex{13}\). O gráfico indica os cinco pontos-chave.
- Resposta b
-
- O deslocamento máximo é\(6\).
- O período é\(\frac{2π}{ω}=\frac{2π}{π}=2.\)
- A frequência é\(\frac{ω}{2π}=\frac{π}{2π}=\frac{1}{2}.\)
- Veja a Figura\(\PageIndex{14}\).
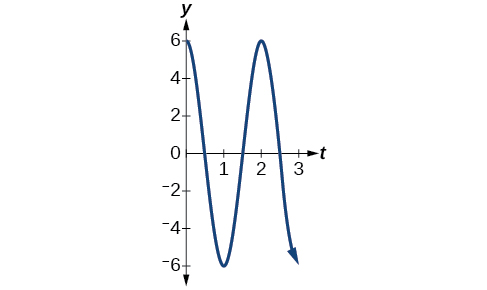
Figura\(\PageIndex{14}\) - Resposta c
-
- O deslocamento máximo é\(5\).
- O período é\(\frac{2π}{ω}=\frac{2π}{\frac{π}{2}}=4\).
- A frequência é\(\frac{1}{4}.\)
- Veja a Figura\(\PageIndex{15}\).
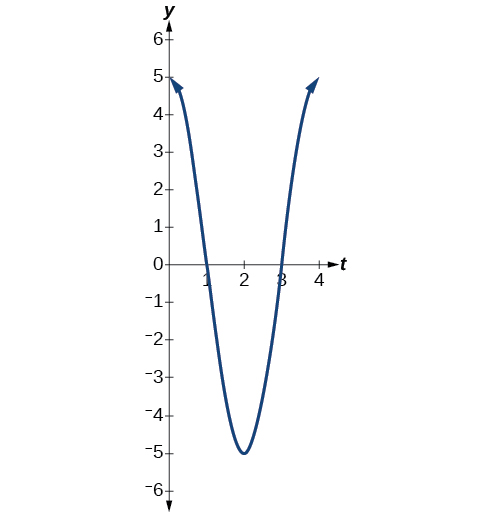
Figura\(\PageIndex{15}\)
Movimento harmônico amortecido
Na realidade, um pêndulo não balança para frente e para trás para sempre, nem um objeto em uma mola salta para cima e para baixo para sempre. Eventualmente, o pêndulo para de balançar e o objeto para de saltar e ambos retornam ao equilíbrio. O movimento periódico no qual uma força dissipadora de energia, ou fator de amortecimento, atua é conhecido como movimento harmônico amortecido. O atrito é normalmente o fator de amortecimento.
Em física, várias fórmulas são usadas para contabilizar o fator de amortecimento no objeto em movimento. Algumas delas são fórmulas baseadas em cálculo que envolvem derivadas. Para nossos propósitos, usaremos fórmulas para modelos básicos de movimento harmônico amortecido.
Definição: MOVIMENTO HARMÔNICO AMORTECIDO
No movimento harmônico amortecido, o deslocamento de um objeto oscilante de sua posição de repouso no momento\(t\) é dado como
\[ f(t)=ae^{−ct} \sin (ωt) \; \text{ or} \; f(t)=ae^{−ct} \cos (ωt)\]
onde\(c\) é um fator de amortecimento,\(|a|\) é o deslocamento inicial e\(\frac{2π}{ω}\) é o período.
Exemplo\(\PageIndex{8}\): Modeling Damped Harmonic Motion
Modele as equações que se encaixam nos dois cenários e use um utilitário gráfico para representar graficamente as funções: dois sistemas de mola de massa exibem movimento harmônico amortecido a uma frequência de 0,5 ciclos por segundo. Ambos têm um deslocamento inicial de 10 cm. O primeiro tem um fator de amortecimento de 0,5 e o segundo tem um fator de amortecimento de 0,1.
Solução
No momento\(t=0\), o deslocamento é de no máximo 10 cm, o que exige a função cosseno. A função cosseno será aplicada aos dois modelos.
Recebemos a frequência\(f=\frac{ω}{2π}\) de 0,5 ciclos por segundo. Assim,
\[\begin{align*} \dfrac{ω}{2π} &=0.5 \\ ω&=(0.5)2π \\ &=π \end{align*}\]
O primeiro sistema de mola tem um fator de amortecimento de\(c=0.5\). Seguindo o modelo geral para movimento harmônico amortecido, temos
\[f(t)=10e^{−0.5t} \cos (πt) \nonumber\]
A figura\(\PageIndex{16}\) modela o movimento do primeiro sistema de molas.
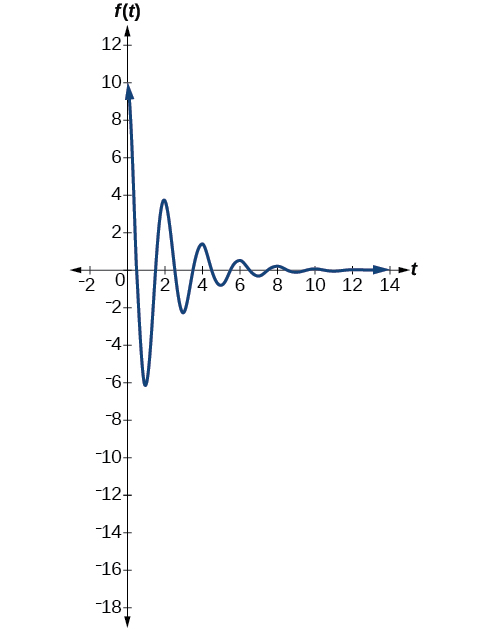
O segundo sistema de mola tem um fator de amortecimento de\(c=0.1\) e pode ser modelado como
\[f(t)=10e^{−0.1t} \cos (πt)\]
A figura\(\PageIndex{17}\) modela o movimento do segundo sistema de molas.
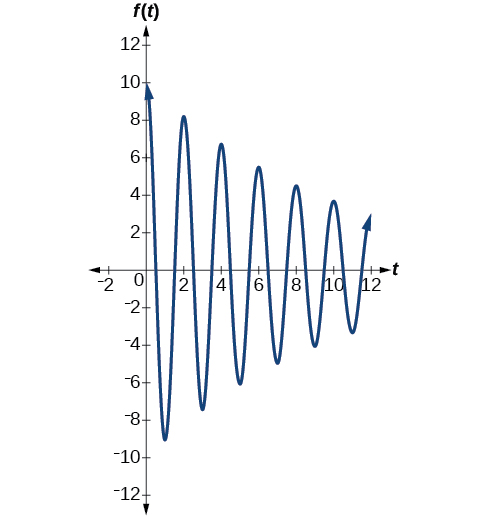
Análise
Observe os diferentes efeitos da constante de amortecimento. Os valores locais máximo e mínimo da função com o fator de amortecimento\(c=0.5\) diminuem muito mais rapidamente do que os da função com\(c=0.1\).
Exercício\(\PageIndex{6}\): Finding a Cosine Function that Models Damped Harmonic Motion
Encontre e represente graficamente uma função do formulário\(y=ae^{−ct} \cos (ωt)\) que modela as informações fornecidas.
- \(a=20,c=0.05,p=4\)
- \(a=2,c=1.5,f=3\)
Solução
Substitua os valores fornecidos no modelo. Lembre-se de que o período é\(\frac{2π}{ω}\) e a frequência é\(\frac{ω}{2π}\).
- \(y=20e^{−0.05t} \cos (\frac{π}{2}t).\)Veja a Figura\(\PageIndex{18}\).
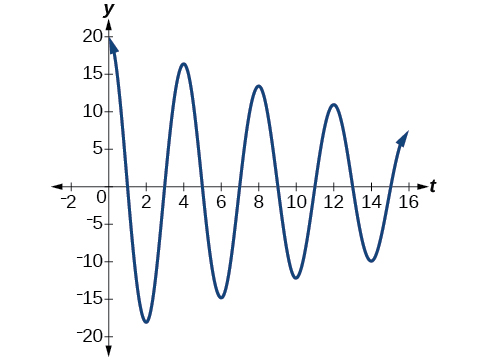
Figura\(\PageIndex{18}\) - \(y=2e^{−1.5t} \cos (6πt).\)Veja a Figura\(\PageIndex{19}\).
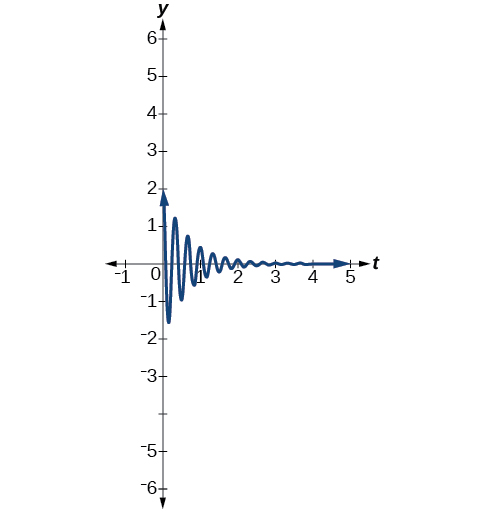
Figura\(\PageIndex{19}\)
Exercício\(\PageIndex{7}\)
A equação a seguir representa um modelo de movimento harmônico amortecido:\(f(t)=5e^{−6t} \cos (4t)\) Encontre o deslocamento inicial, a constante de amortecimento e a frequência.
- Responda
-
deslocamento inicial =6, constante de amortecimento = -6, frequência =\(\frac{2}{π}\)
Exemplo\(\PageIndex{9}\): Finding a Sine Function that Models Damped Harmonic Motion
Encontre e represente graficamente uma função do formulário\(y=ae^{−ct} \sin (ωt)\) que modela as informações fornecidas.
- \(a=7,c=10,p=\frac{π}{6}\)
- \(a=0.3,c=0.2,f=20\)
Solução
Calcule o valor de\(ω\) e substitua os valores conhecidos no modelo.
- Como o período é\(\frac{2π}{ω}\), temos
\[\begin{align*} \dfrac{π}{6} &=\dfrac{2π}{ω} \\ ωπ &=6(2π) \\ ω &=12 \end{align*}\]
O fator de amortecimento é dado como 10 e a amplitude é 7. Assim, o modelo é\(y=7e^{−10t} \sin (12t)\). Veja a Figura\(\PageIndex{20}\).
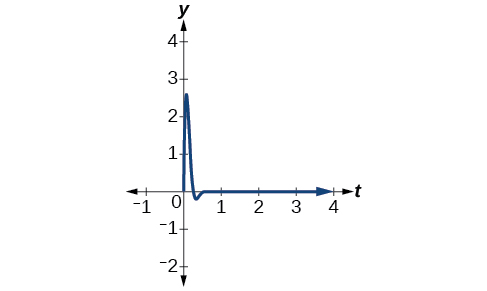
Figura\(\PageIndex{20}\) - Como frequência é\(\frac{ω}{2π}\), temos
\[\begin{align*} 20 &=\dfrac{ω}{2π} \\ 40π &=ω \end{align*}\]
O fator de amortecimento é dado como\(0.2\) e a amplitude é\(0.3.\) O modelo é\(y=0.3e^{−0.2t} \sin (40πt).\) Veja a Figura\(\PageIndex{21}\).
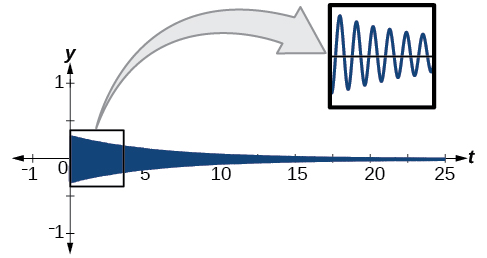
Figura\(\PageIndex{21}\)
Análise
Uma comparação dos dois últimos exemplos ilustra como escolhemos entre as funções seno ou cosseno para modelar critérios senoidais. Vemos que a função cosseno está no deslocamento máximo quando\(t=0\), e a função seno está no ponto de equilíbrio quando,\(t=0.\) por exemplo, considere a equação\(y=20e^{−0.05t} \cos (\frac{π}{2}t)\) de Example. Podemos ver no gráfico quando\(t=0,y=20,\) qual é a amplitude inicial. Verifique isso\(t=0\) configurando a equação do cosseno:
\[ \begin{align*} y &=20e^{−0.05(0)} \cos (\frac{π}{2})(0) \\ &=20(1)(1) \\ & =20 \end{align*}\]
O uso da função seno produz
\[\begin{align*} y &=20e^{−0.05(0)} \sin (\frac{π}{2})(0) \\ & =20(1)(0) \\ &=0 \end{align*}\]
Assim, o cosseno é a função correta.
Exercício\(\PageIndex{8}\):
Escreva a equação para o movimento harmônico amortecido dado\(a=10,c=0.5\), e\(p=2.\)
- Responda
-
\(y=10e^{−0.5t} \cos (πt)\)
Exemplo\(\PageIndex{10}\): Modeling the Oscillation of a Spring
Uma mola medindo 10 polegadas de comprimento natural é comprimida em 5 polegadas e liberada. Ele oscila uma vez a cada 3 segundos e sua amplitude diminui em 30% a cada segundo. Encontre uma equação que modela a posição da mola\(t\) segundos após ser liberada.
Solução
A amplitude começa em 5 pol. e diminui 30% a cada segundo. Como a mola está inicialmente comprimida, escreveremos A como um valor negativo. Podemos escrever a porção de amplitude da função como
\[A(t)=5(1−0.30)^t \nonumber\]
Colocamos\((1−0.30)^t\) no formulário da\(e^{ct}\) seguinte forma:
\[\begin{align*} 0.7 &=e^c \\ c &= \ln .7 \\ c & =−0.357 \end{align*}\]
Agora vamos abordar o período. A mola percorre suas posições a cada 3 segundos, esse é o período, e podemos usar a fórmula para encontrar ômega.
\[\begin{align*} 3 &= \dfrac{2π}{ω} \\ ω &= \dfrac{2π}{3} \end{align*}\]
O comprimento natural de 10 polegadas é a linha média. Usaremos a função cosseno, já que a mola começa com seu deslocamento máximo. Essa parte da equação é representada como
\[y=\cos (\dfrac{2π}{3}t)+10 \nonumber\]
Finalmente, juntamos as duas funções. Nosso modelo para a posição da mola em\(t\) segundos é dado como
\[y=−5e^{−0.357t} \cos (\dfrac{2π}{3}t)+10 \nonumber\]
Veja o gráfico na Figura\(\PageIndex{22}\).
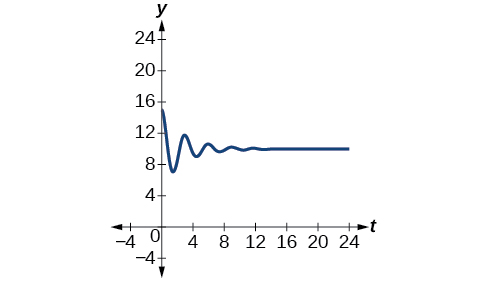
Exercício\(\PageIndex{9}\)
Uma massa suspensa de uma mola é elevada a uma distância de 5 cm acima de sua posição de repouso. A massa é liberada de vez em quando\(t=0\) e pode oscilar. Após o\(\frac{1}{3}\) segundo, observa-se que a massa retorna à sua posição mais alta. Encontre uma função para modelar esse movimento em relação à sua posição inicial de repouso.
- Responda
-
\(y=5 \cos (6πt)\)
De acordo com os critérios fornecidos
Uma corda de guitarra é dedilhada e vibra em um movimento harmônico amortecido. A corda é puxada e deslocada a 2 cm de sua posição de repouso. Após 3 segundos, o deslocamento da corda mede 1 cm. Encontre a constante de amortecimento.
Solução
O fator de deslocamento representa a amplitude e é determinado pelo coeficiente\(ae^{−ct}\) no modelo para movimento harmônico amortecido. A constante de amortecimento está incluída no termo\(e^{−ct}\). Sabe-se que após 3 segundos, o máximo local mede a metade de seu valor original. Portanto, temos a equação
\[ae^{−c(t+3)}=\dfrac{1}{2} ae^{−ct}\]
Use álgebra e as leis dos expoentes para resolver\(c\).
\[\begin{array}{cl} ae^{−c(t+3)}=\frac{1}{2}ae^{−ct} \\ e^{−ct}⋅e^{−3c}=\frac{1}{2}e^{−ct} & \text{Divide out } a. \\ e^{−3c}=\frac{1}{2} & \text{Divide out }e^{−ct}. \\ e^{3c}=2 & \text{Take reciprocals.} \end{array}\]
Em seguida, use as leis dos logaritmos.
\[\begin{align*} e^{3c} &=2 \\ 3c &=\ln 2 \\ c & =\frac{\ln 2}{3} \end{align*}\]
A constante de amortecimento é\(\frac{\ln 2}{3}\).
Curvas delimitadoras em movimento harmônico
Os gráficos de movimento harmônico podem ser delimitados por curvas delimitadoras. Quando uma função tem uma amplitude variável, de forma que a amplitude aumenta e diminui várias vezes em um período, podemos determinar as curvas delimitadoras de parte da função.
Exemplo\(\PageIndex{12}\): Graphing an Oscillating Cosine Curve
Faça um gráfico da função\(f(x)=\cos (2πx) \cos (16πx)\).
Solução
O gráfico produzido por essa função será mostrado em duas partes. O primeiro gráfico será a função exata\(f(x)\) (veja a Figura\(\PageIndex{23; top}\);) e o segundo gráfico é a função exata\(f(x)\) mais uma função delimitadora (veja a Figura\(\PageIndex{23; bottom}\)). Os gráficos parecem bem diferentes.

Figura\(\PageIndex{23}\)
Análise
As curvas\(y=\cos (2πx)\) e\(y=−\cos (2πx)\) são curvas delimitadoras: elas limitam a função de cima para baixo, traçando os pontos altos e baixos. O gráfico de movimento harmônico fica dentro das curvas delimitadoras. Este é um exemplo de uma função cuja amplitude não só diminui com o tempo, mas na verdade aumenta e diminui várias vezes em um período.
Equações-chave
| Forma padrão da equação senoidal | \(y=A \sin (Bt−C)+D \text{ or } y=A \cos (Bt−C)+D\) |
| Movimento harmônico simples | \(d=a \cos (ωt) \text{ or } d=a \sin (ωt) \) |
| Movimento harmônico amortecido | \(f(t)=ae^{−ct} \sin (ωt) \text{ or } f(t)=ae^{−ct} \cos (ωt)\) |
Conceitos-chave
- As funções sinusoidais são representadas pelos gráficos de seno e cosseno. Na forma padrão, podemos encontrar a amplitude, o período e as mudanças horizontais e verticais. Veja o exemplo e o exemplo.
- Use pontos-chave para representar graficamente uma função senoidal. Os cinco pontos-chave incluem os valores mínimo e máximo e os valores da linha média. Veja o exemplo.
- As funções periódicas podem modelar eventos que reocorrem em ciclos definidos, como as fases da lua, os ponteiros de um relógio e as estações do ano. Veja exemplo, exemplo, exemplo e exemplo.
- As funções de movimento harmônico são modeladas a partir de dados fornecidos. Semelhante às aplicações de movimento periódico, o movimento harmônico requer uma força de restauração. Os exemplos incluem a força gravitacional e o movimento da mola ativados pelo peso. Veja o exemplo.
- O movimento harmônico amortecido é uma forma de comportamento periódico afetada por um fator de amortecimento. Fatores de dissipação de energia, como atrito, fazem com que o deslocamento do objeto encolha. Veja exemplo, exemplo, exemplo, exemplo e exemplo.
- As curvas delimitadoras delineiam o gráfico do movimento harmônico com valores máximos e mínimos variáveis. Veja o exemplo.


