4.4: Gráficos de funções logarítmicas
- Page ID
- 189218
- Identifique o domínio de uma função logarítmica.
- Representar graficamente funções logarítmicas.
Na seção sobre gráficos de funções exponenciais, vimos como a criação de uma representação gráfica de um modelo exponencial nos dá outra camada de visão para prever eventos futuros. Como os gráficos logarítmicos nos dão uma visão das situações? Como toda função logarítmica é a função inversa de uma função exponencial, podemos pensar em cada saída em um gráfico logarítmico como a entrada para a equação exponencial inversa correspondente. Em outras palavras, os logaritmos dão a causa de um efeito.
Para ilustrar, suponha que invistamos\($2500\) em uma conta que ofereça uma taxa de juros anual de 5%, composta continuamente. Já sabemos que o saldo em nossa conta para qualquer ano\(t\) pode ser encontrado com a equação\(A=2500e^{0.05t}\).
Mas e se quiséssemos saber o ano com algum saldo? Precisaríamos criar uma nova função correspondente trocando a entrada e a saída; portanto, precisaríamos criar um modelo logarítmico para essa situação. Ao representar graficamente o modelo, podemos ver a saída (ano) de qualquer entrada (saldo da conta). Por exemplo, e se quiséssemos saber quantos anos seriam necessários para que nosso investimento inicial dobrasse? A figura\(\PageIndex{1}\) mostra esse ponto no gráfico logarítmico.
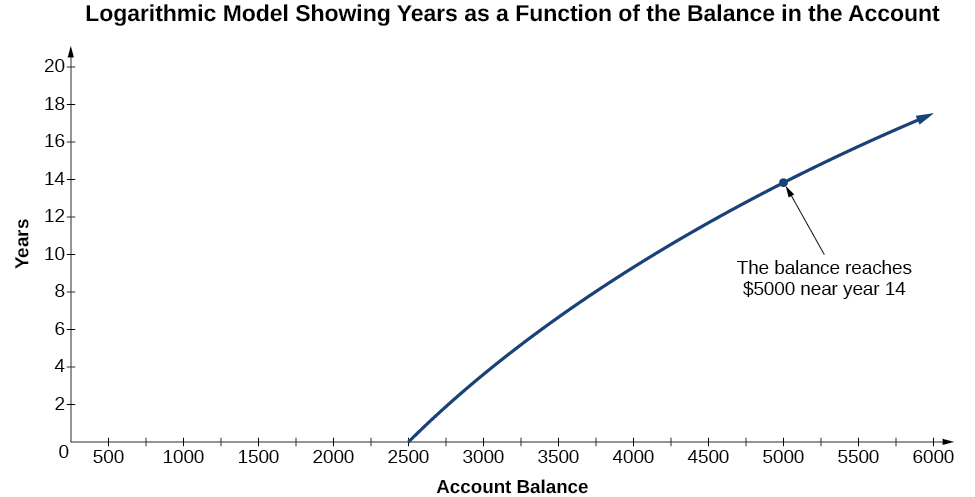
Nesta seção, discutiremos os valores para os quais uma função logarítmica é definida e, em seguida, voltaremos nossa atenção para a representação gráfica da família de funções logarítmicas.
Encontrando o domínio de uma função logarítmica
Antes de trabalhar com gráficos, examinaremos o domínio (o conjunto de valores de entrada) para o qual a função logarítmica está definida.
Lembre-se de que a função exponencial é definida como\(y=b^x\) para qualquer número real\(x\) e constante\(b>0\),\(b≠1\), onde
- O domínio de\(y\) é\((−\infty,\infty)\).
- O alcance de\(y\) é\((0,\infty)\).
Na última seção, aprendemos que a função logarítmica\(y={\log}_b(x)\) é o inverso da função exponencial\(y=b^x\). Então, como funções inversas:
- O domínio de\(y={\log}_b(x)\) é o intervalo de\(y=b^x\):\((0,\infty)\).
- O alcance de\(y={\log}_b(x)\) é o domínio de\(y=b^x\):\((−\infty,\infty)\).
As transformações da função principal\(y={\log}_b(x)\) se comportam de forma semelhante às de outras funções. Assim como com outras funções principais, podemos aplicar os quatro tipos de transformações — deslocamentos, alongamentos, compressões e reflexões — à função principal sem perda de forma.
Em Gráficos de Funções Exponenciais, vimos que certas transformações podem alterar o alcance de\(y=b^x\). Da mesma forma, aplicar transformações à função principal\(y={\log}_b(x)\) pode alterar o domínio. Ao encontrar o domínio de uma função logarítmica, portanto, é importante lembrar que o domínio consiste apenas em números reais positivos. Ou seja, o argumento da função logarítmica deve ser maior que zero.
Por exemplo, considere\(f(x)={\log}_4(2x−3)\). Essa função é definida para qualquer valor de\(x\) tal que o argumento, nesse caso\(2x−3\), seja maior que zero. Para encontrar o domínio, configuramos uma desigualdade e resolvemos\(x\):
\[\begin{align*} 2x-3&> 0 \qquad \text {Show the argument greater than zero}\\ 2x&> 3 \qquad \text{Add 3} \\ x&> 1.5 \qquad \text{Divide by 2} \\ \end{align*}\]
Na notação de intervalo, o domínio de\(f(x)={\log}_4(2x−3)\) é\((1.5,\infty)\).
- Configure uma desigualdade mostrando o argumento maior que zero.
- Resolva para\(x\).
- Escreva o domínio em notação de intervalo.
Qual é o domínio de\(f(x)={\log}_2(x+3)\)?
Solução
A função logarítmica é definida somente quando a entrada é positiva, então essa função é definida quando\(x+3>0\). Resolvendo essa desigualdade,
\[\begin{align*} x+3&> 0 \qquad \text{The input must be positive}\\ x&> -3 \qquad \text{Subtract 3} \end{align*}\]
O domínio de\(f(x)={\log}_2(x+3)\) é\((−3,\infty)\).
Qual é o domínio de\(f(x)={\log}_5(x−2)+1\)?
- Responda
-
\((2,\infty)\)
Qual é o domínio de\(f(x)=\log(5−2x)\)?
Solução
A função logarítmica é definida somente quando a entrada é positiva, então essa função é definida quando\(5–2x>0\). Resolvendo essa desigualdade,
\[\begin{align*} 5-2x&> 0 \qquad \text{The input must be positive}\\ -2x&> -5 \qquad \text{Subtract 5}\\ x&< \dfrac{5}{2} \qquad \text{Divide by -2 and switch the inequality} \end{align*}\]
O domínio de\(f(x)=\log(5−2x)\) é\(\left(–\infty,\dfrac{5}{2}\right)\).
Qual é o domínio de\(f(x)=\log(x−5)+2\)?
- Responda
-
\((5,\infty)\)
Representação gráfica de funções logarítmicas
Agora que temos uma ideia do conjunto de valores para o qual uma função logarítmica é definida, passamos a representar graficamente funções logarítmicas. A família de funções logarítmicas inclui a função principal\(y={\log}_b(x)\) junto com todas as suas transformações: mudanças, alongamentos, compressões e reflexões.
Começamos com a função principal\(y={\log}_b(x)\). Como cada função logarítmica dessa forma é o inverso de uma função exponencial com a forma\(y=b^x\), seus gráficos serão reflexos um do outro ao longo da linha\(y=x\). Para ilustrar isso, podemos observar a relação entre os valores de entrada e saída de\(y=2^x\) e seu equivalente\(x={\log}_2(y)\) na Tabela\(\PageIndex{1}\).
| \(x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|---|---|---|
| \(2^x=y\) | \(\dfrac{1}{8}\) | \(\dfrac{1}{4}\) | \(\dfrac{1}{2}\) | \(1\) | \(2\) | \(4\) | \(8\) |
| \({\log}_2(y)=x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
Usando as entradas e saídas da Tabela\(\PageIndex{1}\), podemos construir outra tabela para observar a relação entre os pontos nos gráficos das funções inversas\(f(x)=2^x\)\(g(x)={\log}_2(x)\) e. Veja a tabela\(\PageIndex{2}\).
| \(f(x)=2^x\) | \(\left(−3,\dfrac{1}{8}\right)\) | \(\left(−2,\dfrac{1}{4}\right)\) | \(\left(−1,\dfrac{1}{2}\right)\) | \((0,1)\) | \((1,2)\) | \((2,4)\) | \((3,8)\) |
|---|---|---|---|---|---|---|---|
| \(g(x)={\log}_2(x)\) | \(\left(\dfrac{1}{8},−3\right)\) | \(\left(\dfrac{1}{4},−2\right)\) | \(\left(\dfrac{1}{2},−1\right)\) | \((1,0)\) | \((2,1)\) | \((4,2)\) | \((8,3)\) |
Como seria de esperar, as\(y\) coordenadas\(x\) - e -são invertidas para as funções inversas. A figura\(\PageIndex{2}\) mostra o gráfico de\(f\)\(g\) e.
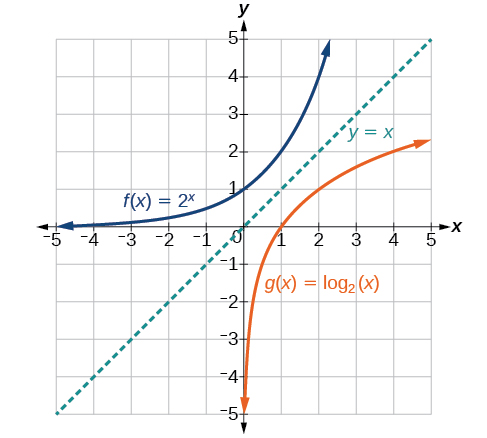
Observe o seguinte no gráfico:
- \(f(x)=2^x\)tem um\(y\) intercepto -em\((0,1)\) e\(g(x)={\log}_2(x)\) tem um\(x\) - intercepto em\((1,0)\).
- O domínio de\(f(x)=2^x\),\((−\infty,\infty)\), é o mesmo que o intervalo de\(g(x)={\log}_2(x)\).
- O intervalo de\(f(x)=2^x\),\((0,\infty)\), é o mesmo que o domínio de\(g(x)={\log}_2(x)\).
Para qualquer número real\(x\) e constante\(b>0\)\(b≠1\), podemos ver as seguintes características no gráfico de\(f(x)={\log}_b(x)\):
- função um para um
- assíntota vertical:\(x=0\)
- domínio:\((0,\infty)\)
- alcance:\((−\infty,\infty)\)
- \(x\)- interceptar:\((1,0)\) e ponto-chave\((b,1)\)
- \(y\)-interceptar: nenhum
- aumentando se\(b>1\)
- diminuindo se\(0<b<1\)
Veja a Figura\(\PageIndex{3}\).
A figura\(\PageIndex{4}\) mostra como a alteração da base\(b\) em\(f(x)={\log}_b(x)\) pode afetar os gráficos. Observe que os gráficos se comprimem verticalmente à medida que o valor da base aumenta. (Nota: lembre-se de que a função\(\ln(x)\) tem base\(e≈2.718\).)
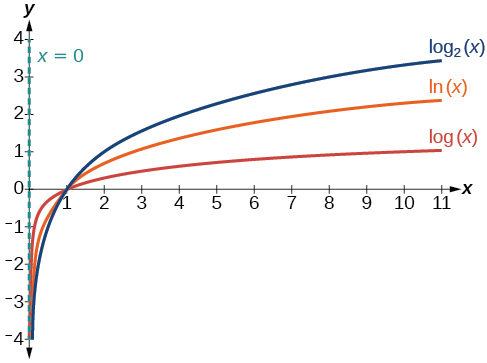
- Desenhe e rotule a assíntota vertical,\(x=0\).
- Faça um gráfico do intercepto x,\((1,0)\).
- Faça um gráfico do ponto chave\((b,1)\).
- Desenhe uma curva suave entre os pontos.
- Indique o domínio\((0,\infty)\), o intervalo e a assíntota vertical,\(x=0\).\((−\infty,\infty)\)
Gráfico\(f(x)={\log}_5(x)\). Indique o domínio, o alcance e a assíntota.
Solução
Antes de representar graficamente, identifique o comportamento e os pontos-chave do gráfico.
- Como\(b=5\) é maior que um, sabemos que a função está aumentando. A cauda esquerda do gráfico se aproximará da assíntota\(x=0\) vertical e a cauda direita aumentará lentamente sem limite.
- O\(x\) intercepto -é\((1,0)\).
- O ponto chave\((5,1)\) está no gráfico.
- Desenhamos e rotulamos a assíntota, traçamos e rotulamos os pontos e desenhamos uma curva suave através dos pontos (veja a Figura\(\PageIndex{5}\)).
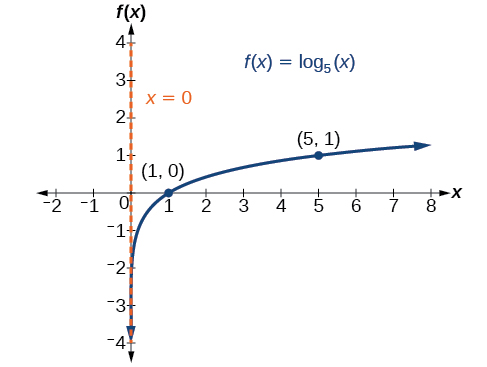
O domínio é\((0,\infty)\), o intervalo é\((−\infty,\infty)\) e a assíntota vertical é\(x=0\).
Gráfico\(f(x)={\log}_{\tfrac{1}{5}}(x)\). Indique o domínio, o alcance e a assíntota.
- Responda
-
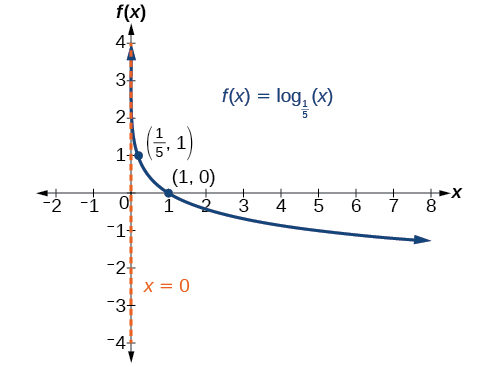
Figura\(\PageIndex{6}\) O domínio é\((0,\infty)\), o intervalo é\((−\infty,\infty)\) e a assíntota vertical é\(x=0\).
Representação gráfica de transformações de funções logarítmicas
Como mencionamos no início da seção, as transformações dos gráficos logarítmicos se comportam de forma semelhante às de outras funções principais. Podemos mudar, esticar, comprimir e refletir a função principal\(y={\log}_b(x)\) sem perda de forma.
Representando graficamente uma mudança horizontal de\(f(x) = log_b(x)\)
Quando uma constante\(c\) é adicionada à entrada da função principal\(f(x)={\log}_b(x)\), o resultado é uma\(c\) unidade de deslocamento horizontal na direção oposta ao sinal\(c\). Para visualizar os deslocamentos horizontais, podemos observar o gráfico geral da função principal\(f(x)={\log}_b(x)\) e para\(c>0\) ao lado do deslocamento para a esquerda e o deslocamento para a direita\(h(x)={\log}_b(x−c)\).\(g(x)={\log}_b(x+c)\) Veja a Figura\(\PageIndex{7}\).
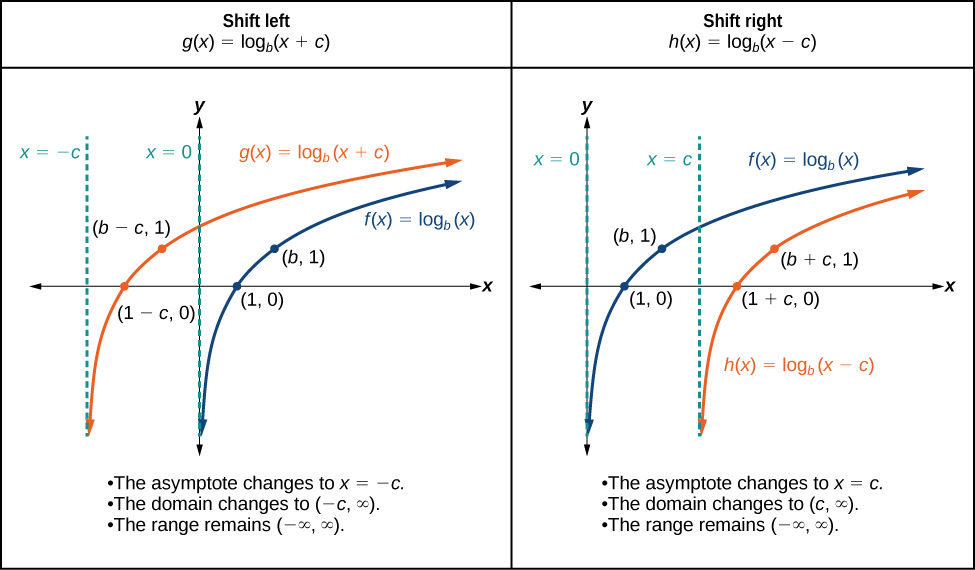
Para qualquer constante\(c\), a função\(f(x)={\log}_b(x+c)\)
- desloca a função principal para a\(y={\log}_b(x)\) esquerda\(c\) das unidades se\(c>0\).
- desloca a função principal para a\(y={\log}_b(x)\) direita,\(c\) unidades se\(c<0\).
- tem a assíntota vertical\(x=−c\).
- tem domínio\((−c,\infty)\).
- tem alcance\((−\infty,\infty)\).
- Identifique o deslocamento horizontal:
- Se\(c>0\), mude o gráfico das\(c\) unidades\(f(x)={\log}_b(x)\) esquerdas.
- Se\(c<0\), mude o gráfico das\(c\) unidades\(f(x)={\log}_b(x)\) corretas.
- Desenhe a assíntota vertical\(x=−c\).
- Identifique três pontos-chave da função principal. Encontre novas coordenadas para as funções deslocadas\(c\) subtraindo da\(x\) coordenada.
- Identifique os três pontos.
- O domínio é\((−c,\infty)\), o alcance é\((−\infty,\infty)\) e a assíntota vertical é\(x=−c\).
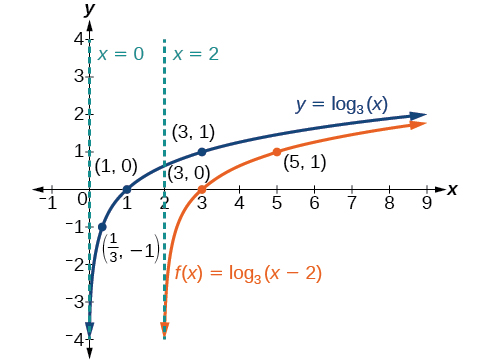
Desenhe o deslocamento horizontal\(f(x)={\log}_3(x−2)\) ao lado de sua função principal. Inclua os pontos-chave e as assíntotas no gráfico. Indique o domínio, o alcance e a assíntota.
Solução
Como a função é\(f(x)={\log}_3(x−2)\), notamos\(x+(−2)=x–2\).
Assim\(c=−2\), então\(c<0\). Isso significa que vamos mudar a função para a\(f(x)={\log}_3(x)\) direita em 2 unidades.
A assíntota vertical é\(x=−(−2)\) ou\(x=2\).
Considere os três pontos-chave da função principal\(\left(\dfrac{1}{3},−1\right)\)\((1,0)\),,\((3,1)\) e.
As novas coordenadas são encontradas adicionando\(2\) às\(x\) coordenadas.
Identifique os pontos\(\left(\dfrac{7}{3},−1\right)\)\((3,0)\),\((5,1)\) e.
O domínio é\((2,\infty)\), o intervalo é\((−\infty,\infty)\) e a assíntota vertical é\(x=2\).
Esboce um gráfico\(f(x)={\log}_3(x+4)\) ao lado de sua função principal. Inclua os pontos-chave e as assíntotas no gráfico. Indique o domínio, o alcance e a assíntota.
- Responda
-
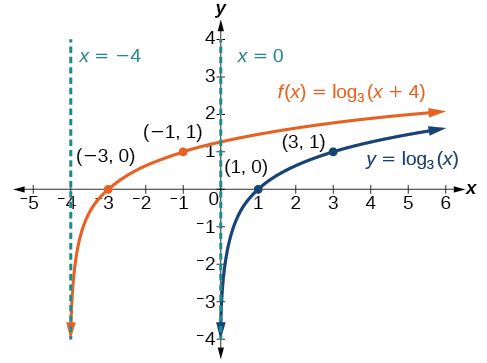
Figura\(\PageIndex{9}\) O domínio é\((−4,\infty)\), o alcance\((−\infty,\infty)\) e a assíntota\(x=–4\).
Representando graficamente uma mudança vertical de\(y = log_b(x)\)
Quando uma constante\(d\) é adicionada à função principal\(f(x)={\log}_b(x)\), o resultado é uma\(d\) unidade de deslocamento vertical na direção do sinal\(d\). Para visualizar os deslocamentos verticais, podemos observar o gráfico geral da função principal ao\(f(x)={\log}_b(x)\) lado do deslocamento para cima\(g(x)={\log}_b(x)+d\) e do deslocamento para baixo,\(h(x)={\log}_b(x)−d\) .Veja a Figura\(\PageIndex{10}\).
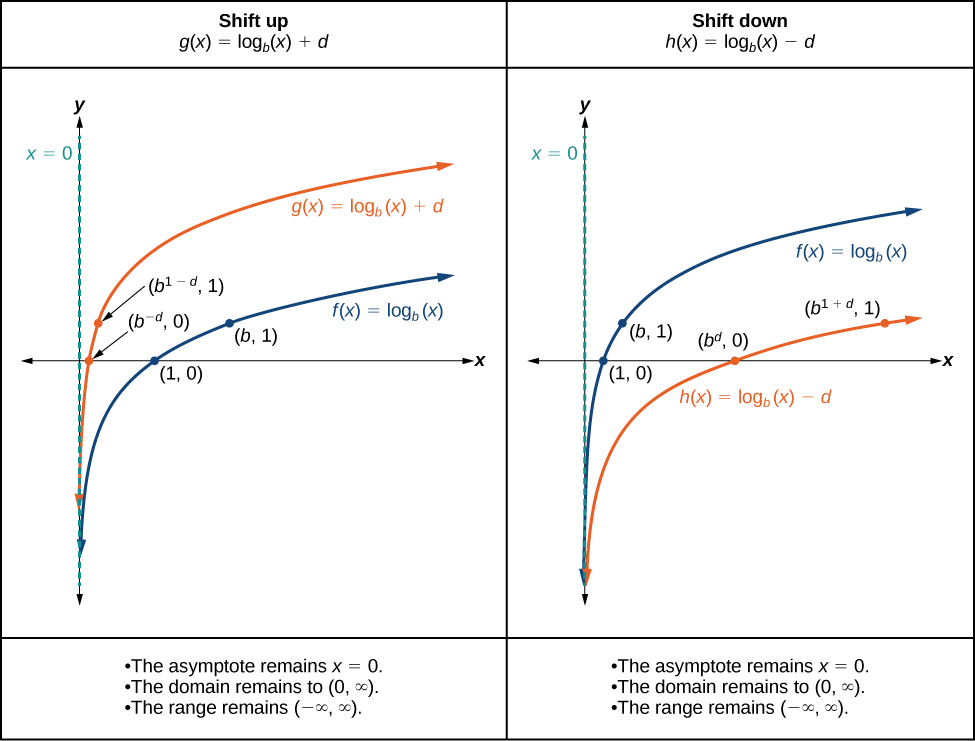
Para qualquer constante\(d\), a função\(f(x)={\log}_b(x)+d\)
- desloca a função principal\(y={\log}_b(x)\) para cima\(d\) unidades se\(d>0\).
- desloca a função principal\(y={\log}_b(x)\) para baixo\(d\) unidades se\(d<0\).
- tem a assíntota vertical\(x=0\).
- tem domínio\((0,\infty)\).
- tem alcance\((−\infty,\infty)\).
- Identifique a mudança vertical:
- Se\(d>0\), mude o gráfico das\(d\) unidades\(f(x)={\log}_b(x)\) para cima.
- Se\(d<0\), desloque o gráfico das\(d\) unidades\(f(x)={\log}_b(x)\) para baixo.
- Desenhe a assíntota vertical\(x=0\).
- Identifique três pontos-chave da função principal. Encontre novas coordenadas para as funções deslocadas adicionando\(d\) à\(y\) coordenada.
- Identifique os três pontos.
- O domínio é\((0,\infty)\), o intervalo é\((−\infty,\infty)\) e a assíntota vertical é\(x=0\).
Esboce um gráfico\(f(x)={\log}_3(x)−2\) ao lado de sua função principal. Inclua os pontos-chave e a assíntota no gráfico. Indique o domínio, o alcance e a assíntota.
Solução
Como a função é\(f(x)={\log}_3(x)−2\), notaremos\(d=–2\). Assim\(d<0\).
Isso significa que vamos mudar a função\(f(x)={\log}_3(x)\) para baixo em\(2\) unidades.
A assíntota vertical é\(x=0\).
Considere os três pontos-chave da função principal\(\left(\dfrac{1}{3},−1\right)\)\((1,0)\),,\((3,1)\) e.
As novas coordenadas são encontradas\(2\) subtraindo as coordenadas y.
Identifique os pontos\(\left(\dfrac{1}{3},−3\right)\)\((1,−2)\),\((3,−1)\) e.
O domínio é\((0,\infty)\), o intervalo é\((−\infty,\infty)\) e a assíntota vertical é\(x=0\).
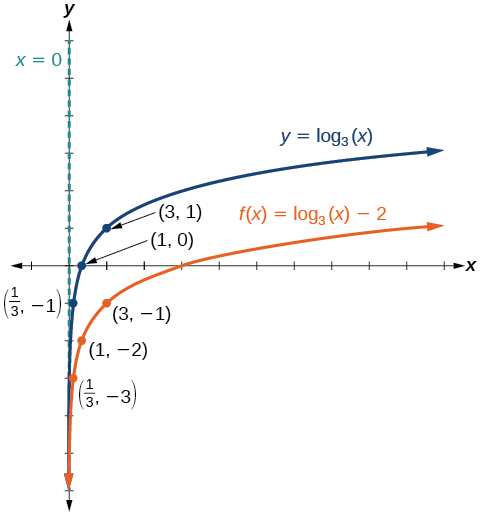
O domínio é\((0,\infty)\), o intervalo é\((−\infty,\infty)\) e a assíntota vertical é\(x=0\).
Esboce um gráfico\(f(x)={\log}_2(x)+2\) ao lado de sua função principal. Inclua os pontos-chave e a assíntota no gráfico. Indique o domínio, o alcance e a assíntota.
- Responda
-
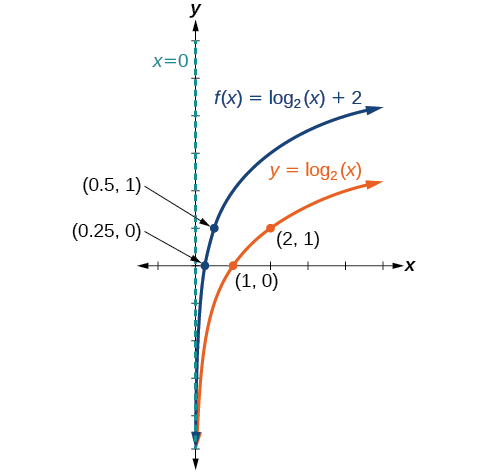
Figura\(\PageIndex{12}\) O domínio é\((0,\infty)\), o intervalo é\((−\infty,\infty)\) e a assíntota vertical é\(x=0\).
Representação gráfica de trechos e compressões de\(y = log_b(x)\)
Quando a função principal\(f(x)={\log}_b(x)\) é multiplicada por uma constante\(a>0\), o resultado é um alongamento ou compressão vertical do gráfico original. Para visualizar alongamentos e compressões, definimos\(a>1\) e observamos o gráfico geral da função principal\(f(x)={\log}_b(x)\) ao lado do alongamento vertical\(g(x)=a{\log}_b(x)\) e da compressão vertical,\(h(x)=\dfrac{1}{a}{\log}_b(x)\) .Veja a Figura\(\PageIndex{13}\).
Para qualquer constante\(a>1\), a função\(f(x)=a{\log}_b(x)\)
- alonga a função principal\(y={\log}_b(x)\) verticalmente por um fator de\(a\) if\(a>1\).
- comprime a função principal\(y={\log}_b(x)\) verticalmente por um fator de\(a\) if\(0<a<1\).
- tem a assíntota vertical\(x=0\).
- tem o\(x\) intercepto\((1,0)\) -.
- tem domínio\((0,\infty)\).
- tem alcance\((−\infty,\infty)\).
- Identifique o estiramento vertical ou as compressões:
- Se\(|a|>1\), o gráfico de\(f(x)={\log}_b(x)\) é esticado por um fator de\(a\) unidades.
- Se\(|a|<1\), o gráfico de\(f(x)={\log}_b(x)\) é comprimido por um fator de\(a\) unidades.
- Desenhe a assíntota vertical\(x=0\).
- Identifique três pontos-chave da função principal. Encontre novas coordenadas para as funções deslocadas multiplicando as coordenadas y por\(a\).
- Identifique os três pontos.
- O domínio é\((0,\infty)\), o intervalo é\((−\infty,\infty)\) e a assíntota vertical é\(x=0\).
Esboce um gráfico\(f(x)=2{\log}_4(x)\) ao lado de sua função principal. Inclua os pontos-chave e a assíntota no gráfico. Indique o domínio, o alcance e a assíntota.
Solução
Como a função é\(f(x)=2{\log}_4(x)\), notaremos\(a=2\).
Isso significa que ampliaremos a função\(f(x)={\log}_4(x)\) por um fator de\(2\).
A assíntota vertical é\(x=0\).
Considere os três pontos-chave da função principal\(\left(\dfrac{1}{4},−1\right)\)\((1,0)\),,\((4,1)\) e.
As novas coordenadas são encontradas multiplicando as\(y\) coordenadas por\(2\).
Identifique os pontos\(\left(\dfrac{1}{4},−2\right)\)\((1,0)\),\((4,2)\) e.
O domínio é\((0, \infty)\), o intervalo é\((−\infty,\infty)\) e a assíntota vertical é\(x=0\). Veja a Figura\(\PageIndex{14}\).
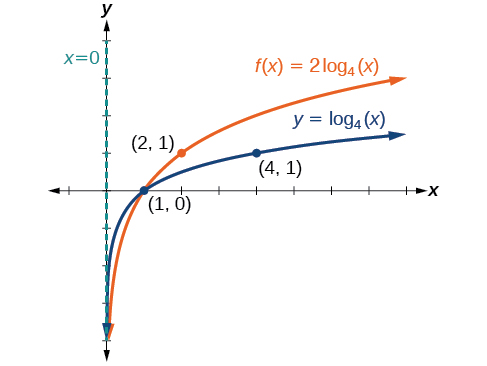
O domínio é\((0,\infty)\), o intervalo é\((−\infty,\infty)\) e a assíntota vertical é\(x=0\).
Esboce um gráfico\(f(x)=\dfrac{1}{2}{\log}_4(x)\) ao lado de sua função principal. Inclua os pontos-chave e a assíntota no gráfico. Indique o domínio, o alcance e a assíntota.
- Responda
-
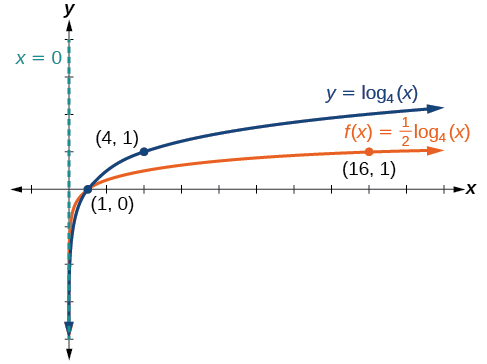
Figura\(\PageIndex{15}\) O domínio é\((0,\infty)\), o intervalo é\((−\infty,\infty)\) e a assíntota vertical é\(x=0\).
Esboce um gráfico de\(f(x)=5{\log}(x+2)\). Indique o domínio, o alcance e a assíntota.
Solução
Lembre-se: o que acontece entre parênteses acontece primeiro. Primeiro, movemos as\(2\) unidades para a esquerda do gráfico e, em seguida, esticamos a função verticalmente por um fator de\(5\), como na Figura\(\PageIndex{16}\). A assíntota vertical será deslocada para\(x=−2\). O\(x\) intercepto -será\((−1,0)\). O domínio será\((−2,\infty)\). Dois pontos ajudarão a dar a forma do gráfico:\((−1,0)\)\((8,5)\) e. Escolhemos\(x=8\) como coordenada x de um ponto para representar graficamente porque quando\(x=8\)\(x+2=10\),, a base do logaritmo comum.
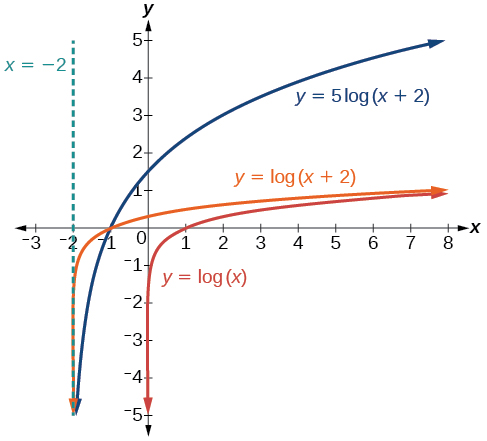
O domínio é\((−2,\infty)\), o intervalo é\((−\infty,\infty)\) e a assíntota vertical é\(x=−2\).
Esboce um gráfico da função\(f(x)=3{\log}(x−2)+1\). Indique o domínio, o alcance e a assíntota.
- Responda
-
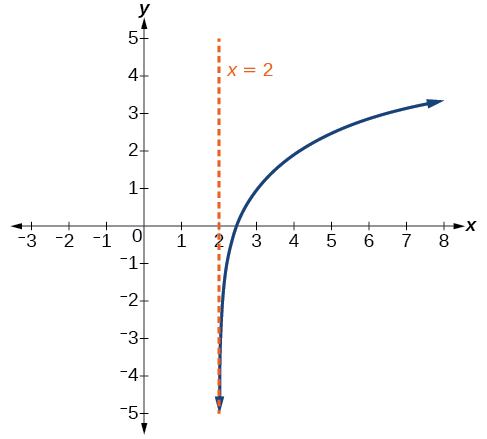
Figura\(\PageIndex{17}\) O domínio é\((2,\infty)\), o intervalo é\((−\infty,\infty)\) e a assíntota vertical é\(x=2\).
Representação gráfica de reflexões de\(f(x) = log_b(x)\)
Quando a função principal\(f(x)={\log}_b(x)\) é multiplicada por\(−1\), o resultado é uma reflexão sobre o\(x\) eixo. Quando a entrada é multiplicada por\(−1\), o resultado é uma reflexão sobre o\(y\) eixo. Para visualizar as reflexões\(b>1\), restringimos e observamos o gráfico geral da função principal\(f(x)={\log}_b(x)\) ao lado da reflexão sobre o\(x\) eixo\(g(x)=−{\log}_b(x)\) -e a reflexão sobre o\(y\) eixo -,\(h(x)={\log}_b(−x)\).
A função\(f(x)=−{\log}_b(x)\)
- reflete a função principal\(y={\log}_b(x)\) sobre o\(x\) eixo y.
- tem domínio\((0,\infty)\),\((−\infty,\infty)\) alcance e assíntota vertical,\(x=0\), que não são alterados em relação à função principal.
A função\(f(x)={\log}_b(−x)\)
- reflete a função principal\(y={\log}_b(x)\) sobre o\(y\) eixo y.
- tem domínio\((−\infty,0)\).
- tem alcance,\((−\infty,\infty)\), e assíntota vertical\(x=0\), que não são alterados em relação à função principal.
| E se\(f(x)=−{\log}_b(x)\) | E se\(f(x)={\log}_b(−x)\) |
|---|---|
\ (f (x) =− {\ log} _b (x)\) ">
|
\ (f (x) = {\ log} _b (−x)\) ">
|
\ (f (x) =− {\ log} _b (x)\) ">
|
\ (f (x) = {\ log} _b (−x)\) ">
|
\ (f (x) =− {\ log} _b (x)\) ">
|
\ (f (x) = {\ log} _b (−x)\) ">
|
\ (f (x) =− {\ log} _b (x)\) ">
|
\ (f (x) = {\ log} _b (−x)\) ">
|
\ (f (x) =− {\ log} _b (x)\) ">
|
\ (f (x) = {\ log} _b (−x)\) ">
|
Esboce um gráfico\(f(x)=\log(−x)\) ao lado de sua função principal. Inclua os pontos-chave e a assíntota no gráfico. Indique o domínio, o alcance e a assíntota.
Solução
Antes de representar graficamente\(f(x)=log(−x)\)\(f(x)=log(−x)\), identifique o comportamento e os pontos-chave do gráfico.
- Como\(b=10\) é maior que um, sabemos que a função principal está aumentando. Como o valor de entrada é multiplicado por\(−1\),\(f(x)\) é um reflexo do gráfico principal sobre o eixo\(y\) -. Assim,\(f(x)=\log(−x)\) diminuirá à medida que\(x\) se move do infinito negativo para zero, e a cauda direita do gráfico se aproximará da assíntota vertical\(x=0\).
- O\(x\) intercepto -é\((−1,0)\).
- Desenhamos e rotulamos a assíntota, traçamos e rotulamos os pontos e desenhamos uma curva suave através dos pontos.
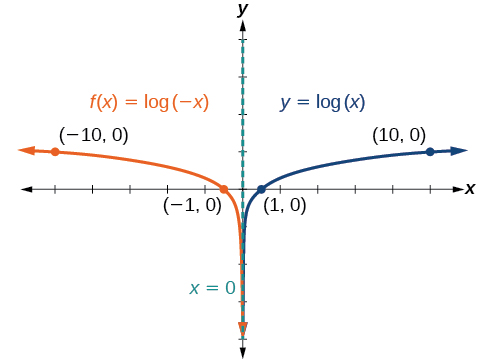
O domínio é\((−\infty,0)\), o intervalo é\((−\infty,\infty)\) e a assíntota vertical é\(x=0\).
Gráfico\(f(x)=−\log(−x)\). Indique o domínio, o alcance e a assíntota.
- Responda
-
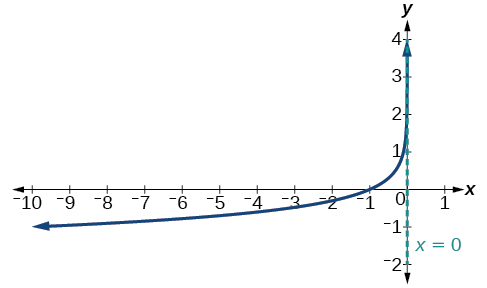
Figura\(\PageIndex{20}\) O domínio é\((−\infty,0)\), o intervalo é\((−\infty,\infty)\) e a assíntota vertical é\(x=0\).
- Pressione [Y=]. Insira a equação ou equações logarítmicas fornecidas como Y 1 = e, se necessário, Y 2 =.
- Pressione [GRÁFICO] para observar os gráficos das curvas e use [JANELA] para encontrar uma visualização apropriada dos gráficos, incluindo seus pontos de interseção.
- Para encontrar o valor de\(x\), calculamos o ponto de interseção. Pressione [2ND] e depois [CALC]. Selecione “intersect” e pressione [ENTER] três vezes. O ponto de interseção fornece o valor de\(x\), para o (s) ponto (s) de interseção.
Resolva\(4\ln(x)+1=−2\ln(x−1)\) graficamente. Arredonde para o milésimo mais próximo.
Solução
Pressione [Y=] e digite\(4\ln(x)+1\) ao lado de Y 1 =. Em seguida, digite ao\(−2\ln(x−1)\) lado de Y 2 =. Para uma janela, use os valores\(0\) de\(5\) para\(x\0 and \(–10\) para\(10\) para\(y\). Pressione [GRAPH]. Os gráficos devem se cruzar em algum lugar um pouco à direita\(x=1\).
Para uma melhor aproximação, pressione [2ND] e depois [CALC]. Selecione [5: interseção] e pressione [ENTER] três vezes. A coordenada x do ponto de interseção é exibida como\(1.3385297\). (Sua resposta pode ser diferente se você usar uma janela diferente ou usar um valor diferente para Guess? ) Então, até o milésimo mais próximo,\(x≈1.339\).
Resolva\(5\log(x+2)=4−\log(x)\) graficamente. Arredonde para o milésimo mais próximo.
- Responda
-
\(x≈3.049\)
Resumindo traduções da função logarítmica
Agora que trabalhamos com cada tipo de tradução para a função logarítmica, podemos resumir cada uma na Tabela\(\PageIndex{4}\) para chegar à equação geral para traduzir funções exponenciais.
| Traduções da função parental\(y={\log}_b(x)\) | |
|---|---|
| Tradução | Formulário |
| \ (y= {\ log} _b (x)\) Tradução">
Mudar \(c\)Unidades horizontalmente à esquerda \(d\)Unidades verticalmente para cima |
\ (y= {\ log} _b (x)\) Forma” style="vertical-align:middle; ">\(y={\log}_b(x+c)+d\) |
| \ (y= {\ log} _b (x)\) Tradução">
Estique e comprima Estique se\(|a|>1\) Compressão se\(|a|<1\) |
\ (y= {\ log} _b (x)\) Forma” style="vertical-align:middle; ">\(y=a{\log}_b(x)\) |
| \ (y= {\ log} _b (x)\) Tradução">Reflita sobre o eixo x | \ (y= {\ log} _b (x)\) Formulário">\(y=−{\log}_b(x)\) |
| \ (y= {\ log} _b (x)\) Tradução">Reflita sobre o eixo y | \ (y= {\ log} _b (x)\) Formulário">\(y={\log}_b(−x)\) |
| \ (y= {\ log} _b (x)\) Tradução">Equação geral para todas as traduções | \ (y= {\ log} _b (x)\) Formulário">\(y=a{\log}_b(x+c)+d\) |
Todas as traduções da função logarítmica principal,\(y={\log}_b(x)\), têm a forma
\(f(x)=a{\log}_b(x+c)+d\)
onde a função principal,\(y={\log}_b(x)\),\(b>1\), é
- \(d\)unidades deslocadas verticalmente para cima.
- deslocado horizontalmente para as\(c\) unidades esquerdas.
- esticado verticalmente por um fator de\(|a|\) if\(|a|>0\).
- comprimido verticalmente por um fator de\(|a|\) if\(0<|a|<1\).
- refletido sobre o eixo x quando\(a<0\).
Pois\(f(x)=\log(−x)\), o gráfico da função principal é refletido sobre o eixo y.
Do que é a assíntota vertical de\(f(x)=−2{\log}_3(x+4)+5\)?
Solução
A assíntota vertical está em\(x=−4\).
Análise
O coeficiente, a base e a translação ascendente não afetam a assíntota. O deslocamento das\(4\) unidades da curva para a esquerda desloca a assíntota vertical para\(x=−4\).
Do que é a assíntota vertical de\(f(x)=3+\ln(x−1)\)?
- Responda
-
\(x=1\)
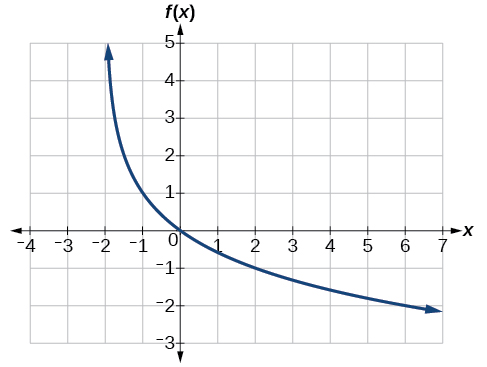
Encontre uma equação possível para a função logarítmica comum representada graficamente na Figura\(\PageIndex{21}\).
Solução
Este gráfico tem uma assíntota vertical em\(x=–2\) e foi refletido verticalmente. Ainda não sabemos o deslocamento vertical ou o alongamento vertical. Sabemos até agora que a equação terá forma:
\(f(x)=−a\log(x+2)+k\)
Parece que o gráfico passa pelos pontos\((–1,1)\)\((2,–1)\) e. Substituindo\((–1,1)\),
\[\begin{align*} 1&= -a\log(-1+2)+k \qquad \text{Substitute} (-1,1)\\ 1&= -a\log(1)+k \qquad \text{Arithmetic}\\ 1&= k\log(1)\\ &= 0 \end{align*}\]
Em seguida, substituindo em\((2,–1)\),
\[\begin{align*} -1&= -a\log(2+2)+1 \qquad \text{Substitute} (2,-1)\\ -2&= -a\log(4) \qquad \text{Arithmetic}\\ a&= \dfrac{2}{\log(4)} \qquad \text{Solve for a} \end{align*}\]
Isso nos dá a equação\(f(x)=–\dfrac{2}{\log(4)}\log(x+2)+1\).
Análise
Podemos verificar essa resposta comparando os valores da função na Tabela\(\PageIndex{5}\) com os pontos no gráfico na Figura\(\PageIndex{21}\).
| \(x\) | −1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|
| \(f(x)\) | 1 | 0 | −0,58496 | −1 | −1,3219 |
| \(x\) | 4 | 5 | 6 | 7 | 8 |
| \(f(x)\) | −1,5850 | −1,8074 | −2 | −2.169 | −2,3219 |
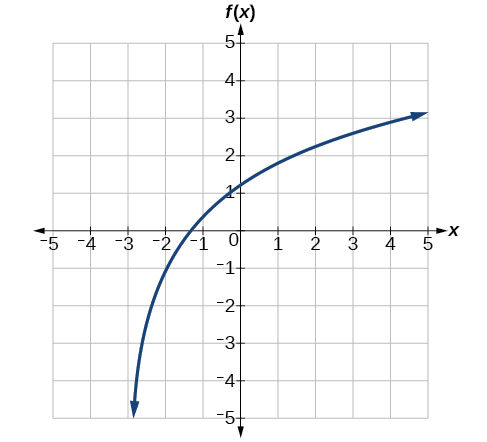
Dê a equação do logaritmo natural representado graficamente na Figura\(\PageIndex{22}\).
- Responda
-
\(f(x)=2\ln(x+3)−1\)
Sim, se soubermos que a função é uma função logarítmica geral. Por exemplo, veja o gráfico na Figura\(\PageIndex{22}\). O gráfico se aproxima\(x=−3\) (ou por aí) cada vez mais de perto, assim como\(x=−3\) é, ou está muito próximo, da assíntota vertical. Ele se aproxima pela direita, então o domínio está todo apontado para a direita,\({x|x>−3}\). O intervalo, como em todas as funções logarítmicas gerais, são todos números reais. E podemos ver o comportamento final porque o gráfico desce à medida que vai para a esquerda e para cima à medida que vai para a direita. O comportamento final é aquele como\(x\rightarrow −3^+\),\(f(x)\rightarrow −\infty\) e como\(x\rightarrow \infty\),\(f(x)\rightarrow \infty\).
Acesse esses recursos on-line para obter instruções e práticas adicionais com gráficos de logaritmos.
- Representar graficamente uma função exponencial e uma função logarítmica
- Combine gráficos com funções exponenciais e logarítmicas
- Encontre o domínio das funções logarítmicas
Equações-chave
| Formulário geral para a tradução da função logarítmica principal\(f(x)={\log}_b(x)\) | \(f(x)=a{\log}_b(x+c)+d\) |
Conceitos-chave
- Para encontrar o domínio de uma função logarítmica, configure uma desigualdade mostrando o argumento maior que zero e resolva para\(x\). Veja o exemplo\(\PageIndex{1}\) e o exemplo\(\PageIndex{2}\)
- O gráfico da função principal\(f(x)={\log}_b(x)\) tem um intercepto x em\((1,0)\), domínio\((0,\infty)\), alcance\((−\infty,\infty)\), assíntota\(x=0\) vertical e
-
- se\(b>1\), a função está aumentando.
- se\(0<b<1\), a função está diminuindo.
- A equação\(f(x)={\log}_b(x+c)\) desloca a função principal\(y={\log}_b(x)\) horizontalmente
- \(c\)unidades esquerdas se\(c>0\).
- \(c\)unidades certas se\(c<0\).
- A equação\(f(x)={\log}_b(x)+d\) desloca a função principal\(y={\log}_b(x)\) verticalmente
- até\(d\) unidades se\(d>0\).
- \(d\)unidades inativas se\(d<0\).
- Para qualquer constante\(a>0\), a equação\(f(x)=a{\log}_b(x)\)
- alonga a função principal\(y={\log}_b(x)\) verticalmente por um fator de\(a\) if\(|a|>1\).
- comprime a função principal\(y={\log}_b(x)\) verticalmente por um fator de\(a\) if\(|a|<\) 1.
- Quando a função principal\(y={\log}_b(x)\) é multiplicada por\(−1\), o resultado é uma reflexão sobre o eixo x. Quando a entrada é multiplicada por\(−1\), o resultado é uma reflexão sobre o eixo y.
- A equação\(f(x)=−{\log}_b(x)\) representa um reflexo da função principal sobre o eixo x.
- A equação\(f(x)={\log}_b(−x)\) representa um reflexo da função principal sobre o eixo y.
- Uma calculadora gráfica pode ser usada para aproximar soluções para algumas equações logarítmicas. Veja o exemplo\(\PageIndex{9}\).
- Todas as traduções da função logarítmica podem ser resumidas pela equação geral\(f(x)=a{\log}_b(x+c)+d\). Veja a tabela\(\PageIndex{4}\).
- Dada uma equação com a forma geral\(f(x)=a{\log}_b(x+c)+d\), podemos identificar a assíntota vertical\(x=−c\) para a transformação. Veja o exemplo\(\PageIndex{10}\).
- Usando a equação geral\(f(x)=a{\log}_b(x+c)+d\), podemos escrever a equação de uma função logarítmica dado seu gráfico. Veja o exemplo\(\PageIndex{11}\).


