4.3: Funções logarítmicas
- Page ID
- 189223
- Converta da forma logarítmica para exponencial.
- Converta da forma exponencial para a forma logarítmica.
- Avalie logaritmos.
- Use logaritmos comuns.
- Use logaritmos naturais.
Em 2010, um grande terremoto atingiu o Haiti, destruindo ou danificando mais de 285.000 casas. Um ano depois, outro terremoto mais forte devastou Honshu, Japão, destruindo ou danificando mais de 332.000 edifícios, como os mostrados na Figura\(\PageIndex{1}\). Embora ambos tenham causado danos substanciais, o terremoto de 2011 foi 100 vezes mais forte do que o terremoto no Haiti. Como sabemos? As magnitudes dos terremotos são medidas em uma escala conhecida como Escala Richter. O terremoto haitiano registrou 7,0 na escala Richter, enquanto o terremoto japonês registrou 9,0.

Figura\(\PageIndex{1}\): Devastação do terremoto de 11 de março de 2011 em Honshu, Japão. (crédito: Daniel Pierce).
A Escala Richter é uma escala logarítmica de base dez. Em outras palavras, um terremoto de magnitude não\(8\) é duas vezes maior que um terremoto de magnitude\(4\). É
\[10^{8−4}=10^4=10,000 \nonumber\]
vezes tão boas! Nesta lição, investigaremos a natureza da Escala Richter e a função de base dez da qual ela depende.
Conversão da forma logarítmica para exponencial
Para analisar a magnitude dos terremotos ou comparar as magnitudes de dois terremotos diferentes, precisamos ser capazes de converter entre a forma logarítmica e exponencial. Por exemplo, suponha que a quantidade de energia liberada de um terremoto seja 500 vezes maior do que a quantidade de energia liberada de outro. Queremos calcular a diferença de magnitude. A equação que representa esse problema é\(10^x=500\), onde\(x\) representa a diferença de magnitudes na Escala Richter. Como resolveríamos isso\(x\)?
Ainda não aprendemos um método para resolver equações exponenciais. Nenhuma das ferramentas algébricas discutidas até agora é suficiente para resolver\(10^x=500\). Sabemos disso\({10}^2=100\) e\({10}^3=1000\), portanto, está claro que\(x\) deve haver algum valor entre 2 e 3, pois\(y={10}^x\) está aumentando. Podemos examinar um gráfico, como na Figura\(\PageIndex{1}\), para estimar melhor a solução.
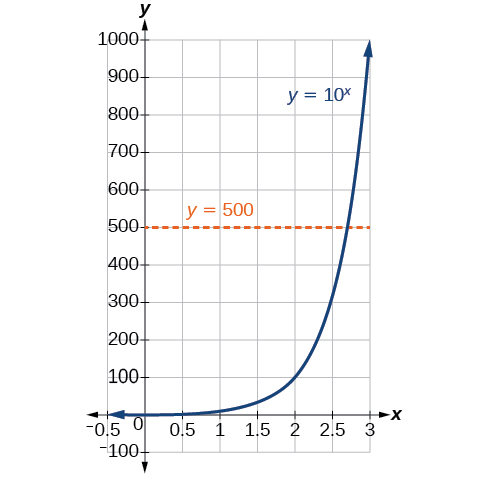
Figura\(\PageIndex{2}\)
A estimativa a partir de um gráfico, no entanto, é imprecisa. Para encontrar uma solução algébrica, devemos introduzir uma nova função. Observe que o gráfico na Figura\(\PageIndex{2}\) passa no teste da linha horizontal. A função exponencial\(y=b^x\) é de um para um, então seu inverso também\(x=b^y\) é uma função. Como é o caso de todas as funções inversas, simplesmente trocamos\(x\)\(y\) e resolvemos\(y\) para encontrar a função inversa. Para representar\(y\) como uma função de\(x\), usamos uma função logarítmica do formulário\(y={\log}_b(x)\). O\(b\) logaritmo base de um número é o expoente pelo qual devemos aumentar\(b\) para obter esse número.
Lemos uma expressão logarítmica como: “O logaritmo com base\(b\) de\(x\) é igual a” ou\(y\), simplificado, “logarítmico\(b\) de\(x\) é”\(y\). Também podemos dizer “\(b\)elevado à potência de\(y\) é”\(x\), porque os registros são expoentes. Por exemplo, o\(2\) logaritmo base de\(32\) é\(5\), porque\(5\) é o expoente ao qual devemos aplicar\(2\) para obter\(32\). Desde então\(2^5=32\), podemos escrever\({\log}_232=5\). Lemos isso como “base\(2\) logarítmica de\(32\) is”\(5\).
Podemos expressar a relação entre a forma logarítmica e sua forma exponencial correspondente da seguinte forma:
\[\begin{align} \log_b(x)=y\Leftrightarrow b^y=x, b> 0, b\neq 1 \end{align}\]
Note que a base\(b\) é sempre positiva.
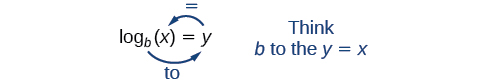
Como o logaritmo é uma função, ele é escrito corretamente como\(\log_b(x)\), usando parênteses para denotar a avaliação da função, assim como faríamos com\(f(x)\). No entanto, quando a entrada é uma única variável ou número, é comum ver os parênteses eliminados e a expressão escrita sem parênteses, como\(\log_bx\). Observe que muitas calculadoras exigem parênteses ao redor do\(x\).
Podemos ilustrar a notação dos logaritmos da seguinte forma:

Observe que, comparando a função logarítmica e a função exponencial, a entrada e a saída são comutadas. Isso significa\(y={\log}^b(x)\) e\(y=b^x\) são funções inversas.
A base logarítmica\(b\) de um número positivo\(x\) satisfaz a seguinte definição.
Para\(x>0\),\(b>0\),\(b≠1\),
\[\begin{align} y={\log}_b(x)\text{ is equivalent to } b^y=x \end{align}\]
onde,
- lemos\({\log}_b(x)\) como “o logaritmo com base\(b\) de\(x\)” ou a “base logarítmica\(b\) de”\(x\).
- o logaritmo\(y\) é o expoente ao qual\(b\) deve ser aumentado para obter\(x\).
Além disso, como as funções logarítmica e exponencial alternam\(y\) os valores\(x\) e, o domínio e o alcance da função exponencial são trocados pela função logarítmica. Portanto,
- o domínio da função logarítmica com base\(b\) é\((0,\infty)\).
- o intervalo da função logarítmica com base\(b\) é\((−\infty,\infty)\).
Não. Como a base de uma função exponencial é sempre positiva, nenhuma potência dessa base pode ser negativa. Nunca podemos usar o logaritmo de um número negativo. Além disso, não podemos usar o logaritmo de zero. As calculadoras podem gerar um log de um número negativo no modo complexo, mas o log de um número negativo não é um número real.
- Examine a equação\(y={\log}_bx\) e identifique\(b\)\(y\),\(x\) e.
- Reescreva\({\log}_bx=y\) como\(b^y=x\).
Escreva as seguintes equações logarítmicas na forma exponencial.
- \({\log}_6(\sqrt{6})=\dfrac{1}{2}\)
- \({\log}_3(9)=2\)
Solução
Primeiro, identifique os valores de\(b\)\(y\),\(x\) e. Em seguida, escreva a equação no formulário\(b^y=x\).
- \({\log}_6(\sqrt{6})=\dfrac{1}{2}\)
Aqui\(b=6\),\(y=\dfrac{1}{2}\),\(x=\sqrt{6}\) e. Portanto, a equação\({\log}_6(\sqrt{6})=\dfrac{1}{2}\) é equivalente a
\(6^{\tfrac{1}{2}}=\sqrt{6}\)
- \({\log}_3(9)=2\)
Aqui\(b=3\),\(y=2\),\(x=9\) e. Portanto, a equação\({\log}_3(9)=2\) é equivalente a
\(3^2=9\)
Escreva as seguintes equações logarítmicas na forma exponencial.
- \({\log}_{10}(1,000,000)=6\)
- \({\log}_5(25)=2\)
- Responda a
-
\({\log}_{10}(1,000,000)=6\)é equivalente a\({10}^6=1,000,000\)
- Resposta b
-
\({\log}_5(25)=2\)é equivalente a\(5^2=25\)
Conversão da forma exponencial para a forma logarítmica
Para converter de expoentes em logaritmos, seguimos os mesmos passos ao contrário. Identificamos a base\(b\), o expoente\(x\) e a saída\(y\). Em seguida, escrevemos\(x={\log}_b(y)\).
Escreva as seguintes equações exponenciais na forma logarítmica.
- \(2^3=8\)
- \(5^2=25\)
- \({10}^{−4}=\dfrac{1}{10,000}\)
Solução
Primeiro, identifique os valores de\(b\)\(y\),\(x\) e. Em seguida, escreva a equação no formulário\(x={\log}_b(y)\).
- \(2^3=8\)
Aqui\(b=2\),\(x=3\),\(y=8\) e. Portanto, a equação\(2^3=8\) é equivalente\({\log}_2(8)=3\) a.
- \(5^2=25\)
Aqui\(b=5\),\(x=2\),\(y=25\) e. Portanto, a equação\(5^2=25\) é equivalente\({\log}_5(25)=2\) a.
- \({10}^{−4}=\dfrac{1}{10,000}\)
Aqui\(b=10\),\(x=−4\),\(y=\dfrac{1}{10,000}\) e. Portanto, a equação\({10}^{−4}=\dfrac{1}{10,000}\) é equivalente\({\log}_{10} \left (\dfrac{1}{10,000} \right )=−4\) a.
Escreva as seguintes equações exponenciais na forma logarítmica.
- \(3^2=9\)
- \(5^3=125\)
- \(2^{−1}=\dfrac{1}{2}\)
- Responda a
-
\(3^2=9\)é equivalente a\({\log}_3(9)=2\)
- Resposta b
-
\(5^3=125\)é equivalente a\({\log}_5(125)=3\)
- Resposta c
-
\(2^{−1}=\dfrac{1}{2}\)é equivalente a\({\log}_2 \left (\dfrac{1}{2} \right )=−1\)
Cálculo de logaritmos
Conhecer os quadrados, cubos e raízes dos números nos permite avaliar muitos logaritmos mentalmente. Por exemplo, considere\({\log}_28\). Perguntamos: “Para qual expoente deve\(2\) ser elevado para obter 8?” Porque já sabemos\(2^3=8\), segue isso\({\log}_28=3\).
Agora, considere resolver\({\log}_749\) e\({\log}_327\) mentalmente.
- Perguntamos: “Para qual expoente deve\(7\) ser elevado para chegar\(49\)?” Nós sabemos\(7^2=49\). Portanto,\({\log}_749=2\)
- Perguntamos: “Para qual expoente deve\(3\) ser elevado para chegar\(27\)?” Nós sabemos\(3^3=27\). Portanto,\(\log_{3}27=3\)
Até mesmo alguns logaritmos aparentemente mais complicados podem ser avaliados sem uma calculadora. Por exemplo, vamos avaliar\(\log_{\ce{2/3}} \frac{4}{9}\) mentalmente.
- Perguntamos: “Para qual expoente deve\(\ce{2/3}\) ser elevado para chegar\(\ce{4/9}\)? ” Nós sabemos\(2^2=4\) e\(3^2=9\),\[{\left(\dfrac{2}{3} \right )}^2=\dfrac{4}{9}. \nonumber\] portanto,\[{\log}_{\ce{2/3}} \left (\dfrac{4}{9} \right )=2. \nonumber\]
- Reescreva o argumento\(x\) como um poder de\(b\):\(b^y=x\).
- Use o conhecimento prévio dos poderes de\(b\) identificação\(y\) perguntando: “Para qual expoente deve\(b\) ser elevado para chegar\(x\)?”
Resolva\(y={\log}_4(64)\) sem usar uma calculadora.
Solução
Primeiro, reescrevemos o logaritmo na forma exponencial:\(4^y=64\). Em seguida, perguntamos: “Para qual expoente deve\(4\) ser elevado para chegar\(64\)?”
Nós sabemos
\(4^3=64\)
Portanto,
\({\log}_4(64)=3\)
Resolva\(y={\log}_{121}(11)\) sem usar uma calculadora.
- Responda
-
\({\log}_{121}(11)=\dfrac{1}{2}\)(lembrando que\(\sqrt{121}={(121)}^{\tfrac{1}{2}}=11)\)
Avalie\(y={\log}_3 \left (\dfrac{1}{27} \right )\) sem usar uma calculadora.
Solução
Primeiro, reescrevemos o logaritmo na forma exponencial:\(3^y=\dfrac{1}{27}\). Em seguida, perguntamos: “Para qual expoente deve\(3\) ser elevado para chegar\(\dfrac{1}{27}\)?”
Nós sabemos\(3^3=27\), mas o que devemos fazer para obter o recíproco,\(\dfrac{1}{27}\)? Lembre-se de trabalhar com expoentes que\(b^{−a}=\dfrac{1}{b^a}\). Usamos essas informações para escrever
\[\begin{align*} 3^{-3}&= \dfrac{1}{3^3}\\ &= \dfrac{1}{27} \end{align*}\]
Portanto,\({\log}_3 \left (\dfrac{1}{27} \right )=−3\).
Avalie\(y={\log}_2 \left (\dfrac{1}{32} \right )\) sem usar uma calculadora.
- Responda
-
\({\log}_2 \left (\dfrac{1}{32} \right )=−5\)
Usando logaritmos comuns
Às vezes, podemos ver um logaritmo escrito sem uma base. Nesse caso, assumimos que a base é\(10\). Em outras palavras, a expressão\(\log(x)\) significa\({\log}_{10}(x)\). Chamamos um\(-10\) logaritmo base de logaritmo comum. Logaritmos comuns são usados para medir a Escala Richter mencionada no início da seção. As escalas para medir o brilho das estrelas e o pH dos ácidos e bases também usam logaritmos comuns.
Um logaritmo comum é um logaritmo com base\(10\). Nós escrevemos\({\log}_{10}(x)\) simplesmente como\(\log(x)\). O logaritmo comum de um número positivo\(x\) satisfaz a seguinte definição.
Para\(x>0\),
\[\begin{align} y={\log}(x)\text{ is equivalent to } {10}^y=x \end{align}\]
Lemos\(\log(x)\) como “o logaritmo com base\(10\) de\(x\)” ou “logaritmo com base\(10\) de”\(x\).
O logaritmo\(y\) é o expoente ao qual\(10\) deve ser aumentado para obter\(x\).
- Reescreva o argumento\(x\) como um poder de\(10\):\({10}^y=x\).
- Use o conhecimento prévio dos poderes de\(10\) para identificar\(y\) perguntando: “Para qual expoente deve\(10\) ser elevado para chegar\(x\)?”
Avalie\(y=\log(1000)\) sem usar uma calculadora.
Solução
Primeiro, reescrevemos o logaritmo na forma exponencial:\({10}^y=1000\). Em seguida, perguntamos: “Para qual expoente deve\(10\) ser elevado para chegar\(1000\)?” Nós sabemos
\({10}^3=1000\)
Portanto,\(\log(1000)=3\).
Avalie\(y=\log(1,000,000)\).
- Responda
-
\(\log(1,000,000)=6\)
- Pressione [LOG].
- Insira o valor fornecido para\(x\), seguido por [)].
- Pressione [ENTER].
Avalie\(y=\log(321)\) até quatro casas decimais usando uma calculadora.
Solução
- Pressione [LOG].
- Insira 321, seguido por [)].
- Pressione [ENTER].
Arredondando para quatro casas decimais,\(\log(321)≈2.5065\).
Análise
Observe isso\({10}^2=100\) e aquilo\({10}^3=1000\). Uma vez que\(321\) está entre\(100\) e\(1000\), sabemos que\(\log(321)\) deve ser entre\(\log(100)\)\(\log(1000)\) e. Isso nos dá o seguinte:
\(100<321<1000\)
\(2<2.5065<3\)
Avalie\(y=\log(123)\) até quatro casas decimais usando uma calculadora.
- Responda
-
\(\log(123)≈2.0899\)
A quantidade de energia liberada de um terremoto foi\(500\) vezes maior do que a quantidade de energia liberada de outro. A equação\({10}^x=500\) representa essa situação, onde\(x\) está a diferença de magnitudes na Escala Richter. Até o milésimo mais próximo, qual foi a diferença nas magnitudes?
Solução
Começamos reescrevendo a equação exponencial na forma logarítmica.
\({10}^x=500\)
\(\log(500)=x\)Use a definição do registro comum.
Em seguida, avaliamos o logaritmo usando uma calculadora:
- Pressione [LOG].
- Digite\(500\), seguido por [)].
- Pressione [ENTER].
- Até o milésimo mais próximo,\(\log(500)≈2.699\).
A diferença nas magnitudes era de cerca de\(2.699\).
A quantidade de energia liberada de um terremoto foi\(8,500\) vezes maior do que a quantidade de energia liberada de outro. A equação\({10}^x=8500\) representa essa situação, onde\(x\) está a diferença de magnitudes na Escala Richter. Até o milésimo mais próximo, qual foi a diferença nas magnitudes?
- Responda
-
A diferença nas magnitudes era de cerca de\(3.929\).
Usando logaritmos naturais
A base usada com mais frequência para logaritmos é\(e\). Os\(e\) logaritmos de base são importantes no cálculo e em algumas aplicações científicas; eles são chamados de logaritmos naturais. O\(e\) logaritmo base\({\log}_e(x)\),, tem sua própria notação,\(\ln(x)\). A maioria dos valores de só\(\ln(x)\) pode ser encontrada usando uma calculadora. A principal exceção é que, porque o logaritmo de\(1\) está sempre\(0\) em qualquer base,\(\ln1=0\). Para outros logaritmos naturais, podemos usar a\(\ln\) chave que pode ser encontrada na maioria das calculadoras científicas. Também podemos encontrar o logaritmo natural de qualquer potência de\(e\) usar a propriedade inversa dos logaritmos.
Um logaritmo natural é um logaritmo com base\(e\). Nós escrevemos\({\log}_e(x)\) simplesmente como\(\ln(x)\). O logaritmo natural de um número positivo\(x\) satisfaz a seguinte definição.
Para\(x>0\),
\(y=\ln(x)\)é equivalente a\(e^y=x\)
Lemos\(\ln(x)\) como “o logaritmo com base\(e\) de\(x\)” ou “o logaritmo natural de”\(x\).
O logaritmo\(y\) é o expoente ao qual\(e\) deve ser aumentado para obter\(x\).
Uma vez que as funções\(y=e^x\) e\(y=\ln(x)\) são funções inversas,\(\ln(e^x)=x\) para todos\(x\) e\(e^{\ln (x)}=x\) para\(x>0\).
- Pressione [LN].
- Insira o valor fornecido para\(x\), seguido por [)].
- Pressione [ENTER].
Avalie\(y=\ln(500)\) até quatro casas decimais usando uma calculadora.
Solução
- Pressione [LN].
- Digite\(500\), seguido por [)].
- Pressione [ENTER].
Arredondando para quatro casas decimais,\(\ln(500)≈6.2146\)
Avalie\(\ln(−500)\).
- Responda
-
Não é possível obter o logaritmo de um número negativo no conjunto dos números reais.
Acesse esse recurso on-line para obter instruções e práticas adicionais com logaritmos.
Equações-chave
| Definição da função logarítmica | Para\(x>0\),\(b>0\)\(b≠1\),\(y={\log}_b(x)\) se e somente se\(b^y=x\). |
| Definição do logaritmo comum | Para\(x>0\),\(y=\log(x)\) se e somente se\({10}^y=x\). |
| Definição do logaritmo natural | Para\(x>0\),\(y=\ln(x)\) se e somente se\(e^y=x\). |
Conceitos-chave
- O inverso de uma função exponencial é uma função logarítmica e o inverso de uma função logarítmica é uma função exponencial.
- As equações logarítmicas podem ser escritas em uma forma exponencial equivalente, usando a definição de um logaritmo. Veja o exemplo\(\PageIndex{1}\).
- As equações exponenciais podem ser escritas em sua forma logarítmica equivalente usando a definição de um logaritmo. Veja o exemplo\(\PageIndex{2}\).
- As funções logarítmicas com base\(b\) podem ser avaliadas mentalmente usando o conhecimento prévio dos poderes de\(b\). Veja o exemplo\(\PageIndex{3}\) e o exemplo\(\PageIndex{4}\).
- Os logaritmos comuns podem ser avaliados mentalmente usando o conhecimento prévio dos poderes de\(10\). Veja o exemplo\(\PageIndex{5}\).
- Quando logaritmos comuns não podem ser avaliados mentalmente, uma calculadora pode ser usada. Veja o exemplo\(\PageIndex{6}\).
- Problemas exponenciais do mundo real com base\(10\) podem ser reescritos como um logaritmo comum e depois avaliados usando uma calculadora. Veja o exemplo\(\PageIndex{7}\).
- Os logaritmos naturais podem ser avaliados usando um exemplo de calculadora\(\PageIndex{8}\).


