3.E: Funções polinomiais e racionais (exercícios)

3.1 Números complexos

Verbal

1) Explique como adicionar números complexos.

Resposta

Adicione as partes reais e as partes imaginárias.

2) Qual é o princípio básico na multiplicação de números complexos?

3) Dê um exemplo para mostrar que o produto de dois números imaginários nem sempre é imaginário.

Resposta

\(i\)vezes\(i\) iguais\(-1\), o que não é imaginário (as respostas variam)

4) Qual é a característica do gráfico de um número real no plano complexo?

Algébrico

Para os exercícios 5-10, avalie as expressões algébricas.

5) Se\(f(x)=x^2+x−4\), avalie\(f(2i)\).

Resposta

\(−8+2i\)

6) Se\(f(x)=x^3−2\), avalie\(f(i)\).

7) Se\(f(x)=x^2+3x+5\), avalie\(f(2+i)\).

Resposta

\(14+7i\)

8) Se\(f(x)=2x^2+x−3\), avalie\(f(2−3i)\).

9) Se\(f(x)=\dfrac{x+1}{2−x}\), avalie\(f(5i)\).

Resposta

\(−\dfrac{23}{29}+\dfrac{15}{29}i\)

10) Se\(f(x)=\dfrac{1+2x}{x+3}\), avalie\(f(4i)\).

Gráfica

Para os exercícios 11-12, determine o número de soluções reais e não reais para cada função quadrática mostrada.

11)

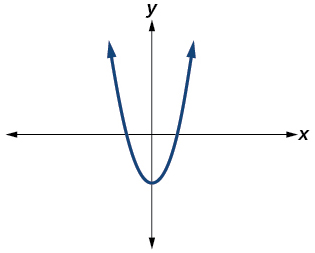
Responda

\(2\)real e\(0\) não real

12)

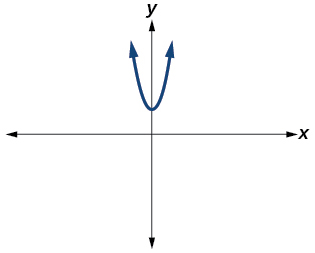
Para os exercícios 13-16, plote os números complexos no plano complexo.

13)\(1−2i\)

Responda

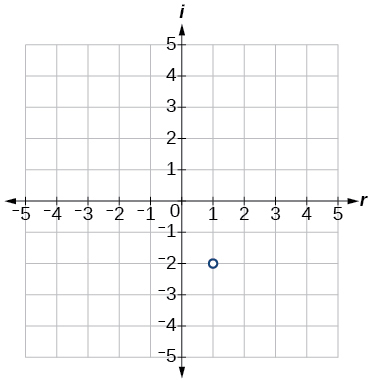
14)\(−2+3i\)

15)\(i\)

Responda

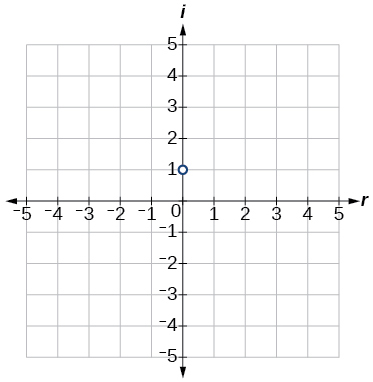
16)\(−3−4i\)

Numérico

Para os exercícios 17-43, execute a operação indicada e expresse o resultado como um número complexo simplificado.

17)\((3+2i)+(5−3i)\)

Responda

\(8−i\)

18)\((−2−4i)+(1+6i)\)

19)\((−5+3i)−(6−i)\)

Responda

\(−11+4i\)

20)\((2−3i)−(3+2i)\)

21)\((−4+4i)−(−6+9i)\)

Responda

\(2−5i\)

22)\((2+3i)(4i)\)

23)\((5−2i)(3i)\)

Responda

\(6+15i\)

24)\((6−2i)(5)\)

25)\((−2+4i)(8)\)

Responda

\(−16+32i\)

26)\((2+3i)(4−i)\)

27)\((−1+2i)(−2+3i)\)

Responda

\(−4−7i\)

28)\((4−2i)(4+2i)\)

29)\((3+4i)(3−4i)\)

Responda

\(25\)

30)\(\dfrac{3+4i}{2}\)

31)\(\dfrac{6−2i}{3}\)

Responda

\(2−\dfrac{2}{3}i\)

32)\(\dfrac{−5+3i}{2i}\)

33)\(\dfrac{6+4i}{i}\)

Responda

\(4−6i\)

34)\(\dfrac{2−3i}{4+3i}\)

(35)\(\dfrac{3+4i}{2−i}\)

Responda

\(\dfrac{2}{5}+\dfrac{11}{5}i\)

36)\(\dfrac{2+3i}{2−3i}\)

37)\(\sqrt{−9}+3\sqrt{−16}\)

Responda

\(15i\)

38)\(−\sqrt{−4}−4\sqrt{−25}\)

39)\(\dfrac{2+\sqrt{−12}}{2}\)

Responda

\(1+i\sqrt{3}\)

40)\(\dfrac{4+\sqrt{−20}}{2}\)

41)\(i^8\)

Responda

\(1\)

(42)\(i^{15}\)

43)\(i^{22}\)

Responda

\(−1\)

Tecnologia

Para os exercícios 44-48, use uma calculadora para ajudar a responder às perguntas.

44) Avalie\((1+i)^k\) para\(k=4, 8, \) e\(12\) .Preveja o valor se\(k=16\).

45) Avalie\((1−i)^k\) para\(k=2, 6,\) e\(10\) .Preveja o valor se\(k=14\).

Responda

\(128i\)

46) Avalie\((1+i)^k-(1-i)^k\) para\(k=4\)\(8\),\(12\) e. Preveja o valor de\(k=16\).

47) Mostre que uma solução de\(x^6+1=0\) é\(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i\).

Responda

\((\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i)^6=−1\)

48) Mostre que uma solução de\(x^8−1=0\) é\(\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2}i\).

Extensões

Para os exercícios 49-58, avalie as expressões, escrevendo o resultado como um número complexo simplificado.

49)\(\dfrac{1}{i}+\dfrac{4}{i^3}\)

Responda

\(3i\)

50)\(\dfrac{1}{i^{11}}−\dfrac{1}{i^{21}}\)

51)\(i^7(1+i^2)\)

Responda

\(0\)

52)\(i^{−3}+5i^7\)

53)\(\dfrac{(2+i)(4−2i)}{(1+i)}\)

Responda

\(5 – 5i\)

54)\(\dfrac{(1+3i)(2−4i)}{(1+2i)}\)

55)\(\dfrac{(3+i)^2}{(1+2i)^2}\)

Responda

\(−2i\)

56)\(\dfrac{3+2i}{2+i}+(4+3i)\)

57)\(\dfrac{4+i}{i}+\dfrac{3−4i}{1−i}\)

Responda

\(\dfrac{9}{2}−\dfrac{9}{2}i\)

(58)\(\dfrac{3+2i}{1+2i}−\dfrac{2−3i}{3+i}\)

3.2 Funções quadráticas

Verbal

1) Explique a vantagem de escrever uma função quadrática na forma padrão.

Responda

Quando escrito dessa forma, o vértice pode ser facilmente identificado.

2) Como o vértice de uma parábola pode ser usado na solução de problemas do mundo real?

3) Explique por que a condição de\(a≠0\) é imposta na definição da função quadrática.

Responda

Se\(a=0\) então, a função se torna uma função linear.

4) Qual é outro nome para a forma padrão de uma função quadrática?

5) Quais dois métodos algébricos podem ser usados para encontrar os interceptos horizontais de uma função quadrática?

Responda

Se possível, podemos usar a fatoração. Caso contrário, podemos usar a fórmula quadrática.

Algébrico

Para os exercícios 6-13, reescreva as funções quadráticas na forma padrão e dê o vértice.

6)\(f(x)=x^2−12x+32\)

7)\(g(x)=x^2+2x−3\)

Responda

\(g(x)=(x+1)^2−4\), Vértice\((−1,−4)\)

8)\(f(x)=x^2−x\)

9)\(f(x)=x^2+5x−2\)

Responda

\(f(x)=\left(x+\dfrac{5}{2}\right)^2−\dfrac{33}{4}\), Vértice\(\left(−\dfrac{5}{2},−\dfrac{33}{4}\right)\)

10)\(h(x)=2x^2+8x−10\)

11)\(k(x)=3x^2−6x−9\)

Responda

\(k(x)=3(x−1)^2−12\), Vértice\((1,−12)\)

12)\(f(x)=2x^2−6x\)

13)\(f(x)=3x^2−5x−1\)

Responda

\(f(x)=3\left(x−\dfrac{5}{6}\right)^2−\dfrac{37}{12}\), Vértice\(\left(\dfrac{5}{6},−\dfrac{37}{12}\right)\)

Para os exercícios 14-20, determine se há um valor mínimo ou máximo para cada função quadrática. Encontre o valor e o eixo de simetria.

14)\(y(x)=2x^2+10x+12\)

15)\(f(x)=2x^2−10x+4\)

Responda

O mínimo é\(−\dfrac{17}{2}\) e ocorre em\(\dfrac{5}{2}\). O eixo de simetria é\(x=\dfrac{5}{2}\).

16)\(f(x)=−x^2+4x+3\)

17)\(f(x)=4x^2+x−1\)

Responda

O mínimo é\(−\dfrac{17}{16}\) e ocorre em\(−\dfrac{1}{8}\). O eixo de simetria é\(x=−\dfrac{1}{8}\).

18)\(h(t)=−4t^2+6t−1\)

19)\(f(x)=\dfrac{1}{2}x^2+3x+1\)

Responda

O mínimo é\(−\dfrac{7}{2}\) e ocorre em\(−3\). O eixo de simetria é\(x=−3\).

20)\(f(x)=−\dfrac{1}{3}x^2−2x+3\)

Para os exercícios 21-25, determine o domínio e o alcance da função quadrática.

21)\(f(x)=(x−3)^2+2\)

Responda

O domínio é\((−∞,∞)\). O alcance é\([2,∞)\).

22)\(f(x)=−2(x+3)^2−6\)

23)\(f(x)=x^2+6x+4\)

Responda

O domínio é\((−∞,∞)\). O alcance é\([−5,∞)\).

24)\(f(x)=2x^2−4x+2\)

25)\(k(x)=3x^2−6x−9\)

Responda

O domínio é\((−∞,∞)\). O alcance é\([−12,∞)\).

Para os exercícios 26-44, resolva as equações sobre os números complexos.

26)\(x^2=−25\)

27)\(x^2=−8\)

Responda

\({2i \sqrt{2},−2i \sqrt{2}}\)

28)\(x^2+36=0\)

29)\(x^2+27=0\)

Responda

\({3i \sqrt{3},−3i\sqrt{3}}\)

30)\(x^2+2x+5=0\)

31)\(x^2−4x+5=0\)

Responda

\({2+i,2−i}\)

32)\(x^2+8x+25=0\)

33)\(x^2−4x+13=0\)

Responda

\({2+3i,2−3i}\)

34)\(x^2+6x+25=0\)

(35)\(x^2−10x+26=0\)

Responda

\({5+i,5−i}\)

36)\(x^2−6x+10=0\)

37)\(x(x−4)=20\)

Responda

\({2+2 \sqrt{6}, 2−2\sqrt{6}}\)

38)\(x(x−2)=10\)

39)\(2x^2+2x+5=0\)

Responda

\(\left\{−\dfrac{1}{2}+\dfrac{3}{2}i, −\dfrac{1}{2}−\dfrac{3}{2}i\right\}\)

40)\(5x^2−8x+5=0\)

41)\(5x^2+6x+2=0\)

Responda

\(\left\{−\dfrac{3}{5}+\dfrac{1}{5}i, −\dfrac{3}{5}−\dfrac{1}{5}i\right\}\)

(42)\(2x^2−6x+5=0\)

43)\(x^2+x+2=0\)

Responda

\(\left\{−\dfrac{1}{2}+\dfrac{1}{2}i\sqrt{7}, −\dfrac{1}{2}−\dfrac{1}{2}i\sqrt{7}\right\}\)

44)\(x^2−2x+4=0\)

Para os exercícios 45-52, use o vértice\((h,k)\) e um ponto no gráfico\((x,y)\) para encontrar a forma geral da equação da função quadrática.

45)\((h,k)=(2,0),(x,y)=(4,4)\)

Responda

\(f(x)=x^2−4x+4\)

(46)\((h,k)=(−2,−1),(x,y)=(−4,3)\)

47)\((h,k)=(0,1),(x,y)=(2,5)\)

Responda

\(f(x)=x^2+1\)

48)\((h,k)=(2,3),(x,y)=(5,12)\)

49)\((h,k)=(−5,3),(x,y)=(2,9)\)

Responda

\(f(x)=\dfrac{6}{49}x^2+\dfrac{60}{49}x+\dfrac{297}{49}\)

50)\((h,k)=(3,2),(x,y)=(10,1)\)

51)\((h,k)=(0,1),(x,y)=(1,0)\)

Responda

\(f(x)=−x^2+1\)

52)\((h,k)=(1,0),(x,y)=(0,1)\)

Gráfica

Para os exercícios 53-58, esboce um gráfico da função quadrática e forneça o vértice, o eixo de simetria e os interceptos.

53)\(f(x)=x^2−2x\)

Responda

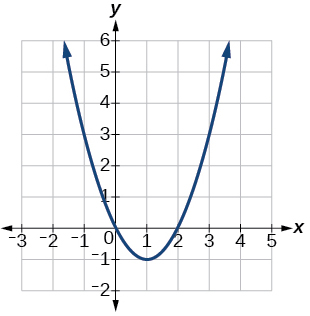
Vértice\((1, −1)\), Eixo de simetria é\(x=1\). As interceptações são\((0,0), (2,0)\).

54)\(f(x)=x^2−6x−1\)

55)\(f(x)=x^2−5x−6\)

Responda

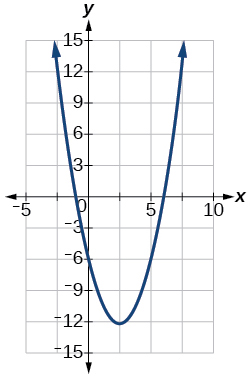
Vértice\(\left(\dfrac{5}{2},\dfrac{−49}{4}\right)\), Eixo de simetria é\(x=\dfrac{5}{2}\). As interceptações são\((0,−6),(−1,0),(6,0)\).

(56)\(f(x)=x^2−7x+3\)

57)\(f(x)=−2x^2+5x−8\)

Responda

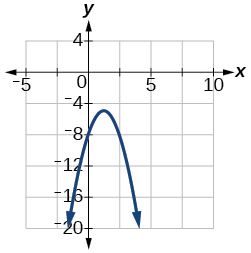
Vértice\(\left(\dfrac{5}{4}, −\dfrac{39}{8}\right)\), Eixo de simetria é\(x=\dfrac{5}{4}\). As interceptações são\((0, −8)\).

(58)\(f(x)=4x^2−12x−3\)

Responda

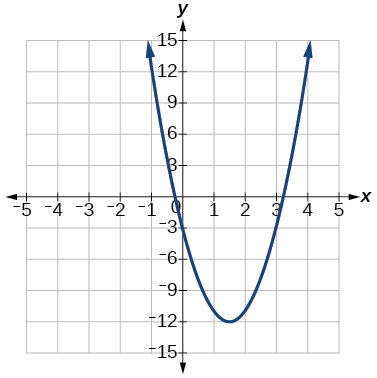
Para os exercícios 59-64, escreva a equação para a função representada graficamente.

59)

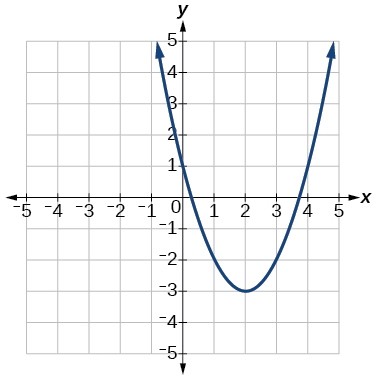
Responda

\(f(x)=x^2−4x+1\)

60)

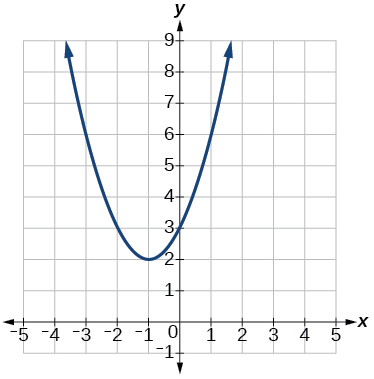
61)

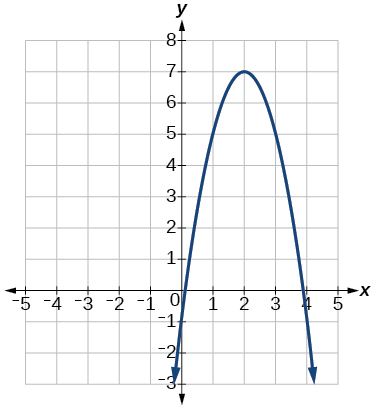
Responda

\(f(x)=−2x^2+8x−1\)

62)

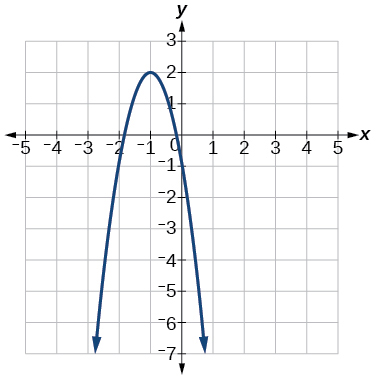
63)

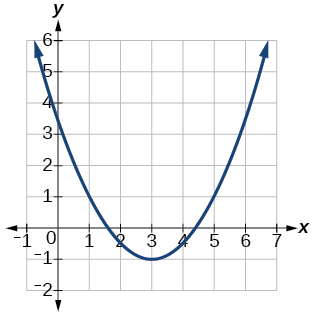
Responda

\(f(x)=\dfrac{1}{2}x^2−3x+\dfrac{7}{2}\)

64)

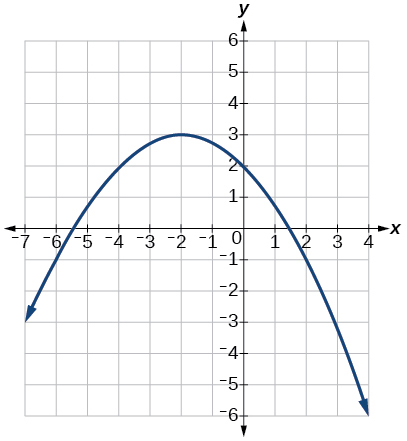
Numérico

Para os exercícios 65-69, use a tabela de valores que representam pontos no gráfico de uma função quadrática. Ao determinar o vértice e o eixo de simetria, encontre a forma geral da equação da função quadrática.

65)

\(x\)	—2	—1	0	1	2
\(y\)	5	2	1	2	5

Responda

\(f(x)=x^2+1\)

66)

\(x\)	—2	—1	0	1	2
\(y\)	1	0	1	4	9

67)

\(x\)	—2	—1	0	1	2
\(y\)	—2	1	2	1	—2

Responda

\(f(x)=2−x^2\)

68)

\(x\)	—2	—1	0	1	2
\(y\)	—8	—3	0	1	0

69)

\(x\)	—2	—1	0	1	2
\(y\)	8	2	0	2	8

Responda

\(f(x)=2x^2\)

Tecnologia

Para os exercícios 70-74, use uma calculadora para encontrar a resposta.

70) Faça um gráfico no mesmo conjunto de eixos das funções\(f(x)=x^2,f(x)=2x^2,\)\(f(x)=\dfrac{1}{3}x^2\) e. O que parece ser o efeito de mudar o coeficiente?

71) Gráfico no mesmo conjunto de eixos\(f(x)=x^2,f(x)=x^2+2\)\(f(x)=x^2,f(x)=x^2+5\) e\(f(x)=x^2−3\) e. O que parece ser o efeito de adicionar uma constante?

Responda

O gráfico é deslocado para cima ou para baixo (um deslocamento vertical).

72) Gráfico no mesmo conjunto de eixos\(f(x)=x^2,f(x)=(x−2)^2,f(x−3)2,\)\(f(x)=(x+4)^2\) e. Qual parece ser o efeito de somar ou subtrair esses números?

73) O caminho de um objeto projetado em um ângulo de\(45\) graus com velocidade inicial de\(80\) pés por segundo é dado pela função\(h(x)=−\dfrac{32}{(80)^2}x^2+x\) onde\(x\) é a distância horizontal percorrida e\(h(x)\) é a altura em pés. Use o recurso TRACE da sua calculadora para determinar a altura do objeto quando ele se afasta\(100\) alguns metros horizontalmente.

Responda

\(50\)pés

74) Uma ponte suspensa pode ser modelada pela função quadrática\(h(x)=.0001x^2\) com\(−2000≤x≤2000\) onde\(|x|\) está o número de pés do centro e\(h(x)\) sua altura em pés. Use o recurso TRACE da sua calculadora para estimar a que distância do centro a ponte tem\(100\) pés de altura.

Extensões

Para os exercícios 75-78, use o vértice do gráfico da função quadrática e a direção em que o gráfico se abre para encontrar o domínio e o alcance da função.

75) Vértice\((1,−2)\), abre.

Responda

O domínio é\((−∞,∞)\). O alcance é\([−2,∞)\).

76) O vértice\((−1,2)\) se abre.

77) Vértice\((−5,11)\), abre para baixo.

Responda

Domínio é\((−∞,∞)\) Intervalo é\((−∞,11]\).

78) Vértice\((−100,100)\), abre.

Para os exercícios 79-84, escreva a equação da função quadrática que contém o ponto dado e tem a mesma forma da função dada.

79) Contém\((1,1)\) e tem a forma de\(f(x)=2x^2\). O vértice está no\(y\) eixo -.

Responda

\(f(x)=2x^2−1\)

80) Contém\((−1,4)\) e tem a forma de\(f(x)=2x^2\). O vértice está no\(y\) eixo -.

81) Contém\((2,3)\) e tem a forma de\(f(x)=3x^2\). O vértice está no\(y\) eixo -.

Responda

\(f(x)=3x^2−9\)

82) Contém\((1,−3)\) e tem a forma de\(f(x)=−x^2\). O vértice está no\(y\) eixo -.

83) Contém\((4,3)\) e tem a forma de\(f(x)=5x^2\). O vértice está no\(y\) eixo -.

Responda

\(f(x)=5x^2−77\)

84) Contém\((1,−6)\) tem a forma de\(f(x)=3x^2\). O vértice tem\(x\) coordenada -de\(-1\).

Aplicativos do mundo real

85) Encontre as dimensões do curral retangular produzindo a maior área fechada com\(200\) pés de cerca.

Responda

\(50\)pés por\(50\) pés. Maximizar\(f(x)=−x^2+100x\).

86) Encontre as dimensões do curral retangular dividido em\(2\) canetas do mesmo tamanho, produzindo a maior área fechada possível com\(300\) pés de cerca.

87) Encontre as dimensões do curral retangular produzindo a maior área fechada dividida em\(3\) canetas do mesmo tamanho, dados\(500\) os pés de cerca.

Responda

\(125\)pés por\(62.5\) pés. Maximizar\(f(x)=−2x^2+250x\).

88) Entre todos os pares de números cuja soma é\(6\), encontre o par com o maior produto. O que é o produto?

89) Entre todos os pares de números cuja diferença é\(12\), encontre o par com o menor produto. O que é o produto?

Responda

\(6\)e\(-\) 6; o produto é\(-36\); maximizar\(f(x)=x^2+12x\).

90) Suponha que o preço por unidade em dólares da produção de um telefone celular seja modelado por\(p=$45−0.0125x\), onde\(x\) está em milhares de telefones produzidos, e a receita representada por milhares de dólares é\(R=x⋅p\). Encontre o nível de produção que maximizará a receita.

91) Um foguete é lançado no ar. Sua altura, em metros acima do nível do mar, em função do tempo, em segundos, é dada por\(h(t)=−4.9t^2+229t+234\). Encontre a altura máxima que o foguete atinge.

Responda

\(2909.56\)metros

92) Uma bola é lançada no ar do topo de um prédio. Sua altura, em metros acima do solo, em função do tempo, em segundos, é dada por\(h(t)=−4.9t^2+24t+8\). Quanto tempo leva para atingir a altura máxima?

93) Um estádio de futebol abriga\(62,000\) espectadores. Com um preço de ingresso de\(\$11\), o comparecimento médio tem sido\(26,000\). Quando o preço caiu para\(\$9\), a frequência média subiu para\(31,000\). Supondo que a participação esteja linearmente relacionada ao preço do ingresso, qual preço do ingresso maximizaria a receita?

Responda

\(\$10.70\)

94) Um fazendeiro descobre que, se plantar\(75\) árvores por acre, cada árvore produzirá\(20\) alqueires de frutos. Ela estima que para cada árvore adicional plantada por acre, o rendimento de cada árvore diminuirá em\(3\) alqueires. Quantas árvores ela deve plantar por acre para maximizar sua colheita?

3.3 Funções de potência e funções polinomiais

Verbal

1) Explique a diferença entre o coeficiente de uma função de potência e seu grau.

Responda

O coeficiente da função de potência é o número real que é multiplicado pela variável elevada a uma potência. O grau é a maior potência que aparece na função.

2) Se uma função polinomial estiver na forma fatorada, qual seria um bom primeiro passo para determinar o grau da função?

3) Em geral, explique o comportamento final de uma função de potência com grau ímpar se o coeficiente principal for positivo.

Responda

À medida que\(x\) diminui sem limites, o mesmo acontece\(f(x)\). À medida que\(x\) aumenta sem limites, o mesmo acontece\(f(x)\).

4) Qual é a relação entre o grau de uma função polinomial e o número máximo de pontos de inflexão em seu gráfico?

5) O que podemos concluir se, em geral, o gráfico de uma função polinomial exibir o seguinte comportamento final? Como\(x \rightarrow-\infty, f(x) \rightarrow-\infty\) e como\(x \rightarrow \infty, f(x) \rightarrow-\infty\).

Responda

A função polinomial é de grau par e o coeficiente principal é negativo.

Algébrico

Para os exercícios 6-11, identifique a função como uma função de potência, uma função polinomial ou nenhuma.

6)\(f(x)=x^5\)

7)\(f(x)=(x^2)^3\)

Responda

Função de alimentação

8)\(f(x)=x−x^4\)

9)\(f(x)=\dfrac{x^2}{x^2−1}\)

Responda

Nem

10)\(f(x)=2x(x+2)(x−1)^2\)

11)\(f(x)=3^{x+1}\)

Responda

Nem

Para os exercícios 12-16, encontre o grau e o coeficiente principal para o polinômio fornecido.

12)\(−3x^4\)

13)\(7−2x^2\)

Responda

Grau =\(2\), Coeficiente =\(-2\)

14)\(−2x^2− 3x^5+ x−6\)

15)\(x(4−x^2)(2x+1)\)

Responda

Grau =\(4\), Coeficiente =\(-2\)

16)\(x^2(2x−3)^2\)

Para os exercícios 17-24, determine o comportamento final das funções.

17)\(f(x)=x^4\)

Responda

Como\(x→∞\)\(f(x)→∞\), como\(x→−∞\),\(f(x)→∞\)

18)\(f(x)=x^3\)

19)\(f(x)=−x^4\)

Responda

Como\(x→−∞\)\(f(x)→−∞\), como\(x→∞\),\(f(x)→−∞\)

20)\(f(x)=−x^9\)

21)\(f(x)=−2x^4− 3x^2+ x−1\)

Responda

Como\(x→−∞\)\(f(x)→−∞\), como\(x→∞\),\(f(x)→−∞\)

22)\(f(x)=3x^2+ x−2\)

23)\(f(x)=x^2(2x^3−x+1)\)

Responda

Como\(x→∞\)\(f(x)→∞\), como\(x→−∞\),\(f(x)→−∞\)

24)\(f(x)=(2−x)^7\)

Para os exercícios 25-30, encontre os interceptos das funções.

25)\(f(t)=2(t−1)(t+2)(t−3)\)

Responda

\(y\)-interceptar é\((0,12)\),\(t\) -interceptos são\((1,0);(–2,0); \)\((3,0)\) e.

26)\(g(n)=−2(3n−1)(2n+1)\)

27)\(f(x)=x^4−16\)

Responda

\(y\)-interceptar é\((0,−16)\),\(x\) -interceptos são\((2,0)\)\((−2,0)\) e.

28)\(f(x)=x^3+27\)

29)\(f(x)=x(x^2−2x−8)\)

Responda

\(y\)-interceptar é\((0,0)\),\(x\) -interceptos são\((0,0),(4,0),\)\((−2, 0)\) e.

30)\(f(x)=(x+3)(4x^2−1)\)

Gráfica

Para os exercícios 31-38, determine o menor grau possível da função polinomial mostrada.

31)

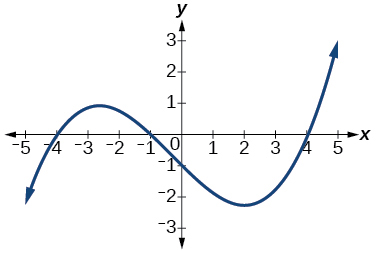
Responda

\(3\)

32)

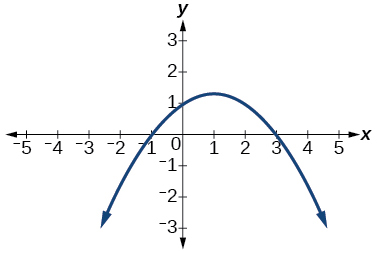
33)

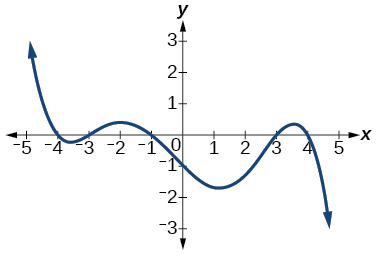
Responda

\(5\)

34)

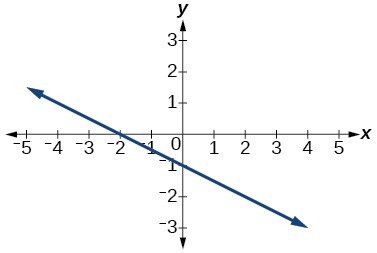
35)

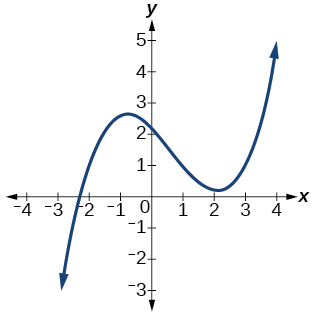
Responda

\(3\)

36)

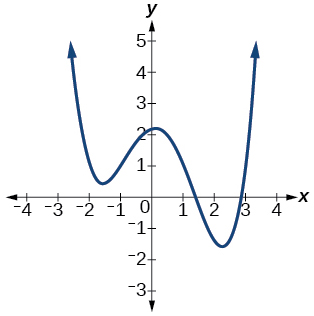
37)

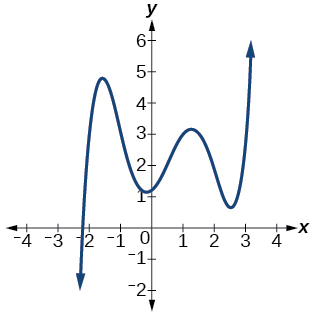
Responda

\(5\)

38)

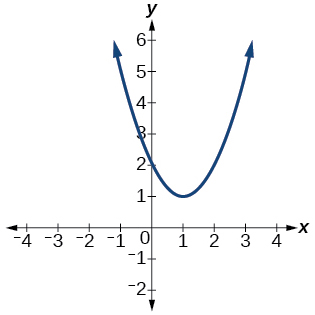
Para os exercícios 39-45, determine se o gráfico da função fornecida é um gráfico de uma função polinomial. Em caso afirmativo, determine o número de pontos de inflexão e o menor grau possível para a função.

39)

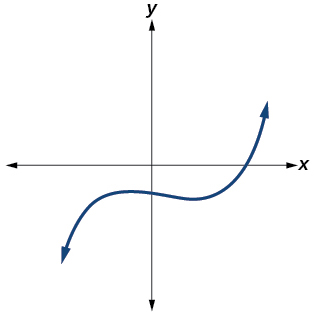
Responda

Sim. O número de pontos de inflexão é\(2\). O menor grau possível é\(3\).

40)

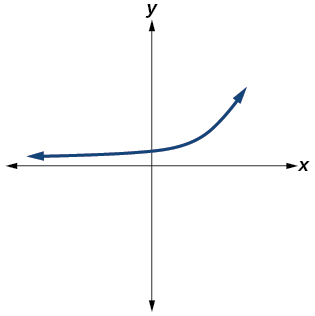
41)

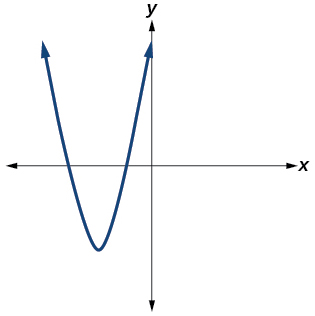
Responda

Sim. O número de pontos de inflexão é\(1\). O menor grau possível é\(2\).

42)

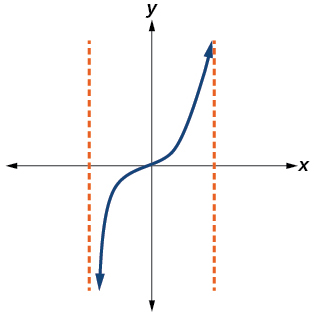
43)

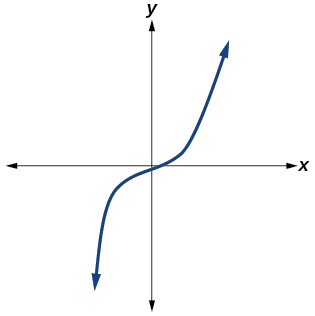
Responda

Sim. O número de pontos de inflexão é\(0\). O menor grau possível é\(1\).

44)

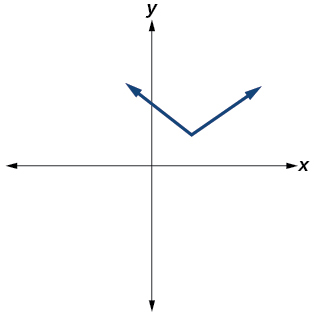
Responda

Não.

45)

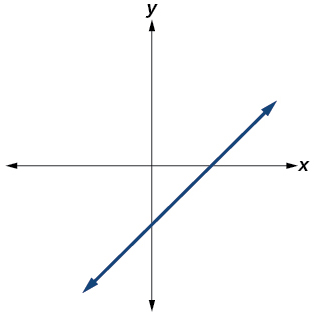
Responda

Sim. O número de pontos de inflexão é\(0\). O menor grau possível é\(1\).

Numérico

Para os exercícios 46-50, faça uma tabela para confirmar o comportamento final da função.

(46)\(f(x)=−x^3\)

47)\(f(x)=x^4−5x^2\)

Responda

\(x\)	\(f(x)\)
\ (x\) ">10	\ (f (x)\) ">9.500
\ (x\) ">100	\ (f (x)\) ">99.950.000
\ (x\) ">—10	\ (f (x)\) ">9.500
\ (x\) ">—100	\ (f (x)\) ">99.950.000

como\(x→−∞,\)\(f(x)→∞\), como\(x→∞,\)\(f(x)→∞\)

48)\(f(x)=x^2(1−x)^2\)

49)\(f(x)=(x−1)(x−2)(3−x)\)

Responda

\(x\)	\(f(x)\)
\ (x\) ">10	\ (f (x)\) ">—504
\ (x\) ">100	\ (f (x)\) ">—941.094
\ (x\) ">—10	\ (f (x)\) ">1.716
\ (x\) ">—100	\ (f (x)\) ">1.061.106

como\(x→−∞,\)\(f(x)→∞\), como\(x→∞,\)\(f(x)→−∞\)

50)\(f(x)=\dfrac{x^5}{10}−x^4\)

Tecnologia

Para os exercícios 51-60, represente graficamente as funções polinomiais usando uma calculadora. Com base no gráfico, determine as interceptações e o comportamento final.

51)\(f(x)=x^3(x−2)\)

Responda

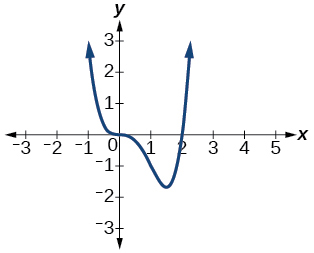
O\(y\) intercepto -é\((0, 0)\). Os interceptos x são As\(x→−∞,\)\(f(x)→∞\),\((0, 0), (2, 0).\) como\(x→∞,\)\(f(x)→∞\)

52)\(f(x)=x(x−3)(x+3)\)

53)\(f(x)=x(14−2x)(10−2x)\)

Responda

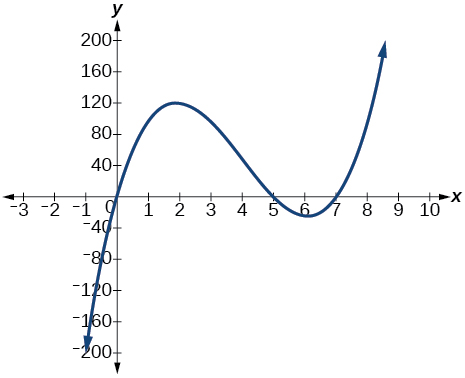
O\(y\) intercepto -é\((0,0)\). Os interceptos x são\((0, 0), (5, 0), (7, 0)\). Como\(x→−∞\)\(f(x)→−∞\), como\(x→∞,\)\(f(x)→∞\)

54)\(f(x)=x(14−2x)(10−2x)^2\)

55)\(f(x)=x^3−16x\)

Responda

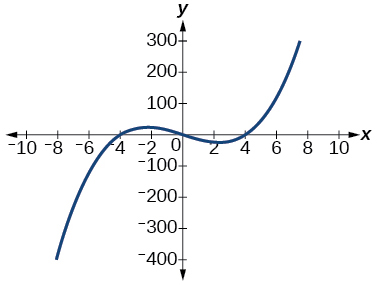
O\(y\) intercepto -é\((0, 0)\). O intercepto x é\((−4, 0), (0, 0), (4, 0)\). Como\(x→−∞\)\(f(x)→−∞\), como\(x→∞,\)\(f(x)→∞\)

(56)\(f(x)=x^3−27\)

57)\(f(x)=x^4−81\)

Responda

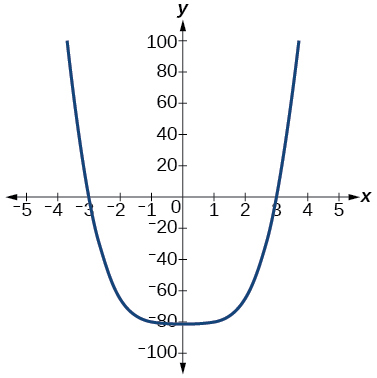
O\(y\) intercepto -é\((0, -81)\). Os\(x\) interceptos -são\((3, 0), (−3, 0)\). Como\(x→−∞,\)\(f(x)→∞\), como\(x→∞,\)\(f(x)→∞\)

(58)\(f(x)=−x^3+x^2+2x\)

(59)\(f(x)=x^3−2x^2−15x\)

Responda

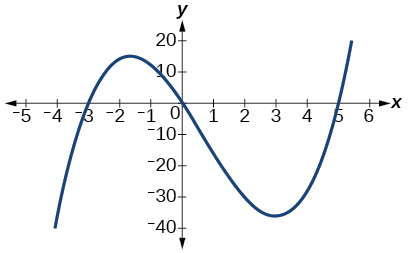
O\(y\) intercepto -é\((0, 0)\). Os interceptos x são As\((−3, 0), (0, 0), (5, 0).\)\(x→−∞\),\(f(x)→−∞\), como\(x→∞,\)\(f(x)→∞\)

60)\(f(x)=x^3−0.01x\)

Extensões

Para os exercícios 61-65, use as informações sobre o gráfico de uma função polinomial para determinar a função. Suponha que o coeficiente principal seja\(1\) ou\(-1\). Pode haver mais de uma resposta correta.

61) O\(y\) intercepto -é\((0,−4)\). As\(x\) interceptações -são\((−2,0), (2,0)\). O diploma é\(2\).

Comportamento final: como\(x→−∞,\)\(f(x)→∞\), como\(x→∞,\)\(f(x)→∞\).

Responda

\(f(x)=x^2−4\)

62) O\(y\) intercepto -é\((0,9)\). As\(x\) interceptações -são\((−3,0), (3,0)\). O diploma é\(2\).

Comportamento final: como\(x→−∞,\)\(f(x)→−∞\), como\(x→∞,\)\(f(x)→−∞\).

63) O\(y\) intercepto -é\((0,0)\). As\(x\) interceptações -são\((0,0), (2,0)\). O diploma é\(3\).

Comportamento final: como\(x→−∞,\)\(f(x)→−∞\), como\(x→∞,\)\(f(x)→∞\).

Responda

\(f(x)=x^3−4x^2+4x\)

64) O\(y\) intercepto -é\((0,1)\). O intercepto x é\((1,0)\). O diploma é\(3\).

Comportamento final: como\(x→−∞\)\(f(x)→∞\),, como\(x→∞\),\(f(x)→−∞\).

65) O\(y\) intercepto -é\((0,1)\). Não há\(x\) interceptação. O diploma é\(4\).

Comportamento final: como\(x→−∞,\)\(f(x)→∞\), como\(x→∞,\)\(f(x)→∞\).

Responda

\(f(x)=x^4+1\)

Aplicativos do mundo real

Para os exercícios 66-70, use as declarações escritas para construir uma função polinomial que represente as informações necessárias.

66) Uma mancha de óleo está se expandindo como um círculo. O raio do círculo está aumentando à taxa de\(20\) metros por dia. Expresse a área do círculo em função do\(d\) número de dias decorridos.

67) Um cubo tem uma borda de\(3\) pés. A borda está aumentando à taxa de\(2\) pés por minuto. Expresse o volume do cubo em função do\(m\) número de minutos decorridos.

Responda

\(V(m)=8m^3+36m^2+54m+27\)

68) Um retângulo tem um comprimento de\(10\) polegadas e uma largura de\(6\) polegadas. Se o comprimento for aumentado em\(x\) polegadas e a largura aumentada em duas vezes essa quantidade, expresse a área do retângulo em função de\(x\).

69) Uma caixa aberta deve ser construída cortando cantos\(x\) quadrados de lados em polegadas de um pedaço de papelão\(8\) polegadas por\(8\) polegadas e depois dobrando as laterais. Expresse o volume da caixa em função de\(x\).

Responda

\(V(x)=4x^3−32x^2+64x\)

70) Um retângulo tem o dobro do comprimento que é largo. Quadrados de\(2\) pés laterais são cortados em cada canto. Em seguida, os lados são dobrados para formar uma caixa aberta. Expresse o volume da caixa em função da largura (\(x\)).

3.4 Gráficos de funções polinomiais

Verbal

1) Qual é a diferença entre um\(x\) intercepto -e um zero de uma função polinomial\(f\)?

Responda

O\(x\) -intercept é onde o gráfico da função cruza o\(x\) eixo -e o zero da função é o valor de entrada para o qual\(f(x)=0\).

2) Se uma função polinomial de grau\(n\) tem zeros\(n\) distintos, o que você sabe sobre o gráfico da função?

3) Explique como o Teorema do Valor Intermediário pode nos ajudar a encontrar o zero de uma função.

Responda

Se avaliarmos a função em\(a\) e em\(b\) e o sinal do valor da função mudar, saberemos que existe um zero entre\(a\)\(b\) e.

4) Explique como a forma fatorada do polinômio nos ajuda a representá-lo graficamente.

5) Se o gráfico de um polinômio apenas tocar o\(x\) eixo -e depois mudar de direção, o que podemos concluir sobre a forma fatorada do polinômio?

Responda

Haverá um fator elevado a uma potência uniforme.

Algébrico

Para os exercícios 6-23, encontre os\(t\) interceptos\(x\) -ou -das funções polinomiais.

6)\(C(t)=2(t−4)(t+1)(t−6)\)

7)\(C(t)=3(t+2)(t−3)(t+5)\)

Responda

\((−2,0),(3,0),(−5,0)\)

8)\(C(t)=4t(t−2)^2(t+1)\)

9)\(C(t)=2t(t−3)(t+1)^2\)

Responda

\((3,0),(−1,0),(0,0)\)

10)\(C(t)=2t^4−8t^3+6t^2\)

11)\(C(t)=4t^4+12t^3−40t^2\)

Responda

\((0,0), (−5,0), (2,0)\)

12)\(f(x)=x^4−x^2\)

13)\(f(x)=x^3+x^2−20x\)

Responda

\((0,0), (−5,0), (4,0)\)

14)\(f(x)=x^3+6x^2−7x\)

15)\(f(x)=x^3+x^2−4x−4\)

Responda

\((2,0), (−2,0), (−1,0)\)

16)\(f(x)=x^3+2x^2−9x−18\)

17)\(f(x)=2x^3−x^2−8x+4\)

Responda

\((−2,0),(2,0),\left(\dfrac{1}{2},0\right)\)

18)\(f(x)=x^6−7x^3−8\)

19)\(f(x)=2x^4+6x^2−8\)

Responda

\((1,0), (−1,0)\)

20)\(f(x)=x^3−3x^2−x+3\)

21)\(f(x)=x^6−2x^4−3x^2\)

Responda

\((0,0),(\sqrt{3},0),(−\sqrt{3},0)\)

22)\(f(x)=x^6−3x^4−4x^2\)

23)\(f(x)=x^5−5x^3+4x\)

Responda

\((0,0), (1,0), (−1,0), (2,0), (−2,0)\)

Para os exercícios 24-29, use o Teorema do Valor Intermediário para confirmar que o polinômio dado tem pelo menos um zero dentro do intervalo determinado.

24)\(f(x)=x^3−9x\), entre\(x=−4\)\(x=−2\) e.

25)\(f(x)=x^3−9x\), entre\(x=2\)\(x=4\) e.

Responda

\(f(2)=–10\)\(f(4)=28\)e. A alteração do sinal confirma.

26)\(f(x)=x^5−2x\), entre\(x=1\)\(x=2\) e.

27)\(f(x)=−x^4+4\), entre\(x=1\)\(x=3\) e.

Responda

\(f(1)=3\)e a alteração do\(f(3)=–77.\) sinal confirma.

28)\(f(x)=−2x^3−x\), entre\(x=–1\)\(x=1\) e.

29)\(f(x)=x^3−100x+2\), entre\(x=0.01\) e\(x=0.1\)

Responda

\(f(0.01)=1.000001 \)\(f(0.1)=–7.999\)e. A alteração do sinal confirma.

Para os exercícios 30-41, encontre os zeros e dê a multiplicidade de cada um.

30)\(f(x)=(x+2)^3(x−3)^2\)

31)\(f(x)=x^2(2x+3)^5(x−4)^2\)

Responda

\(0\)com multiplicidade\(2\),\(−\dfrac{3}{2}\) com multiplicidade\(5\),\(4\) com multiplicidade\(2\)

32)\(f(x)=x^3(x−1)^3(x+2)\)

33)\(f(x)=x^2(x^2+4x+4)\)

Responda

\(0\)com multiplicidade\(2\),\(-2\) com multiplicidade\(2\)

34)\(f(x)=(2x+1)^3(9x^2−6x+1)\)

(35)\(f(x)=(3x+2)^5(x^2−10x+25)\)

Responda

\(−\dfrac{2}{3}\)com multiplicidade\(5\),\(5\) com multiplicidade\(2\)

36)\(f(x)=x(4x^2−12x+9)(x^2+8x+16)\)

37)\(f(x)=x^6−x^5−2x^4\)

Responda

\(0\)com multiplicidade\(4\),\(2\) com multiplicidade\(1\),\(-1\) com multiplicidade\(1\)

38)\(f(x)=3x^4+6x^3+3x^2\)

39)\(f(x)=4x^5−12x^4+9x^3\)

Responda

\(\dfrac{3}{2}\)com multiplicidade\(2\),\(0\) com multiplicidade\(3\)

40)\(f(x)=2x^4(x^3−4x^2+4x)\)

41)\(f(x)=4x^4(9x^4−12x^3+4x^2)\)

Responda

\(0\)com multiplicidade\(6\),\(\dfrac{2}{3}\) com multiplicidade\(2\)

Gráfica

Para os exercícios 42-47, represente graficamente as funções polinomiais. Observe\(x\) - e\(y\) - intercepta, multiplicidade e comportamento final.

(42)\(f(x)=(x+3)^2(x−2)\)

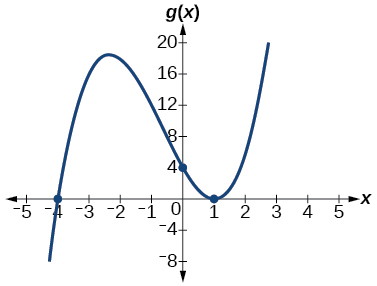
43)\(g(x)=(x+4)(x−1)^2\)

Responda

\(x\)-intercepta,\((1, 0)\) com multiplicidade\(2\),\((–4, 0)\) com multiplicidade\(1\),\(y\) - intercepta\((0, 4)\). Como\(x→−∞\)\(f(x)→−∞\), como\(x→∞,\)\(f(x)→∞\).

44)\(h(x)=(x−1)^3(x+3)^2\)

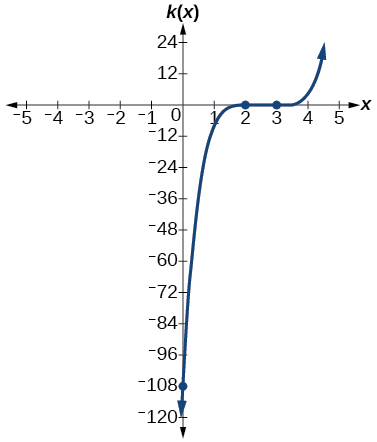
45)\(k(x)=(x−3)^3(x−2)^2\)

Responda

\(x\)-intercepta\((3,0)\) com multiplicidade\(3\),\((2,0)\) com multiplicidade\(2\),\(y\) - intercepta As\(x→−∞,\)\(f(x)→−∞\),\((0,–108).\) como\(x→∞,\)\(f(x)→∞\).

(46)\(m(x)=−2x(x−1)(x+3)\)

47)\(n(x)=−3x(x+2)(x−4)\)

Responda

\(x\)-intercepta\((0, 0),(–2, 0),(4, 0)\) com multiplicidade\(1\),\(y\) -intercepta (0, 0). Como\(x→−∞,\)\(f(x)→∞\), como\(x→∞,\)\(f(x)→−∞\).

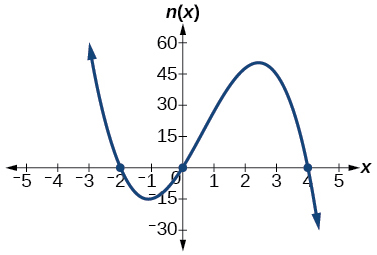
Para os exercícios 48-52, use os gráficos para escrever a fórmula para uma função polinomial de menor grau.

48)

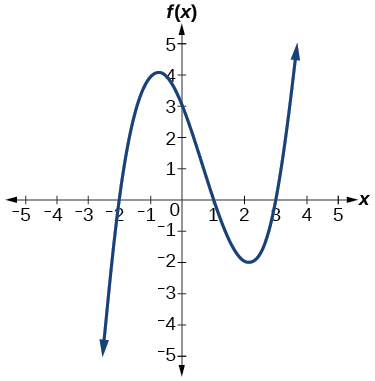
49)

Responda

\(f(x)=−\dfrac{2}{9}(x−3)(x+1)(x+3)\)

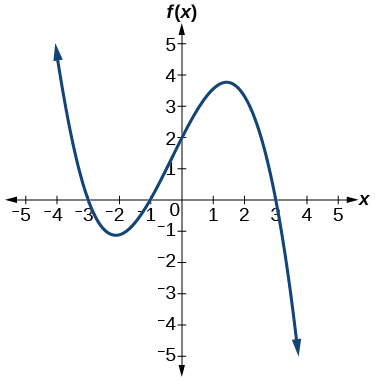
50)

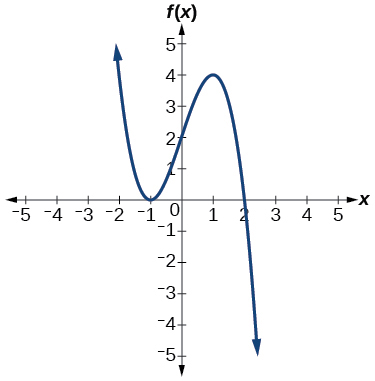
51)

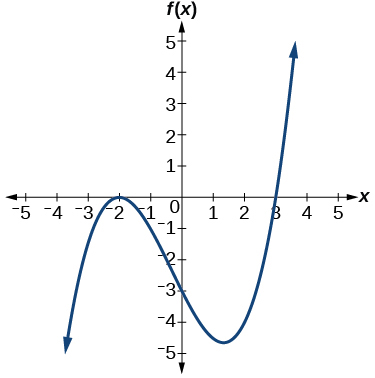
Responda

\(f(x)=\dfrac{1}{4}(x+2)^2(x−3)\)

52)

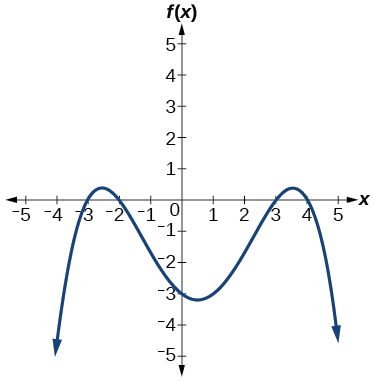
Para os exercícios 53-56, use o gráfico para identificar zeros e multiplicidade.

53)

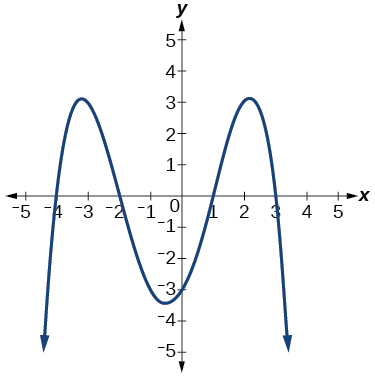
Responda

\(–4, –2, 1, 3\)com multiplicidade\(1\)

54)

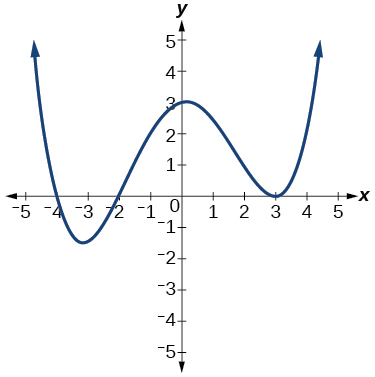
55)

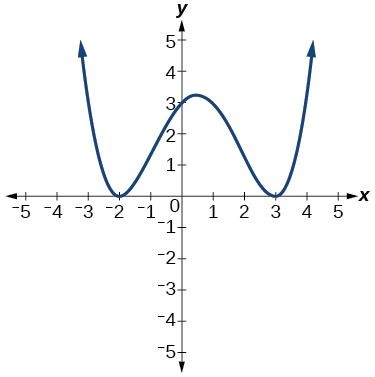
Responda

\(–2, 3\)cada um com multiplicidade\(2\)

56)

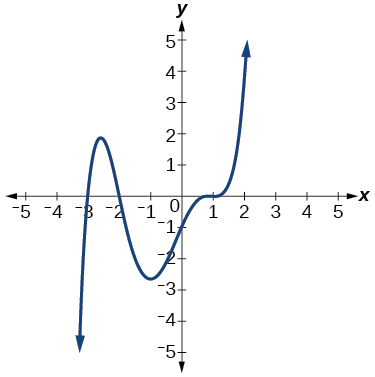
Para os exercícios 57-66, use as informações fornecidas sobre o gráfico polinomial para escrever a equação.

57) Grau\(3\). Zeros em\(x=–2\)\(x=1\),\(x=3\) e. \(y\)-interceptar em\((0,–4)\)

Responda

\(f(x)=−\dfrac{2}{3}(x+2)(x−1)(x−3)\)

58) Grau\(3\). Zeros em\(x=–5\)\(x=–2\),\(x=1\) e. \(y\)-interceptar em\((0,6)\)

59) Grau\(5\). Raízes da multiplicidade\(2\) em\(x=3\) e\(x=1\), e uma raiz da multiplicidade\(1\) em\(x=–3\). \(y\)-interceptar em\((0,9)\)

Responda

\(f(x)=\dfrac{1}{3}(x−3)^2(x−1)^2(x+3)\)

60) Grau\(4\). Raiz da multiplicidade\(2\) em\(x=4\), e raízes da multiplicidade\(1\) em\(x=1\)\(x=–2\) e. \(y\)-interceptar em\((0,–3)\)

61) Grau\(5\). Zero duplo em\(x=1\) e triplo zero em\(x=3\). Passa pelo ponto\((2,15)\)

Responda

\(f(x)=−15(x−1)^2(x−3)^3\)

62) Grau\(3\). Zeros em\(x=4\)\(x=3\),\(x=2\) e. \(y\)-interceptar em\((0,−24)\)

63) Grau\(3\). Zeros em\(x=−3\),\(x=−2\)\(x=1\) e. \(y\)-interceptar em\((0,12)\)

Responda

\(f(x)=−2(x+3)(x+2)(x−1)\)

64) Grau\(5\). Raízes da multiplicidade\(2\) em\(x=−3\)\(x=2\) e e uma raiz da multiplicidade\(1\) em\(x=−2\). \(y\)-interceptar em\((0, 4)\).

65) Grau\(4\). Raízes da multiplicidade\(2\) em\(x=\dfrac{1}{2}\) e raízes da multiplicidade\(1\) em\(x=6 \)\(x=−2\) e. \(y\)-interceptar em\((0,18)\)

Responda

\(f(x)=−\dfrac{3}{2}(2x−1)^2(x−6)(x+2)\)

66) Zero duplo em\(x=−3\) e triplo zero em\(x=0\). Passa pelo ponto\((1,32)\).

Tecnologia

Para os exercícios 67-71, use uma calculadora para aproximar os mínimos e máximos locais ou os mínimos e máximos globais.

67)\(f(x)=x^3−x−1\)

Responda

máximo local\((–.58, –.62)\), mínimo local\((.58, –1.38)\)

68)\(f(x)=2x^3−3x−1\)

69)\(f(x)=x^4+x\)

Responda

mínimo global\((–.63, –.47)\)

70)\(f(x)=−x^4+3x−2\)

71)\(f(x)=x^4−x^3+1\)

Responda

mínimo global\((.75, .89)\)

Extensões

Para os exercícios 72-74, use os gráficos para escrever uma função polinomial de menor grau.

72)

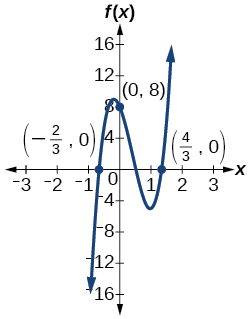
73)

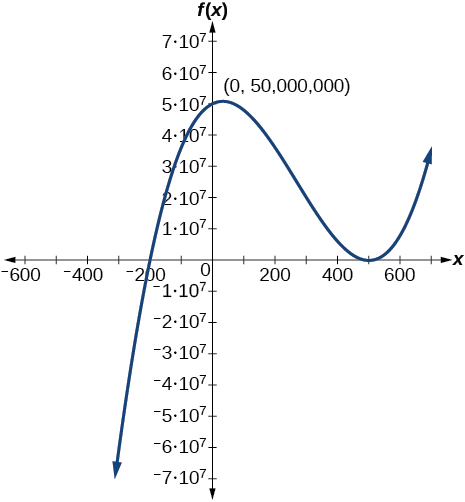
Responda

\(f(x)=(x−500)^2(x+200)\)

74)

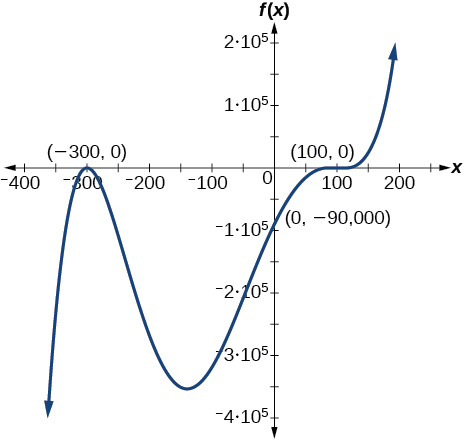
Aplicativos do mundo real

Para os exercícios 75-, escreva a função polinomial que modela a situação dada.

75) Um retângulo tem um comprimento de\(10\) unidades e uma largura de 8 unidades. \(x\)Quadrados de por\(x\) unidades são cortados em cada canto e, em seguida, os lados são dobrados para criar uma caixa aberta. Expresse o volume da caixa como uma função polinomial em termos de\(x\).

Responda

\(f(x)=4x^3−36x^2+80x\)

76) Considere o mesmo retângulo do problema anterior. \(2x\)Quadrados de por\(2x\) unidades são cortados em cada canto. Expresse o volume da caixa como um polinômio em termos de\(x\).

77) Um quadrado tem lados de\(12\) unidades. \(x +1\)Quadrados por\(x +1\) unidades são cortados em cada canto e, em seguida, os lados são dobrados para criar uma caixa aberta. Expresse o volume da caixa como uma função em termos de\(x\).

Responda

\(f(x)=4x^3−36x^2+60x+100\)

78) Um cilindro tem um raio de\(x+2\) unidades e uma altura de\(3\) unidades maior. Expresse o volume do cilindro como uma função polinomial.

79) Um cone circular reto tem um raio\(3x+6\) e uma\(3\) unidade de altura a menos. Expresse o volume do cone como uma função polinomial. O volume de um cone é\(V=\dfrac{1}{3}πr^2h\) para raio\(r\) e altura\(h\).

Responda

\(f(x)=π(9x^3+45x^2+72x+36)\)

3.5 Dividindo polinômios

Verbal

1) Se a divisão de um polinômio por um binômio resultar em um restante de zero, o que pode ser concluído?

Responda

O binômio é um fator do polinômio.

2) Se um polinômio de grau\(n\) é dividido por um binômio de grau\(1\), qual é o grau do quociente?

Algébrico

Para os exercícios 3-13, use a divisão longa para dividir. Especifique o quociente e o restante.

3)\((x^2+5x−1)÷(x−1)\)

Responda

\(\mathrm{x+6+\dfrac{5}{x−1}, quotient: x+6, remainder: 5}\)

4)\((2x^2−9x−5)÷(x−5)\)

5)\((3x^2+23x+14)÷(x+7)\)

Responda

\(\mathrm{3x+2, quotient: 3x+2, remainder: 0}\)

6)\((4x^2−10x+6)÷(4x+2)\)

7)\((6x^2−25x−25)÷(6x+5)\)

Responda

\(\mathrm{x−5, quotient: x−5, remainder: 0}\)

8)\((−x^2−1)÷(x+1)\)

9)\((2x^2−3x+2)÷(x+2)\)

Responda

\(\mathrm{2x−7+\dfrac{16}{x+2}, quotient: 2x−7, remainder: 16}\)

10)\((x^3−126)÷(x−5)\)

11)\((3x^2−5x+4)÷(3x+1)\)

Responda

\(\mathrm{x−2+\dfrac{6}{3x+1}, quotient: x−2, remainder: 6}\)

12)\((x^3−3x^2+5x−6)÷(x−2)\)

13)\((2x^3+3x^2−4x+15)÷(x+3)\)

Responda

\(\mathrm{2x^2−3x+5, quotient: 2x^2−3x+5, remainder: 0}\)

Para os exercícios 14-37, use a divisão sintética para encontrar o quociente.

14)\((3x^3−2x^2+x−4)÷(x+3)\)

15)\((2x^3−6x^2−7x+6)÷(x−4)\)

Responda

\(2x^2+2x+1+\dfrac{10}{x−4}\)

16)\((6x^3−10x^2−7x−15)÷(x+1)\)

17)\((4x^3−12x^2−5x−1)÷(2x+1)\)

Responda

\(2x^2−7x+1−\dfrac{2}{2x+1}\)

18)\((9x^3−9x^2+18x+5)÷(3x−1)\)

19)\((3x^3−2x^2+x−4)÷(x+3)\)

Responda

\(3x^2−11x+34−\dfrac{106}{x+3}\)

20)\((−6x^3+x^2−4)÷(2x−3)\)

21)\((2x^3+7x^2−13x−3)÷(2x−3)\)

Responda

\(x^2+5x+1\)

22)\((3x^3−5x^2+2x+3)÷(x+2)\)

23)\((4x^3−5x^2+13)÷(x+4)\)

Responda

\(4x^2−21x+84−\dfrac{323}{x+4}\)

24)\((x^3−3x+2)÷(x+2)\)

25)\((x^3−21x^2+147x−343)÷(x−7)\)

Responda

\(x^2−14x+49\)

26)\((x^3−15x^2+75x−125)÷(x−5)\)

27)\((9x^3−x+2)÷(3x−1)\)

Responda

\(3x^2+x+\dfrac{2}{3x−1}\)

28)\((6x^3−x^2+5x+2)÷(3x+1)\)

29)\((x^4+x^3−3x^2−2x+1)÷(x+1)\)

Responda

\(x^3−3x+1\)

30)\((x^4−3x^2+1)÷(x−1)\)

31)\((x^4+2x^3−3x^2+2x+6)÷(x+3)\)

Responda

\(x^3−x^2+2\)

32)\((x^4−10x^3+37x^2−60x+36)÷(x−2)\)

33)\((x^4−8x^3+24x^2−32x+16)÷(x−2)\)

Responda

\(x^3−6x^2+12x−8\)

34)\((x^4+5x^3−3x^2−13x+10)÷(x+5)\)

(35)\((x^4−12x^3+54x^2−108x+81)÷(x−3)\)

Responda

\(x^3−9x^2+27x−27\)

36)\((4x^4−2x^3−4x+2)÷(2x−1)\)

37)\((4x^4+2x^3−4x^2+2x+2)÷(2x+1)\)

Responda

\(2x^3−2x+2\)

Para os exercícios 38-43, use a divisão sintética para determinar se a primeira expressão é um fator da segunda. Se for, indique a fatoração.

38)\(x−2, 4x^3−3x^2−8x+4\)

39)\(x−2, 3x^4−6x^3−5x+10\)

Responda

Sim\((x−2)(3x^3−5)\)

40)\(x+3, −4x^3+5x^2+8\)

41)\(x−2, 4x^4−15x^2−4\)

Responda

Sim\((x−2)(4x^3+8x^2+x+2)\)

(42)\(x−\dfrac{1}{2}, 2x^4−x^3+2x−1\)

43)\(x+\dfrac{1}{3}, 3x^4+x^3−3x+1\)

Responda

Não

Gráfica

Para os exercícios 44-48, use o gráfico do polinômio de terceiro grau e um fator para escrever a forma fatorada do polinômio sugerido pelo gráfico. O coeficiente principal é um.

44) O fator é\(x^2−x+3\)

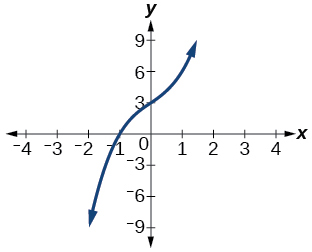
45) O fator é\((x^2+2x+4)\)

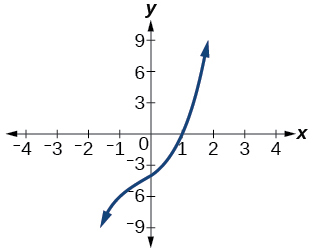
Responda

\((x−1)(x^2+2x+4)\)

46) O fator é\(x^2+2x+5\)

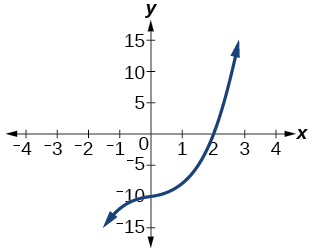
47) O fator é\(x^2+x+1\)

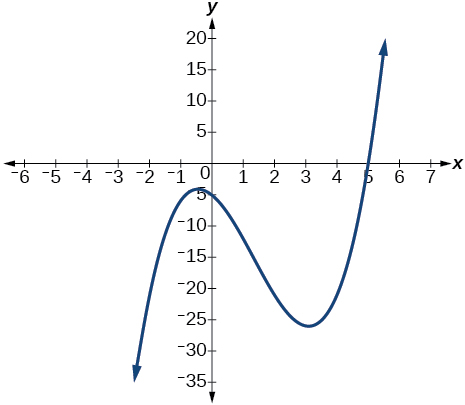
Responda

\((x−5)(x^2+x+1)\)

48) O fator é\(x^2+2x+2\)

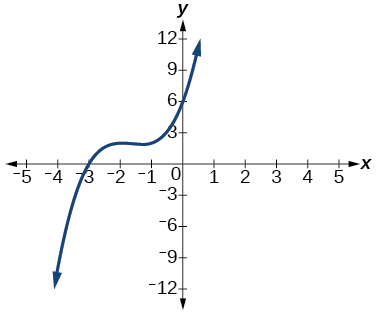
Para os exercícios 49-53, use a divisão sintética para encontrar o quociente e o restante.

49)\(\dfrac{4x^3−33}{x−2}\)

Responda

\(\mathrm{Quotient: 4x^2+8x+16, remainder: −1}\)

50)\(\dfrac{2x^3+25}{x+3}\)

51)\(\dfrac{3x^3+2x−5}{x−1}\)

Responda

\(\mathrm{Quotient: 3x^2+3x+5, remainder: 0}\)

52)\(\dfrac{−4x^3−x^2−12}{x+4}\)

53)\(\dfrac{x^4−22}{x+2}\)

Responda

\(\mathrm{Quotient: x^3−2x^2+4x−8, remainder: −6}\)

Tecnologia

Para os exercícios 54-58, use uma calculadora com CAS para responder às perguntas.

54) Considere\(\dfrac{x^k−1}{x−1}\) com\(k=1, 2, 3\). O que você espera que o resultado seja se\(k=4\)?

55) Considere\(\dfrac{x^k+1}{x+1}\) para\(k=1, 3, 5\). O que você espera que o resultado seja se\(k=7\)?

Responda

\(x^6−x^5+x^4−x^3+x^2−x+1\)

56) Considere\(\dfrac{x^4−k^4}{x−k}\) para\(k=1, 2, 3\). O que você espera que o resultado seja se\(k=4\)?

57) Considere\(\dfrac{x^k}{x+1}\) com\(k=1, 2, 3\). O que você espera que o resultado seja se\(k=4\)?

Responda

\(x^3−x^2+x−1+\dfrac{1}{x+1}\)

58) Considere\(\dfrac{x^k}{x−1}\) com\(k=1, 2, 3\). O que você espera que o resultado seja se\(k=4\)?

Extensões

Para os exercícios 59-63, use a divisão sintética para determinar o quociente envolvendo um número complexo.

(59)\(\dfrac{x+1}{x−i}\)

Responda

\(1+\dfrac{1+i}{x−i}\)

60)\(\dfrac{x^2+1}{x−i}\)

61)\(\dfrac{x+1}{x+i}\)

Responda

\(1+\dfrac{1−i}{x+i}\)

62)\(\dfrac{x^2+1}{x+i}\)

63)\(\dfrac{x^3+1}{x−i}\)

Responda

\(x^2−ix−1+\dfrac{1−i}{x−i}\)

Aplicativos do mundo real

Para os exercícios 64-66, use o comprimento e a área fornecidos de um retângulo para expressar a largura algebricamente.

64) O comprimento é\(x+5\), a área é\(2x^2+9x−5\).

65) O comprimento é\(2x + 5\), a área é\(4x^3+10x^2+6x+15\).

Responda

\(2x^2+3\)

66) O comprimento é\(3x–4\), a área é\(6x^4−8x^3+9x^2−9x−4\).

Para os exercícios 67-70, use o volume dado de uma caixa e seu comprimento e largura para expressar algebricamente a altura da caixa.

67) O volume é\(12x^3+20x^2−21x−36\), o comprimento é\(2x+3\), a largura é\(3x−4\).

Responda

\(2x+3\)

68) O volume é\(18x^3−21x^2−40x+48\), o comprimento é\(3x–4\), a largura é\(3x–4\).

69) O volume é\(10x^3+27x^2+2x−24\), o comprimento é\(5x–4\), a largura é\(2x+3\).

Responda

\(x+2\)

70) O volume é\(10x^3+30x^2−8x−24\), o comprimento é\(2\), a largura é\(x+3\).

Para os exercícios 71-73, use o volume e o raio fornecidos de um cilindro para expressar a altura do cilindro algebricamente.

71) O volume é\(π(25x^3−65x^2−29x−3)\), o raio é\(5x+1\).

Responda

\(x−3\)

72) O volume é\(π(4x^3+12x^2−15x−50)\), o raio é\(2x+5\).

73) O volume é\(π(3x^4+24x^3+46x^2−16x−32)\), o raio é\(x+4\).

Responda

\(3x^2−2\)

3.6 Zeros de funções polinomiais

Verbal

1) Descreva um uso do Teorema do Restante.

Responda

O teorema pode ser usado para avaliar um polinômio.

2) Explique por que o Teorema do Zero Racional não garante encontrar zeros de uma função polinomial.

3) Qual é a diferença entre zeros racionais e reais?

Responda

Os zeros racionais podem ser expressos como frações, enquanto os zeros reais incluem números irracionais.

4) Se a Regra de Sinais de Descartes revelar uma não mudança de sinais ou um sinal de mudança, que conclusão específica pode ser extraída?

5) Se a divisão sintética revelar um zero, por que devemos tentar esse valor novamente como uma possível solução?

Responda

As funções polinomiais podem ter zeros repetidos, então o fato de o número ser zero não impede que seja zero novamente.

Algébrico

Para os exercícios 6-13, use o Teorema do Restante para encontrar o restante.

6)\((x^4−9x^2+14)÷(x−2)\)

7)\((3x^3−2x^2+x−4)÷(x+3)\)

Responda

\(−106\)

8)\((x^4+5x^3−4x−17)÷(x+1)\)

9)\((−3x^2+6x+24)÷(x−4)\)

Responda

\(0\)

10)\((5x^5−4x^4+3x^3−2x^2+x−1)÷(x+6)\)

11)\((x^4−1)÷(x−4)\)

Responda

\(255\)

12)\((3x^3+4x^2−8x+2)÷(x−3)\)

13)\((4x^3+5x^2−2x+7)÷(x+2)\)

Responda

\(−1\)

Para os exercícios 14-21, use o Teorema do Fator para encontrar todos os zeros reais para uma determinada função polinomial e um fator.

14)\(f(x)=2x^3−9x^2+13x−6; x−1\)

15)\(f(x)=2x^3+x^2−5x+2; x+2 \)

Responda

\(−2, 1, \dfrac{1}{2}\)

16)\(f(x)=3x^3+x^2−20x+12; x+3\)

17)\(f(x)=2x^3+3x^2+x+6;x+2\)

Responda

\(−2\)

18)\(f(x)=−5x^3+16x^2−9;x−3\)

19)\(x^3+3x^2+4x+12;x+3\)

Responda

\(−3\)

20)\(4x^3−7x+3;x−1\)

21)\(2x^3+5x^2−12x−30,2x+5\)

Responda

\(−\dfrac{5}{2}, \sqrt{6}, −\sqrt{6}\)

Para os exercícios 22-39, use o Teorema do Zero Racional para encontrar todos os zeros reais.

22)\(x^3−3x^2−10x+24=0\)

23)\(2x^3+7x^2−10x−24=0\)

Responda

\(2, −4, −\dfrac{3}{2}\)

24)\(x^3+2x^2−9x−18=0\)

25)\(x^3+5x^2−16x−80=0\)

Responda

\(4, −4, −5\)

26)\(x^3−3x^2−25x+75=0\)

27)\(2x^3−3x^2−32x−15=0\)

Responda

\(5, −3, −\dfrac{1}{2} \)

28)\(2x^3+x^2−7x−6=0\)

29)\(2x^3−3x^2−x+1=0\)

Responda

\(\dfrac{1}{2}, \dfrac{1+\sqrt{5}}{2}, \dfrac{1−\sqrt{5}}{2}\)

30)\(3x^3−x^2−11x−6=0\)

31)\(2x^3−5x^2+9x−9=0\)

Responda

\(\dfrac{3}{2}\)

32)\(2x^3−3x^2+4x+3=0\)

33)\(x^4−2x^3−7x^2+8x+12=0\)

Responda

\(2, 3, −1, −2\)

34)\(x^4+2x^3−9x^2−2x+8=0\)

(35)\(4x^4+4x^3−25x^2−x+6=0\)

Responda

\(\dfrac{1}{2}, −\dfrac{1}{2}, 2, −3\)

36)\(2x^4−3x^3−15x^2+32x−12=0\)

37)\(x^4+2x^3−4x^2−10x−5=0\)

Responda

\(−1, −1, \sqrt{5}, −\sqrt{5}\)

38)\(4x^3−3x+1=0\)

39)\(8x^4+26x^3+39x^2+26x+6\)

Responda

\(−\dfrac{3}{4}, −\dfrac{1}{2}\)

Para os exercícios 40-45, encontre todas as soluções complexas (reais e não reais).

40)\(x^3+x^2+x+1=0\)

41)\(x^3−8x^2+25x−26=0\)

Responda

\(2, 3+2i, 3−2i\)

(42)\(x^3+13x^2+57x+85=0\)

43)\(3x^3−4x^2+11x+10=0\)

Responda

\(−\dfrac{2}{3}, 1+2i, 1−2i\)

44)\(x^4+2x^3+22x^2+50x−75=0\)

45)\(2x^3−3x^2+32x+17=0\)

Responda

\(−\dfrac{1}{2}, 1+4i, 1−4i\)

Gráfica

Para os exercícios 46-55, use a Regra de Descartes para determinar o número possível de soluções positivas e negativas. Confirme com o gráfico fornecido.

(46)\(f(x)=x^3−1\)

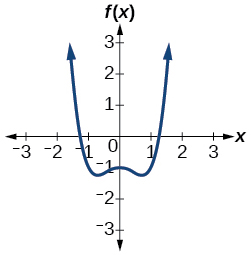
47)\(f(x)=x^4−x^2−1\)

Responda

\(1\)positivo,\(1\) negativo

48)\(f(x)=x^3−2x^2−5x+6\)

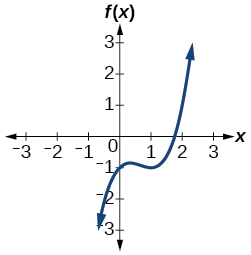
49)\(f(x)=x^3−2x^2+x−1\)

Responda

\(3\)ou\(1\) positivo,\(0\) negativo

50)\(f(x)=x^4+2x^3−12x^2+14x−5\)

51)\(f(x)=2x^3+37x^2+200x+300\)

Responda

\(0\)positivo\(3\) ou\(1\) negativo

52)\(f(x)=x^3−2x^2−16x+32\)

53)\(f(x)=2x^4−5x^3−5x^2+5x+3\)

Responda

\(2\)ou\(0\) positivo\(2\) ou\(0\) negativo

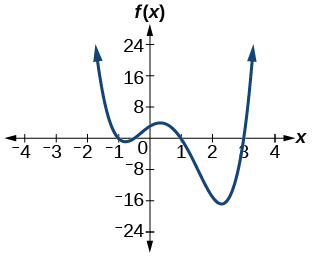
54)\(f(x)=2x^4−5x^3−14x^2+20x+8\)

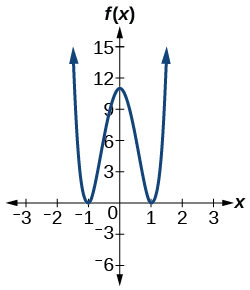
55)\(f(x)=10x^4−21x^2+11\)

Responda

\(2\)ou\(0\) positivo\(2\) ou\(0\) negativo

Numérico

Para os exercícios 56-60, liste todos os zeros racionais possíveis para as funções.

(56)\(f(x)=x^4+3x^3−4x+4\)

57)\(f(x)=2x^3+3x^2−8x+5\)

Responda

\(±5, ±1, ± \dfrac{5}{2}\)

(58)\(f(x)=3x^3+5x^2−5x+4\)

(59)\(f(x)=6x^4−10x^2+13x+1\)

Responda

\(±1, ±\dfrac{1}{2}, ±\dfrac{1}{3}, ±\dfrac{1}{6}\)

60)\(f(x)=4x^5−10x^4+8x^3+x^2−8\)

Tecnologia

Para os exercícios 61-65, use sua calculadora para representar graficamente a função polinomial. Com base no gráfico, encontre os zeros racionais. Todas as soluções reais são racionais.

61)\(f(x)=6x^3−7x^2+1\)

Responda

\(1, \dfrac{1}{2}, −\dfrac{1}{3}\)

62)\(f(x)=4x^3−4x^2−13x−5\)

63)\(f(x)=8x^3−6x^2−23x+6\)

Responda

\(2, \dfrac{1}{4}, −\dfrac{3}{2}\)

64)\(f(x)=12x^4+55x^3+12x^2−117x+54\)

65)\(f(x)=16x^4−24x^3+x^2−15x+25\)

Responda

\(\dfrac{5}{4}\)

Extensões

Para os exercícios 66-70, construa uma função polinomial do menor grau possível usando as informações fornecidas.

66) Raízes reais:\(–1, 1, 3\) e\((2,f(2))=(2,4)\)

67) Raízes reais:\(–1\) (com multiplicidade\(2\) e\(1\)) e\((2,f(2))=(2,4)\)

Responda

\(f(x)=\dfrac{4}{9}(x^3+x^2−x−1)\)

68) Raízes reais:\(–2, \dfrac{1}{2}\) (com multiplicidade\(2\)) e\((−3,f(−3))=(−3,5)\)

69) Raízes reais:\(−\dfrac{1}{2}, 0,\dfrac{1}{2}\) e\((−2,f(−2))=(−2,6)\)

Responda

\(f(x)=−\dfrac{1}{5}(4x^3−x)\)

70) Raízes reais:\(–4, –1, 1, 4\) e\((−2,f(−2))=(−2,10)\)

Aplicativos do mundo real

Para os exercícios 71-75, encontre as dimensões da caixa descrita.

71) O comprimento é duas vezes maior que a largura. A altura é\(2\) polegadas maior que a largura. O volume é em polegadas\(192\) cúbicas.

Responda

\(8\)\(4\)por\(6\) polegadas

72) O comprimento, a largura e a altura são números inteiros consecutivos. O volume é em polegadas\(120 \) cúbicas.

73) O comprimento é uma polegada a mais que a largura, que é uma polegada a mais que a altura. O volume é em polegadas\(86.625\) cúbicas.

Responda

\(5.5\)\(4.5\)por\(3.5\) polegadas

74) O comprimento é três vezes a altura e a altura é uma polegada menor que a largura. O volume é em polegadas\(108\) cúbicas.

75) O comprimento é\(3\) polegadas a mais do que a largura. A largura é\(2\) polegadas a mais do que a altura. O volume é em polegadas\(120\) cúbicas.

Responda

\(8\)\(5\)por\(3\) polegadas

Para os exercícios 76-80, encontre as dimensões do cilindro circular direito descrito.

76) O raio é\(3\) polegadas a mais do que a altura. O volume é de metros\(16π\) cúbicos.

77) A altura é um a menos da metade do raio. O volume é de metros\(72π\) cúbicos.

Responda

Raio =\(6\) metros, Altura =\(2\) metros

78) O raio e a altura diferem em um metro. O raio é maior e o volume é em metros\(48π\) cúbicos.

79) O raio e a altura diferem em dois metros. A altura é maior e o volume é em metros\(28.125π\) cúbicos.

Responda

Raio =\(2.5\) metros, Altura =\(4.5\) metros

80) O raio é um\(\dfrac{1}{3}\) metro maior que a altura. O volume é de metros\(\dfrac{98}{9}π\) cúbicos.

3.7 Funções racionais

Verbal

1) Qual é a diferença fundamental na representação algébrica de uma função polinomial e uma função racional?

Responda

A função racional será representada por um quociente de funções polinomiais.

2) Qual é a diferença fundamental nos gráficos das funções polinomiais e das funções racionais?

3) Se o gráfico de uma função racional tiver uma descontinuidade removível, o que deve ser verdade com a regra funcional?

Responda

O numerador e o denominador devem ter um fator comum.

4) Um gráfico de uma função racional não pode ter assíntota vertical? Em caso afirmativo, como?

5) Um gráfico de uma função racional não pode ter interceptos x? Em caso afirmativo, como?

Responda

Sim. O numerador da fórmula das funções teria apenas raízes complexas e/ou fatores comuns ao numerador e ao denominador.

Algébrico

Para os exercícios 6-9, encontre o domínio das funções racionais.

6)\(f(x)=\dfrac{x-1}{x+2}\)

7)\(f(x)=\dfrac{x+1}{x^{2}-1}\)

Responda

Todos os reais\(x \neq -1,1\)

8)\(f(x)=\dfrac{x^{2}+4}{x^{2}-2 x-8}\)

9)\(f(x)=\dfrac{x^{2}+4 x-3}{x^{4}-5 x^{2}+4}\)

Responda

Todos os reais\(x \neq-1,-2,1,2\)

Para os exercícios 10-19, encontre o domínio, as assíntotas verticais e as assíntotas horizontais das funções.

10)\(f(x)=\dfrac{4}{x-1}\)

11)\(f(x)=\dfrac{2}{5 x+2}\)

Responda

V.A. em\(x=-\dfrac{2}{5}\); H.A. em\(y=0\); O domínio é tudo real\(x \neq-\dfrac{2}{5}\)

12)\(f(x)=\dfrac{x}{x^{2}-9}\)

13)\(f(x)=\dfrac{x}{x^{2}+5 x-36}\)

Responda

V.A. em\(x=4,-9\); H.A. em\(y=0\); O domínio é tudo real\(x \neq 4,-9\)

14)\(f(x)=\dfrac{3+x}{x^{3}-27}\)

15)\(f(x)=\dfrac{3x-4}{x^{3}-16x}\)

Responda

V.A. em\(x=0,4,-4\); H.A. em\(y=0\); O domínio é tudo real\(x \neq 0,4,-4\)

16)\(f(x)=\dfrac{x^{2}-1}{x^{3}+9 x^{2}+14 x}\)

17)\(f(x)=\dfrac{x+5}{x^{2}-25}\)

Responda

V.A. em\(x=-5\); H.A. em\(y=0\); O domínio é tudo real\(x \neq 5,-5\)

18)\(f(x)=\dfrac{x-4}{x-6}\)

19)\(f(x)=\dfrac{4-2x}{3 x-1}\)

Responda

V.A. em\(x=\dfrac{1}{3}\); H.A. em\(y=-\dfrac{2}{3}\); O domínio é tudo real\(x \neq \dfrac{1}{3}\)

Para os exercícios 20-24, encontre os\(y\) interceptos\(x\) - e -para as funções.

20)\(f(x)=\dfrac{x+5}{x^{2}+4}\)

21)\(f(x)=\dfrac{x}{x^{2}-x}\)

Responda

nenhum

22)\(f(x)=\dfrac{x^{2}+8 x+7}{x^{2}+11 x+30}\)

23)\(f(x)=\dfrac{x^{2}+x+6}{x^{2}-10 x+24}\)

Responda

\(x\)-intercepta nenhum,\(y\) -intercepta\(\left(0, \dfrac{1}{4}\right)\)

24)\(f(x)=\dfrac{94-2 x^{2}}{3 x^{2}-12}\)

Para os exercícios 25-29, descreva o comportamento local e final das funções.

25)\(f(x)=\dfrac{x}{2 x+1}\)

Responda

Comportamento local:\(x \rightarrow-\dfrac{1}{2}^{+}, f(x) \rightarrow-\infty, x \rightarrow-\dfrac{1}{2}^{-}, f(x) \rightarrow \infty\)

Comportamento final:\(x \rightarrow \pm \infty, f(x) \rightarrow \dfrac{1}{2}\)

26)\(f(x)=\dfrac{2x}{x-6}\)

27)\(f(x)=\dfrac{-2x}{x-6}\)

Responda

Comportamento local:\(x \rightarrow 6^{+}, f(x) \rightarrow-\infty, x \rightarrow 6^{-}, f(x) \rightarrow \infty \)

Comportamento final:\(x \rightarrow \pm \infty, f(x) \rightarrow-2\)

28)\(f(x)=\dfrac{x^{2}-4 x+3}{x^{2}-4x-5}\)

29)\(f(x)=\dfrac{2 x^{2}-32}{6 x^{2}+13x-5}\)

Responda

Comportamento local:\(x \rightarrow-\dfrac{1}{3}, f(x) \rightarrow \infty, x \rightarrow-\dfrac{1}{3}, f(x) \rightarrow-\infty, x \rightarrow \dfrac{5}{2}, f(x) \rightarrow \infty, x \rightarrow \dfrac{5}{2}+f(x) \rightarrow-\infty\)

Comportamento final:\(x \rightarrow \pm \infty, f(x) \rightarrow \dfrac{1}{3}\)

Para os exercícios 30-34, encontre a assíntota inclinada das funções.

30)\(f(x)=\dfrac{24 x^{2}+6 x}{2 x+1}\)

31)\(f(x)=\dfrac{4 x^{2}-10}{2 x-4}\)

Responda

\(y=2 x+4\)

32)\(f(x)=\dfrac{81 x^{2}-18}{3 x-2}\)

33)\(f(x)=\dfrac{6 x^{3}-5 x}{3 x^{2}+4}\)

Responda

\(y=2 x\)

34)\(f(x)=\dfrac{x^{2}+5x+4}{x-1}\)

Gráfica

Para os exercícios 35-38, use a transformação dada para representar graficamente a função. Observe as assíntotas verticais e horizontais.

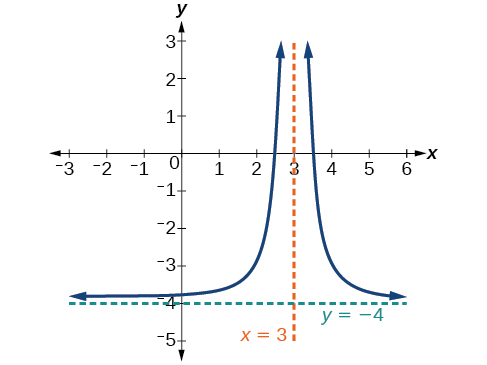
35) A função recíproca aumentou duas unidades.

Responda

V.A.\(x=0\), H.A.\(y=2\)

36) A função recíproca desceu uma unidade e deixou três unidades.

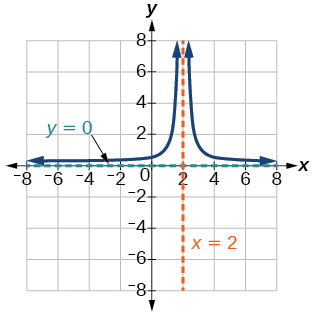
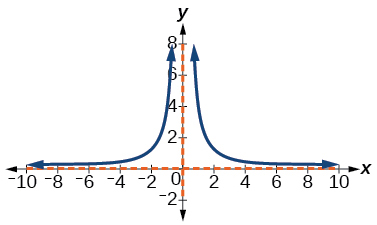
37) A função quadrada recíproca foi deslocada para as\(2\) unidades corretas.

Responda

V.A.\(x=2\), H.A.\(y=0\)

38) A função quadrada recíproca foi deslocada para baixo em\(2\) unidades e\(1\) unidade direita.

Para os exercícios 39-50, encontre as interceptações horizontais, a interceptação vertical, as assíntotas verticais e a assíntota horizontal ou inclinada das funções. Use essas informações para esboçar um gráfico.

39)\(p(x)=\dfrac{2x-3}{x+4}\)

Responda

V.A.\(x=-4\), H.A.\(y=2\)\(\left(\dfrac{3}{2}, 0\right)\);\(\left(0,-\dfrac{3}{4}\right)\)

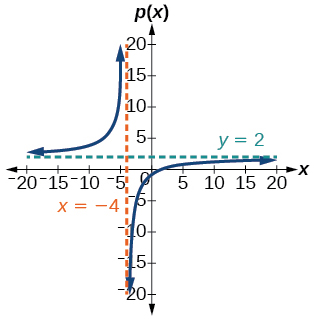
40)\(q(x)=\dfrac{x-5}{3 x-1}\)

41)\(s(x)=\dfrac{4}{(x-2)^{2}}\)

Responda

V.A.\(x=2\), H.A.\(y=0\),\((0,1)\)

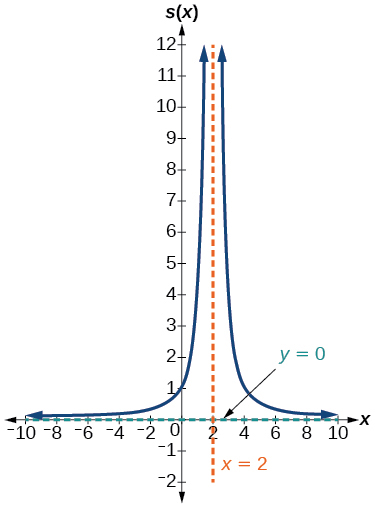
(42)\(r(x)=\dfrac{5}{(x+1)^{2}}\)

43)\(f(x)=\dfrac{3 x^{2}-14 x-5}{3 x^{2}+8 x-16}\)

Responda

V.A.\(x=-4\)\(x=\dfrac{4}{3}\), H.A.\(y=1\);\((5,0)\);\(\left(-\dfrac{1}{3}, 0\right)\);\(\left(0, \dfrac{5}{16}\right)\)

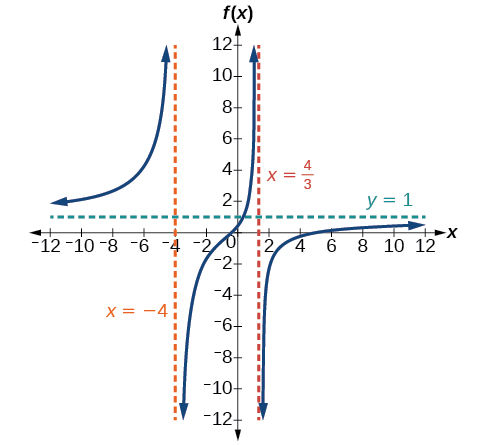
44)\(g(x)=\dfrac{2 x^{2}+7 x-15}{3 x^{2}-14+15}\)

45)\(a(x)=\dfrac{x^{2}+2 x-3}{x^{2}-1}\)

Responda

V.A.\(x=−1\), H.A.\(y=1\)\((−3,0)\);\((0,3)\)

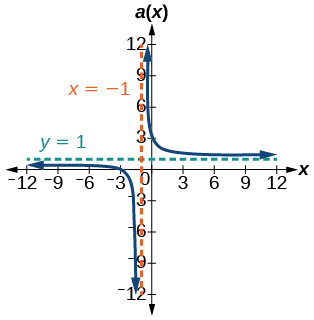
(46)\(b(x)=\dfrac{x^{2}-x-6}{x^{2}-4}\)

47)\(h(x)=\dfrac{2 x^{2}+x-1}{x-4}\)

Responda

V.A.\(x=4\), S.A.\(y=2x+9\);\((-1,0)\);\(\left(\dfrac{1}{2}, 0\right)\);\(\left(0, \dfrac{1}{4}\right)\)

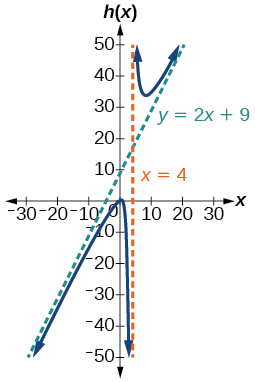
48)\(k(x)=\dfrac{2 x^{2}-3 x-20}{x-5}\)

49)\(w(x)=\dfrac{(x-1)(x+3)(x-5)}{(x+2)^{2}(x-4)}\)

Responda

V.A.\(x=-2\)\(x=4\), H.A.\(y=1\),\((1,0)\);\((5,0)\);\((-3,0)\);\(\left(0,-\dfrac{15}{16}\right)\)

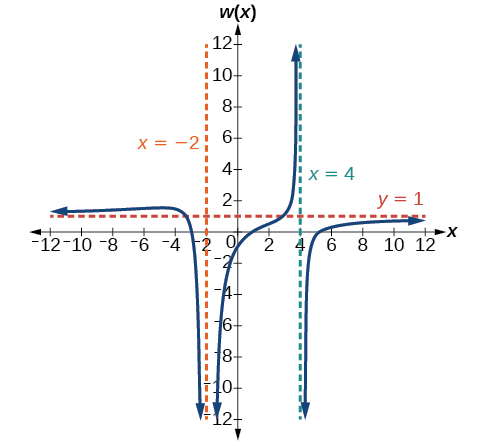
50)\(z(x)=\dfrac{(x+2)^{2}(x-5)}{(x-3)(x+1)(x+4)}\)

Para os exercícios 51-56, escreva uma equação para uma função racional com as características dadas.

51) Assíntotas verticais em\(x=5\),\(x\) -intercepta em\((2,0)\) e\((-1,0), y\) -interceptam em\((0,4)\)

Resposta

\(y=50 \dfrac{x^{2}-x-2}{x^{2}-25}\)

52) Assíntotas verticais em\(x=-4\) e\(x=-1, x\) -intercepta em\((1,0)\) e\((5,0), y\) -interceptam em\((0,7)\)

53) Assíntotas verticais em\(x=-4\) e\(x=-5, x\) -intercepta em\((4,0)\) e assíntota\((-6,0),\) horizontal em\(y=7\)

Resposta

\(y=7 \dfrac{x^{2}+2 x-24}{x^{2}+9 x+20}\)

54) Assíntotas verticais em\(x=-3\) e\(x=6, x\) -intercepta em\((-2,0)\) e assíntota\((1,0),\) horizontal em\(y=-2\)

55) Assíntota vertical em zero\(x=-1,\) duplo em\(x=2, y\) -intercepto em\((0,2)\)

Resposta

\(y=\dfrac{1}{2} \dfrac{x^{2}-4 x+4}{x+1}\)

56) Assíntota vertical em zero\(x=3,\) duplo em\(x=1, y\) -intercepto em\((0,4)\)

Para os exercícios 57-,64, use os gráficos para escrever uma equação para a função.

57)

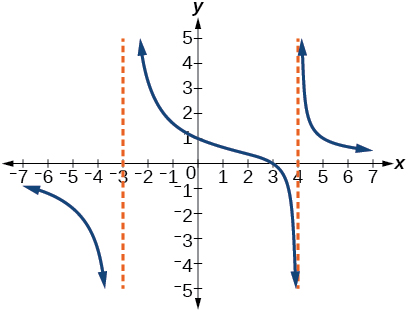
Resposta

\(y=4 \dfrac{x-3}{x^{2}-x-12}\)

(58)

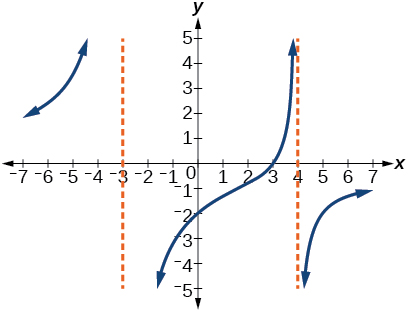
59)

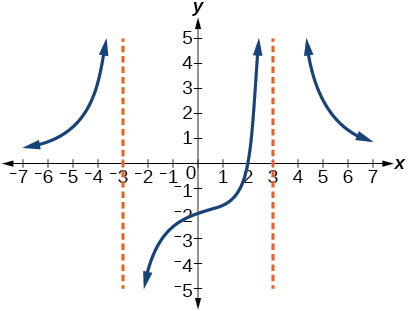
Resposta

\(y=-9 \dfrac{x-2}{x^{2}-9}\)

60)

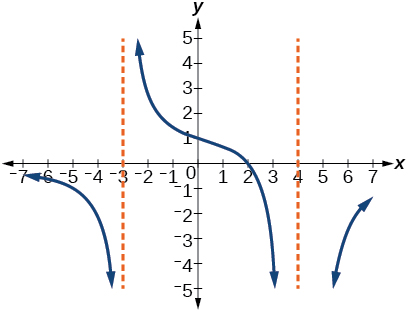
61)

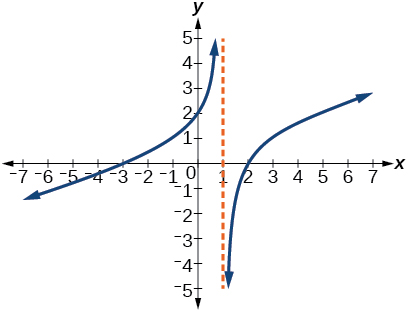
Resposta

\(y=\dfrac{1}{3} \dfrac{x^{2}+x-6}{x-1}\)

62)

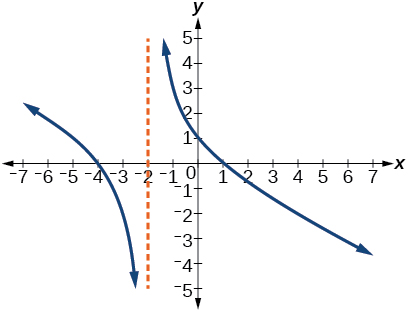
63)

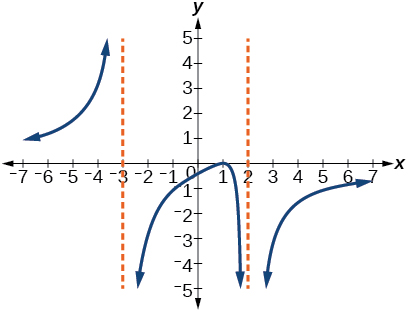
Resposta

\(y=-6 \dfrac{(x-1)^{2}}{(x+3)(x-2)^{2}}\)

64)

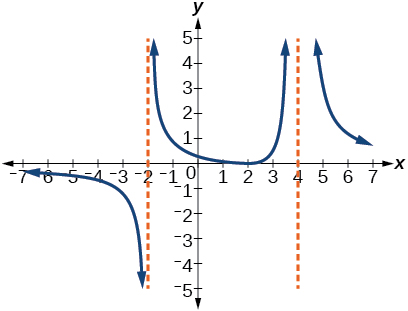
Numérico

Para os exercícios 65-69, faça tabelas para mostrar o comportamento da função próxima à assíntota vertical e refletindo a assíntota horizontal

65)\(f(x)=\dfrac{1}{x-2}\)

Resposta

\(x\)	2,01	2.001	2.0001	1,99	1.999
\ (x\) ">\(y\)	100	1.000	10.000	—100	—1.000

\(x\)	10	100	1.000	10.000	100.000
\ (x\) ">\(y\)	1.25	.0102	.001	0,001	0,00001

Assíntota vertical\(x=2\), assíntota horizontal\(y=0\)

66)\(f(x)=\dfrac{x}{x-3}\)

67)\(f(x)=\dfrac{2x}{x+4}\)

Resposta

\(x\)	—4,1	—4,01	—4.001	—3,99	—3,99
\ (x\) ">\(y\)	82	802	8.002	—798	—7998

\(x\)	10	100	1.000	10.000	100.000
\ (x\) ">\(y\)	1.4286	1.9331	1.992	1.992	1,999992

Assíntota vertical\(x=-4\), assíntota horizontal\(y=2\)

68)\(f(x)=\dfrac{2 x}{(x-3)^{2}}\)

69)\(f(x)=\dfrac{x^{2}}{x^{2}+2 x+1}\)

Resposta

\(x\)	—.9	—.99	—.999	—1,1	—1,01
\ (x\) ">\(y\)	81	9.801	998.001	121	10.201

\(x\)	10	100	1.000	10.000	100.000
\ (x\) ">\(y\)	82645	.9803	.998	.9998

Assíntota vertical\(x=-1\), Assíntota horizontal\(y=1\)

Tecnologia

Para os exercícios 70-74, use uma calculadora para representar graficamente\(f(x)\). Use o gráfico para resolver \(f(x)>0\).

70)\(f(x)=\dfrac{2}{x+1}\)

71)\(f(x)=\dfrac{4}{2x-3}\)

Resposta

\(\left(\dfrac{3}{2}, \infty\right)\)

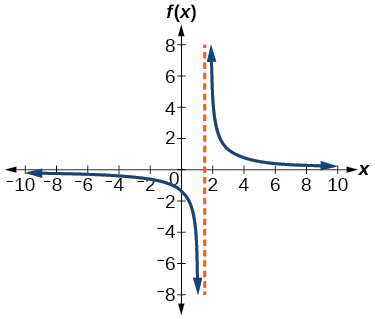
72)\(f(x)=\dfrac{2}{(x-1)(x+2)}\)

73)\(f(x)=\dfrac{x+2}{(x-1)(x-4)}\)

Resposta

\((-2,1) \cup(4, \infty)\)

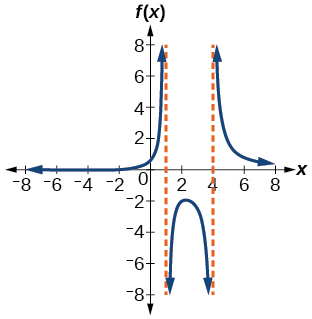
74)\(f(x)=\dfrac{(x+3)^{2}}{(x-1)^{2}(x+1)}\)

Extensões

Para os exercícios 75-79, identifique a descontinuidade removível.

75)\(f(x)=\dfrac{x^{2}-4}{x-2}\)

Resposta

\((2,4)\)

76)\(f(x)=\dfrac{x^{3}+1}{x+1}\)

77)\(f(x)=\dfrac{x^{2}+x-6}{x-2}\)

Resposta

\((2,5)\)

78)\(f(x)=\dfrac{2 x^{2}+5 x-3}{x+3}\)

79)\(f(x)=\dfrac{x^{3}+x^{2}}{x+1}\)

Resposta

\((-1,1)\)

Aplicativos do mundo real

Para os exercícios 80-81, expresse uma função racional que descreva a situação.

80) Um grande tanque de mistura atualmente contém\(200\) galões de água, nos quais\(10\) libras de açúcar foram misturadas. Uma torneira se abrirá, despejando\(10\) galões de água por minuto no tanque ao mesmo tempo em que o açúcar é despejado no tanque a uma taxa de\(3\) libras por minuto. Encontre a concentração (libras por galão) de açúcar no tanque depois\(t\) minutos.

81) Um grande tanque de mistura atualmente contém\(300\) galões de água, nos quais\(8\) libras de açúcar foram misturadas. Uma torneira se abrirá, despejando\(20\) galões de água por minuto no tanque ao mesmo tempo em que o açúcar é despejado no tanque a uma taxa de\(2\) libras por minuto. Encontre a concentração (libras por galão) de açúcar no tanque após\(t\) alguns minutos.

Resposta

\(C(t)=\dfrac{8+2t}{300+20t}\)

Para os exercícios 82-83, use a função racional dada para responder à pergunta.

82) A concentração\(C\) de um medicamento na corrente sanguínea de um paciente\(t\) horas após a injeção é administrada por\(C(t)=\dfrac{2t}{3+t^{2}}\). O que acontece com a concentração do medicamento à medida que\(t\) aumenta?

83) A concentração\(C\) de um medicamento na corrente sanguínea de um paciente, horas após a injeção, é administrada por\(C(t)=\dfrac{100t}{2 t^{2}+75}\). Use uma calculadora para aproximar o momento em que a concentração é mais alta.

Resposta

Depois de cerca\(6.12\) de horas.

Para os exercícios 84-88, construa uma função racional que ajudará a resolver o problema. Em seguida, use uma calculadora para responder à pergunta.

84) Uma caixa aberta com base quadrada deve ter um volume de polegadas\(108\) cúbicas. Encontre as dimensões da caixa que terá uma área de superfície mínima. Seja\(x\) = comprimento do lado da base.

85) Uma caixa retangular com base quadrada deve ter um volume de pés\(20\) cúbicos. O material para a base custa\(30\) centavos/pé quadrado. O material para os lados custa\(10\) centavos/pé quadrado. O material para o topo custa\(20\) centavos/pé quadrado. Determine as dimensões que produzirão um custo mínimo. Seja\(x\) = comprimento do lado da base.

Resposta

\(A(x)=50 x^{2}+\dfrac{800}{x} \cdot 2\)\(2\)pelos\(5\) pés.

86) Um cilindro circular reto tem um volume de polegadas\(100\) cúbicas. Encontre o raio e a altura que produzirão uma área de superfície mínima. Seja\(x\) = raio.

87) Um cilindro circular reto sem topo tem um volume de metros\(50\) cúbicos. Encontre o raio que produzirá a área de superfície mínima. Seja\(x\) = raio.

Resposta

\(A(x)=\pi x^{2}+\dfrac{100}{x}\). Raio =\(2.52\) metros.

88) Um cilindro circular reto deve ter um volume de polegadas\(40\) cúbicas. Custa\(4\) centavos/polegada quadrada para construir a parte superior e inferior e\(1\) centavos/polegada quadrada para construir o resto do cilindro. Encontre o raio para obter o custo mínimo. Seja\(x\) = raio.

3.8 Funções inversas e radicais

Verbal

1) Explique por que não podemos encontrar funções inversas para todas as funções polinomiais.

Resposta

Pode ser muito difícil ou impossível de resolver. em termos de\(y\).

2) Por que devemos restringir o domínio de uma função quadrática ao encontrar seu inverso?

3) Ao encontrar o inverso de uma função radical, que restrição precisaremos fazer?

Resposta

Precisaremos de uma restrição no domínio da resposta.

4) O inverso de uma função quadrática sempre assumirá qual forma?

Algébrico

Para os exercícios 5-12, encontre o inverso da função no domínio dado.

5)\(f(x)=(x-4)^{2},[4, \infty)\)

Resposta

\(f^{-1}(x)=\sqrt{x}+4\)

6)\(f(x)=(x+2)^{2},[-2, \infty)\)

7)\(f(x)=(x+1)^{2}-3,[-1, \infty)\)

Resposta

\(f^{-1}(x)=\sqrt{x+3}-1\)

8)\(f(x)=2-\sqrt{3+x}\)

9)\(f(x)=3 x^{2}+5,(-\infty, 0]\)

Resposta

\(f^{-1}(x)=-\sqrt{\dfrac{x-5}{3}}\)

10)\(f(x)=12-x^{2},[0, \infty)\)

11)\(f(x)=9-x^{2},[0, \infty)\)

Resposta

\(f(x)=\sqrt{9-x}\)

12)\(f(x)=2 x^{2}+4,[0, \infty)\)

Para os exercícios 13-16, determine o inverso das funções.

13)\(f(x)=x^{3}+5\)

Resposta

\(f^{-1}(x)=\sqrt[3]{x-5}\)

14)\(f(x)=3 x^{3}+1\)

15)\(f(x)=4-x^{3}\)

Resposta

\(f^{-1}(x)=\sqrt[3]{4-x}\)

16)\(f(x)=4-2 x^{3}\)

Para os exercícios 17-31, determine o inverso das funções.

17)\(f(x)=\sqrt{2x+1}\)

Resposta

\(f^{-1}(x)=\dfrac{x^{2}-1}{2},[0, \infty)\)

18)\(f(x)=\sqrt{3-4x}\)

19)\(f(x)=9+\sqrt{4x-4}\)

Resposta

\(f^{-1}(x)=\dfrac{(x-9)^{2}+4}{4},[9, \infty)\)

20)\(f(x)=\sqrt{6x-8}+5\)

21)\(f(x)=9+2 \sqrt[3]{x}\)

Resposta

\(f^{-1}(x)=\left(\dfrac{x-9}{2}\right)^{3}\)

22)\(f(x)=3-\sqrt[3]{x}\)

23)\(f(x)=\dfrac{2}{x+8}\)

Resposta

\(f^{-1}(x)=\dfrac{2-8x}{x}\)

24)\(f(x)=\dfrac{3}{x-4}\)

25)\(f(x)=\dfrac{x+3}{x+7}\)

Resposta

\(f^{-1}(x)=\dfrac{7x-3}{1-x}\)

26)\(f(x)=\dfrac{x-2}{x+7}\)

27)\(f(x)=\dfrac{3x+4}{5}\)

Resposta

\(f^{-1}(x)=\dfrac{5x-4}{4x+3}\)

28)\(f(x)=\dfrac{5x+1}{2-5x}\)

29)\(f(x)=x^{2}+2 x,[-1, \infty)\)

Resposta

\(f^{-1}(x)=\sqrt{x+1}-1\)

30)\(f(x)=x^{2}+4 x+1,[-2, \infty)\)

31)\(f(x)=x^{2}-6 x+3,[3, \infty)\)

Resposta

\(f^{-1}(x)=\sqrt{x+6}+3\)

Gráfica

Para os exercícios 32-41, encontre o inverso da função e represente graficamente a função e seu inverso.

32)\(f(x)=x^{2}+2, x \geq 0\)

33)\(f(x)=4-x^{2}, x \geq 0\)

Resposta

\(f^{-1}(x)=\sqrt{4-x}\)

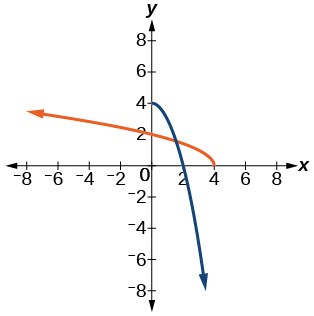
34)\(f(x)=(x+3)^{2}, x \geq-3\)

(35)\(f(x)=(x-4)^{2}, x \geq 4\)

Resposta

\(f^{-1}(x)=\sqrt{x}+4\)

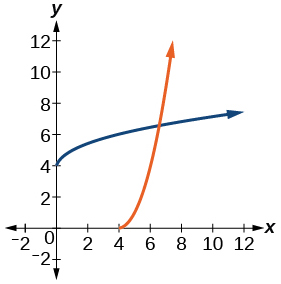
36)\(f(x)=x^{3}+3\)

37)\(f(x)=1-x^{3}\)

Resposta

\(f^{-1}(x)=\sqrt[3]{1-x}\)

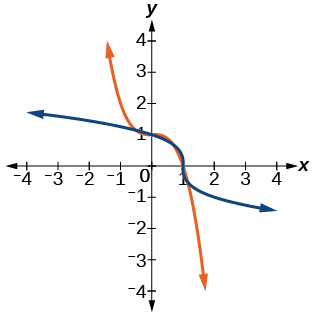
38)\(f(x)=x^{2}+4 x, x \geq-2\)

39)\(f(x)=x^{2}-6 x+1, x \geq 3\)

Resposta

\(f^{-1}(x)=\sqrt{x+8}+3\)

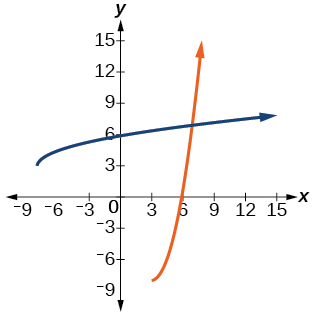
40)\(f(x)=\dfrac{2}{x}\)

41)\(f(x)=\dfrac{1}{x^{2}}, x \geq 0\)

Resposta

\(f^{-1}(x)=\sqrt{\dfrac{1}{x}}\)

Para os exercícios 42-46, use um gráfico para ajudar a determinar o domínio das funções.

(42)\(f(x)=\sqrt{\dfrac{(x+1)(x-1)}{x}}\)

43)\(f(x)=\sqrt{\dfrac{(x+2)(x-3)}{x-1}}\)

Resposta

\([-2,1) \cup[3, \infty)\)

44)\(f(x)=\sqrt{\dfrac{x(x+3)}{x-4}}\)

45)\(f(x)=\sqrt{\dfrac{x^{2}-x-20}{x-2}}\)

Resposta

\([-4,2) \cup[5, \infty)\)

(46)\(f(x)=\sqrt{\dfrac{9 x^{2}}{x+4}}\)

Tecnologia

Para os exercícios 47-51, use uma calculadora para representar graficamente a função. Em seguida, usando o gráfico, forneça três pontos no gráfico do inverso com\(y\) coordenadas -dadas.

47)\(f(x)=x^{3}-x-2, y=1,2,3\)

Resposta

\((-2,0) ;(4,2) ;(22,3)\)

48)\(f(x)=x^{3}+x-2, y=0,1,2\)

49)\(f(x)=x^{3}+3 x-4, y=0,1,2\)

Resposta

\((-4,0) ;(0,1) ;(10,2)\)

50)\(f(x)=x^{3}+8 x-4, y=-1,0,1\)

51)\(f(x)=x^{4}+5 x+1, y=-1,0,1\)

Resposta

\((-3,-1) ;(1,0) ;(7,1)\)

Extensões

Para os exercícios 52-56, determine o inverso das funções com números reais\(a, b, c\) positivos.

52)\(f(x)=ax^{3}+b\)

53)\(f(x)=x^{2}+bx\)

Resposta

\(f^{-1}(x)=\sqrt{x+\dfrac{b^{2}}{4}}-\dfrac{b}{2}\)

54)\(f(x)=\sqrt{a x^{2}+b}\)

55)\(f(x)=\sqrt[3]{a x+b}\)

Resposta

\(f^{-1}(x)=\dfrac{x^{2}-b}{a}\)

56)\(f(x)=\dfrac{ax+b}{x+c}\)

Aplicativos do mundo real

Para os exercícios 57-66, determine a função descrita e use-a para responder à pergunta.

57) Um objeto caído de uma altura de\(200\) metros tem uma altura,\(h(t)\), em metros após o decorrer de\(t\) segundos, tal que\(h(t)=200-4.9 t^{2}\). \(t\)Expresse em função da altura e encontre o tempo para atingir uma altura de\(50\) metros.\(h\)

Resposta

\(t(h)=\sqrt{\dfrac{200-h}{4.9}}\),\(5.53\) segundos

58) Um objeto caído de uma altura de\(600\) pés tem uma altura,\(h(t),\) em pés após\(t\) segundos, tal que\(h(t)=600-16 t^{2}\). \(t\)Expresse em função da altura\(h\) e encontre tempo para atingir uma altura de\(400\) pés.

59) O volume,\(V\), de uma esfera em termos de seu raio,\(r\), é dado por\(V(r)=\frac{4}{3} \pi r^{3}\). \(r\)Expresse em função de\(V\) e encontre o raio de uma esfera com volume de pés\(200\) cúbicos.

Resposta

\(r(V)=\sqrt[3]{\dfrac{3 V}{4 \pi}}\),\(3.63\) pés

60) A área da superfície\(A\),, de uma esfera em termos de seu raio,\(r\), é dada por\(A(r)=4 \pi r^{2}\). \(r\)Expresse em função de\(V\) e encontre o raio de uma esfera com uma área de superfície de polegadas\(1000\) quadradas.

61) Um recipiente contém\(100\) ml de uma solução que é\(25\) ml de ácido. Se\(n\) ml de uma solução que é\(60\%\) ácida for adicionado, a função\(C(n)=\dfrac{25+.6 n}{100+n}\) fornece a concentração\(C\),, em função do número de ml adicionados,\(n\). \(n\)Expresse em função de\(C\) e determine o número de mL que precisam ser adicionados para ter uma solução\(50\%\) ácida.

Responda

\(n(C)=\dfrac{100 C-25}{6-C}, 250 \mathrm{mL}\)

62) O período\(T\), em segundos, de um pêndulo simples em função de seu comprimento\(l\), em pés, é dado por\(T(l)=2 \pi \sqrt{\dfrac{l}{322}}\). \(l\)Expresse em função de\(T\) e determine o comprimento de um pêndulo com período de\(2\) segundos.

63) O volume de um cilindro\(V\), em termos de raio e altura,\(h\), é dado por\(V=\pi r^{2} h\).\(r\) Se um cilindro tiver uma altura de\(6\) metros, expresse o raio em função de\(V\) e encontre o raio de um cilindro com volume de metros\(300\) cúbicos.

Responda

\(r(V)=\sqrt{\dfrac{V}{6 \pi}}, 3.99\)metros

64) A área da superfície,\(A\), de um cilindro em termos de seu raio\(r\),, e altura,\(h\), é dada por\(A=2 \pi r^{2}+2 \pi r h\). Se a altura do cilindro for\(4\) pés, expresse o raio em função de\(V\) e encontre o raio se a área da superfície for pés\(200\) quadrados.

65) O volume de um cone circular reto\(V\), em termos de seu raio\(r\), e sua altura,\(h\), é dado por\(V=\frac{1}{3} \pi r^{2} h\). \(r\)\(V\)Expresse se a altura do cone é\(12\) pés e encontre o raio de um cone com volume de polegadas\(50\) cúbicas.

Responda

\(r(V)=\sqrt{\dfrac{V}{4 \pi}}, 1.99\)polegadas

66) Considere um cone com altura de\(30\) pés. Expresse o raio\(r\), em termos de volume,\(V\), e encontre o raio de um cone com volume de pés\(1000\) cúbicos.

3.9 Modelagem usando variação

Verbal

1) O que é verdade sobre a aparência de gráficos que refletem uma variação direta entre duas variáveis?

Responda

O gráfico terá a aparência de uma função de potência.

2) Se duas variáveis variarem inversamente, como será uma equação representando seu relacionamento?

3) Existe um limite para o número de variáveis que podem variar em conjunto? Explique.

Responda

Não. Várias variáveis podem variar em conjunto.

Algébrico

Para os exercícios 4-23, escreva uma equação descrevendo a relação das variáveis dadas.

4)\(y\) varia diretamente à medida que\(x\) e quando\(x=6, y=12\)

5)\(y\) varia diretamente como o quadrado de\(x\) e quando\(x=4, y=80\)

Responda

\(y=5 x^{2}\)

6)\(y\) varia diretamente como a raiz quadrada de\(x\) e quando\(x=36, y=24\)

7)\(y\) varia diretamente como o cubo de\(x\) e quando\(x=36, y=24\)

Responda

\(y=10 x^{3}\)

8)\(y\) varia diretamente como a raiz cúbica de\(x\) e quando\(x=27, y=15\)

9)\(y\) varia diretamente como a quarta potência de\(x\) e quando\(x=1, y=6\)

Responda

\(y=6 x^{4}\)

10)\(y\) varia inversamente à medida que\(x\) e quando\(x=4, y=2\)

11)\(y\) varia inversamente como o quadrado de\(x\) e quando\(x=3, y=2\)

Responda

\(y=\dfrac{18}{x^{2}}\)

12)\(y\) varia inversamente como o cubo de\(x\) e quando\(x=2, y=5\)

13)\(y\) varia inversamente como a quarta potência de\(x\) e quando\(x=3, y=1\)

Responda

\(y=\dfrac{81}{x^{4}}\)

14)\(y\) varia inversamente como a raiz quadrada de\(x\) e quando\(x=25, y=3\)

15)\(y\) varia inversamente como a raiz cúbica de\(x\) e quando\(x=64, y=5\)

Responda

\(y=\dfrac{20}{\sqrt[3]{x}}\)

16)\(y\) varia em conjunto com\(x\)\(z\) e quando\(x=2\) e\(z=3, y=36\)

17)\(y\) varia conjuntamente como\(x, z,\)\(w\) e quando\(x=1, z=2, w=5\), então\(y=100\)

Responda

\(y=10 x z w\)

18)\(y\) varia conjuntamente como o quadrado de\(x\) e o quadrado de\(z\) e quando\(x=3\) e\(z=4\), então\(y=72\)

19)\(y\) varia conjuntamente como\(x\) e a raiz quadrada de\(z\) e quando\(x=2\) e\(z=25\), então\(y=100\)

Responda

\(y=10 x \sqrt{z}\)

20)\(y\) varia conjuntamente como o quadrado\(x\) do cubo de\(z\) e a raiz quadrada de\(w .\) Quando\(x=1, z=2,\) e\(w=36,\) então\(y=48\)

21)\(y\) varia conjuntamente como\(x\)\(z\) e inversamente como\(w\). Quando\(x=3, z=5,\) e\(w=6,\) depois\(y=10\)

Responda

\(y=4 \dfrac{x z}{w}\)

22)\(y\) varia conjuntamente como o quadrado de\(x\) e a raiz quadrada de\(z\) e inversamente como o cubo de\(w\). Quando e\(x=3, z=4\)\(w=3\), então\(y=6\)

23)\(y\) varia conjuntamente como\(x\)\(z\) e inversamente como a raiz quadrada de e o quadrado de\(t\). Quando e\(x=3, z=1, w=25\)\(t=2\), então\(y=6\)

Responda

\(y=40 \dfrac{x z}{\sqrt{w} t^{2}}\)

Numérico

Para os exercícios 24-40, use as informações fornecidas para encontrar o valor desconhecido.

24)\(y\) varia diretamente como\(x\). \(x=3,\)Então, quando\(y=12\). Descubra\(y\) quando\(x=20\).

25)\(y\) varia diretamente como o quadrado de\(x\). Quando\(x=2\), então\(y=16\). Descubra\(y\) quando\(x=8\).

Responda

\(y=256\)

26)\(y\) varia diretamente como o cubo de\(x\). Quando\(x=3\), então\(y=5\). Descubra\(y\) quando\(x=4\).

27)\(y\) varia diretamente como a raiz quadrada de\(x\). Quando\(x=16\), então\(y=4\). Descubra\(y\) quando\(x=36\).

Responda

\(y=6\)

28)\(y\) varia diretamente como a raiz cúbica de\(x\). Quando\(x=125\), então\(y=15\). Descubra\(y\) quando\(x=1,000\).

29)\(y\) varia inversamente com\(x\). Quando\(x=3\), então\(y=2\). Descubra\(y\) quando\(x=1\).

Responda

\(y=6\)

30)\(y\) varia inversamente com o quadrado de\(x\). Quando\(x=4\), então\(y=3\). Descubra\(y\) quando\(x=2\).

31)\(y\) varia inversamente com o cubo de\(x\). Quando\(x=3\), então\(y=1\). Descubra\(y\) quando\(x=1\).

Responda

\(y=27\)

32)\(y\) varia inversamente com a raiz quadrada de\(x\). Quando\(x=64\), então\(y=12\). Descubra\(y\) quando\(x=36\).

33)\(y\) varia inversamente com a raiz cúbica de\(x\). Quando\(x=27\), então\(y=5\). Descubra\(y\) quando\(x=125\).

Responda

\(y=3\)

34)\(y\) varia conjuntamente como\(x\)\(z\) e. Quando\(x=4\) e\(z=2\), então\(y=16\). Descubra\(y\) quando\(x=3\)\(z=3\) e.

35)\(y\) varia conjuntamente como\(x, z\),\(w\) e. Quando\(x=2, z=1\) e\(w=12\) depois\(y=72\). Descubra\(y\) quando\(x=1, z=2\),\(w=3\) e.

Responda

\(y=18\)

36)\(y\) varia conjuntamente como\(x\) e o quadrado de\(z\). Quando\(x=2\) e\(z=4\), então\(y=144\). Descubra\(y\) quando\(x=4\)\(z=5\) e.

37)\(y\) varia em conjunto como o quadrado de\(x\) e a raiz quadrada de\(z\). Quando\(x=9\), então\(y=24\). Descubra\(y\) quando\(x=3\)\(z=25\) e.

Responda

\(y=90\)

38)\(y\) varia conjuntamente como\(x\) e inversamente como\(w\). Quando\(x=5, z=2\) e\(w=20\) depois\(y=4\). Descubra\(y\) quando\(x=3\)\(z=8\) e\(w=48\) e.

39)\(y\) varia conjuntamente como o quadrado de\(x\) e o cubo de\(z\) e inversamente como a raiz quadrada de\(w\). Quando\(x=2, z=2\) e\(w=64\) depois\(y=12\). Descubra\(y\) quando\(x=1, z=3\),\(w=4\) e.

Responda

\(y=\dfrac{81}{2}\)

40)\(y\) varia conjuntamente como o quadrado de\(x\) e de\(z\) e inversamente como a raiz quadrada da varinha de\(t\). Quando\(x=2, z=3, w=16\) e\(t=3\) depois\(y=1\). Descubra\(y\) quando\(x=3, z=2, w=36\),\(t=5\) e.

Tecnologia

Para os exercícios 41-45, use uma calculadora para representar graficamente a equação implícita na variação dada.

41)\(y\) varia diretamente com o quadrado de\(x\) e quando\(x=2, y=3\)

Responda

\(y=\dfrac{3}{4} x^{2}\)

42)\(y\) varia diretamente como o cubo de\(x\) e quando\(x=2, y=4\).

43)\(y\) varia diretamente como a raiz quadrada de\(x\) e quando\(x=36, y=2\).

Responda

\(y=\dfrac{1}{3} \sqrt{x}\)

44)\(y\) varia inversamente com\(x\) e quando\(x=6, y=2\).

45)\(y\) varia inversamente como o quadrado de\(x\) e quando\(x=1, y=4\).

Responda

\(y=\dfrac{4}{x^{2}}\)

Extensões

Para os exercícios 46-50, use a Lei de Kepler, que afirma que o quadrado do tempo\(T\),, necessário para que um planeta orbite o Sol varia diretamente com o cubo da distância média\(a\), que o planeta está do Sol.

46) Usando a época do\(1\) ano da Terra e a distância média de 93 milhões de milhas, encontre a equação relacionada\(T\)\(a\) e.

47) Use o resultado do exercício anterior para determinar o tempo necessário para Marte orbitar o Sol se sua distância média for\(142\) de milhões de milhas.

Responda

\(1.89\)anos

48) Usando a distância da Terra de\(150\) milhões de quilômetros, encontre a equação relacionada\(T\)\(a\) e.

49) Use o resultado do exercício anterior para determinar o tempo necessário para Vênus orbitar o Sol se sua distância média for\(108\) de milhões de quilômetros.

Responda

\(0.61\)anos

50) Usando a distância da unidade\(1\) astronômica (A.U.) da Terra, determine o tempo para Saturno orbitar o Sol se sua distância média for\(9.54\) A.U.

Aplicativos do mundo real

Para os exercícios 51-60, use as informações fornecidas para responder às perguntas.

51) A distância em\(s\) que um objeto cai varia diretamente com o quadrado do tempo\(t\),, da queda. Se um objeto\(16\) cair em um segundo, por quanto tempo ele\(144\) cairá?

Responda

\(3\)segundos

52) A velocidade\(v\) de um objeto em queda varia diretamente com o tempo\(t\),, da queda. Se depois de\(2\) segundos, a velocidade do objeto for\(64\) pés por segundo, qual é a velocidade após\(5\) segundos?

53) A taxa de vibração de uma corda sob tensão constante varia inversamente com o comprimento da corda. Se uma corda tem\(24\) centímetros de comprimento e vibra\(128\) vezes por segundo, qual é o comprimento de uma corda que vibra\(64\) vezes por segundo?

Responda

\(48\)polegadas

54) O volume de um gás mantido em temperatura constante varia indiretamente com a pressão do gás. Se o volume de um gás é centímetros\(1200\) cúbicos quando a pressão é\(200\) milímetros de mercúrio, qual é o volume quando a pressão é\(300\) milímetros de mercúrio?

55) O peso de um objeto acima da superfície da Terra varia inversamente com o quadrado da distância do centro da Terra. Se um corpo pesasse\(50\) libras quando estivesse a\(3960\) milhas do centro da Terra, quanto pesaria se estivesse a\(3970\) milhas do centro da Terra?

Responda

\(49.75\)libras

56) A intensidade da luz medida em velas de pé varia inversamente com o quadrado da distância da fonte de luz. Suponha que a intensidade de uma\(0.08\) lâmpada seja de velas a uma distância de\(3\) metros. Encontre o nível de intensidade em\(8\) metros.

57) A corrente em um circuito varia inversamente com sua resistência medida em ohms. Quando a corrente em um circuito é de\(40\) amperes, a resistência é\(10\) ohms. Encontre a corrente se a resistência for\(12\) ohms.

Responda

\(33.33\)amperes

58) A força exercida pelo vento em uma superfície plana varia em conjunto com o quadrado da velocidade do vento e com a área da superfície plana. Se a área da superfície for pés\(40\) quadrados de superfície e a velocidade do vento for\(20\) milhas por hora, a força resultante será\(15\) libras. Encontre a força em uma superfície de pés\(65\) quadrados com uma velocidade de\(30\) milhas por hora.

59) A potência (hp) que um eixo pode transmitir com segurança varia junto com sua velocidade (em rotações por minuto (rpm)) e o cubo do diâmetro. Se o eixo de um determinado material com\(3\) polegadas de diâmetro pode transmitir\(45\) hp em\(100\) rpm, qual deve ser o diâmetro para transmitir\(60\) hp em\(150\) rpm?

Responda

\(2.88\)polegadas

60) A energia cinética\(K\) de um objeto em movimento varia junto com sua massa\(m\) e o quadrado de sua velocidade\(v\). Se um objeto pesando\(40\) quilogramas com uma velocidade de\(15\) metros por segundo tiver uma energia cinética de\(1000\) joules, determine a energia cinética se a velocidade for aumentada para\(20\) metros por segundo.