3.9: Modelagem usando variação

Last updated
Save as PDF

Page ID: 189217

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Nesta seção, você irá:

Resolva problemas de variação direta.
Resolva problemas de variação inversa.
Resolva problemas envolvendo variação conjunta.

Uma empresa de carros usados acaba de oferecer à sua melhor candidata, Nicole, uma posição em vendas. A posição oferece 16% de comissão sobre suas vendas. Seus ganhos dependem do valor de suas vendas. Por exemplo, se ela vender um veículo por $4.600, ela ganhará $736. Ela quer avaliar a oferta, mas não tem certeza de como. Nesta seção, analisaremos as relações, como esta, entre ganhos, vendas e taxa de comissão.

Resolvendo problemas de variação direta

No exemplo acima, os ganhos de Nicole podem ser encontrados multiplicando suas vendas por sua comissão. A fórmula nos$e=0.16s$ diz que seus ganhos vêm do produto de 0,16, sua comissão e o preço de venda do veículo.$e$ Se criarmos uma tabela, observamos que, à medida que o preço de venda aumenta, os ganhos também aumentam, o que deve ser intuitivo. Veja a Tabela 5.8.1.

$s$, preço de venda	$e=0.16s$	Interpretação
\ (s\), preço de venda” class="lt-math-1351">$9.200	\ (e=0,16s\)” class="lt-math-1351">$e=0.16(9,200)=1,472$	A venda de um veículo de $9.200 resulta em ganhos de $1472.
\ (s\), preço de venda” class="lt-math-1351">$4.600	\ (e=0,16s\)” class="lt-math-1351">$e=0.16(4,600)=736$	A venda de um veículo de $4.600 resulta em ganhos de $736.
\ (s\), preço de venda” class="lt-math-1351">$18.400	\ (e=0,16s\)” class="lt-math-1351">$e=0.16(18,400)=2,944$	A venda de um veículo de $18.400 resulta em ganhos de $2944.

Tabela 5.8.1

Observe que os ganhos são um múltiplo das vendas. À medida que as vendas aumentam, os lucros aumentam de forma previsível. Dobramos as vendas do veículo de $4.600 para $9.200, e dobramos os ganhos de $736 para $1.472. Conforme a entrada aumenta, a saída aumenta como um múltiplo da entrada. Uma relação na qual uma quantidade é uma constante multiplicada por outra quantidade é chamada de variação direta. Cada variável nesse tipo de relacionamento varia diretamente com a outra.

A Figura 5.8.1 representa os dados dos ganhos potenciais de Nicole. Dizemos que os ganhos variam diretamente com o preço de venda do carro. A fórmula$y=kx^n$ é usada para variação direta. O valor$k$ é uma constante diferente de zero maior que zero e é chamado de constante de variação. Nesse caso,$k=0.16$$n=1$ e. Vimos funções como essa quando discutimos as funções de potência.

A figura tem fonte inválida: imagem visível até ser salva... src=”/@api /deki/pages/ =BookShelves%252FPrecalculus%252FBook%25253a_precalculus_ (OpenStax) %252F 03% 25253a_polynomial_and_rational_functions%252f 3.9% 25253A_Modeling_Using_Variation/files/CNX_Precalc_Figure_03_09_001.jpg

Uma nota geral: VARIAÇÃO DIRETA

Se$x$ e$y$ estão relacionados por uma equação da forma

$y=kx^n$

então dizemos que a relação é variação direta e$y$ varia diretamente com, ou é proporcional a,$n$ a potência de$x$. Nas relações de variação direta, há uma razão constante diferente de zero$k=\dfrac{y}{x^n}$, chamada de constante de variação, que ajuda a definir a relação entre as variáveis.$k$

Dada a descrição de um problema de variação direta, resolva um desconhecido.

Identifique a entrada$x$, e a saída,$y$.
Determine a constante de variação. Talvez seja necessário dividir$y$ pela potência especificada de$x$ para determinar a constante de variação.
Use a constante de variação para escrever uma equação para a relação.
Substitua valores conhecidos na equação para encontrar o desconhecido.

Exemplo

Resolvendo um problema de variação direta

A quantidade$y$ varia diretamente com o cubo de$x$. Se$y=25$ quando$x=2$, descubra$y$ quando$x$ é$6$.

Solução

A fórmula geral para variação direta com um cubo é$y=kx^3$. A constante pode ser encontrada dividindo-se$y$ pelo cubo de$x$.

$k=\dfrac{y}{x^3}$

$=\dfrac{25}{2^3}$

$=\dfrac{25}{8}$

Agora use a constante para escrever uma equação que represente essa relação.

$y=\dfrac{25}{8}x^3$

Substitua$x=6$ e resolva$y$.

$y=\dfrac{25}{8}{(6)}^3$

$=675$

Análise

O gráfico dessa equação é um cúbico simples, conforme mostrado na Figura 5.8.2.

Gráfico de y=25/8 (x^3) com os pontos rotulados (2, 25) e (6.675). — Figura 5.8.2

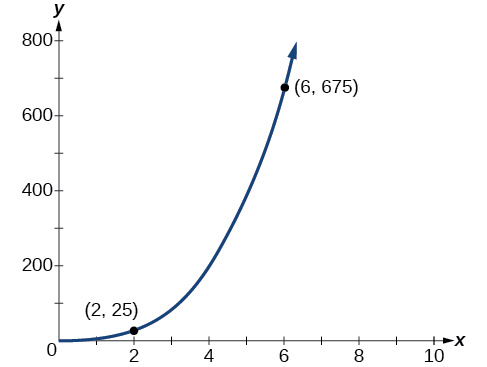
PERGUNTAS E RESPOSTAS

Os gráficos de todas as equações de variação direta se parecem com Example?

Não. As equações de variação direta são funções de potência — elas podem ser lineares, quadráticas, cúbicas, quárticas, radicais, etc. Mas todos os gráficos passam$(0,0)$.

Exercício

A quantidade$y$ varia diretamente com o quadrado de$x$. Se$y=24$ quando$x=3$, descubra$y$ quando$x$ é 4.

Solução

$\frac{128}{3}$

Resolvendo problemas de variação inversa

A temperatura da água em um oceano varia inversamente à profundidade da água. A fórmula nos$T=\frac{14,000}{d}$ dá a temperatura em graus Fahrenheit a uma profundidade em pés abaixo da superfície da Terra. Considere o Oceano Atlântico, que cobre 22% da superfície da Terra. Em um determinado local, a uma profundidade de 500 pés, a temperatura pode ser de 28° F.

Se criarmos a Tabela 5.8.2, observamos que, à medida que a profundidade aumenta, a temperatura da água diminui.

$d$, profundidade	$T=\frac{14,000}{d}$	Interpretação
\ (d\), profundidade” class="lt-math-1351">500 pés	\ (T=\ frac {14.000} {d}\)” class="lt-math-1351">$\frac{14,000}{500}=28$	A uma profundidade de 500 pés, a temperatura da água é de 28° F.
\ (d\), profundidade” class="lt-math-1351">1000 pés	\ (T=\ frac {14.000} {d}\)” class="lt-math-1351">$\frac{14,000}{1000}=14$	A uma profundidade de 1.000 pés, a temperatura da água é de 14° F.
\ (d\), profundidade” class="lt-math-1351">2000 pés	\ (T=\ frac {14.000} {d}\)” class="lt-math-1351">$\frac{14,000}{2000}=7$	A uma profundidade de 2.000 pés, a temperatura da água é de 7° F.

Tabela 5.8.2

Percebemos na relação entre essas variáveis que, à medida que uma quantidade aumenta, a outra diminui. Diz-se que as duas quantidades são inversamente proporcionais e cada termo varia inversamente com o outro. Relações inversamente proporcionais também são chamadas de variações inversas.

Para nosso exemplo, a Figura 5.8.3 mostra a variação inversa. Dizemos que a temperatura da água varia inversamente com a profundidade da água porque, à medida que a profundidade aumenta, a temperatura diminui. A fórmula$y=\frac{k}{x}$ para variação inversa neste caso usa$k=14,000$.

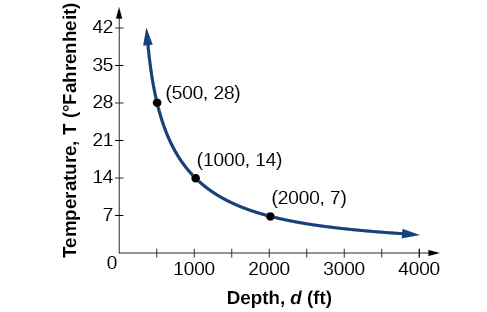
Gráfico de y= (14000) /x onde o eixo horizontal é rotulado como “Profundidade, d (pés)” e o eixo vertical é rotulado como “Temperatura, T (graus Fahrenheit)”. — Figura 5.8.3

Uma nota geral: VARIAÇÃO INVERSA

Se$x$ e$y$ estão relacionados por uma equação da forma

$y=\frac{k}{x^n}$

onde$k$ é uma constante diferente de zero, então dizemos que$y$ varia inversamente com a potência$n$ th de$x$. Em relações inversamente proporcionais, ou variações inversas, há um múltiplo constante$k=x^ny$.

Exemplo

Escrevendo uma fórmula para uma relação inversamente proporcional

Um turista planeja dirigir 100 milhas. Encontre uma fórmula para o tempo que a viagem levará em função da velocidade que o turista dirige.

Solução

Lembre-se de que multiplicar a velocidade pelo tempo dá a distância. Se deixarmos$t$ representar o tempo de viagem em horas e$v$ representarmos a velocidade (velocidade ou taxa) na qual o turista dirige, então a$vt=$ distância. Porque a distância é fixada em 100 milhas,$vt=100$ então$t=\frac{100}{v}$. Como o tempo é uma função da velocidade, podemos escrever$t(v)$.

$t(v)=\frac{100}{v}$

$=100v^{−1}$

Podemos ver que a constante de variação é 100 e, embora possamos escrever a relação usando o expoente negativo, é mais comum vê-la escrita como uma fração. Dizemos que o tempo varia inversamente com a velocidade.

Dada a descrição de um problema de variação indireta, resolva um desconhecido.

Identifique a entrada$x$, e a saída,$y$.
Determine a constante de variação. Talvez seja necessário multiplicar$y$ pela potência especificada de$x$ para determinar a constante de variação.
Use a constante de variação para escrever uma equação para a relação.
Substitua valores conhecidos na equação para encontrar o desconhecido.

Exemplo

Resolvendo um problema de variação inversa

Uma quantidade$y$ varia inversamente com o cubo de$x$. Se$y=25$ quando$x=2$, descubra$y$ quando$x$ é$6$.

Solução

A fórmula geral para variação inversa com um cubo é$y=\frac{k}{x^3}$. A constante pode ser encontrada multiplicando-se$y$ pelo cubo de$x$.

$k=x^3y$

$=2^3⋅25$

$=200$

Agora usamos a constante para escrever uma equação que represente essa relação.

$y=\dfrac{k}{x^3}$,$ k=200$

$y=\dfrac{200}{x^3}$

Substitua$x=6$ e resolva$y$.

$y=\dfrac{200}{6^3}$

$=\dfrac{25}{27}$

Análise

O gráfico dessa equação é uma função racional, conforme mostrado na Figura 5.8.4.

Gráfico de y=25/ (x^3) com os pontos rotulados (2, 25) e (6, 25/27). — Figura 5.8.4

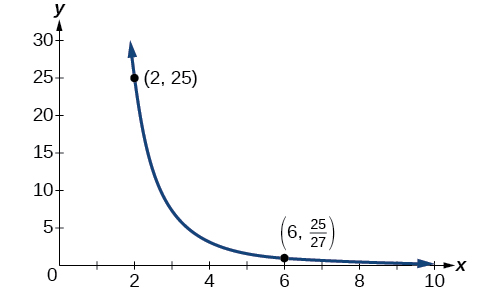
Exercício

Uma quantidade$y$ varia inversamente com o quadrado de$x$. Se$y=8$ quando$x=3$, descubra$y$ quando$x$ é$4$.

Solução

$\frac{9}{2}$

Resolvendo problemas envolvendo variação conjunta

Muitas situações são mais complicadas do que um modelo básico de variação direta ou variação inversa. Uma variável geralmente depende de várias outras variáveis. Quando uma variável depende do produto ou quociente de duas ou mais variáveis, isso é chamado de variação conjunta. Por exemplo, o custo do transporte de ônibus para cada viagem escolar varia com o número de alunos que frequentam e a distância da escola. A variável$c$ custo varia em conjunto com o número de estudantes,$n$, e a distância$d$.

Uma nota geral: VARIAÇÃO CONJUNTA

A variação conjunta ocorre quando uma variável varia direta ou inversamente com várias variáveis.

Por exemplo,$x$ varia diretamente com ambos$y$ e$z$, nós temos$x=kyz$. Se$x$ varia diretamente com$y$ e inversamente com$z$, nós temos$x=\frac{ky}{z}$. Observe que usamos apenas uma constante em uma equação de variação conjunta.

Exemplo

Resolvendo problemas envolvendo variação conjunta

Uma quantidade$x$ varia diretamente com o quadrado de$y$ e inversamente com a raiz cúbica de$z$. Se$x=6$ quando$y=2$ e$z=8$, descubra$x$ quando$y=1$$z=27$ e.

Solução

Comece escrevendo uma equação para mostrar a relação entre as variáveis.

$x=\dfrac{ky^2}{\sqrt[3]{z}}$

Substitua$x=6$$y=2$,, e$z=8$ para encontrar o valor da constante$k$.

$6=\dfrac{k2^2}{\sqrt[3]{8}}$

$6=\dfrac{4k}{2}$

$3=k$

Agora podemos substituir o valor da constante na equação da relação.

$x=\dfrac{3y^2}{\sqrt[3]{z}}$

Para descobrir$x$ quando$y=1$ e$z=27$, substituiremos valores por$y$ e$z$ em nossa equação.

$x=\dfrac{3{(1)}^2}{\sqrt[3]{27}}$

$=1$

Exercício

Uma quantidade$x$ varia diretamente com o quadrado de$y$ e inversamente com$z$. Se$x=40$ quando$y=4$ e$z=2$, descubra$x$ quando$y=10$$z=25$ e.

Solução

$x=20$

Mídia

Acesse esses recursos on-line para obter instruções e práticas adicionais com variação direta e inversa.

Visite este site para obter mais perguntas práticas do Learningpod.

Equações-chave

Variação direta	$y=kx^n$,$k$ é uma constante diferente de zero.
Variação inversa	$y=\dfrac{k}{x^n}$,$k$ é uma constante diferente de zero.

Conceitos-chave

Uma relação em que uma quantidade é uma constante multiplicada por outra quantidade é chamada de variação direta. Veja o exemplo.
Duas variáveis que são diretamente proporcionais uma à outra terão uma proporção constante.
Uma relação em que uma quantidade é uma constante dividida por outra quantidade é chamada de variação inversa. Veja o exemplo.
Duas variáveis que são inversamente proporcionais uma à outra terão um múltiplo constante. Veja o exemplo.
Em muitos problemas, uma variável varia direta ou inversamente com várias variáveis. Chamamos esse tipo de variação conjunta de relacionamento. Veja o exemplo.

\(s\), preço de venda	\(e=0.16s\)	Interpretação
\ (s\), preço de venda” class="lt-math-1351">$9.200	\ (e=0,16s\)” class="lt-math-1351">\(e=0.16(9,200)=1,472\)	A venda de um veículo de $9.200 resulta em ganhos de $1472.
\ (s\), preço de venda” class="lt-math-1351">$4.600	\ (e=0,16s\)” class="lt-math-1351">\(e=0.16(4,600)=736\)	A venda de um veículo de $4.600 resulta em ganhos de $736.
\ (s\), preço de venda” class="lt-math-1351">$18.400	\ (e=0,16s\)” class="lt-math-1351">\(e=0.16(18,400)=2,944\)	A venda de um veículo de $18.400 resulta em ganhos de $2944.

Variação direta	\(y=kx^n\),\(k\) é uma constante diferente de zero.
Variação inversa	\(y=\dfrac{k}{x^n}\),\(k\) é uma constante diferente de zero.