2.E: Funções lineares (exercícios)

2.1 Funções lineares

Verbal

1) Terry está esquiando em uma colina íngreme. A elevação de Terry$E(t)$, em pés após$t$ segundos, é dada por$E(t)=3000−70t$. Escreva uma frase completa descrevendo a elevação inicial de Terry e como ela está mudando com o tempo.

Resposta

Terry começa com uma elevação de$3000$ pés e desce$70$ pés por segundo.

2) Maria está escalando uma montanha. A elevação de Maria$E(t)$, em pés após$t$ minutos, é dada por$E(t)=1200+40t$. Escreva uma frase completa descrevendo a elevação inicial de Maria e como ela está mudando com o tempo.

3) Jessica está voltando para casa da casa de um amigo. Depois de$2$ alguns minutos, ela está$1.4$ a quilômetros de casa. Doze minutos depois de sair, ela está$0.9$ a milhas de casa. Qual é a tarifa dela em milhas por hora?

Resposta

$3$milhas por hora

4) Sonya está atualmente$10$ a milhas de casa e está caminhando mais longe a$2$ milhas por hora. Escreva uma equação para a distância dela de casa a$t$ partir de agora.

5) Um barco está a$100$ quilômetros de distância da marina, navegando diretamente em direção a ela$10$ a milhas por hora. Escreva uma equação para a distância do barco da marina após o$t$ expediente.

Resposta

$d(t) =100−10t$

6) Timmy vai à feira com$\$40$. Cada viagem custa$\$2$. Quanto dinheiro ele terá sobrando depois de andar de$n$ bicicleta?

Algébrico

Para os exercícios 7-14, determine se a equação da curva pode ser escrita como uma função linear.

7)$y= \dfrac{1}{4}x+6$

Resposta

sim

8)$y=3x−5$

9)$y=3 x^2 −2$

Resposta

Não

10)$3x+5y=15$

11)$3 x^2 +5y=15$

Resposta

Não

12)$3x+5 y^ 2 =15$

13)$−2 x^2 +3y^2 =6$

Resposta

Não

14)$−\dfrac{x−3}{5} =2y$

Para os exercícios 15-24, determine se cada função está aumentando ou diminuindo.

15)$f(x)=4x+3$

Resposta

Aumentando

16)$g(x)=5x+6$

17)$a(x)=5−2x$

Resposta

Decrescente

18)$b(x)=8−3x$

19)$h(x)=−2x+4$

Resposta

Decrescente

20)$k(x)=−4x+1$

21)$j(x)=\dfrac{1}{2}x−3$

Resposta

Aumentando

22)$p(x)=\dfrac{1}{4}x−5$

23)$n(x)=−\dfrac{1}{3}x−2$

Resposta

Decrescente

24)$m(x)=−\dfrac{3}{8}x+3$

Para os exercícios 25-29, encontre a inclinação da linha que passa pelos dois pontos dados.

25)$(2, 4)$ e$(4, 10)$

Resposta

$3$

26)$(1, 5)$ e$(4, 11)$

27)$(−1,4)$ e$(5,2)$

Resposta

$–\dfrac{1}{3}$

28)$(8,−2)$ e$(4,6)$

29) (6, 11) e (−4, 3)

Resposta

$\dfrac{4}{5}$

Para os exercícios 30-37, dado cada conjunto de informações, encontre uma equação linear que satisfaça as condições, se possível.

30)$f(−5)=−4$ e$f(5)=2$

31)$f(−1)=4$ e$f(5)=1$

Resposta

$f(x)=−\dfrac{1}{2}x+\dfrac{7}{2}$

32)$(2,4)$ e$(4,10)$

33) Passa por$(1,5)$ e$(4,11)$

Resposta

$y=2x+3$

34) Passa por$(−1, 4)$ e$(5, 2)$

35) Passa por$(−2, 8)$ e$(4, 6)$

Resposta

$y=−\dfrac{1}{3}x+\dfrac{22}{3}$

36)$x$ interceptar em (−2, 0) e$y$ interceptar em (0, −3)

37)$x$ interceptar em (−5, 0) e$y$ interceptar em (0, 4)

Resposta

$y=\dfrac{4}{5}x+4$

Gráfica

Para os exercícios 38-,40, determine a inclinação das linhas representadas graficamente.

38)

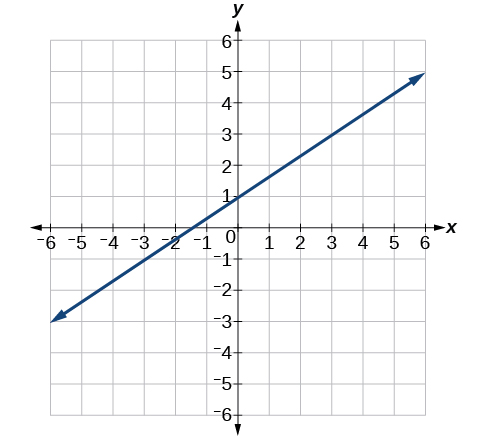
39)

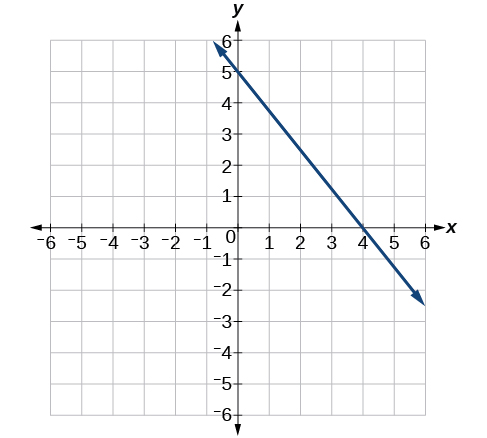
Resposta

$−\dfrac{5}{4}$

40)

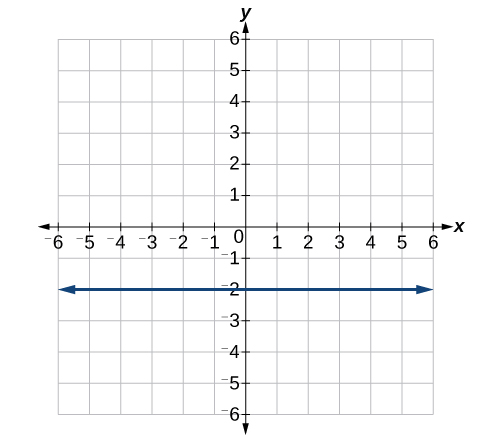
Para os exercícios 41-46, escreva uma equação para as linhas representadas graficamente.

41)

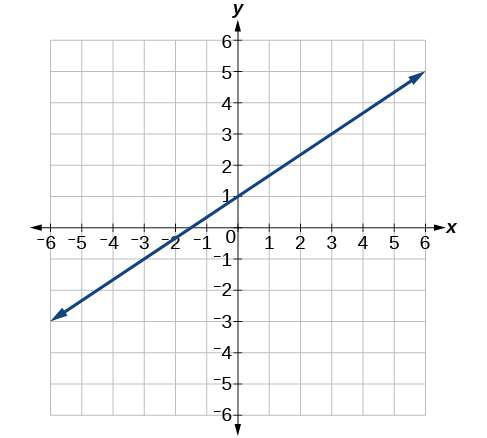
Resposta

$y= \dfrac{2}{3} x+1$

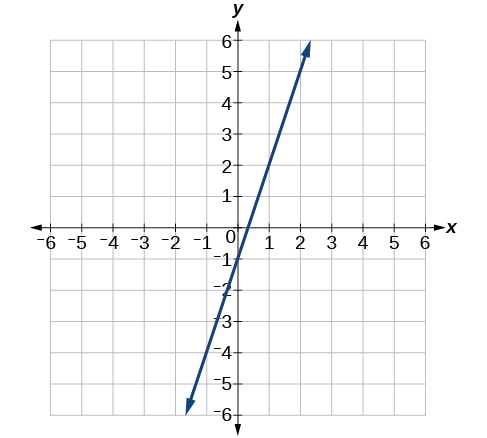
42)

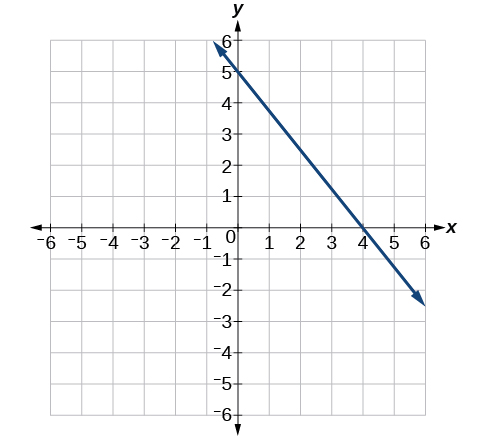
43)

Resposta

$y=−2x+3$

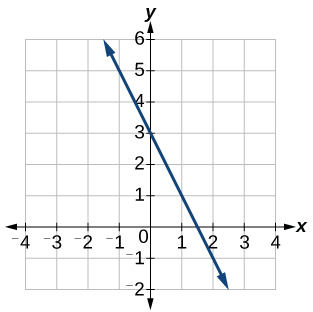
44)

45)

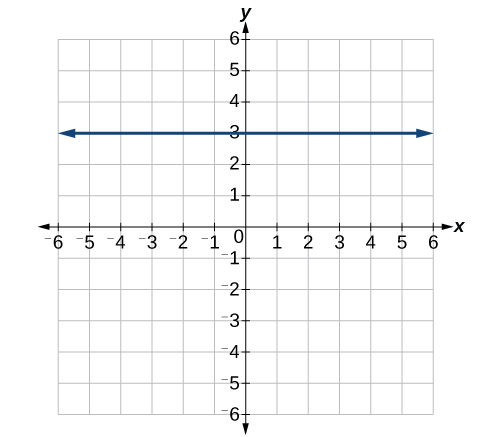
Resposta

$y=3$

46)

Numérico

Para os exercícios 47-51, qual das tabelas poderia representar uma função linear? Para cada uma que possa ser linear, encontre uma equação linear que modela os dados.

47)

$x$	0	5	10	15
$g(x)$	5	—10	—25	—40

Resposta

Linear,$g(x)=−3x+5$

48)

$x$	0	5	10	15
$h(x)$	5	30	105	230

$x$	0	5	10	15
$f(x)$	—5	20	45	70

Resposta

Linear,$f(x)=5x−5$

49)

$x$	5	10	20	25
$k(x)$	28	13	58	73

$x$	0	2	4	6
$g(x)$	6	—19	—44	—69

Resposta

Linear,$g(x)=−\dfrac{25}{2}x+6$

50)

$x$	2	4	6	8
$f(x)$	—4	16	36	56

$x$	2	4	6	8
$f(x)$	—4	16	36	56

Resposta

Linear,$f(x)=10x−24$

51)

$x$	0	2	6	8
$k(x)$	6	31	106	231

Tecnologia

52) Se$f$ for uma função linear,$f(0.1)=11.5$, e$f(0.4)=–5.9$, encontre uma equação para a função.

Resposta

$f(x)=−58x+17.3$

53) Representar graficamente a função$f$ em um domínio de$[ –10, 10 ]: f(x)=0.02x−0.01$. Insira a função em um utilitário gráfico. Para a janela de visualização, defina o valor mínimo de$x$ como −10 e o valor máximo$x$ de como 10.

54) Representar graficamente a função$f$ em um domínio de$[ –10, 10 ]:fx)=2,500x+4,000$

Resposta

55) A tabela abaixo mostra a entrada e a saída para uma função linear$k$.$w$$k$

1. Preencha os valores que faltam na tabela.
2. Escreva a função linear$k$, arredondando para$3$ casas decimais.

$w$	—10	5.5	67,5	b
$k$	30	—26	uma	—44

56) A tabela abaixo mostra a entrada e a saída para uma função linear$q$.$p$$q$

1. Preencha os valores que faltam na tabela.
2. Escreva a função linear$k$.

$p$	0,5	0,8	12	b
$q$	400	700	uma	1.000.000

Resposta

1. $a=11$3.900;$b=1001.1$
2. $q(p)=1000p−100$

57) Faça um gráfico da função linear$f$ em um domínio de$[ −10,10 ]$ para a função cuja inclinação é$\dfrac{1}{8}$ e o intercepto y é$\dfrac{31}{16}$. Identifique os pontos para os valores de entrada de$−10$$10$ e.

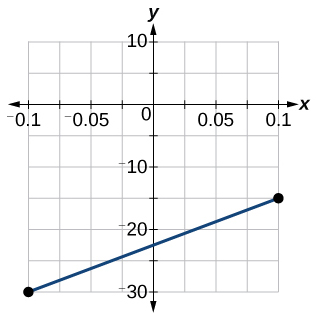
58) Faça um gráfico da função linear$f$ em um domínio de$[ −0.1,0.1 ]$ para a função cuja inclinação é$75$ e$y$ -intercepto é$-22.5$. Identifique os pontos para os valores de entrada de$-0.1$$0.1$ e.

Resposta

59) Faça um gráfico da função linear$f$$f(x)=ax+b$ em que está no mesmo conjunto de eixos em um domínio de$[ −4,4 ]$ para os seguintes valores de$a$$b$ e.

1. $a=2;$$b=3$
2. $a=2;$$b=4$
3. $a=2;$$b=–4$
4. $a=2;$$b=–5$

Extensões

60) Encontre o valor de$x$ se uma função linear passa pelos seguintes pontos e tem a seguinte inclinação:$(x,2),(−4,6),$$m=3$

Resposta

$x=−\dfrac{16}{3}$

61) Encontre o valor de$y$ se uma função linear passa pelos seguintes pontos e tem a seguinte inclinação:$(10,y),(25,100),$$m=−5$

62) Encontre a equação da reta que passa pelos seguintes pontos:$(a, b)$ e$( a, b+1 )$

Resposta

$x=a$

63) Encontre a equação da reta que passa pelos seguintes pontos:$(2a, b)$ e (a, b+1)

64) Encontre a equação da reta que passa pelos seguintes pontos:$(a, 0)$ e$(c, d)$

Resposta

$y=\dfrac{d}{c−a}x−\dfrac{ad}{c−a}$

Aplicativos do mundo real

65) Ao meio-dia, um barista percebe que ela tem$\$20$ em sua jarra de gorjetas. Se ela fizer uma média$\$0.50$ de cada cliente, quanto ela terá em seu pote de gorjetas se atender$n$ mais clientes durante o turno?

66) Uma associação à academia com duas sessões de treinamento pessoal custa$\$125$, enquanto a associação à academia com cinco sessões de treinamento pessoal custa$\$260$. Qual é o custo por sessão?

Resposta

$\$45$por sessão de treinamento.

67) Uma empresa de roupas descobre que existe uma relação linear entre o número de camisas$n$, ela pode vender e o preço$p$, pode cobrar por camisa. Em particular, dados históricos mostram que$1,000$ camisas podem ser vendidas a um preço de$\$30$, enquanto$3,000$ camisas podem ser vendidas a um preço de$\$22$. Encontre uma equação linear no formato$p(n)=mn+b$ que forneça o preço que$p$ eles podem cobrar pelas$n$ camisas.

68) Uma companhia telefônica cobra pelo serviço de acordo com a fórmula:$C(n)=24+0$ .1n, onde$n$ está o número de minutos falados, e$C(n)$ é a cobrança mensal, em dólares. Encontre e interprete a taxa de variação e o valor inicial.

Resposta

A taxa de mudança é$0.1$. Para cada minuto adicional falado, a cobrança mensal aumenta em$\$0.1$ ou em$10$ centavos. O valor inicial é$24$. Quando não há minutos falados, inicialmente a cobrança é$\$24$.

69) Um agricultor descobre que existe uma relação linear entre o número de talos de feijão$n$, ela planta e o rendimento$y$, que cada planta produz. Quando ela planta$30$ talos, cada planta produz$30$ onças de feijão. Quando ela planta$34$ talos, cada planta produz$28$ onças de feijão. Encontre relações lineares na forma$y=mn+b$ que dê o rendimento quando os$n$ caules são plantados.

70) A população de uma cidade no ano 1960 era$287,500$. Em 1989, a população era$275,900$. Calcule a taxa de crescimento da população e faça uma declaração sobre a taxa de mudança populacional de pessoas por ano.

Resposta

A inclinação é$-400$. Isso significa que para cada ano entre 1960 e 1989, a população caiu$400$ por ano na cidade.

71) A população de uma cidade tem crescido linearmente. Em 2003, a população era$45,000$, e a população vem crescendo em$1,700$ pessoas a cada ano. Escreva uma equação,$P(t)$, para a população$t$ anos após 2003.

72) Suponha que a renda média anual (em dólares) dos anos 1990 a 1999 seja dada pela função linear:$I(x)=1054x+23$,$286,$ onde$x$ é o número de anos após 1990. Qual das seguintes opções interpreta a inclinação no contexto do problema?

1. Em 1990, a renda média anual era$\$23,286$.
2. No período de dez anos de 1990-1999, a renda média anual aumentou em um total de$\$1,054$.
3. A cada ano, na década de 1990, a renda média anual aumentou em $1.054.
4. A renda média anual subiu para um nível de $23.286 no final de 1999.

Resposta

c

73) Quando a temperatura é de$0$ graus Celsius, a temperatura em Fahrenheit é$32$. Quando a temperatura Celsius é$100$, a temperatura correspondente em Fahrenheit é$212$. Expresse a temperatura em Fahrenheit como uma função linear da temperatura Celsius,$F(C)$.$C$

1. Encontre a taxa de variação da temperatura em Fahrenheit para cada temperatura de mudança unitária de Celsius.
2. Encontre e interprete$F(28)$.
3. Encontre e interprete$F(–40)$.

2.2 Gráficos de funções lineares

Verbal

1) Se os gráficos de duas funções lineares forem paralelos, descreva a relação entre as inclinações e os$y$ interceptos.

Resposta

As inclinações são iguais;$y$ -interceptações não são iguais.

2) Se os gráficos de duas funções lineares forem perpendiculares, descreva a relação entre as inclinações e os$y$ interceptos.

3) Se uma linha horizontal tem a equação$f(x)=a$ e uma linha vertical tem a equação$x=a$, qual é o ponto de interseção? Explique por que o que você encontrou é o ponto de interseção.

Resposta

O ponto de interseção é$(a,a)$. Isso ocorre porque, para a linha horizontal, todas as$y$ coordenadas são a e, para a linha vertical, todas as$x$ coordenadas são a. O ponto de interseção terá essas duas características.

4) Explique como encontrar uma linha paralela a uma função linear que passa por um determinado ponto.

5) Explique como encontrar uma linha perpendicular a uma função linear que passa por um determinado ponto.

Resposta

Primeiro, encontre a inclinação da função linear. Em seguida, pegue o recíproco negativo da inclinação; essa é a inclinação da linha perpendicular. Substitua a inclinação da linha perpendicular e a coordenada do ponto dado na equação$y=mx+b$ e resolva por$b$. Em seguida, escreva a equação da linha no formulário$y=mx+b$ substituindo em$m$$b$ e.

Algébrico

Para os exercícios 6-11, determine se as retas dadas pelas equações abaixo são paralelas, perpendiculares ou nem paralelas nem perpendiculares:

6)$4x−7y=10 \\ 7x+4y=1$

7)$3y+x=12 \\ −y=8x+1$

Resposta

nem paralelo nem perpendicular

8)$3y+4x=12 \\ −6y=8x+1$

9)$6x−9y=10 \\ 3x+2y=1$

Resposta

perpendiculares

10)$y=\dfrac{2}{3}x+1 \\ 3x+2y=1$

11)$y=\dfrac{3}{4}x+1 \\ −3x+4y=1$

Resposta

paralelo

Para os exercícios 12-17, encontre os$y$ interceptos$x$ - e -de cada equação

12)$f(x)=−x+2$

13)$g(x)=2x+4$

Responda

$(–2, 0); (0, 4)$

14)$h(x)=3x−5$

15)$k(x)=−5x+1$

Responda

$\left(\dfrac{1}{5}, 0\right); (0, 1)$

16)$−2x+5y=20$

17)$7x+2y=56$

Responda

$(8, 0); (0, 28)$

Para os exercícios 18-23, use as descrições de cada par de linhas abaixo para encontrar as inclinações da Linha 1 e da Linha 2. Cada par de linhas é paralelo, perpendicular ou nenhum dos dois?

18)

Linha 1: Passa$(0,6)$ e$(3,−24)$
Linha 2: Passa por$(−1,19)$ e$(8,−71)$

19)

Linha 1: Passa$(−8,−55)$ e$(10, 89)$
Linha 2: Passa por$(9,−44)$ e$(4,−14)$

Responda

Linha 1:$m=8$ Linha 2:$m=–6$ Nenhuma

20)

Linha 1: Passa por$(2,3)$ e (4, −1)
Linha 2: Passa por$(6,3)$ e$(8,5)$

21)

Linha 1: Passa$(1,7)$ e$(5,5)$
Linha 2: Passa por$(−1,−3)$ e$(1,1)$

Responda

Linha 1:$m=–12$ Linha 2:$m=2$ Perpendicular

22)

Linha 1: Passa$(0,5)$ e$(3,3)$
Linha 2: Passa por$(1,−5)$ e$(3,−2)$

23)

Linha 1: Passa$(2,5)$ e$(5,−1)$
Linha 2: Passa por$(−3,7)$ e$(3,−5)$

Responda

Linha 1:$m=–2$ Linha 2:$m=–2$ Paralela

24) Escreva uma equação para uma linha paralela$f(x)=−5x−3$ e passando pelo ponto$(2, –12)$.

25) Escreva uma equação para uma linha paralela$g(x)=3x−1$ e passando pelo ponto$(4,9)$.

Responda

$g(x)=3x−3$

26) Escreva uma equação para uma reta perpendicular$h(t)=−2t+4$ e passando pelo ponto$(-4, –1)$.

27) Escreva uma equação para uma reta perpendicular$p(t)=3t+4$ e passando pelo ponto$(3,1)$.

Responda

$p(t)=−\dfrac{1}{3}t+2$

28) Encontre o ponto em que a linha$f(x)=−2x−1$ cruza a linha$g(x)=−x$.

29) Encontre o ponto em que a linha$f(x)=2x+5$ cruza a linha$g(x)=−3x−5$.

Responda

$(−2,1)$

30) Use álgebra para encontrar o ponto em que a linha$f(x)= −\dfrac{4}{5}x +\dfrac{274}{25}$ cruza a linha$h(x)=\dfrac{9}{4}x + \dfrac{73}{10}$.

31) Use álgebra para encontrar o ponto em que a linha$f(x)=\dfrac{7}{4}x + \dfrac{457}{60}$ cruza a linha$g(x)=\dfrac{4}{3}x + \dfrac{31}{5}$.

Responda

$\left(−\dfrac{17}{5},\dfrac{5}{3}\right)$

Gráfica

Para os exercícios 32-37, combine a equação linear dada com seu gráfico na Figura abaixo.

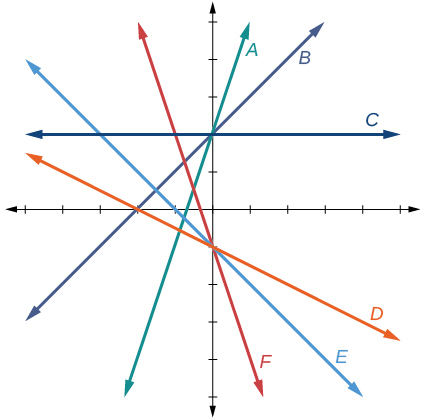
32)$f(x)=−x−1$

33)$f(x)=−2x−1$

Responda

F

34)$f(x)=−\dfrac{1}{2}x−1$

(35)$f(x)=2$

Responda

C

36)$f(x)=2+x$

37)$f(x)=3x+2$

Responda

UMA

Para os exercícios 38-43, desenhe uma linha com as características fornecidas.

38) Um$x$ -intercepto de$(–4, 0)$ e$y$ -intercepto de$(0, –2)$

39) Um$x$ -intercepto de$(–2, 0)$ e$y$ -intercepto de$(0, 4)$

Responda

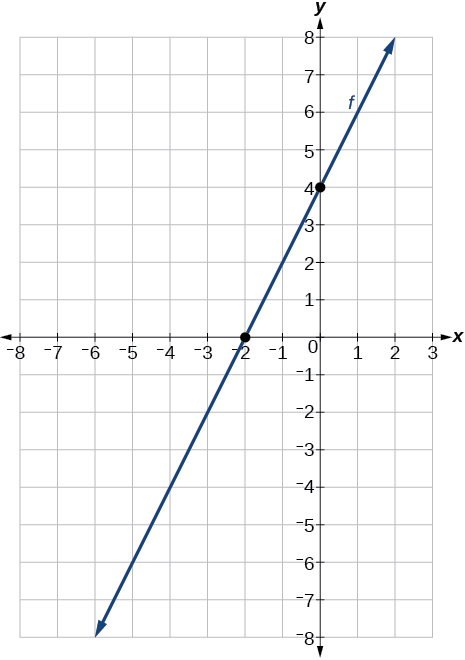
40) Um$y$ -intercepto de$(0, 7)$ e inclinação$−\dfrac{3}{2}$

41) Uma$y$ interceptação de$(0, 3)$ e inclinação$\dfrac{2}{5}$

Responda

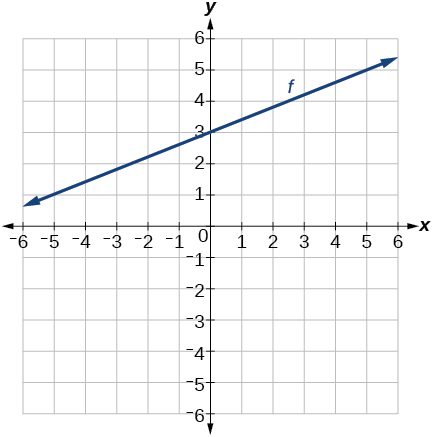
42) Passando pelos pontos$(–6, –2)$ e$(6, –6)$

43) Passando pelos pontos$(–3, –4)$ e$(3, 0)$

Responda

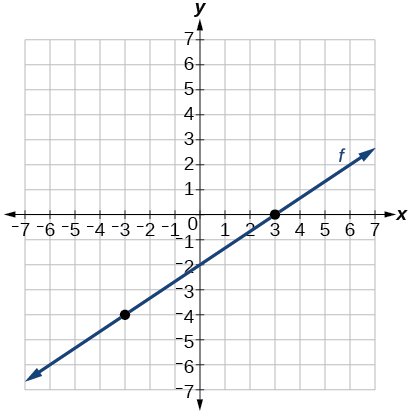
Para os exercícios 44-58, esboce o gráfico de cada equação.

44)$f(x)=−2x−1$

45)$g(x)=−3x+2$

Responda

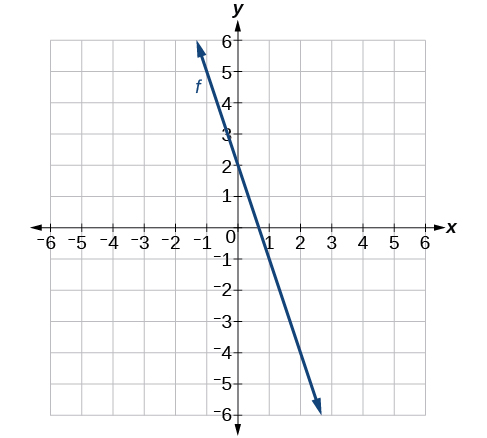
(46)$h(x)=\dfrac{1}{3}x+2$

47)$k(x)=\dfrac{2}{3}x−3$

Responda

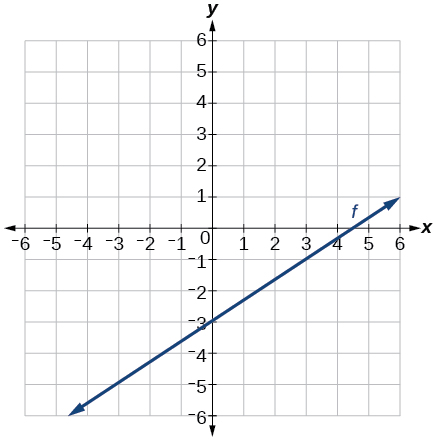
48)$f(t)=3+2t$

49)$p(t)=−2 + 3t$

Responda

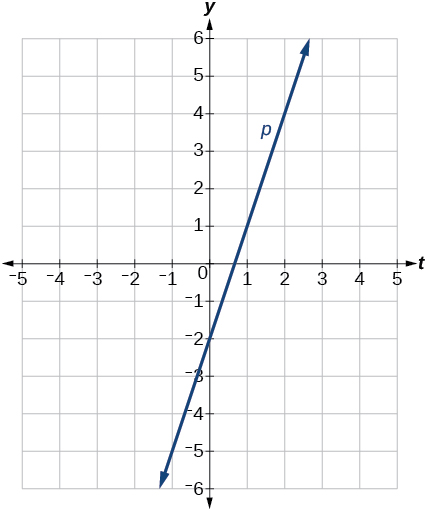
50)$x=3$

51)$x=−2$

Responda

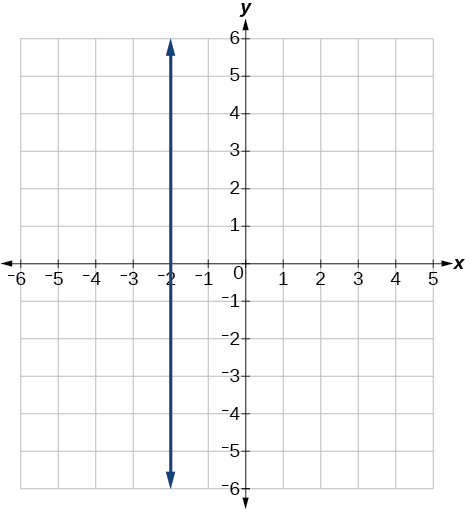
52)$r(x)=4$

53)$q(x)=3$

Responda

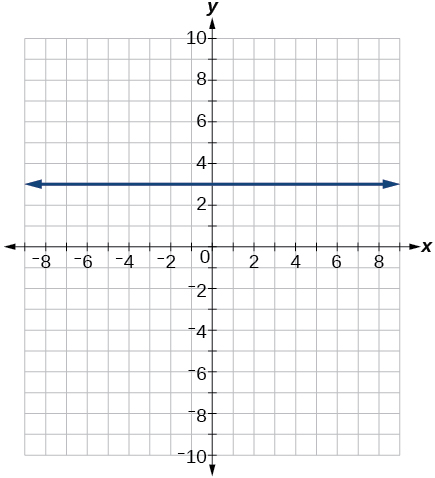
54)$4x=−9y+36$

55)$\dfrac{x}{3}−\dfrac{y}{4}=1$

Responda

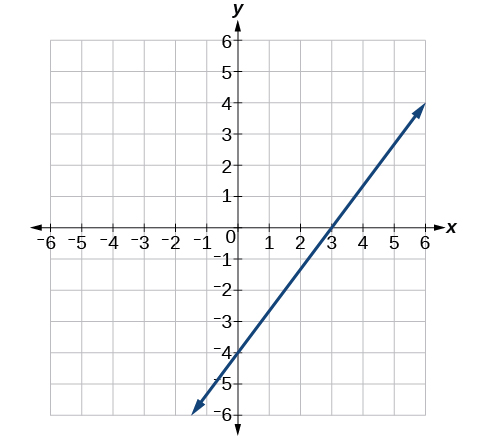
(56)$3x−5y=15$

57)$3x=15$

Responda

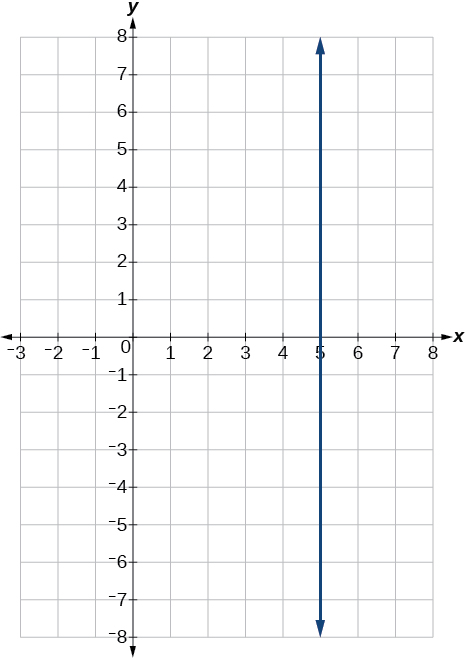
(58)$3y=12$

59) Se$g(x)$ é a transformação de$f(x)=x$ após uma compressão vertical em$\dfrac{3}{4}$, um deslocamento para a direita e um deslocamento para baixo em$2$$4$

1. Escreva uma equação para$g(x)$.
2. Qual é a inclinação dessa linha?
3. Encontre o$y$ intercepto -desta linha.

Responda

1. $g(x)=0.75x−5.5$
2. $0.75$
3. $0,-5.5)$

60) Se$g(x)$ é a transformação de$f(x)=x$ após uma compressão vertical em$\dfrac{1}{3}$, um deslocamento para a esquerda e um deslocamento para cima em$1$$3$

1. Escreva uma equação para$g(x)$.
2. Qual é a inclinação dessa linha?
3. Encontre o$y$ intercepto -desta linha.

Para os exercícios 61-64, escreva a equação da linha mostrada no gráfico.

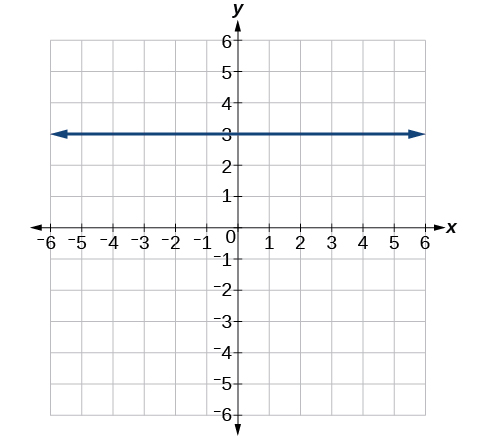
61)

Responda

$y=3$

62)

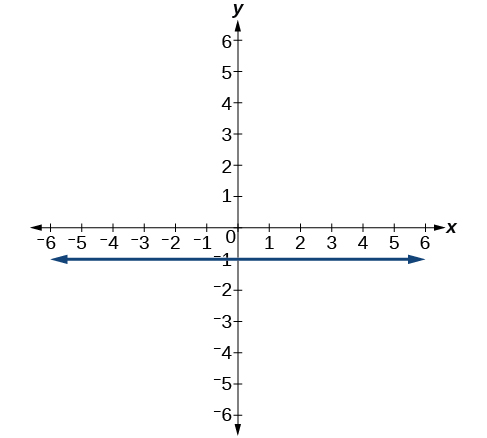
63)

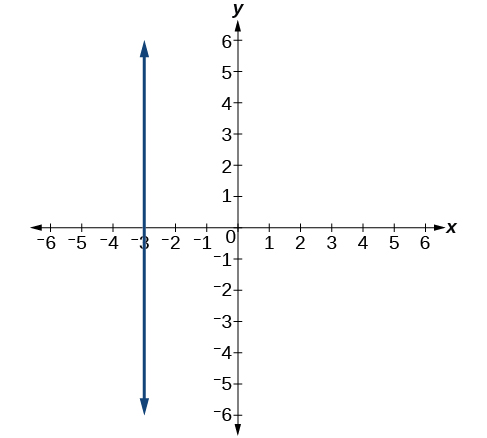
Responda

$x=−3$

64)

Para os exercícios 65-69, encontre o ponto de interseção de cada par de linhas, se ele existir. Se não existir, indique que não há nenhum ponto de interseção.

65)$y=\dfrac{3}{4}x+1 \\ −3x+4y=12$

Responda

nenhum ponto de interseção

66)$2x−3y=12 \\ 5y+x=30$

67)$2x=y−3 \\ y+4x=15$

Responda

$(2, 7)$

68)$x−2y+2=3 \\ x−y=3$

69)$5x+3y=−65 \\ x−y=−5$

Responda

$(–10, –5)$

Extensões

70) Encontre a equação da reta paralela à linha que$g(x)=−0.01x + 2.01$ passa pelo ponto$(1, 2)$.

71) Encontre a equação da reta perpendicular à reta que$g(x)=−0.01x+2.01$ passa pelo ponto$(1, 2)$.

Responda

$y=100x−98$

Para os exercícios 72-73, use as funções$f(x)=−0.1x+200$$g(x)=20x+0.1$ e.

72) Encontre o ponto de interseção das linhas$f$$g$ e.

73) Onde é$f(x)$ maior que$g(x)?$ Onde é$g(x)$ maior que$f(x)?$

Responda

$x<\dfrac{1999}{201}x>\dfrac{1999}{201}$

Aplicativos do mundo real

74) Uma locadora de veículos oferece dois planos para alugar um carro.

Plano A:$\$30$ por dia e$\$0.18$ por milha
Plano B:$\$50$ por dia com quilometragem gratuita ilimitada

Quantas milhas você precisaria dirigir para o plano B para economizar dinheiro?

75) Uma empresa de telefonia celular oferece dois planos por minutos.

Plano A:$\$20$ por mês e$\$1$ para cada cem textos.
Plano B:$\$50$ por mês com textos ilimitados gratuitos.

Quantos textos você precisaria enviar por mês para o plano B para economizar dinheiro?

Responda

Menos que$3000$ textos

76) Uma empresa de telefonia celular oferece dois planos por minutos.

Plano A:$\$15$ por mês e$\$2$ para todos os$300$ textos.
Plano B:$\$25$ por mês e$\$0.50$ para todos os$100$ textos.

Quantos textos você precisaria enviar por mês para o plano B para economizar dinheiro?

2.3 Modelagem com funções lineares

Verbal

1) Explique como encontrar a variável de entrada em um problema de palavras que usa uma função linear.

Responda

Determine a variável independente. Essa é a variável da qual a saída depende.

2) Explique como encontrar a variável de saída em um problema de palavras que usa uma função linear.

3) Explique como interpretar o valor inicial em um problema de palavras que usa uma função linear.

Responda

Para determinar o valor inicial, encontre a saída quando a entrada for igual a zero.

4) Explique como determinar a inclinação em um problema de palavras que usa uma função linear.

Algébrico

5) Encontre a área de um paralelogramo delimitada pelo$y$ eixo, a linha$x=3$, a linha$f(x)=1+2x$ e a linha paralela à$f(x)$ passagem (2, 7).

Responda

$6$unidades quadradas

6) Encontre a área de um triângulo delimitada pelo$x$ eixo -, a linha$f(x)=12–\dfrac{1}{3}x$ e a linha perpendicular a$f(x)$ que passa pela origem.

7) Encontre a área de um triângulo delimitada pelo$y$ eixo -, a linha$f(x)=9–\dfrac{6}{7}x$ e a linha perpendicular a$f(x)$ que passa pela origem.

Responda

$20.012$unidades quadradas

8) Encontre a área de um paralelogramo delimitada pelo$x$ eixo -, a linha$g(x)=2$, a linha$f(x)=3x$ e a linha paralela à$f(x)$ passagem (6,1).

Para os exercícios 9-10, considere este cenário: a população de uma cidade vem diminuindo a uma taxa constante. Em 2010, a população era$5,900$. Em 2012, a população havia caído$4,700$. Suponha que essa tendência continue.

9) Preveja a população em 2016.

Responda

$2,300$

10) Identifique o ano em que a população chegará$0$.

Para os exercícios 11-12, considere este cenário: a população de uma cidade aumentou a uma taxa constante. Em 2010, a população era$46,020$. Em 2012, a população aumentou para$52,070$. Suponha que essa tendência continue.

11) Preveja a população em 2016.

Responda

$64,170$

12) Identifique o ano em que a população chegará$75,000$.

Para os exercícios 13-18, considere este cenário: Uma cidade tem uma população inicial de$75,000$. Ela cresce a uma taxa constante de$2,500$ por ano durante$5$ anos.

13) Encontre a função linear que modela a população$P$ da cidade em função do ano,$t$, onde$t$ está o número de anos desde que o modelo começou.

Responda

$P(t)=75,000+2500t$

14) Encontre um domínio e um intervalo razoáveis para a função$P$.

15) Se a função$P$ for representada graficamente, encontre e interprete os$y$ interceptos$x$ - e -.

Responda

$(-30, 0)$Trinta anos antes do início desse modelo, a cidade não tinha. $(0, 75,000)$Inicialmente, a cidade tinha uma população de$75,000$.

16) Se a função$P$ estiver representada graficamente, encontre e interprete a inclinação da função.

17) Quando a saída será alcançada$100,000$?

Responda

Dez anos após o início do modelo.

18) Qual é a produção nos$12$ anos anuais a partir do início do modelo?

Para os exercícios 19-24, considere este cenário: o peso de um recém-nascido é de$7.5$ libras. O bebê engordou meio quilo por mês no primeiro ano.

19) Encontre a função linear que modela o peso$W$ do bebê em função da idade do bebê, em meses$t$.

Responda

$W(t)=7.5t+0.5$

20) Encontre um domínio e um intervalo razoáveis para a função$W$.

21) Se a função$W$ for representada graficamente, encontre e interprete os$y$ interceptos$x$ - e -.

Responda

$(−15,0)$: O$x$ intercepto -não é um conjunto de dados plausível para este modelo porque significa que o bebê pesava$0$ libras$15$ meses antes do nascimento. $(0, 7.5)$: O bebê pesava$7.5$ quilos ao nascer.

22) Se a função$W$ estiver representada graficamente, encontre e interprete a inclinação da função.

23) Quando o bebê pesou$10.4$ quilos?

Responda

Aos$5.8$ meses de idade.

24) Qual é a saída quando a entrada é$6.2$? Interprete sua resposta.

Para os exercícios 25-30, considere este cenário: o número de pessoas afetadas pelo resfriado comum nos meses de inverno diminuiu constantemente a$205$ cada ano, de 2005 a 2010. Em 2005,$12,025$ as pessoas foram afligidas.

25) Encontre a função linear que modela o número de pessoas infligidas pelo$C$ resfriado comum em função do ano,$t$.

Responda

$C(t)=12,025−205t$

26) Encontre um domínio e um intervalo razoáveis para a função$C$.

27) Se a função$C$ for representada graficamente, encontre e interprete os$y$ interceptos$x$ - e -.

Responda

$(58.7, 0)$: Em aproximadamente$59$ anos, o número de pessoas infligidas pelo resfriado comum seria$0$. $(0,12,025)$: Inicialmente, havia$12,025$ pessoas afetadas pelo resfriado comum.

28) Se a função$C$ estiver representada graficamente, encontre e interprete a inclinação da função.

29) Quando a saída chegará$0$?

Responda

$2064$

30) Em que ano será o número de pessoas$9,700$?

Gráfica

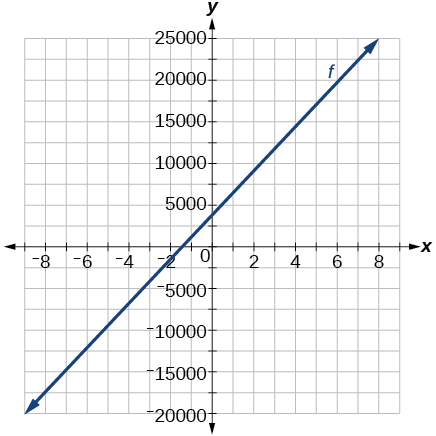
Para os exercícios 31-34, use o gráfico na Figura abaixo, que mostra o lucro$y$, em milhares de dólares, de uma empresa em um determinado ano$t$, onde$t$ representa o número de anos desde 1980.

31) Encontre a função linear$y$, onde$y$ depende$t$, do número de anos desde 1980.

Responda

$y=−2t+180$

32) Encontre e interprete o$y$ intercepto.

33) Encontre e interprete o$x$ intercepto.

Responda

Em 2070, o lucro da empresa será zero.

34) Encontre e interprete a inclinação.

Para os exercícios 35-38, use o gráfico na Figura abaixo, que mostra o lucro$y$, em milhares de dólares, de uma empresa em um determinado ano$t$, onde$t$ representa o número de anos desde 1980.

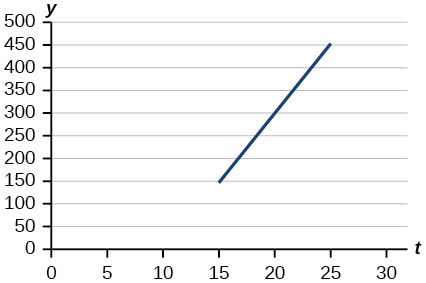
35) Encontre a função linear$y$, onde$y$ depende$t$, do número de anos desde 1980.

Responda

$y=30t−300$

36) Encontre e interprete o$y$ intercepto.

37) Encontre e interprete o$x$ intercepto.

Responda

$(10, 0)$Em 1990, o lucro gerou lucro zero.

38) Encontre e interprete a inclinação.

Numérico

Para os exercícios 39-41, use os valores médios das casas no Mississippi e no Havaí (ajustados pela inflação) mostrados na Tabela abaixo. Suponha que os valores da casa estejam mudando linearmente.

Ano	Mississippi	Havaí
1950	$25.200	$74.400
2000	$71.400	$272.700

39) Em qual estado os valores das casas aumentaram a uma taxa maior?

Responda

Havaí

40) Se essas tendências continuassem, qual seria o valor médio da casa no Mississippi em 2010?

41) Se assumirmos que a tendência linear existiu antes de 1950 e continua depois de 2000, os valores médios das casas dos dois estados serão (ou foram) iguais em que ano? (A resposta pode ser absurda.)

Responda

Durante o ano de 1933

Para os exercícios 42-44, use os valores médios das casas em Indiana e Alabama (ajustados pela inflação) mostrados na Tabela abaixo. Suponha que os valores da casa estejam mudando linearmente.

Ano	Indiana	Alabama
1950	$37.700	$27.100
2000	$94.300	$85.100

42) Em qual estado os valores das casas aumentaram a uma taxa maior?

43) Se essas tendências continuassem, qual seria o valor médio da casa em Indiana em 2010?

Responda

$\$105,620$

44) Se assumirmos que a tendência linear existiu antes de 1950 e continua depois de 2000, os valores médios das casas dos dois estados serão (ou foram) iguais em que ano? (A resposta pode ser absurda.)

Aplicativos do mundo real

45) Em 2004, a população escolar era$1001$. Em 2008, a população havia crescido para$1697$. Suponha que a população esteja mudando linearmente.

1. Quanto a população cresceu entre o ano de 2004 e 2008?
2. Quanto tempo a população levou para crescer de$1001$ estudantes para$1697$ estudantes?
3. Qual é o crescimento médio da população por ano?
4. Qual era a população no ano 2000?
5. Encontre uma equação para a população$P$,, dos$t$ anos escolares após 2000.
6. Usando sua equação, preveja a população da escola em 2011.

Responda

1. $696$pessoas
2. $4$anos
3. $174$pessoas por ano
4. $305$pessoas
5. $P(t)=305+174t$
6. $2219$pessoas

46) Em 2003, a população de uma cidade era$1431$. Em 2007, a população havia crescido para$2134$. Suponha que a população esteja mudando linearmente.

1. Quanto a população cresceu entre 2003 e 2007?
2. Quanto tempo a população levou para crescer de$1431$ pessoa para$2134$ pessoa?
3. Qual é o crescimento médio da população por ano?
4. Qual era a população no ano 2000?
5. Encontre uma equação para a população$P$ da cidade$t$ anos após 2000.
6. Usando sua equação, preveja a população da cidade em 2014.

47) Uma companhia telefônica tem um plano celular mensal em que o cliente paga uma taxa mensal fixa e, em seguida, uma certa quantia de dinheiro por minuto usada no telefone. Se um cliente usar$410$ minutos, o custo mensal será$\$71.50$. Se o cliente usar$720$ minutos, o custo mensal será$\$118$.

1. Interprete a inclinação e a$y$ interceptação da equação.
2. Use sua equação para encontrar o custo mensal total se forem usados$687$ minutos.

Responda

1. $C(x)=0.15x+10$
2. A taxa mensal fixa é$\$10$ e há uma$\$0.15$ taxa adicional para cada minuto adicional usado.
3. $\$113.05$

48) Uma companhia telefônica tem um plano mensal de dados celulares em que o cliente paga uma taxa mensal fixa de$\$10$ e, em seguida, uma certa quantia de dinheiro por megabyte (MB) de dados usados no telefone. Se um cliente usar$20$ MB, o custo mensal será$\$11.20$. Se o cliente usar$130$ MB, o custo mensal será$\$17.80$.

1. Interprete a inclinação e a$y$ interceptação da equação.
2. Use sua equação para encontrar o custo mensal total se$250$ MB forem usados.

49) Em 1991, a população de alces em um parque foi medida em$4,360$. Em 1999, a população foi medida novamente como sendo$5,880$. Suponha que a população continue mudando linearmente.

1. O que seu modelo prevê a população de alces em 2003?

Responda

1. $P(t)=190t+4360$
2. $6640$alce

50) Em 2003, a população de corujas em um parque foi medida em$340$. Em 2007, a população foi medida novamente como sendo$285$. A população muda linearmente. Que a contribuição seja de anos desde 1990.

1. Qual é a previsão do seu modelo para a população de corujas em 2012?

51) A Reserva Federal de Hélio continha cerca de$16$ bilhões de pés cúbicos de hélio em 2010 e está sendo esgotada em cerca de$2.1$ bilhões de pés cúbicos a cada ano.

1. Em 2015, quais serão as reservas de hélio?
2. Se a taxa de esgotamento não mudar, em que ano a Reserva Federal de Hélio será esgotada?

Responda

1. $R(t)=16−2.1t$
2. $5.5$bilhões de pés cúbicos
3. Durante o ano de 2017

52) Suponha que as reservas mundiais de petróleo em 2014 sejam$1,820$ bilhões de barris. Se, em média, as reservas totais estão diminuindo em$25$ bilhões de barris de petróleo a cada ano:

1. Daqui a sete anos, quais serão as reservas de petróleo?
2. Se a taxa na qual as reservas estão diminuindo for constante, quando as reservas mundiais de petróleo serão esgotadas?

53) Você está escolhendo entre dois planos de celular pré-pagos diferentes. O primeiro plano cobra uma taxa de$26$ centavos por minuto. O segundo plano cobra uma taxa mensal de$\$19.95$ mais$11$ centavos por minuto. Quantos minutos você precisaria usar em um mês para que o segundo plano fosse preferível?

Responda

Mais de$133$ minutos

54) Você está escolhendo entre duas empresas diferentes de lavagem de janelas. As primeiras cobranças$\$5$ por janela. O segundo cobra uma taxa básica de$\$40$ mais$\$3$ por janela. Quantas janelas você precisaria ter para que a segunda empresa fosse preferível?

55) Quando contratado para um novo emprego vendendo joias, você tem duas opções de pagamento:

Opção A: Salário base de$\$17,000$ um ano com uma comissão$12\%$ de suas vendas
Opção B: salário base de$\$20,000$ um ano com uma comissão$5\%$ de suas vendas

Quantas joias você precisaria vender para a opção A para gerar uma renda maior?

Responda

Mais do que um$\$42,857.14$ valor em joias

56) Quando contratado em um novo emprego na venda de eletrônicos, você tem duas opções de pagamento:

Opção A: salário base de$\$14,000$ um ano com uma comissão$10\%$ de suas vendas

Opção B: salário base de$\$19,000$ um ano com uma comissão$4\%$ de suas vendas

Quantos eletrônicos você precisaria vender para a opção A para gerar uma renda maior?

57) Quando contratado em um novo emprego na venda de eletrônicos, você tem duas opções de pagamento:

Opção A: salário base de$\$20,000$ um ano com uma comissão$12\%$ de suas vendas

Opção B: salário base de$\$26,000$ um ano com uma comissão$3\%$ de suas vendas

Quantos eletrônicos você precisaria vender para a opção A para gerar uma renda maior?

Responda

$\$66,666.67$

58) Quando contratado em um novo emprego na venda de eletrônicos, você tem duas opções de pagamento:

Opção A: salário base de$\$10,000$ um ano com uma comissão$9\%$ de suas vendas

Opção B: salário base de$\$20,000$ um ano com uma comissão$4\%$ de suas vendas

Quantos eletrônicos você precisaria vender para a opção A para gerar uma renda maior?

2.4 Ajustando modelos lineares aos dados

Verbal

1) Descreva o que significa se houver uma falha no modelo ao usar um modelo linear.

Responda

Quando nosso modelo não se aplica mais, depois de algum valor no domínio, o modelo em si não se sustenta.

2) O que é interpolação ao usar um modelo linear?

3) O que é extrapolação ao usar um modelo linear?

Responda

Prevemos um valor fora do domínio e do intervalo dos dados.

4) Explique a diferença entre um coeficiente de correlação positivo e negativo.

5) Explique como interpretar o valor absoluto de um coeficiente de correlação.

Responda

Quanto mais próximo estiver o número$1$, menos dispersos os dados, quanto mais próximo o número estiver$0$, mais dispersos serão os dados.

Algébrico

6) Uma regressão foi executada para determinar se existe uma relação entre horas de TV assistidas por dia (x) e o número de abdominais que uma pessoa pode fazer (y). Os resultados da regressão são apresentados abaixo. Use isso para prever o número de flexões que uma pessoa que assiste$11$ horas de TV pode fazer.

$$\begin{array}{l}{y=a x+b} \\ {a=-1.341} \\ {b=32.234} \\ {r=-0.896}\end{array}\nonumber$$

7) Uma regressão foi executada para determinar se existe uma relação entre o diâmetro de uma árvore ($x$, em polegadas) e a idade da árvore ($y$, em anos). Os resultados da regressão são apresentados abaixo. Use isso para prever a idade de uma árvore com$10$ polegadas de diâmetro. $$\begin{array}{l}{y=a x+b} \\ {a=6.301} \\ {b=-1.044} \\ {r=-0.970}\end{array}\nonumber$$

Responda

$61.966$anos

Para os exercícios 8-11, desenhe um gráfico de dispersão para os dados fornecidos. Os dados parecem estar relacionados linearmente?

8)

0	2	4	6	8	10
—22	—19	—15	—11	—6	—2

9)

1	2	3	4	5	6
46	50	59	75	100	136

Responda

Não

10)

100	250	300	450	600	750
12	12,6	13.1	14	14,5	15.2

11)

1	3	5	7	9	11
1	9	28	65	125	216

Responda

Não

12) Para os dados a seguir, desenhe um gráfico de dispersão. Se quiséssemos saber quando a população chegaria$15,000$, a resposta envolveria interpolação ou extrapolação? Olhe a linha e estime a resposta.

Ano	População
1990	11.500
1995	12.100
2000	12.700
2005	13.000
2010	13.750

13) Para os dados a seguir, desenhe um gráfico de dispersão. Se quiséssemos saber quando a temperatura chegaria$28^{\circ} F$, a resposta envolveria interpolação ou extrapolação? Olhe a linha e estime a resposta.

Temperatura, °F	16	18	20	25	30
Tempo, segundos	46	50	54	55	62

Responda

Interpolação. Sobre$60° F$.

Gráfica

Para os exercícios 14-17, combine cada gráfico de dispersão com uma das quatro correlações especificadas na Figura ab e na Figura cd.

Figura ab Figura cd

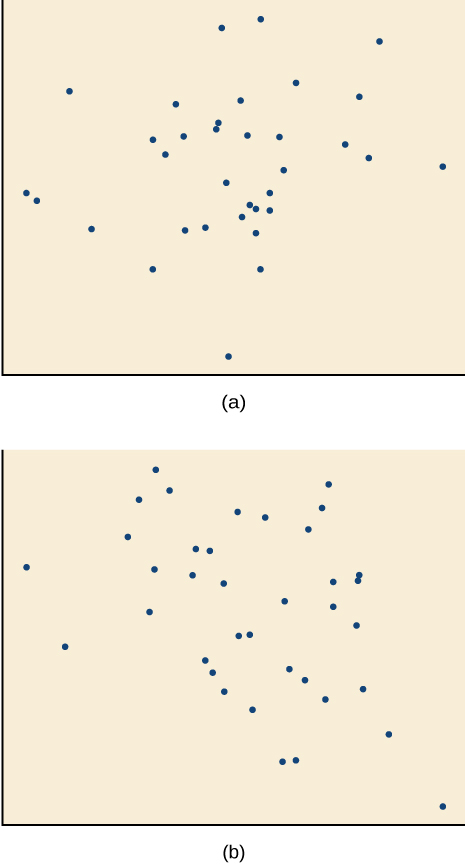
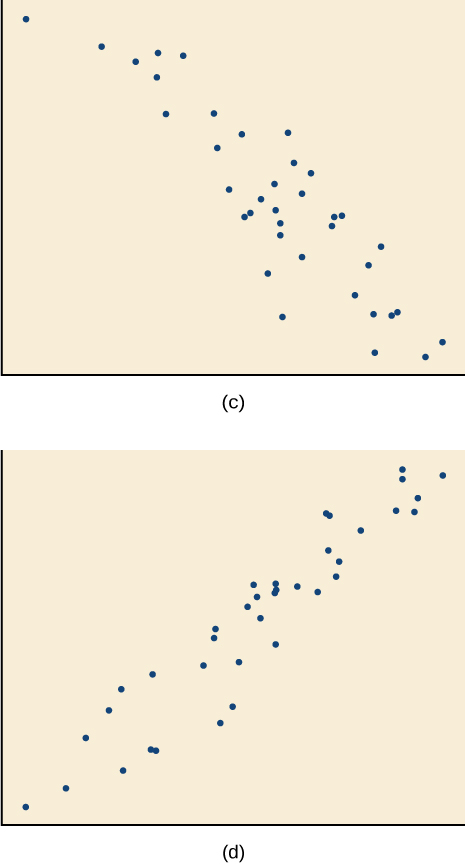
14)$r=0.95$

15)$r=−0.89$

Responda

C

16)$r=0.26$

17)$r=−0.39$

Responda

B

Para os exercícios 18-21, desenhe uma linha de melhor ajuste para os dados plotados.

18)

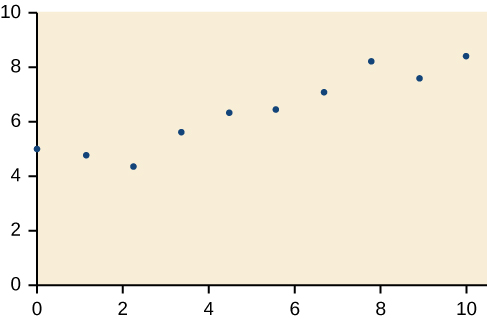
19)

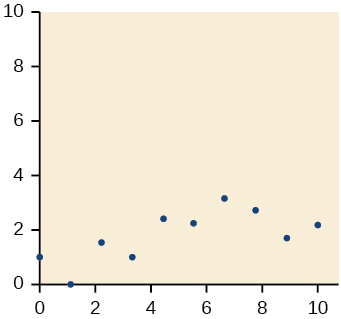
Responda

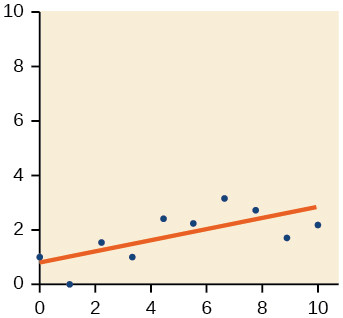
20)

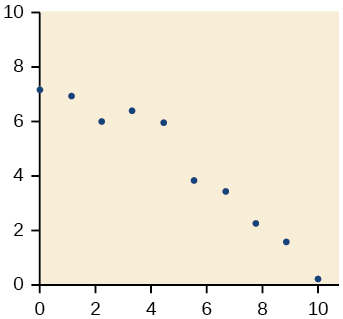
21)

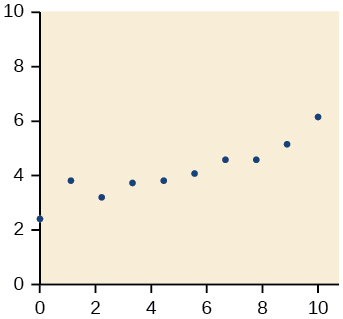
Responda

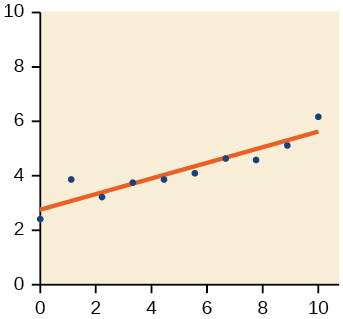
Numérico

22) O Censo dos EUA monitora a porcentagem de pessoas com$25$ anos ou mais que são graduadas. Esses dados de vários anos são fornecidos na Tabela abaixo. Determine se a tendência parece linear. Em caso afirmativo, e supondo que a tendência continue, em que ano a porcentagem excederá$35\%$?

Ano	Percentual de graduados
1990	21.3
1992	21.4
1994	22.2
1996	23,6
1998	24,4
2000	25,6
2002	26,7
2004	27,7
2006	28
2008	29,4

23) A importação americana de vinho (em hectolitros) por vários anos é apresentada na Tabela. Determine se a tendência parece linear. Se sim, e supondo que a tendência continue, em que ano as importações excederão$12,000$ os hectolitros?

Ano	Importações
1992	2665
1994	2688
1996	3565
1998	4129
2000	4584
2002	5655
2004	6549
2006	7950
2008	8487
2009	9462

Responda

Sim, a tendência parece linear porque$r=0.985$ e$12,000$ excederá em meados de 2016,$24.6$ anos desde 1992.

24) A tabela mostra o ano e o número de pessoas desempregadas em uma determinada cidade por vários anos. Determine se a tendência parece linear. Se sim, e supondo que a tendência continue, em que ano o número de desempregados chegará$5$?

Ano	Número de desempregados
1990	750
1992	670
1994	650
1996	605
1998	550
2000	510
2002	460
2004	420
2006	380
2008	320

Tecnologia

Para os exercícios 25-31, use cada conjunto de dados para calcular a linha de regressão usando uma calculadora ou outra ferramenta tecnológica e determine o coeficiente de correlação com$3$ casas decimais de precisão.

25)

$x$	8	15	26	31	56
$y$	23	41	53	72	103

Responda

$y=1.640x+13.800, r=0.987$

26)

$x$	5	7	10	12	15
$y$	4	12	17	22	24

27)

$x$	$y$	$x$	$y$
\ (x\) ">3	\ (y\) ">21,9	\ (x\) ">11	\ (y\) ">15,76
\ (x\) ">4	\ (y\) ">22,22	\ (x\) ">12	\ (y\) ">13,68
\ (x\) ">5	\ (y\) ">22,74	\ (x\) ">13	\ (y\) ">14,1
\ (x\) ">6	\ (y\) ">22,26	\ (x\) ">14	\ (y\) ">14,02
\ (x\) ">7	\ (y\) ">20,78	\ (x\) ">15	\ (y\) ">11,94
\ (x\) ">8	\ (y\) ">17,6	\ (x\) ">16	\ (y\) ">12,76
\ (x\) ">9	\ (y\) ">16,52	\ (x\) ">17	\ (y\) ">11,28
\ (x\) ">10	\ (y\) ">18,54	\ (x\) ">18	\ (y\) ">9,1

Responda

$y=−0.962x+26.86, r=−0.965$

28)

$x$	$y$
\ (x\) ">4	\ (y\) ">44,8
\ (x\) ">5	\ (y\) ">43,1
\ (x\) ">6	\ (y\) ">38,8
\ (x\) ">7	\ (y\) ">39
\ (x\) ">8	\ (y\) ">38
\ (x\) ">9	\ (y\) ">32,7
\ (x\) ">10	\ (y\) ">30,1
\ (x\) ">11	\ (y\) ">29,3
\ (x\) ">12	\ (y\) ">27
\ (x\) ">13	\ (y\) ">25,8

29)

$x$	$y$
\ (x\) ">21	\ (y\) ">17
\ (x\) ">25	\ (y\) ">11
\ (x\) ">30	\ (y\) ">2
\ (x\) ">31	\ (y\) ">−1
\ (x\) ">40	\ (y\) ">−18
\ (x\) ">50	\ (y\) ">−40

Responda

$y=−1.981x+60.197; r=−0.998$

30)

$x$	$y$
\ (x\) ">100	\ (y\) ">2000
\ (x\) ">80	\ (y\) ">1798
\ (x\) ">60	\ (y\) ">1589
\ (x\) ">55	\ (y\) ">1580
\ (x\) ">40	\ (y\) ">1390
\ (x\) ">20	\ (y\) ">1202

31)

$x$	$y$
\ (x\) ">900	\ (y\) ">70
\ (x\) ">988	\ (y\) ">80
\ (x\) ">1000	\ (y\) ">82
\ (x\) ">1010	\ (y\) ">84
\ (x\) ">1200	\ (y\) ">105
\ (x\) ">1205	\ (y\) ">108

Responda

$y=0.121x−38.841, r=0.998$

Extensões

32) Gráfico$f(x)=0.5x+10$. Escolha um conjunto de pares$5$ ordenados usando entradas$x=−2, 1, 5, 6, 9$ e use a regressão linear para verificar se a função é adequada para os dados.

33) Gráfico$f(x)=−2x−10$. Escolha um conjunto de pares$5$ ordenados usando entradas$x=−2, 1, 5, 6, 9$ e use a regressão linear para verificar a função.

Responda

$(−2,−6),(1,−12),(5,−20),(6,−22),(9,−28); y=−2x−10$

Para os exercícios 34-36, considere este cenário: o lucro de uma empresa diminuiu constantemente em um período de dez anos. Os pares ordenados a seguir mostram dólares e o número de unidades vendidas em centenas e o lucro em milhares no período de dez anos (número de unidades vendidas, lucro) para anos registrados específicos:

$$(46, 1,600), (48, 1,550), (50, 1,505), (52, 1,540), (54, 1,495) \nonumber$$

34) Use a regressão linear para determinar uma função$P$ em que o lucro em milhares de dólares depende do número de unidades vendidas em centenas.

35) Encontre até o décimo mais próximo e interprete o$x$ intercepto.

Responda

$(189.8,0)$Se$18,980$ as unidades forem vendidas, a empresa terá um lucro de zero dólares.

36) Encontre até o décimo mais próximo e interprete o$y$ intercepto.

Aplicativos do mundo real

Para os exercícios 37-38, considere este cenário: A população de uma cidade aumentou constantemente ao longo de um período de dez anos. Os pares ordenados a seguir mostram a população e o ano ao longo do período de dez anos (população, ano) para anos registrados específicos:

$$(2500, 2000), (2650, 2001), (3000, 2003), (3500, 2006), (4200, 2010) \nonumber$$

37) Use regressão linear para determinar uma função$y$, em que o ano depende da população. Arredonde para três casas decimais de precisão.

Responda

$y=0.00587x+1985.41$

38) Preveja quando a população atingirá$8,000$.

Para os exercícios 39-40, considere este cenário: o lucro de uma empresa aumentou constantemente em um período de dez anos. Os pares ordenados a seguir mostram o número de unidades vendidas em centenas e o lucro em milhares ao longo do período de dez anos (número de unidades vendidas, lucro) para anos registrados específicos:

$$(46, 250), (48, 305), (50, 350), (52, 390), (54, 410) \nonumber$$

39) Use a regressão linear para determinar uma função$y$, em que o lucro em milhares de dólares depende do número de unidades vendidas em centenas.

Responda

$y=20.25x−671.5$

40) Preveja quando o lucro excederá um milhão de dólares.

Para os exercícios 41-42, considere este cenário: o lucro de uma empresa diminuiu constantemente em um período de dez anos. Os pares pedidos a seguir mostram dólares e o número de unidades vendidas em centenas e o lucro em milhares ao longo de dez anos (número de unidades vendidas, lucro) para anos registrados específicos:

$$(46, 250), (48, 225), (50, 205), (52, 180), (54, 165) \nonumber$$

41) Use a regressão linear para determinar uma função$y$, em que o lucro em milhares de dólares depende do número de unidades vendidas em centenas.

Responda

$y=−10.75x+742.50$

42) Preveja quando o lucro cairá abaixo do$\$25,000$ limite.