2.R: Funções lineares (revisão)

Last updated

Nov 1, 2022
Page ID
189319
Save as PDF
- 2.E: Funções lineares (exercícios)
- 3: Funções polinomiais e racionais

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

2.1 Funções lineares

1) Determine se a equação algébrica é linear: $2 x+3 y=7$

Responda: sim

2) Determine se a equação algébrica é linear: $6 x^{2}-y=5$

3) Determine se a função está aumentando ou diminuindo: $f(x)=7 x-2$

Responda: Aumentando

4) Determine se a função está aumentando ou diminuindo: $g(x)=-x+2$

5) Dado cada conjunto de informações, encontre uma equação linear que satisfaça as condições dadas, se possível. Passa por $(7,5)$ e $(3,17)$

Responda: $y=-3 x+26$

6) Dado cada conjunto de informações, encontre uma equação linear que satisfaça as condições dadas, se possível. $x$ -interceptar em $(6,0)$ e $y$ -interceptar em $(0,10)$

7) Encontre a inclinação da linha mostrada no gráfico de linhas.

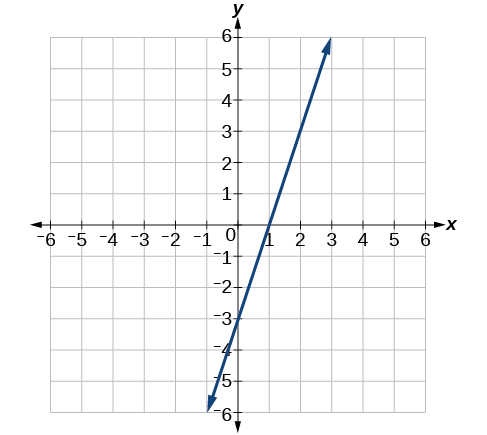
$CNX_Precalc_Figure_02_04_211.jpg$

Responda: $3$

8) Encontre a inclinação da linha representada graficamente.

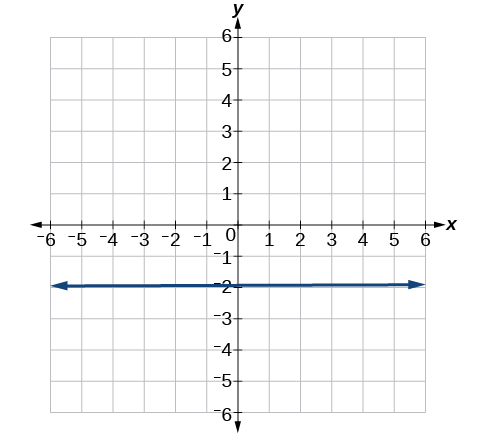
$CNX_Precalc_Figure_02_04_212.jpg$

9) Escreva uma equação na forma de interceptação de inclinação para a linha mostrada.

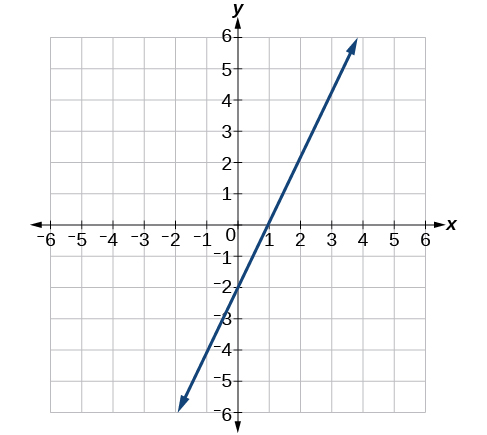
$CNX_Precalc_Figure_02_04_213.jpg$

Responda: $y=2 x-2$

10) A tabela a seguir representa uma função linear? Em caso afirmativo, encontre a equação linear que modela os dados.

$x$	—4	0	2	10
$g(x)$	18	—2	—12	—52

11) A tabela a seguir representa uma função linear? Em caso afirmativo, encontre a equação linear que modela os dados.

$x$	6	8	12	26
$g(x)$	—8	—12	—18	—46

Responda: Não linear

12) Em ^1º de junho, uma empresa tem $\$4,000,000$ lucro. Se a empresa perder $150,000$ dólares por dia a partir de então no mês de junho, qual é o lucro da empresa ^no dia seguinte a ^1º de junho?

2.2 Gráficos de funções lineares

Para os exercícios 1-2, determine se as retas dadas pelas equações abaixo são paralelas, perpendiculares ou nem paralelas nem perpendiculares:

1) $\begin{align*} 2x-6y &=12 \\ -x+3y &=1 \end{align*} \nonumber$

Responda: paralelo

2) $\begin{align*} y &=\dfrac{1}{3} x-2 \\ 3x+y &=-9 \end{align*} \nonumber$

Para os exercícios 3-4, encontre os interceptos $x$ $y$ - e - da equação dada

3) $7 x+9 y=-63$

Responda: $(-9,0); (0,-7)$

4) $f(x)=2 x-1$

Para os exercícios 5-11, use as descrições dos pares de linhas para encontrar as inclinações da Linha 1 e da Linha 2. Cada par de linhas é paralelo, perpendicular ou nenhum dos dois?

Linha 1: passa $(5,11)$ e a $(10,1)$
linha $2 :$ passa por $(-1,3)$ e $(-5,11)$

Responda: Linha 1: $m=-2$ ; Linha 2: $m=-2$ ; Paralela

Linha 1: Passa $(8,-10)$ e $(0,-26)$
Linha 2: Passa por $(2,5)$ e $(4,4)$

7) Escreva uma equação para uma linha perpendicular $f(x)=5 x-1$ e passando pelo ponto $(5,20)$ .

Responda: $y=-0.2 x+21$

8) Encontre a equação de uma reta com um $y$ intercepto de $(0,2)$ e uma inclinação $-\dfrac{1}{2}$ .

9) Esboce um gráfico da função linear $f(t)=2t-5$ .

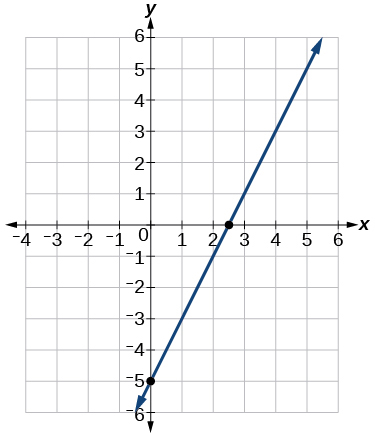
Responda: $CNX_Precalc_Figure_02_04_214.jpg$

10) Encontre o ponto de interseção para as funções $2$ lineares: $\begin{align*} x &=y+6 \\ 2x-y &=13 \end{align*}$

11) Uma locadora de veículos oferece dois planos para alugar um carro.

Plano A: $25$ dólares por dia e $10$ centavos por milha

Plano B: $50$ dólares por dia com quilometragem ilimitada gratuita

Quantas milhas você precisaria dirigir para o plano B para economizar dinheiro?

Responda: $250$

2.3 Modelagem com funções lineares

1) Encontre a área de um triângulo delimitada pelo $y$ eixo, a linha $f(x)=10-2x$ e a linha perpendicular a $f$ que passa pela origem.

2) A população de uma cidade aumenta a uma taxa constante. Em 2010, a população era $55,000$ . Em 2012, a população aumentou para $76,000$ . Se essa tendência continuar, preveja a população em 2016.

Responda: $118,000$

3) O número de pessoas afetadas pelo resfriado comum nos meses de inverno caiu constantemente a $50$ cada ano, desde 2004 até 2010. Em 2004, $875$ pessoas foram infligidas.

4) Encontre a função linear que modela o número de pessoas afetadas pelo $C$ resfriado comum em função do ano, $t$ . Quando ninguém será afligido?

Para os exercícios 5-6, use o gráfico na Figura abaixo mostrando o lucro $y$ , em milhares de dólares, de uma empresa em um determinado ano $x$ , que $x$ representa anos desde 1980.

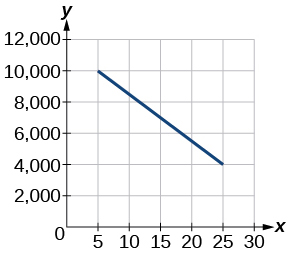
$CNX_Precalc_Figure_02_04_215.jpg$

5) Encontre a função linear $y$ , onde $y$ depende $x$ , do número de anos desde 1980.

Responda: $y=-300 x+11,500$

6) Encontre e interprete o $y$ intercepto.

7) Para o seguinte exercício, considere este cenário: Em 2004, uma população escolar era $1,700$ . Em 2012, a população havia crescido para $2,500$ . Suponha que a população esteja mudando linearmente.

Quanto a população cresceu entre o ano de 2004 e 2012?
Qual é o crescimento médio da população por ano?
Encontre uma equação para a população $P$ ,, dos $t$ anos escolares após 2004.

Responda

$800$
$100$ estudantes por ano
$P(t)=100 t+1700$

Para os exercícios 8-9, considere este cenário: Em 2000, a população de alces em um parque foi medida em $6,500$ . Em 2010, a população foi medida em $12,500$ . Suponha que a população continue mudando linearmente.

8) Encontre uma fórmula para a população de alces, $P$ .

9) O que seu modelo prevê a população de alces em 2020?

Responda: $18,500$

Para os exercícios 10-, considere este cenário: Os valores médios das casas nas subdivisões Pima Central e East Valley (ajustados pela inflação) são mostrados na Tabela abaixo. Suponha que os valores da casa estejam mudando linearmente.

Ano	Pima Central	Vale do Leste
1970	32.000	120.250
2010	85.000	150.000

10) Em qual subdivisão os valores das casas aumentaram a uma taxa mais alta?

11) Se essas tendências continuassem, qual seria o valor médio da casa no Pima Central em 2015?

Responda: $\$91,625$

2.4 Ajustando modelos lineares aos dados

1) Desenhe um gráfico de dispersão para os dados na tabela abaixo. Em seguida, determine se os dados parecem estar relacionados linearmente.

0	2	4	6	8	10
—105	—50	1	55	105	160

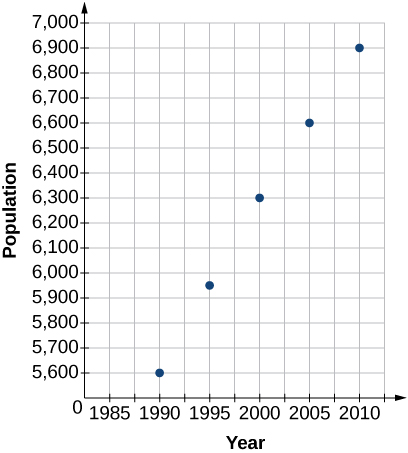
2) Desenhe um gráfico de dispersão para os dados na tabela. Se quiséssemos saber quando a população chegaria $15,000$ , a resposta envolveria interpolação ou extrapolação?

Ano	População
1990	5.600
1995	5.950
2000	6.300
2005	6.600
2010	6.900

Responda

Extrapolação

$CNX_Precalc_Figure_02_04_226.jpg$

3) Oito alunos foram convidados a estimar sua pontuação em um questionário $10$ de 3 pontos. Suas pontuações estimadas e reais são dadas na tabela. Faça um gráfico dos pontos e, em seguida, desenhe uma linha que se ajuste aos dados.

Previsto	Real
6	6
7	7
7	8
8	8
7	9
9	10
10	10
10	9

4) Desenhe uma linha de melhor ajuste para os dados plotados.

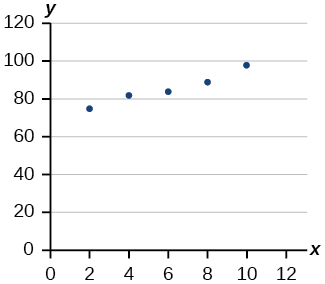
$CNX_Precalc_Figure_02_04_216.jpg$

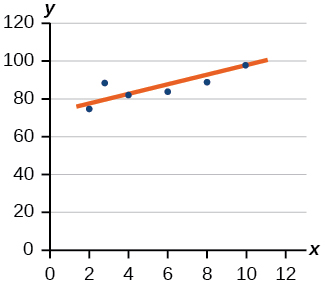
Responda: $CNX_Precalc_Figure_02_04_217.jpg$

Para os exercícios 5-6, considere os dados da Tabela abaixo, que mostra a porcentagem de desempregados em uma cidade de pessoas com $25$ anos ou mais que são graduados universitários, é apresentada abaixo, por ano.

Ano	Percentual de graduados
2000	6.5
2002	7.0
2005	7.4
2007	8.2
2010	9.0

5) Determine se a tendência parece ser linear. Se sim, e supondo que a tendência continue, encontre um modelo de regressão linear para prever a porcentagem de desempregados em um determinado ano com três casas decimais.

6) Em que ano a porcentagem excederá $12\%$ ?

Responda: No meio de 2024

7) Com base no conjunto de dados fornecido na Tabela, calcule a linha de regressão usando uma calculadora ou outra ferramenta tecnológica e determine o coeficiente de correlação com três casas decimais.

$x$	17	20	23	26	29
$y$	15	25	31	37	40

8) Com base no conjunto de dados fornecido na Tabela, calcule a linha de regressão usando uma calculadora ou outra ferramenta tecnológica e determine o coeficiente de correlação com três casas decimais.

$x$	10	12	15	18	20
$y$	36	34	30	28	22

Responda: $y=-1.294 x+49.412; r=-0.974$

Para os exercícios 9-12, considere este cenário: A população de uma cidade aumentou constantemente ao longo de um período de dez anos. Os seguintes pares ordenados mostram a população e o ano ao longo do período de dez anos (população, ano) para anos registrados específicos: $(3,600,2000) ;(4,000,2001) ;(4,700,2003) ;(6,000,2006)$

9) Use regressão linear para determinar uma função $y$ , em que o ano depende da população, com três casas decimais de precisão.

10) Preveja quando a população atingirá $12,000$ .

Responda: No início de 2022

11) Qual é o coeficiente de correlação desse modelo com três casas decimais de precisão?

12) De acordo com o modelo, qual é a população em 2014?

Responda: $7,660$

Teste prático

1) Determine se a seguinte equação algébrica pode ser escrita como uma função linear: $2 x+3 y=7$

Responda: sim

2) Determine se a função a seguir está aumentando ou diminuindo: $f(x)=-2 x+5$

3) Determine se a função a seguir está aumentando ou diminuindo: $f(x)=7 x+9$

Responda: Aumentando

4) Dado o seguinte conjunto de informações, encontre uma equação linear que satisfaça as condições, se possível. Passa por $(5,1)$ e $(3,-9)$

5) Dado o seguinte conjunto de informações, encontre uma equação linear que satisfaça as condições, se possível. $x$ interceptar em $(-4,0)$ e $y$ -interceptar em $(0,-6)$

Responda: $y=-1.5 x-6$

6) Encontre a inclinação da linha na Figura abaixo.

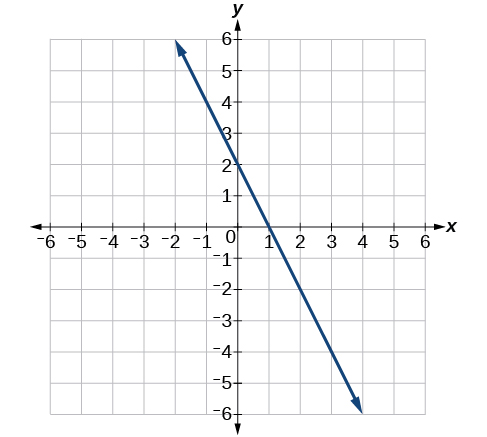
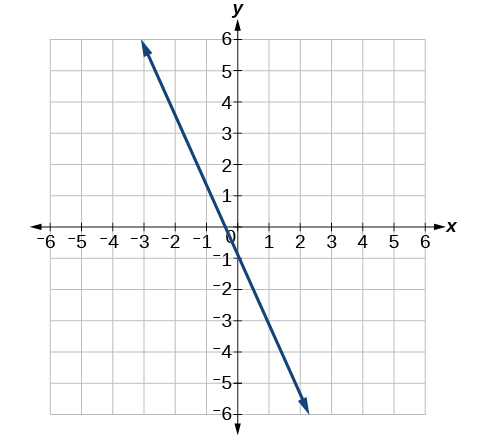
$CNX_Precalc_Figure_02_04_219.jpg$

Responda: $y=-2 x-1$

8) A tabela representa uma função linear? Em caso afirmativo, encontre uma equação linear que modela os dados.

$x$	—6	0	2	4
$g(x)$	14	32	38	44

9) A tabela representa uma função linear? Em caso afirmativo, encontre uma equação linear que modela os dados.

$x$	1	3	7	11
$g(x)$	4	9	19	12

Responda: Não

10) Às 6 da manhã, uma empresa on-line vendeu $120$ itens naquele dia. Se a empresa vender uma média de $30$ itens por hora durante o restante do dia, escreva uma expressão para representar o número de itens que foram vendidos $n$ após as 6h.

Para os exercícios 11-22, determine se as retas dadas pelas equações abaixo são paralelas, perpendiculares ou nem paralelas nem perpendiculares:

11) $\begin{align*}{y=\dfrac{3}{4} x-9} \\ {-4 x-3 y=8}\end{align*}$

Responda: Perpendicular

12) $\begin{align*}{-2 x+y=3} \\ {3 x+\dfrac{3}{2} y=5}\end{align*}$

13) Encontre os $y$ interceptos $x$ - e -da equação $2 x+7 y=-14$ .

Responda: $(-7,0) ;(0,-2)$

14) Abaixo estão as descrições de duas linhas. Encontre as inclinações da Linha 1 e da Linha 2. O par de retas é paralelo, perpendicular ou nenhum dos dois?

A linha $1 :$ passa $(-2,-6)$ e a $(3,14)$
linha $2 :$ passa por $(2,6)$ e $(4,14)$

15) Escreva uma equação para uma linha perpendicular $f(x)=4 x+3$ e passando pelo ponto $(8,10)$ .

Responda: $y=-0.25 x+12$

16) Desenhe uma linha com um $y$ intercepto de $(0,5)$ e uma inclinação $-\dfrac{5}{2}$ .

17) Gráfico da função linear $f(x)=-x+6$ .

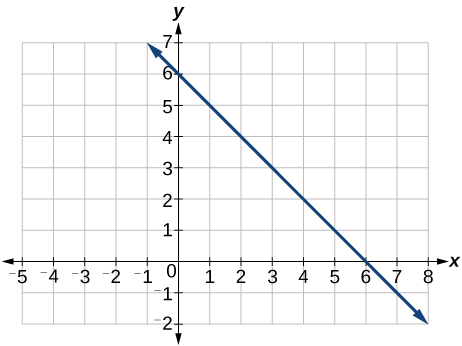
Responda: $CNX_Precalc_Figure_02_04_221.jpg$

18) Para as duas funções lineares, encontre o ponto de interseção: $\begin{align*} x &=y+2 \\ 2x-3y &=-1 \end{align*}$

19) Uma locadora de veículos oferece dois planos para alugar um carro.

Plano A: $\$ 25$ por dia e $\$ 0.10$ por milha
Plano B: $\$ 40$ por dia com quilometragem gratuita ilimitada

Quantas milhas você precisaria dirigir para o plano B para economizar dinheiro?

Responda: $150$

20) Encontre a área de um triângulo delimitada pelo $y$ eixo, a linha $f(x)=12-4 x,$ e a linha perpendicular a $f$ que passa pela origem.

21) A população de uma cidade aumenta a uma taxa constante. Em 2010, a população era $65,000$ . Em 2012, a população aumentou para $90,000$ . Supondo que essa tendência continue, preveja a população em 2018.

Responda: $165,000$

22) O número de pessoas afetadas pelo resfriado comum nos meses de inverno caiu constantemente a $25$ cada ano, desde 2002 até 2012. Em 2002, $8,040$ pessoas foram infligidas. Encontre a função linear que modela o número de pessoas afetadas pelo $C$ resfriado comum em função do ano, $t$ . Quando menos de $6,000$ pessoas serão afligidas?

Para os exercícios 23-24, use o gráfico na Figura, mostrando o lucro $y$ , em milhares de dólares, de uma empresa em um determinado ano $x$ , que $x$ representa anos desde 1980.

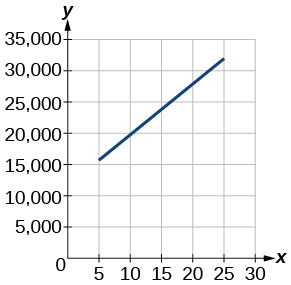
$CNX_Precalc_Figure_02_04_222.jpg$

23) Encontre a função linear $y$ , onde $y$ depende $x$ , do número de anos desde 1980.

Responda: $y=875 x+10,675$

24) Encontre e interprete o $y$ intercepto.

25) Em 2004, a população escolar era $1250$ . Em 2012, a população havia caído para $875$ . Suponha que a população esteja mudando linearmente.

Quanto a população caiu entre o ano de 2004 e 2012?
Qual é o declínio médio da população por ano?
Encontre uma equação para a população $P$ ,, dos $t$ anos escolares após 2004.

Responda

$375$
caiu uma média de $46.875,$ ou cerca de $47$ pessoas por ano
$y=-46.875 t+1250$

26) Desenhe um gráfico de dispersão para os dados fornecidos na Tabela. Em seguida, determine se os dados parecem estar relacionados linearmente.

0	2	4	6	8	10
—450	—200	10	265	500	755

27) Desenhe uma linha de melhor ajuste para os dados plotados.

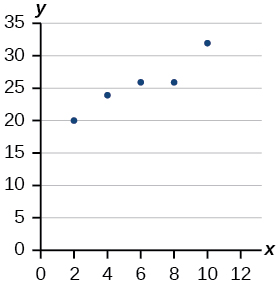
$CNX_Precalc_Figure_02_04_223.jpg$

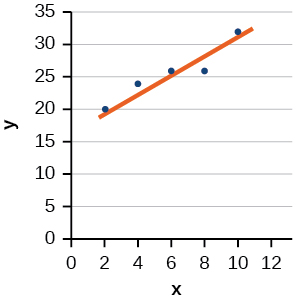
Responda: $CNX_Precalc_Figure_02_04_224.jpg$

Para os exercícios 28-29, use a Tabela abaixo, que mostra a porcentagem de pessoas desempregadas com $25$ anos ou mais que são graduadas em uma determinada cidade, por ano.

Ano	Percentual de graduados
2000	8.5
2002	8.0
2005	7.2
2007	6.7
2010	6.4

28) Determine se a tendência parece linear. Se sim, e supondo que a tendência continue, encontre um modelo de regressão linear para prever a porcentagem de desempregados em um determinado ano com três casas decimais.

29) Em que ano o percentual cairá abaixo $4\%$ ?

Responda: No início de 2018

30) Com base no conjunto de dados fornecido na Tabela abaixo, calcule a linha de regressão usando uma calculadora ou outra ferramenta tecnológica e determine o coeficiente de correlação. Arredonde para três casas decimais de precisão.

$x$	16	18	20	24	26
$y$	106	110	115	120	125

Para os exercícios 31-33, considere este cenário: A população de uma cidade aumentou constantemente ao longo de um período de dez anos. Os pares ordenados a seguir mostram a população (em centenas) e o ano durante o período de dez anos (população, ano) para anos registrados específicos: $(4,500,2000) ;(4,700,2001) ;(5,200,2003) ;(5,800,2006)$

31) Use regressão linear para determinar uma função y, em que o ano depende da população. Arredonde para três casas decimais de precisão.

Responda: $y=0.00455 x+1979.5$

32) Preveja quando a população atingirá $20,000$ .

33) Qual é o coeficiente de correlação para esse modelo?

Responda: $r=0.999$