B: Fundamentos matemáticos
- Page ID
- 181650
Quadrados e outros poderes
Um expoente, ou uma potência, é uma abreviatura matemática para multiplicações repetidas. Por exemplo, o expoente “2” significa multiplicar a base desse expoente por si só (no exemplo aqui, a base é “5”):
\[5^2=5×5=25\]
O expoente é “2” e a base é o número “5". Essa expressão (multiplicando um número por si só) também é chamada de quadrado. Qualquer número elevado à potência de 2 está sendo quadrado. Qualquer número elevado à potência de 3 está sendo reduzido ao cubo:
\[5^3=5×5×5=125\]
Um número elevado à quarta potência é igual a esse número multiplicado por si mesmo quatro vezes, e assim por diante para potências superiores. Em geral:
\[n^x=n×n^{x−1}\]
Calculando porcentagens
Um percentual é uma forma de expressar uma quantidade fracionária de algo usando um todo dividido em 100 partes. Uma porcentagem é uma proporção cujo denominador é 100. Usamos o símbolo de porcentagem,%, para mostrar a porcentagem. Assim, 25% significa uma proporção de\(\frac{25}{100}\), 3% significa uma proporção de\(\frac{3}{100}\), e 100% por cento significa\(\frac{100}{100}\), ou um todo.
Conversão de porcentagens
Uma porcentagem pode ser convertida em uma fração escrevendo o valor da porcentagem como uma fração com um denominador de 100 e simplificando a fração, se possível.
\[25\%=\dfrac{25}{100}=\dfrac{1}{4}\]
Uma porcentagem pode ser convertida em decimal escrevendo o valor da porcentagem como uma fração com um denominador de 100 e dividindo o numerador pelo denominador.
\[10\%=\dfrac{10}{100}=0.10\]
Para converter um decimal em um percentual, escreva o decimal como uma fração. Se o denominador da fração não for 100, converta-o em uma fração com um denominador de 100 e, em seguida, escreva a fração como uma porcentagem.
\[0.833=\dfrac{833}{1000}=\dfrac{83.3}{100}=83.3\%\]
Para converter uma fração em porcentagem, primeiro converta a fração em decimal e, em seguida, converta o decimal em um percentual.
\[\dfrac{3}{4}=0.75=\dfrac{75}{100}=75\%\]
Suponha que um pesquisador descubra que 15 dos 23 alunos de uma turma são portadores de Neisseria meningitides. Qual porcentagem de estudantes são portadores? Para encontrar esse valor, primeiro expresse os números como uma fração.
\[\mathrm{\dfrac{carriers}{total\: students}}=\dfrac{15}{23}\]
Em seguida, divida o numerador pelo denominador.
\[\dfrac{15}{23}=15\div 23 \approx 0.65\]
Finalmente, para converter um decimal em um percentual, multiplique por 100.
\[0.65 \times 100=65\%\]
A porcentagem de estudantes que são portadores é de 65%.
Você também pode obter dados sobre ocorrência e não ocorrência; por exemplo, em uma amostra de estudantes, 9 testaram positivo para anticorpos para Toxoplasma, enquanto 28 testaram negativo. Qual é a porcentagem de estudantes soropositivos? O primeiro passo é determinar o “todo”, do qual os estudantes positivos fazem parte. Para fazer isso, some os testes positivos e negativos.
\[\mathrm{positive+negative=9+28=37}\]
A amostra total foi composta por 37 estudantes. A fração de pontos positivos é:
\[\mathrm{\dfrac{positive}{total\: students}=\dfrac{9}{37}}\]
Para encontrar a porcentagem de estudantes que são portadores, divida o numerador pelo denominador e multiplique por 100.
\ [\ dfrac {9} {37} =9\ div 37\ aproximadamente 0,24\\
0,24\ times 100=24\%\]
A porcentagem de estudantes positivos é de cerca de 24%.
Outra forma de pensar em calcular uma porcentagem é configurar frações equivalentes, uma das quais é uma fração com 100 como denominador, e multiplicar cruzadamente. O exemplo anterior seria expresso como:
\[\dfrac{9}{37}=\dfrac{x}{100}\]
Agora, multiplique e resolva o desconhecido:
\ [\ begin {align}
9\ times 100 &=37 x & &\ nonumber\\ [5pt]
\ frac {9\ times 100} {37} &=x & &\ text {Divida os dois lados por 37}\ nonumber\\ [5pt]\ frac {900} {37} &=x & &\ text {Multiplicar}
\ nonumber\\ [5pt]\ frac {900} {37} &=x & &\ text {Multiplique}\ nonumber\\ [5pt]
&\ aprox. x & &\ text {Dividir}\ nonumber
\ end {align}\]
A resposta, arredondada, é a mesma.
Multiplicação e divisão por dezenas
Em muitos campos, especialmente nas ciências, é comum multiplicar decimais por potências de 10. Vamos ver o que acontece quando multiplicamos 1,9436 por algumas potências de 10.
\ [\ begin {align}
1.9436 (10) &=19.436\ nonumber\\
1.9436 (100) &=194,36\ nonumber\\
1.9436 (1000) &=1943.6\ nonumber
\ end {align}\]
O número de casas que o ponto decimal se move é o mesmo que o número de zeros na potência de dez. A tabela\(\PageIndex{1}\) resume os resultados.
| Multiplique por | Zeros | Movimentos de ponto decimal. |
|---|---|---|
| 10 | 1 | 1 lugar à direita |
| 100 | 2 | 2 lugares à direita |
| 1.000 | 3 | 3 lugares à direita |
| 10.000 | 4 | 4 lugares à direita |
Podemos usar esse padrão como um atalho para multiplicar por potências de dez em vez de multiplicar usando o formato vertical. Podemos contar os zeros na potência de 10 e depois mover o ponto decimal com o mesmo número de casas para a direita.
Então, por exemplo, para multiplicar 45,86 por 100, mova o ponto decimal 2 casas para a direita.
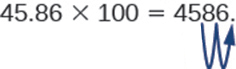
Às vezes, quando precisamos mover o ponto decimal, não há casas decimais suficientes. Nesse caso, usamos zeros como espaços reservados. Por exemplo, vamos multiplicar 2,4 por 100. Precisamos mover o ponto decimal 2 casas para a direita. Como há apenas um dígito à direita do ponto decimal, devemos escrever um 0 na casa dos centésimos.
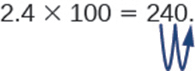
Ao dividir por potências de 10, simplesmente adote a abordagem oposta e mova o decimal para a esquerda pelo número de zeros na potência de dez.
Vamos ver o que acontece quando dividimos 1,9436 por algumas potências de 10.
\ [\ begin {align}
1.9436\ div 10&=0,19436\ nonumber\\
1.9436\ div 100&=0.019436\ nonumber\\
1.9436\ div 1000&=0,0019436\ nonumber
\ end {align}\]
Se não houver dígitos suficientes para mover o decimal, adicione zeros para criar casas.
Notação científica
A notação científica é usada para expressar números muito grandes e muito pequenos como um produto de dois números. O primeiro número do produto, o termo do dígito, geralmente é um número não inferior a 1 e não maior que 10. O segundo número do produto, o termo exponencial, é escrito como 10 com um expoente. Alguns exemplos de notação científica são apresentados na Tabela\(\PageIndex{2}\).
| Notação padrão | Notação científica |
|---|---|
| 1000 | 1 × 10 3 |
| 100 | 1 × 10 2 |
| 10 | 1 × 10 1 |
| 1 | 1 × 10 0 |
| 0.1 | 1 × 10 −1 |
| 0,01 | 1 × 10 −2 |
A notação científica é uma notação particularmente útil para números muito grandes e muito pequenos, como 1.230.000.000 = 1,23 × 10 9 e 0,000000036 = 3,6 × 10 −10.
Expressando números em notação científica
A conversão de qualquer número em notação científica é simples. Conte o número de casas necessárias para mover o decimal ao lado do dígito diferente de zero na extremidade esquerda: ou seja, para colocar o número entre 1 e 10. Em seguida, multiplique esse número por 10 elevado ao número de casas em que você moveu o decimal. O expoente é positivo se você mover o decimal para a esquerda e negativo se você mover o decimal para a direita. Então
\[2386=2.386\times1000=2.386\times10^3\]
e
\[0.123=1.23\times0.1=1.23\times10^{-1}\]
A potência (expoente) de 10 é igual ao número de casas em que o decimal é deslocado.
Logaritmos
O logaritmo comum (log) de um número é a potência à qual 10 deve ser aumentado para igualar esse número. Por exemplo, o logaritmo comum de 100 é 2, porque 10 deve ser elevado à segunda potência para ser igual a 100. Exemplos adicionais estão na Tabela\(\PageIndex{3}\).
| Número | Forma exponencial | Logaritmo comum |
|---|---|---|
| 1000 | 10 3 | 3 |
| 10 | 10 1 | 1 |
| 1 | 10 0 | 0 |
| 0.1 | 10 −1 | −1 |
| 0,001 | 10 −3 | −3 |
Para encontrar o logaritmo comum da maioria dos números, você precisará usar o botão LOG em uma calculadora.
Arredondamento e dígitos significativos
Ao relatar dados numéricos obtidos por meio de medições, usamos apenas tantos números significativos quanto a precisão da medição garante. Por exemplo, suponha que um microbiologista usando um contador de células automatizado determine que há 525.341 células bacterianas em uma amostra de um litro de água do rio. No entanto, ela registra a concentração em 525.000 células por litro e usa esse número arredondado para estimar o número de células que provavelmente seriam encontradas em 10 litros de água do rio. Nesse caso, os últimos três dígitos da quantidade medida não são considerados significativos. Eles são arredondados para levar em conta as variações no número de células que provavelmente ocorreriam se mais amostras fossem medidas.
A importância de números significativos está em sua aplicação à computação fundamental. Além da adição e subtração, a soma ou diferença deve conter tantos dígitos à direita do decimal quanto o menos certo (indicado por sublinhado no exemplo a seguir) dos números usados no cálculo.
Suponha que um microbiologista deseje calcular a massa total de duas amostras de ágar.
\ [\ begin {array} {l}
4.38\ sublinhado {3}\ texto {g}\
\ sublinhado {3.002\ sublinhado {1}}\ texto {g}\
7.38\ sublinhado {5}\ texto {g}
\ end {array}\]
A menor das duas massas tem três casas decimais, então a soma deve ter três casas decimais.
Na multiplicação e divisão, o produto ou quociente não deve conter mais dígitos do que o fator que contém o menor número de números significativos. Suponha que o microbiologista queira calcular quanto de um reagente estaria presente em 6,6 mL se a concentração fosse 0,638 g/mL.
\[\mathrm{0.63\underline{8}\:\dfrac{g}{mL}\times6.\underline{6}\:mL=4.1\:g}\]
Novamente, a resposta tem apenas uma casa decimal porque essa é a precisão do número menos preciso no cálculo.
Ao arredondar números, aumente o dígito retido em 1 se ele for seguido por um número maior que 5 (“arredondar para cima”). Não altere o dígito retido se os dígitos seguintes forem menores que 5 (“arredondar para baixo”). Se o dígito retido for seguido por 5, arredonde para cima se o dígito retido for ímpar ou para baixo se for par (após o arredondamento, o dígito retido sempre será par).
Tempo de geração
É possível escrever uma equação para calcular os números das células a qualquer momento se o número de células iniciais e o tempo de duplicação forem conhecidos, desde que as células estejam se dividindo a uma taxa constante. Definimos N 0 como o número inicial de bactérias, o número no tempo t = 0. N i é o número de bactérias no tempo t = i, um momento arbitrário no futuro. Finalmente, definiremos j igual ao número de gerações, ou o número de vezes que a população celular dobra durante o intervalo de tempo. Então nós temos,
\[N_i=N_0\times2^j\]
Essa equação é uma expressão do crescimento por fissão binária.
Em nosso exemplo, N 0 = 4, o número de gerações, j, é igual a 3 após 90 minutos porque o tempo de geração é de 30 minutos. O número de células pode ser estimado a partir da seguinte equação:
\ [\ begin {align}
N_i&=N_0\ times2^j\ nonumber\\
N_ {90} &=4\ times2^3\ nonumber\\
N_ {90} &=4\ times8=32\ nonumber
\ end {align}\]
O número de células após 90 minutos é 32.
Número mais provável
A tabela na Figura\(\PageIndex{1}\) contém valores usados para calcular o exemplo de número mais provável dado em Como os micróbios crescem.