2.8: Desigualdades lineares e de valor absoluto
- Page ID
- 189263
- Use a notação de intervalo.
- Use as propriedades das desigualdades.
- Resolva as desigualdades em uma variável algebricamente.
- Resolva desigualdades de valor absoluto.
Não é fácil assumir o papel de honra na maioria das melhores universidades. Suponha que os alunos sejam obrigados a carregar uma carga horária de pelo menos horas de\(12\) crédito e manter uma média de notas\(3.5\) igual ou superior. Como esses requisitos do quadro de honra poderiam ser expressos matematicamente? Nesta seção, exploraremos várias maneiras de expressar diferentes conjuntos de números, desigualdades e desigualdades de valor absoluto.

Usando notação de intervalo
Indicar a solução para uma desigualdade como a que\(x≥4\) pode ser alcançada de várias maneiras.
- Podemos usar uma linha numérica conforme mostrado na Figura\(\PageIndex{2}\). O raio azul começa em\(x = 4\) e, conforme indicado pela ponta da seta, continua até o infinito, o que ilustra que o conjunto de soluções inclui todos os números reais maiores ou iguais\(4\) a.
- Podemos usar a notação set-builder:\(\{x|x≥4\}\), que se traduz em “todos os números reais\(x\) que\(x\) sejam maiores ou iguais a”\(4\). Observe que colchetes são usados para indicar um conjunto.
- O terceiro método é a notação de intervalo, na qual os conjuntos de soluções são indicados com parênteses ou colchetes. As soluções do\(x≥4\) são representadas como\([4,\infty)\). Esse talvez seja o método mais útil, pois se aplica aos conceitos estudados posteriormente neste curso e a outros cursos de matemática de nível superior.

O principal conceito a ser lembrado é que parênteses representam soluções maiores ou menores que o número, e colchetes representam soluções maiores ou iguais ou menores ou iguais ao número. Use parênteses para representar infinito ou infinito negativo, já que infinito positivo e negativo não são números no sentido usual da palavra e, portanto, não podem ser “igualados”. Alguns exemplos de um intervalo ou conjunto de números no qual uma solução cai são\([−2,6)\), ou todos os números entre\(−2\) e\(6\), incluindo\(−2\), mas não incluindo\(6\);\((−1,0)\), todos os números reais entre, mas não incluindo\(−1\) e\(0\); e\((−\infty,1]\), todos reais números menores que e inclusive\(1\). A tabela\(\PageIndex{1}\) descreve as possibilidades.
| Conjunto indicado | Notação Set-Builder | Notação de intervalo |
|---|---|---|
| Todos os números reais entre\(a\) e\(b\), mas não incluindo\(a\) ou\(b\) | \(\{x|a<x<b\}\) | \((a,b)\) |
| Todos os números reais são maiores que\(a\), mas não incluindo\(a\) | \(\{x|x>a\}\) | \((a,\infty)\) |
| Todos os números reais menores que\(b\), mas não incluindo\(b\) | \(\{x|x<b\}\) | \((−\infty,b)\) |
| Todos os números reais maiores que\(a\), incluindo\(a\) | \(\{x|x≥a\}\) | \([a,\infty)\) |
| Todos os números reais menores que\(b\), incluindo\(b\) | \(\{x|x≤b\}\) | \((−\infty,b]\) |
| Todos os números reais entre\(a\) e\(b\), incluindo\(a\) | \(\{x|a≤x<b\}\) | \([a,b)\) |
| Todos os números reais entre\(a\) e\(b\), incluindo\(b\) | \(\{x|a<x≤b\}\) | \((a,b]\) |
| Todos os números reais entre\(a\) e\(b\), incluindo\(a\) e\(b\) | \(\{x|a≤x≤b\}\) | \([a,b]\) |
| Todos os números reais menores\(a\) ou maiores que\(b\) | \(\{x|x<a\space and\space x>b\}\) | \((−\infty,a)\cup(b,\infty)\) |
| Todos os números reais | \(\{x|x\space is\space all\space real\space numbers\}\) | \((−\infty,\infty)\) |
Use a notação de intervalo para indicar todos os números reais maiores ou iguais\(−2\) a.
Solução
Use um colchete à esquerda\(−2\) e parênteses após o infinito:\([−2,\infty)\). O colchete indica que\(−2\) está incluído no conjunto com todos os números reais maiores que\(−2\) o infinito.
Use a notação de intervalo para indicar todos os números reais entre\(−3\) e incluindo\(5\) e.
- Responda
-
\([−3,5]\)
Escreva o intervalo expressando todos os números reais menores\(−1\) ou iguais ou maiores ou iguais\(1\) a.
Solução
Temos que escrever dois intervalos para este exemplo. O primeiro intervalo deve indicar todos os números reais menores ou iguais\(1\) a. Então, esse intervalo começa em\(−\infty\) e termina em\(−1\), o que é escrito como\((−\infty,−1]\).
O segundo intervalo deve mostrar todos os números reais maiores ou iguais a\(1\), que são escritos como\([1,\infty)\). No entanto, queremos combinar esses dois conjuntos. Conseguimos isso inserindo o símbolo da união,, entre os dois intervalos.
\[(−\infty,−1]\cup[1,\infty) \nonumber\]
Expresse todos os números reais menores\(−2\) ou maiores ou iguais a\(3\) em notação de intervalo.
- Responda
-
\((−\infty,−2)\cup[3,\infty)\)
Usando as propriedades das desigualdades
Quando trabalhamos com desigualdades, geralmente podemos tratá-las da mesma forma, mas não exatamente como tratamos as igualdades. Podemos usar a propriedade de adição e a propriedade de multiplicação para nos ajudar a resolvê-las. A única exceção é quando multiplicamos ou dividimos por um número negativo; isso inverte o símbolo de desigualdade.
Propriedade de adição
- Se\(a<b\), então\(a+c<b+c\).
Propriedade de multiplicação
- Se\(a<b\) e\(c>0\), então\(ac<bc\).
- Se\(a<b\) e\(c<0\), então\(ac>bc\).
Essas propriedades também se aplicam a\(a≤b\)\(a>b\),\(a≥b\) e.
Ilustre a propriedade de adição para desigualdades resolvendo cada uma das seguintes opções:
- (uma)\(x−15<4\)
- (b)\(6≥x−1\)
- (c)\(x+7>9\)
Solução
A propriedade de adição para desigualdades afirma que, se existir uma desigualdade, adicionar ou subtrair o mesmo número em ambos os lados não altera a desigualdade.
uma.
\[\begin{align*} x-15&< 4\\ x-15+15&< 4+15\\ x&< 19 \end{align*}\]
b.
\[\begin{align*} 6&\geq x-1\\ 6+1&\geq x-1+1\\ 7&\geq x \end{align*}\]
c.
\[\begin{align*} x+7&> 9\\ x+7-7&> 9-7\\ x&> 2 \end{align*}\]
Resolver:\(3x−2<1\).
- Responda
-
\(x<1\)
Ilustre a propriedade de multiplicação das desigualdades resolvendo cada uma das seguintes opções:
- \(3x<6\)
- \(−2x−1≥5\)
- \(5−x>10\)
Solução
uma.
\[\begin{align*} 3x&< 6\\ \dfrac{1}{3}(3x)&< (6)\dfrac{1}{3}\\ x&< 2 \end{align*}\]
b.
\[\begin{align*} -2x-1&\geq 5\\ -2x&\geq 6\\ \left (-\dfrac{1}{2} \right )(-2)&\geq (6)\left (-\dfrac{1}{2} \right ) & & \text{Multiply by } \left (-\dfrac{1}{2} \right )\\ x&\leq -3 & & \text{Reverse the inequality.} \end{align*}\]
c.
\[\begin{align*} 5-x&> 10\\ -x&> 5\\ (-1)(-x)&> (5)(-1) & & \text{Multiply by } -1\\ x&< -5 & & \text{Reverse the inequality.} \end{align*}\]
Resolver:\(4x+7≥2x−3\).
- Responda
-
\(x≥−5\)
Resolvendo desigualdades em uma variável algebricamente
Como os exemplos mostraram, podemos realizar as mesmas operações em ambos os lados de uma desigualdade, assim como fazemos com equações; combinamos termos semelhantes e realizamos operações. Para resolver, isolamos a variável.
Resolva a desigualdade:\(13−7x≥10x−4\).
Solução
Resolver essa desigualdade é semelhante a resolver uma equação até a última etapa.
\[\begin{align*} 13-7x&\geq 10x-4\\ 13-17x&\geq -4 & & \text{Move variable terms to one side of the inequality}\\ -17x&\geq -17 & & \text{Isolate the variable term}\\ x&\leq 1 & & \text{Dividing both sides by -17 reverses the inequality.} \end{align*}\]
O conjunto de soluções é dado pelo intervalo\((−\infty,1]\) ou por todos os números reais menores que e inclusive\(1\).
Resolva a desigualdade e escreva a resposta usando a notação de intervalo:\(−x+4<\dfrac{1}{2}x+1\).
- Responda
-
\((2,\infty)\)
Resolva a seguinte desigualdade e escreva a resposta em notação de intervalo:\(−\dfrac{3}{4}x≥−\dfrac{5}{8}+\dfrac{2}{3}x\).
Solução
Começamos a resolver da mesma forma que fazemos quando resolvemos uma equação.
\[\begin{align*} -\dfrac{3}{4}x&\geq -\dfrac{5}{8}+\dfrac{2}{3}x\\[5pt] -\dfrac{3}{4}x-\dfrac{2}{3}x&\geq -\dfrac{5}{8} & & \text{Put variable terms on one side.}\\[5pt] -\dfrac{9}{12}x-\dfrac{8}{12}x&\geq -\dfrac{5}{8} & & \text{Write fractions with common denominator.}\\[5pt] -\dfrac{17}{12}x&\geq -\dfrac{5}{8}\\[5pt] x&\leq -\dfrac{5}{8}\left (-\dfrac{12}{17} \right ) & & \text{Multiplying by a negative number reverses the inequality.}\\[5pt] x&\leq \dfrac{15}{34} \end{align*}\]
O conjunto de soluções é o intervalo\(\left (−\infty,\dfrac{15}{34} \right ]\).
Resolva a desigualdade e escreva a resposta em notação de intervalo:\(−\dfrac{5}{6}x≤\dfrac{3}{4}+\dfrac{8}{3}x\).
- Responda
-
\(\left [-\dfrac{3}{14},\infty \right )\)
Compreendendo desigualdades compostas
Uma desigualdade composta inclui duas desigualdades em uma declaração. Uma afirmação como\(4<x≤6\) médias\(4<x\) e\(x≤6.\) Existem duas maneiras de resolver desigualdades compostas: separá-las em duas desigualdades separadas ou deixar a desigualdade composta intacta e realizar operações em todas as três partes ao mesmo tempo. Ilustraremos os dois métodos.
Resolva a desigualdade composta:\(3≤2x+2<6\)
Solução
O primeiro método é escrever duas desigualdades separadas:\(3≤2x+2\) e as\(2x+2<6.\) resolvemos de forma independente.
\ [\ begin {array} {lcr}
3≤2x+2 &\ text {e} & 2x+2<6\\ [5pt]
1≤2x & & & 2x<4\\ [5pt]
\ tfrac {1} {2}\ leq x & & x < 2
\ end {array}\ nonumber\]
Então, podemos reescrever a solução como uma desigualdade composta, da mesma forma que o problema começou.
\[\frac{1}{2}≤x<2\nonumber\]
Na notação de intervalo, a solução é escrita como\([\tfrac{1}{2},\, 2).\)
O segundo método é deixar a desigualdade composta intacta e realizar procedimentos de resolução nas três partes ao mesmo tempo.
\ (\ begin {align*}\ qquad 3&≤2x+2<6\\ [5pt]
1&≤2x<4 & &\ text {Isole o termo da variável e subtraia} 2\ text {das três partes.}\\ [5pt]
\ tfrac {1} {2} &≤x<2 & &\ text {Divida as três partes por} 2.
\ end {align*}\)
Nós temos a mesma solução:\([\tfrac{1}{2},\, 2).\)
Resolva a desigualdade composta:\(4<2x−8≤10.\)
- Responda
-
\(6<x≤9\)ou\((6,9]\)
Resolva a desigualdade composta com variáveis em todas as três partes:\(3+x>7x−2>5x−10.\)
Solução
Vamos tentar o primeiro método. Escreva duas desigualdades:
\ [\ begin {array} {ccc} 3+x>7x−2 &\ texto {e} & 7x−2>5x−10\\ [5pt]
3>6x−2 e & 2x−2>−10\\ [5pt]
5>6x e & 2x>−8\\ [5pt]
\ tfrac {5} {6} >x & & -4<x\\ [5 pontos]
\ end {array}\ nonumber\]
O conjunto de soluções é\(−4<𝑥<\tfrac{5}{6}\) ou em notação de intervalo.\(\left(−4,\tfrac{5}{6}\right).\) Observe que quando escrevemos a solução em notação de intervalo, o número menor vem primeiro. Lemos os intervalos da esquerda para a direita, conforme aparecem em uma reta numérica. Veja a Figura\(\PageIndex{3}\).

Resolva a desigualdade composta:\(3y<4−5y<5+3y.\)
- Responda
-
\(\left(−\tfrac{1}{8},\, \tfrac{1}{2}\right)\)
Resolvendo desigualdades de valores absolutos
Como sabemos, o valor absoluto de uma quantidade é um número positivo ou zero. Da origem, um ponto localizado em\((−x,\, 0)\) tem um valor absoluto de,\(x,\) pois está a\(x\) unidades de distância. Considere o valor absoluto como a distância de um ponto a outro ponto. Independentemente da direção, positiva ou negativa, a distância entre os dois pontos é representada como um número positivo ou zero.
Uma desigualdade de valor absoluto é uma equação da forma
\[|A|<B,\quad |A|≤B, \quad |A|>B,\quad \text{or} \quad|A|≥B,\nonumber\]
Onde\(A,\) e às vezes\(B,\) representa uma expressão algébrica dependente de uma variável\(x.\) Resolver a desigualdade significa encontrar o conjunto de todos os\(x\) valores que satisfazem o problema. Normalmente, esse conjunto será um intervalo ou a união de dois intervalos e incluirá uma faixa de valores.
Existem duas abordagens básicas para resolver desigualdades de valor absoluto: gráfica e algébrica. A vantagem da abordagem gráfica é que podemos ler a solução interpretando os gráficos de duas equações. A vantagem da abordagem algébrica é que as soluções são exatas, pois às vezes é difícil ler soluções precisas em um gráfico.
Suponha que queiramos saber todos os retornos possíveis de um investimento se pudermos ganhar alguma quantia de dinheiro entre $200 e $600. Podemos resolver algebricamente o conjunto de valores\(x\) - de forma que a distância entre\(x\) e\(600\) seja menor ou igual a\(200.\) Nós representamos a distância entre\(x\) e\(600\) como\(| x−600 |,\) e, portanto,\(| x−600 |≤200\) ou
\ [\ begin {array} {c} −200≤x−600≤200\\
−200+600≤x−600+600≤200+600\\
400≤x≤800
\ end {array}\ nonumber\]
Isso significa que nossos retornos seriam entre $400 e $800.
Para resolver desigualdades de valor absoluto, assim como com equações de valor absoluto, escrevemos duas desigualdades e as resolvemos de forma independente.
Para uma expressão algébrica\(X\) e\(k>0,\) um valor absoluto, a desigualdade é uma desigualdade da forma
\ [\ begin {align*} | X |&<k\ text {é equivalente a} −K<x<k\\ [4pt]
| X |&>k\ text {é equivalente a} X<−k\ text {ou} x>k\ end {align*}\]
Essas declarações também se aplicam a\(| X |≤k\) e\(| X |≥k.\)
Descreva todos os valores a uma\(x\)\(4\) distância do número\(5.\)
Solução
Queremos que a distância entre\(x\) e\(5\) seja menor ou igual a\(4.\) Podemos desenhar uma reta numérica, como na Figura,\(\PageIndex{4},\) para representar a condição a ser satisfeita.

A distância de\(x\) até\(5\) pode ser representada usando um símbolo de valor absoluto.\(| x−5 |.\) Escreva os valores\(x\) que satisfazem a condição como uma desigualdade de valor absoluto.
\[| x−5 |≤4\nonumber\]
Precisamos escrever duas desigualdades, pois sempre há duas soluções para uma equação de valor absoluto.
\ [\ begin {array} {ccc} x−5≤4 &\ text {e} & x−5≥−4\\ [4pt]
x≤9 e & x≥1
\ end {matriz}\ nonumber\]
Se o conjunto de soluções for\(x≤9\) e\(x≥1,\), então, o conjunto de soluções é um intervalo que inclui todos os números reais entre e incluindo 1 e 9.
Então\(| x−5 |≤4\) é equivalente a\([ 1,9 ]\) em notação de intervalo.
Descreva todos\(x\) os valores a uma\(3\) distância do número\(2.\)
- Responda
-
\(|x−2|≤3\)
Resolver\(|x−1|≤3.\)
Solução
\ (\ quad\ begin {array} {c} |x−1 |≤3\\ [4pt]
−3≤x−1≤3\\ [4pt]
−2≤x≤4\\ [4pt]
[−2,4]
\ end {matriz}\)
Dada a equação,\(y=−\tfrac{1}{2}|4x−5|+3,\) determine os\(x\) valores -para os quais os\(y\) valores -são negativos.
Solução
Estamos tentando determinar\(y<0,\) onde é quando\(−\tfrac{1}{2}|4x−5|+3<0.\) começamos isolando o valor absoluto.
\ [\ begin {align*} −\ tfrac {1} {2} |4x−5|&<−3 & &\ text {Multiplique os dois lados por} —2,\ text {e reverta a desigualdade.}\\ [5pt]
|4x−5|&>6\ end {align*}\]
Em seguida, resolvemos pela igualdade\(|4x−5|=6.\)
\ [\ begin {array} {rcr} 4x−5=6 & & 4x−5=−6\\ [5pt]
4x=11 &\ text {ou} & 4x=−1\\ [5pt]
x=\ tfrac {11} {4} & & x=−\ tfrac {1} {4}
\ end {array}\ nonumber\]
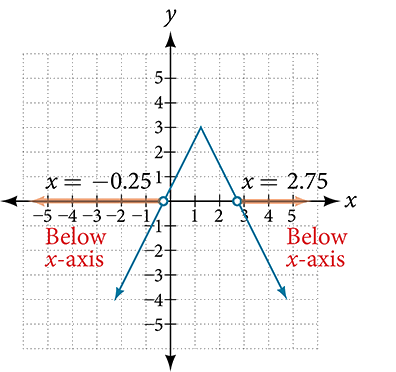
Agora, podemos examinar o gráfico para observar onde os\(y\) valores -são negativos. Observamos onde os galhos estão abaixo\(x\) do eixo. Observe que não é importante exatamente a aparência do gráfico, desde que saibamos que ele cruza o eixo horizontal\(x=−\tfrac{1}{4}\)\(x=\tfrac{11}{4},\) e que o gráfico se abre para baixo. Veja a figura\(\PageIndex{5}.\)
Resolver\(−2|k−4|≤−6.\)
- Responda
-
\(k≤1\)ou\(k≥7;\) na notação de intervalo, isso seria\((−∞,1]∪[7,∞).\)
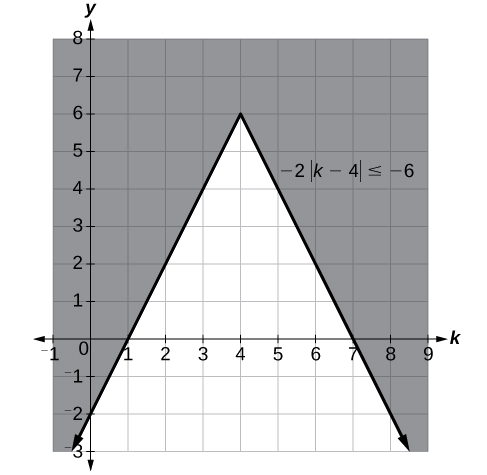
Figura\(\PageIndex{6}\)


