2.7: Outros tipos de equações
- Page ID
- 189275
- Resolva equações envolvendo expoentes racionais.
- Resolva equações usando fatoração.
- Resolva equações radicais.
- Resolva equações de valor absoluto.
- Resolva outros tipos de equações.
Resolvemos equações lineares, equações racionais e equações quadráticas usando vários métodos. No entanto, existem muitos outros tipos de equações e investigaremos mais alguns tipos nesta seção. Examinaremos equações envolvendo expoentes racionais, equações polinomiais, equações radicais, equações de valor absoluto, equações em forma quadrática e algumas equações racionais que podem ser transformadas em quadráticas. Resolver qualquer equação, no entanto, emprega as mesmas regras algébricas básicas. Aprenderemos algumas técnicas novas à medida que elas se aplicam a certas equações, mas a álgebra nunca muda.
Resolvendo equações envolvendo expoentes racionais
Expoentes racionais são expoentes que são frações, onde o numerador é uma potência e o denominador é uma raiz. Por exemplo,\({16}^{\tfrac{1}{2}}\) é outra forma de escrever\(\sqrt{16}\);\(8^{\tfrac{1}{3}}\) é outra forma de escrever\(\sqrt[3]{8}\). A capacidade de trabalhar com expoentes racionais é uma habilidade útil, pois é altamente aplicável no cálculo.
Podemos resolver equações nas quais uma variável é elevada a um expoente racional elevando os dois lados da equação ao inverso do expoente. A razão pela qual elevamos a equação ao inverso do expoente é porque queremos eliminar o expoente no termo variável e um número multiplicado por seu recíproco é igual\(1\). Por exemplo,
\[\dfrac{2}{3}\left (\dfrac{3}{2} \right )=1 \nonumber\]
\[3\left (\dfrac{1}{3} \right )=1, \nonumber\]
e assim por diante.
Um expoente racional indica uma potência no numerador e uma raiz no denominador. Há várias maneiras de escrever uma expressão, uma variável ou um número com um expoente racional:
\[a^{\tfrac{m}{n}}={\left (a^{\tfrac{1}{n}} \right )}^m={a^m}^{\tfrac{1}{n}}=\sqrt[n]{a^m}={(\sqrt[n]{a})}^m\]
Avalie\(8^{\tfrac{2}{3}}\)
Solução
Se pegamos a raiz primeiro ou a potência primeiro, depende do número. É fácil encontrar a raiz cúbica de\(8\), então reescreva\(8^{\tfrac{2}{3}}\) como\({\left (8^{\tfrac{1}{3}} \right )}^2\).
\[\begin{align*} {\left (8^{\tfrac{1}{3}} \right )}^2&= {(2)}^2\\ &= 4 \end{align*}\]
Avalie\({64}^{-\tfrac{1}{3}}\)
- Resposta
-
\(\dfrac{1}{4}\)
Resolva a equação na qual uma variável é elevada a um expoente racional:\(x^{\tfrac{5}{4}} = 32\).
Solução
A maneira de remover o expoente on\(x\) é elevando os dois lados da equação a uma potência que seja o inverso de\(\dfrac{5}{4}\), que é\(\dfrac{4}{5}\).
\[\begin{align*} x^{\tfrac{5}{4}}&= 32\\ {\left(x^{\tfrac{5}{4}}\right)}^{\tfrac{4}{5}}&= {\left(32\right)}^{\tfrac{4}{5}}\\ x&= (2)^4\\ &= 16 \end{align*}\]
Resolva a equação\(x^{\tfrac{3}{2}} = 125\).
- Resposta
-
\(25\)
Resolver\(3x^{\tfrac{3}{4}} = x^{\tfrac{1}{2}}\).
Solução
Essa equação envolve expoentes racionais, bem como a fatoração de expoentes racionais. Vamos dar um passo de cada vez. Primeiro, coloque os termos variáveis em um lado do sinal de igual e defina a equação igual a zero.
\[\begin{align*} 3x^{\tfrac{3}{4}}-\left(x^{\tfrac{1}{2}}\right)&= x^{\tfrac{1}{2}}-\left(x^{\tfrac{1}{2}}\right)\\ 3x^{\tfrac{3}{4}}-x^{\tfrac{1}{2}}&= 0 \end{align*}\]
Agora, parece que devemos considerar o lado esquerdo, mas o que consideramos? Sempre podemos fatorar o termo com o menor expoente. Reescreva\(x^{\tfrac{1}{2}}\) como\(x^{\tfrac{2}{4}}\). Em seguida, considere\(x^{\tfrac{2}{4}}\) os dois termos à esquerda.
\[\begin{align*} 3x^{\tfrac{3}{4}}-x^{\tfrac{1}{2}}&= 0\\ x^{\tfrac{2}{4}}\left (3x^{\tfrac{1}{4}}-1 \right )&= 0 \end{align*}\]
De onde\(x^{\tfrac{1}{4}}\) veio? Lembre-se de que, quando multiplicamos dois números com a mesma base, adicionamos os expoentes. Portanto, se multiplicarmos\(x^{\tfrac{2}{4}}\) novamente usando a propriedade distributiva, obteremos a expressão que tínhamos antes da fatoração, que é o que deveria acontecer. Precisamos de um expoente tal que, quando adicionado a\(\dfrac{2}{4}\) iguais\(\dfrac{3}{4}\). Assim, o\(x\) expoente entre parênteses é\(\dfrac{1}{4}\).
Vamos continuar. Agora temos dois fatores e podemos usar o teorema do fator zero.
\ [\ begin {align*}
x^ {\ tfrac {2} {4}}\ left (3x^ {\ tfrac {1} {4}} -1\ direita) &= 0\\ x^ {\ tfrac {2} {4} &= 0\\
x&= 0\\ 3x^ {\ tfrac {1} {4}}
-1&= 0\\
3x^ {\ tfrac {1} {4}} -1&= 0\\ 3x^ {\ tfrac {1} {4}} -1&= 0\\
3x^ {\ tfrac\
3x^ {\ tfrac {1} {4}} &= 1\\ x^ {\ tfrac {1} {4}} &=\ dfrac {1} {3},\ qquad\ texto {Divida os dois lados por 3.} \\
{\ left (x^ {\ tfrac {1} {4}}\ right)} ^4&= {\ left (\ dfrac {1} {3}\ right)} ^4,\ qquad\ text {Eleve os dois lados até o recíproco de}\ dfrac {1} {4}\\
x&=\ dfrac {1} {81}
\ end {align*}\]
As duas soluções são\(0\)\(\dfrac{1}{81}\) e.
Resolver:\({\left(x+5\right)}^{\tfrac{3}{2}}=8\).
- Resposta
-
\(-1\)
Resolvendo equações usando fatoração
Usamos a fatoração para resolver equações quadráticas, mas é uma técnica que podemos usar com muitos tipos de equações polinomiais, que são equações que contêm uma sequência de termos, incluindo coeficientes numéricos e variáveis. Quando nos deparamos com uma equação contendo polinômios de grau maior que\(2\), muitas vezes podemos resolvê-los por fatoração.
Um polinômio de grau\(n\) é uma expressão do tipo
\[a_nx^n+a_{n−1}x^{n−1}+⋅⋅⋅+a_2x^2+a_1x+a_0\]
onde\(n\) is a positive integer and \(a_n ,…, a_0\) are real numbers and \(a_n≠0\).
Definir o polinômio igual a zero fornece uma equação polinomial. O número total de soluções (reais e complexas) para uma equação polinomial é igual ao maior expoente\(n\).
Resolva o polinômio fatorando:\(5x^4 = 80x^2\).
Solução
Primeiro, defina a equação igual a zero. Em seguida, considere o que é comum a ambos os termos, o GCF.
\[\begin{align*} 5x^4-80x^2&= 0\\ 5x^2(x^2-16)&= 0 \end{align*}\]
Observe que temos a diferença dos quadrados no fator\(x^2−16\), que continuaremos fatorando e obtendo duas soluções. O primeiro termo,\(5x^2\), gera, tecnicamente, duas soluções como o expoente\(2\), mas elas são a mesma solução.
\[\begin{align*} 5x^2&= 0\\ x&=0\\ x^2-16&= 0\\ (x+4)(x-4)&= 0\\ x&= 4\\ x&= -4 \end{align*}\]
As soluções são\(0\) (solução dupla)\(4\),\(−4\) e.
Análise
Podemos ver as soluções no gráfico na Figura\(\PageIndex{1}\). As coordenadas x dos pontos em que o gráfico cruza o\(x\) eixo -são as soluções—as\(x\) interceptações. Observe no gráfico que, na solução\(0\), o gráfico toca o\(x\) eixo -e volta para trás. Ele não cruza o\(x\) eixo y. Isso é típico de soluções duplas.
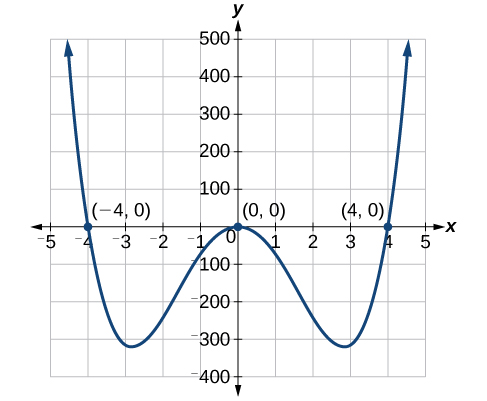
Resolva fatorando:\(12x^4 = 3x^2\).
- Resposta
-
\(x=0, x=12, x=−12\)
Resolva um polinômio agrupando:\(x^3+x^2−9x−9=0\).
Solução
Esse polinômio consiste em\(4\) termos, que podemos resolver agrupando. Os procedimentos de agrupamento exigem fatorar os dois primeiros termos e, em seguida, fatorar os dois últimos termos. Se os fatores entre parênteses forem idênticos, podemos continuar o processo e resolver, a menos que mais fatoração seja sugerida.
\[\begin{align*} x^3+x^2-9x-9&= 0\\ x^2(x+1)-9(x+1)&= 0\\ (x^2-9)(x+1)&= 0 \end{align*}\]
O processo de agrupamento termina aqui, pois podemos fatorar\(x^2−9\) usando a fórmula da diferença dos quadrados.
\[\begin{align*} (x^2-9)(x+1)&= 0\\ (x-3)(x+3)(x+1)&= 0\\ x&= 3\\ x&= -3\\ x&= -1 \end{align*}\]
As soluções são\(3\)\(−3\),\(−1\) e. Observe que o maior expoente é\(3\) e obtivemos\(3\) soluções. Podemos ver as soluções, os interceptos x, no gráfico da Figura\(\PageIndex{2}\).
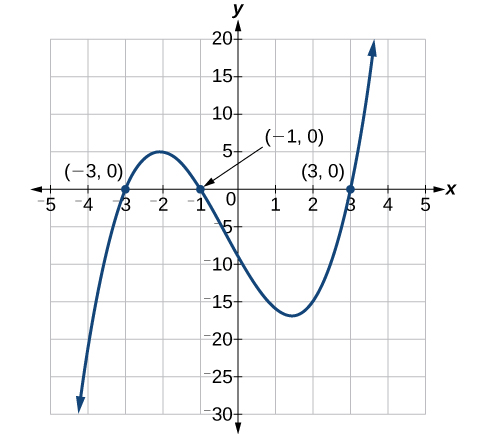
Análise
Analisamos a resolução de equações quadráticas fatorando quando o coeficiente principal é\(1\). Quando o coeficiente principal não é\(1\), resolvemos por agrupamento. O agrupamento requer quatro termos, que obtivemos dividindo o termo linear das equações quadráticas. Também podemos usar o agrupamento para alguns polinômios de grau maior do que\(2\), como vimos aqui, já que já havia quatro termos.
Resolvendo equações radicais
Equações radicais são equações que contêm variáveis no radicando (a expressão sob um símbolo radical), como
\[\sqrt{3x+18}=x \nonumber\]
\[\sqrt{x+3}=x-3 \nonumber\]
\[\sqrt{x+5}-\sqrt{x-3}=2 \nonumber\]
As equações radicais podem ter um ou mais termos radicais e são resolvidas eliminando cada radical, um de cada vez. Devemos ter cuidado ao resolver equações radicais, pois não é incomum encontrar soluções estranhas, raízes que não são, de fato, soluções para a equação. Essas soluções não se devem a um erro no método de resolução, mas resultam do processo de elevar os dois lados de uma equação a uma potência. No entanto, verificar cada resposta na equação original confirmará as soluções verdadeiras.
Uma equação contendo termos com uma variável no radicando é chamada de equação radical.
- Isole a expressão radical em um lado do sinal de igual. Coloque todos os termos restantes do outro lado.
- Se o radical for uma raiz quadrada, então eleve ao quadrado os dois lados da equação. Se for uma raiz cúbica, eleve os dois lados da equação até a terceira potência. Em outras palavras, para um radical\(n^{th}\) raiz, eleve os dois lados ao\(n^{th}\) poder. Fazer isso elimina o símbolo radical.
- Resolva a equação restante.
- Se um termo radical ainda persistir, repita as etapas 1—2.
- Confirme as soluções substituindo-as na equação original.
Resolver\(\sqrt{15−2x}=x\).
Solução
O radical já está isolado no lado esquerdo do lado igual, então passe para o quadrado dos dois lados.
\[\begin{align*} \sqrt{15-2x}&= x\\ {\left (\sqrt{15-2x} \right )}^2&= {(x)}^2\\ 15-2x&= x^2 \end{align*}\]
Vemos que a equação restante é quadrática. Defina-o como igual a zero e resolva.
\[\begin{align*} 0&= x^2+2x-15\\ 0&= (x+5)(x-3)\\ x&= -5\\ x&= 3 \end{align*}\]
As soluções propostas são\(−5\)\(3\) e. Vamos verificar cada solução na equação original. Primeiro, verifique\(x=−5\).
\[\begin{align*} \sqrt{15-2x}&= x\\ \sqrt{15-2(-5)}&=-5\\ \sqrt{25}&= -5\\ 5&\neq -5 \end{align*}\]
Essa é uma solução estranha. Embora nenhum erro tenha sido cometido ao resolver a equação, encontramos uma solução que não satisfaz a equação original.
Confira\(x=3\).
\[\begin{align*} \sqrt{15-2x}&= x\\ \sqrt{15-2(3)}&= 3\\ \sqrt{9}&= 3\\ 3&= 3 \end{align*}\]
A solução é\(3\).
Resolva a equação radical:\(\sqrt{x+3}=3x-1\)
- Resposta
-
\(x=1\), solução estranha\(x=−\dfrac{2}{9}\)
Resolver\(\sqrt{2x+3}+\sqrt{x-2}=4\)
Solução
Como essa equação contém dois radicais, isolamos um radical, o eliminamos e depois isolamos o segundo radical.
\[\sqrt{2x+3}+\sqrt{x-2}=4 \nonumber\]
\[\begin{align*} \sqrt{2x+3}&= 4-\sqrt{x-2} \qquad \text{Subtract } \sqrt{x-2} \text{ from both sides}\\ {\left (\sqrt{2x+3} \right )}^2&= {\left (4-\sqrt{x-2} \right )}^2\qquad \text{Square both sides} \end{align*}\]
Use a fórmula quadrada perfeita para expandir o lado direito:\({(a−b)}^2=a^2−2ab+b^2\).
\[\begin{align*} 2x+3&= {(4)}^2-2(4)\sqrt{x-2}+{(\sqrt{x-2})}^2\\ 2x+3&= 16-8\sqrt{x-2}+(x-2)\\ 2x+3&= 14+x-8\sqrt{x-2} \qquad \text{Combine like terms}\\ x-11&= -8\sqrt{x-2} \qquad \text{Isolate the second radical}\\ {(x-11)}^2&= {(-8\sqrt{x-2})}^2 \qquad \text{Square both sides}\\ x^2-22x+121&= 64(x-2) \end{align*}\]
Agora que os dois radicais foram eliminados, defina a quadrática como igual a zero e resolva.
\[\begin{align*} x^2-22x+121&= 64x-128\\ x^2-86x+249&= 0\\ (x-3)(x-83)&= 0\\ x&= 3\\ x&= 83 \end{align*}\]
As soluções propostas são\(3\)\(83\) e. Verifique cada solução na equação original.
\[\begin{align*} \sqrt{2x+3}+\sqrt{x-2}&= 4\\ \sqrt{2x+3}&= 4-\sqrt{x-2}\\ \sqrt{2(3)+3}&= 4-\sqrt{(3)-2}\\ \sqrt{9}&= 4-\sqrt{1}\\ 3&= 3 \end{align*}\]
Uma solução é\(3\).
Confira\(x=83\).
\[\begin{align*} \sqrt{2x+3}+\sqrt{x-2}&= 4\\ \sqrt{2x+3}&= 4-\sqrt{x-2}\\ \sqrt{2(83)+3}&= 4-\sqrt{(83)-2}\\ \sqrt{169}&= 4-\sqrt{81}\\ 13&\neq -5 \end{align*}\]
A única solução é\(3\). Vemos que\(x=83\) é uma solução estranha.
Resolva a equação com dois radicais:\(\sqrt{3x+7}+\sqrt{x+2}=1\)
- Resposta
-
\(x=−2\), solução estranha\(x=−1\)
Resolvendo uma equação de valor absoluto
A seguir, aprenderemos como resolver uma equação de valor absoluto. Para resolver uma equação como\(|2x−6|=8\), notamos que o valor absoluto será igual a\(8\) se a quantidade dentro das barras de valor absoluto for\(8\) ou\(−8\). Isso leva a duas equações diferentes que podemos resolver de forma independente.
\[\begin{align*} 2x-6&= 8\\ 2x&= 14\\ x&= 7 \end{align*}\]
OU
\[\begin{align*} 2x-6&= -8\\ 2x&= -2\\ x&= -1 \end{align*}\]
Saber como resolver problemas envolvendo funções de valor absoluto é útil. Por exemplo, talvez precisemos identificar números ou pontos em uma linha que estão a uma distância especificada de um determinado ponto de referência.
O valor absoluto de\(x\) é escrito como\(|x|\). Tem as seguintes propriedades:
Se\(x≥0\), então\(|x|=x\) .If\(x<0\), então\(x=−x\).
Para números reais\(A\) e\(B\), uma equação da forma\(|A|=B\), com\(B≥0\), terá soluções quando\(A=B\) ou\(A=−B\). Se\(B<0\), a equação não\(|A|=B\) tem solução.
Uma equação de valor absoluto no formulário\(|ax+b|=c\) tem as seguintes propriedades:
- Se\(c<0\), não\(|ax+b|=c\) tem solução.
- Se\(c=0\),\(|ax+b|=c\) tem uma solução.
- Se\(c>0\),\(|ax+b|=c\) tem duas soluções.
Dada uma equação de valor absoluto, resolva-a.
- Isole a expressão do valor absoluto em um lado do sinal de igual.
- Se\(c>0\), escreva e resolva duas equações:\(ax+b=c\)\(ax+b=−c\) e.
Resolva as seguintes equações de valor absoluto:
- \(|6x+4|=8\)
- \(|3x+4|=−9\)
- \(|3x−5|−4=6\)
- \(|−5x+10|=0\)
Solução
- \(|6x+4|=8\)
Escreva duas equações e resolva cada uma:
\[\begin{align*} 6x+4&= 8\\ 6x&= 4\\ x&= \dfrac{2}{3} \end{align*}\]
OU
\[\begin{align*} 6x+4&= -8\\ 6x&= -12\\ x&= -2 \end{align*}\]
As duas soluções são\(\dfrac{2}{3}\)\(−2\) e.
- \(|3x+4|=−9\)
Não há solução, pois um valor absoluto não pode ser negativo.
- \(|3x−5|−4=6\)
Isole a expressão do valor absoluto e, em seguida, escreva duas equações.
\[\begin{align*} |3x-5|-4&= 6\\ |3x-5|&= 10\\ 3x-5&= 10\\ 3x&= 15\\ x&= 5 \end{align*}\]
OU
\[\begin{align*} 3x-5&= -10\\ 3x=-5\\ x=\dfrac{5}{3} \end{align*}\]
Há duas soluções:\(5\),\(-\dfrac{5}{3}\) e.
- \(|−5x+10|=0\)
A equação é definida como igual a zero, então temos que escrever apenas uma equação.
\[\begin{align*} -5x+10&= 0\\ -5x&= -10\\ x&= 2 \end{align*}\]
Existe uma solução:\ (2\).
Resolva a equação do valor absoluto:\(|1−4x|+8=13\).
- Resposta
-
\(x=−1, x=\dfrac{3}{2}\)
Resolvendo outros tipos de equações
Existem muitos outros tipos de equações além das que discutimos até agora. Veremos mais delas ao longo do texto. Aqui, discutiremos equações que estão na forma quadrática e equações racionais que resultam em uma quadrática.
Resolvendo equações em forma quadrática
Equações na forma quadrática são equações com três termos. O primeiro termo tem um poder diferente de\(2\). O termo intermediário tem um expoente que é metade do expoente do termo principal. O terceiro termo é uma constante. Podemos resolver equações dessa forma como se fossem quadráticas. Alguns exemplos dessas equações incluem\(x^4−5x^2+4=0\)\(x^6+7x^3−8=0\),\(x^{\tfrac{2}{3}} +4x^{\tfrac{1}{3}}+2=0\) e. Em cada um, dobrar o expoente do termo médio é igual ao expoente do termo principal. Podemos resolver essas equações substituindo uma variável pelo termo médio.
Se o expoente no termo médio for metade do expoente no termo principal, temos uma equação na forma quadrática, que podemos resolver como se fosse quadrática. Substituímos uma variável pelo termo médio para resolver equações na forma quadrática.
- Identifique o expoente no termo principal e determine se ele é o dobro do expoente no termo médio.
- Se estiver, substitua uma variável, como\(u\), pela parte variável do termo intermediário.
- Reescreva a equação para que ela assuma a forma padrão de uma quadrática.
- Resolva usando um dos métodos usuais para resolver uma quadrática.
- Substitua a variável de substituição pelo termo original.
- Resolva a equação restante.
Resolva esta equação de quarto grau:\(3x^4−2x^2−1=0\).
Solução
Essa equação se encaixa no critério principal, de que a potência no termo principal é o dobro da potência no médio prazo. Em seguida, faremos uma substituição para o termo variável no meio. Deixe\(u =x^2\). Reescreva a equação em\(u\).
\[3u^2−2u−1=0 \nonumber\]
Agora resolva a quadrática.
\[\begin{align*} 3u^2-2u-1&= 0\\ (3u+1)(u-1)&= 0 \end{align*}\]
Resolva cada fator e substitua o termo original por\(u\).
\[\begin{align*} 3u+1&= 0\\ 3u&= -1\\ u&= -\dfrac{1}{3}\\ x^2&= -\dfrac{1}{3}\\ x&= \pm i\sqrt{\dfrac{1}{3}}\\ u-1&= 0\\ u&= 1\\ x^2&= 1\\ x&= \pm 1 \end{align*}\]
As soluções são\(x=±i\sqrt{\dfrac{1}{3}}\) e\(x=±1\)
Resolva usando a substituição:\(x^4−8x^2−9=0\).
- Resposta
-
\(x=−3,3,−i,i\)
Resolva a equação na forma quadrática:\({(x+2)}^2+11(x+2)−12=0\).
Solução
Essa equação contém um binômio no lugar da variável única. A tendência é expandir o que é apresentado. No entanto, reconhecer que ele se encaixa nos critérios para estar na forma quadrática faz toda a diferença no processo de resolução. Primeiro, faça uma substituição, deixando\(u =x+2\). Em seguida, reescreva a equação em\(u\).
\[\begin{align*} u^2+11u-12&= 0\\ (u+12)(u-1)&= 0 \end{align*}\]
Resolva usando a propriedade de fator zero e, em seguida,\(u\) substitua pela expressão original.
\[\begin{align*} u+12&= 0\\ u&= -12\\ x+2&= -12\\ x&= -14 \end{align*}\]
O segundo fator resulta em
\[\begin{align*} u-1&= 0\\ u&= 1\\ x+2&= 1\\ x&= -1 \end{align*}\]
Temos duas soluções:\(−14\),\(−1\) e.
Resolver:\({(x−5)}^2−4(x−5)−21=0\).
- Resposta
-
\(x=2,x=12\)
Resolvendo equações racionais que resultam em uma quadrática
Anteriormente, resolvemos equações racionais. Às vezes, resolver uma equação racional resulta em uma equação quadrática. Quando isso acontece, continuamos a solução simplificando a equação quadrática por um dos métodos que vimos. Pode acontecer que não haja solução.
Resolva a seguinte equação racional:\(\dfrac{-4x}{x-1}+\dfrac{4}{x+1}=\dfrac{-8}{x^2-1}\)
Solução
Queremos que todos os denominadores em formato fatorado encontrem o LCD. Dois dos denominadores não podem ser mais considerados. No entanto,\(x^2−1=(x+1)(x−1)\). Então, o LCD é\((x+1)(x−1)\). Em seguida, multiplicamos toda a equação pelo LCD.
\ [\ begin {align*} (x+1) (x-1)\ esquerda (\ dfrac {-4x} {x-1} +\ dfrac {4} {x+1}\ direita) &=\ esquerda (\ dfrac {-8} {x^2-1}\ direita) (x+1) (x-1)\ -4x (x+1) +4 (x-1) &= -8\\ -4x^2-4x+4x-4&= -8\\ -4x^2+4&= 0\\
-4 (x^2-1) &= 0\\ -4 (x+1) (x-1) &= 0\\ x&= -1\\ x&= 1\ end {alinhamento*}\]
Nesse caso, qualquer solução produz um zero no denominador na equação original. Portanto, não há solução.
Resolver\(\dfrac{3x+2}{x-2}+\dfrac{1}{x}=\dfrac{-2}{x^2-2x}\)
- Resposta
-
\(x=−1, x= 0\)não é uma solução.
Acesse esses recursos on-line para obter instruções e práticas adicionais com diferentes tipos de equações.
- Equação racional sem solução
- Resolução de equações com expoentes racionais usando potências recíprocas
- Resolvendo equações radicais, parte 1 de 2
- Resolvendo equações radicais, parte 2 de 2
Conceitos chave
- Os expoentes racionais podem ser reescritos de várias maneiras, dependendo do que for mais conveniente para o problema. Para resolver, ambos os lados da equação são elevados a uma potência que tornará o expoente da variável igual\(1\) a. Veja exemplo, exemplo e exemplo.
- A fatoração se estende a polinômios de ordem superior quando envolve fatorar o GCF ou fatorar por agrupamento. Veja o exemplo e o exemplo.
- Podemos resolver equações radicais isolando o radical e elevando os dois lados da equação a uma potência que corresponda ao índice. Veja o exemplo e o exemplo.
- Para resolver equações de valor absoluto, precisamos escrever duas equações, uma para o valor positivo e outra para o valor negativo. Veja o exemplo.
- As equações na forma quadrática são fáceis de identificar, pois o expoente no primeiro termo é o dobro do expoente no segundo termo e o terceiro termo é uma constante. Também podemos ver um binômio no lugar da variável única. Usamos a substituição para resolver. Veja o exemplo e o exemplo.
- Resolver uma equação racional também pode levar a uma equação quadrática ou a uma equação na forma quadrática. Veja o exemplo.


