3.3: Desenvolvimento da Teoria Quântica
- Page ID
- 195508
- Estenda o conceito de dualidade onda-partícula que foi observado na radiação eletromagnética para a matéria também
- Entenda a ideia geral da descrição mecânica quântica de elétrons em um átomo e que ela usa a noção de funções de onda tridimensionais, ou orbitais, que definem a distribuição de probabilidade para encontrar um elétron em uma parte específica do espaço
- Liste e descreva as características dos quatro números quânticos que formam a base para especificar completamente o estado de um elétron em um átomo
O modelo de Bohr explicou os dados experimentais do átomo de hidrogênio e foi amplamente aceito, mas também levantou muitas questões. Por que os elétrons orbitam apenas a distâncias fixas definidas por um único número quântico n = 1, 2, 3 e assim por diante, mas nunca entre elas? Por que o modelo funcionou tão bem descrevendo íons de hidrogênio e de um elétron, mas não conseguiu prever corretamente o espectro de emissão de hélio ou qualquer átomo maior? Para responder a essas perguntas, os cientistas precisaram revisar completamente a maneira como pensavam sobre a matéria.
Comportamento no mundo microscópico
Sabemos como a matéria se comporta no mundo macroscópico — objetos grandes o suficiente para serem vistos a olho nu seguem as regras da física clássica. Uma bola de bilhar que se move sobre uma mesa se comportará como uma partícula: ela continuará em linha reta, a menos que colida com outra bola ou com a almofada da mesa, ou seja acionada por alguma outra força (como atrito). A bola tem uma posição e velocidade bem definidas (ou um momento bem definido\(p = mv\), definido pela massa\(m\) e velocidade\(v\)) em qualquer momento. Em outras palavras, a bola está se movendo em uma trajetória clássica. Esse é o comportamento típico de um objeto clássico.
Quando as ondas interagem umas com as outras, elas mostram padrões de interferência que não são exibidos por partículas macroscópicas, como a bola de bilhar. Por exemplo, ondas interativas na superfície da água podem produzir padrões de interferência semelhantes aos mostrados na Figura\(\PageIndex{1}\). Este é um caso de comportamento das ondas na escala macroscópica, e está claro que partículas e ondas são fenômenos muito diferentes no reino macroscópico.

Como as melhorias tecnológicas permitiram aos cientistas sondar o mundo microscópico com mais detalhes, ficou cada vez mais claro na década de 1920 que pedaços muito pequenos de matéria seguem um conjunto de regras diferente daquelas que observamos para objetos grandes. A separação inquestionável de ondas e partículas não era mais o caso do mundo microscópico.
Uma das primeiras pessoas a prestar atenção ao comportamento especial do mundo microscópico foi Louis de Broglie. Ele fez a pergunta: Se a radiação eletromagnética pode ter um caráter semelhante a uma partícula, os elétrons e outras partículas submicroscópicas podem exibir um caráter ondulatório? Em sua tese de doutorado de 1925, de Broglie ampliou a dualidade onda-partícula da luz que Einstein usou para resolver o paradoxo do efeito fotoelétrico em partículas de material. Ele previu que uma partícula com massa m e velocidade v (ou seja, com momento linear p) também deveria exibir o comportamento de uma onda com um valor de comprimento de onda λ, dado por essa expressão na qual h é a constante de Planck familiar
\[\lambda=\dfrac{h}{mv}=\dfrac{h}{p} \label{6.4.1} \]
Isso é chamado de comprimento de onda de Broglie. Ao contrário dos outros valores de λ discutidos neste capítulo, o comprimento de onda de Broglie é uma característica de partículas e outros corpos, não de radiação eletromagnética (observe que essa equação envolve velocidade [v, m/s], não frequência [¾, Hz]. Embora esses dois símbolos sejam idênticos, eles significam coisas muito diferentes). Onde Bohr postulou o elétron como sendo uma partícula orbitando o núcleo em órbitas quantizadas, de Broglie argumentou que a suposição de quantização de Bohr pode ser explicada se o elétron for considerado não como uma partícula, mas sim como uma onda estacionária circular, de modo que apenas um número inteiro de comprimentos de onda poderia caber exatamente dentro da órbita (Figura\(\PageIndex{2}\)).
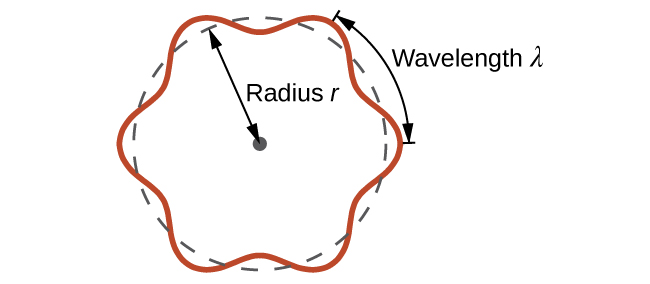
Para uma órbita circular de raio r, a circunferência é 2π r e, portanto, a condição de Broglie é:
\[2πr=nλ \label{6.4.3} \]
com\(n=1,2,3,...\)
Como a expressão de Broglie relaciona o comprimento de onda com o momento e, portanto, com a velocidade, isso implica:
\[2πr=nλ=\dfrac{nh}{p}=\dfrac{nh}{mv}=\dfrac{nhr}{mvr}=\dfrac{nhr}{L} \label{6.4.3b} \]
Essa expressão pode ser reorganizada para fornecer a fórmula de Bohr para a quantização do momento angular:
\[L=\dfrac{nh}{2π}=n \hbar \label{6.4.4} \]
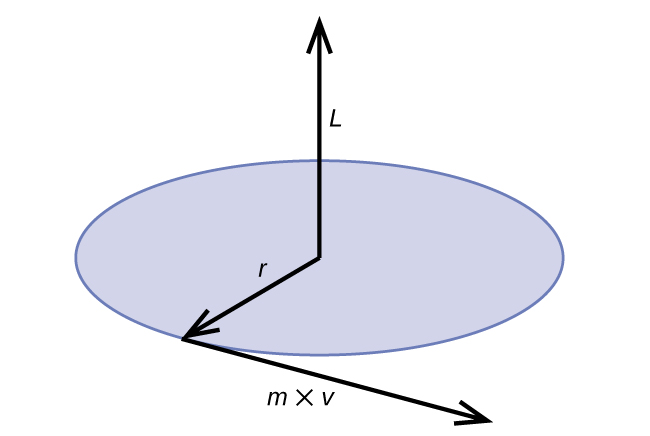
O momento angular clássico L para um movimento circular é igual ao produto do raio do círculo e do momento da partícula em movimento p.
\[L=rp=rmv \;\;\; \text{(for a circular motion)} \label{6.4.5} \]
Pouco depois de de Broglie propor a natureza ondulatória da matéria, dois cientistas dos Laboratórios Bell, C. J. Davisson e L. H. Germer, demonstraram experimentalmente que os elétrons podem exibir um comportamento ondulatório ao mostrar um padrão de interferência para elétrons que viajam através de um padrão atômico em um cristal. As camadas atômicas regularmente espaçadas serviram como fendas, conforme usadas em outros experimentos de interferência. Como o espaçamento entre as camadas que servem como fendas precisa ser semelhante em tamanho ao comprimento de onda da onda testada para que um padrão de interferência se forme, Davisson e Germer usaram um alvo de níquel cristalino para suas “fendas”, uma vez que o espaçamento dos átomos dentro da rede era aproximadamente o mesmo que o Comprimentos de onda de Broglie dos elétrons que eles usaram. A figura\(\PageIndex{4}\) mostra um padrão de interferência.
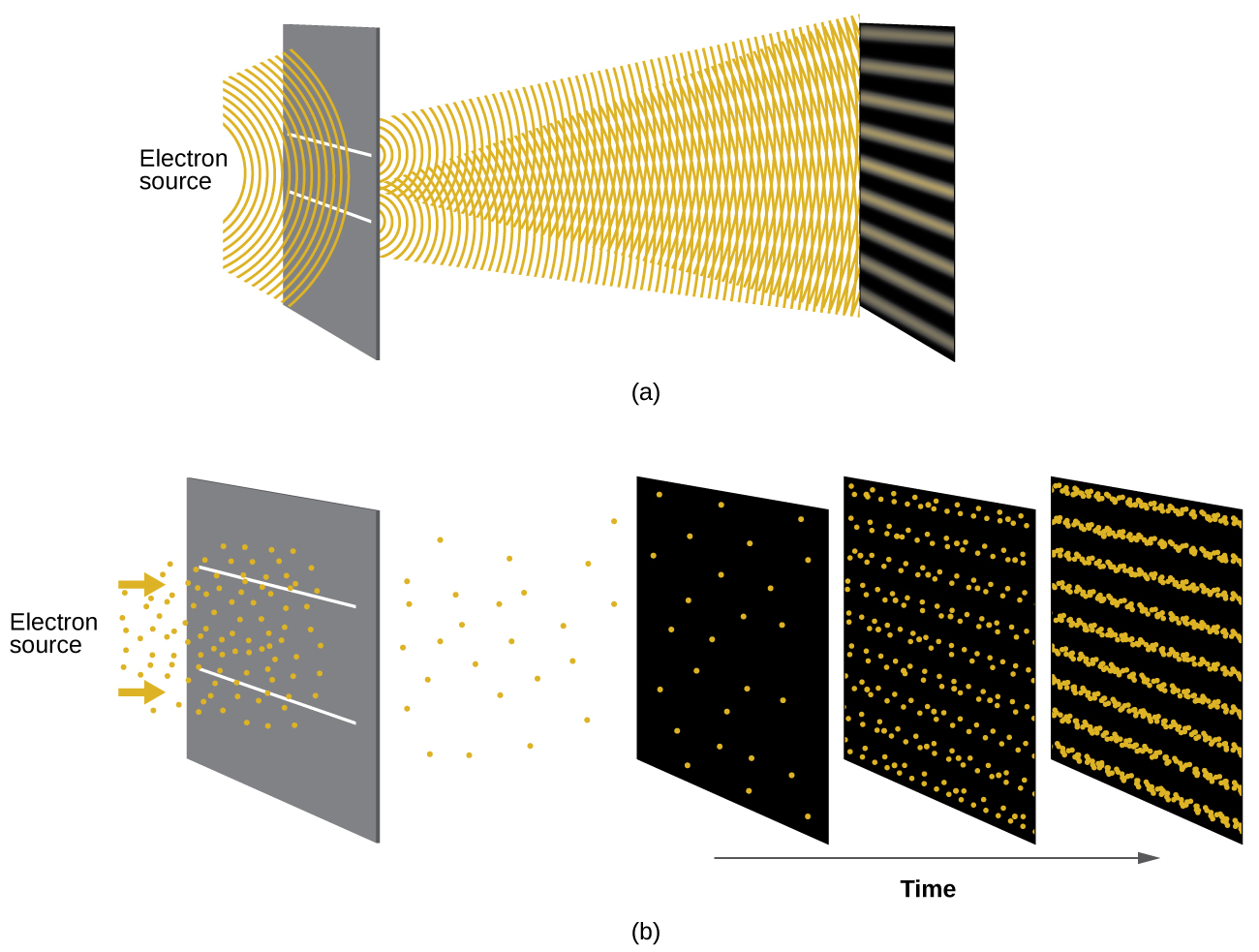
A dualidade onda-partícula da matéria pode ser vista observando o que acontece se as colisões de elétrons forem registradas por um longo período de tempo. Inicialmente, quando apenas alguns elétrons foram registrados, eles mostram um comportamento claro de partículas, tendo chegado em pequenos pacotes localizados que parecem aleatórios. À medida que mais e mais elétrons chegavam e eram registrados, surgiu um claro padrão de interferência que é a marca registrada do comportamento ondulatório. Assim, parece que, embora os elétrons sejam pequenas partículas localizadas, seu movimento não segue as equações de movimento implícitas na mecânica clássica, mas é governado por algum tipo de equação de onda que governa uma distribuição de probabilidade mesmo para o movimento de um único elétron. Assim, a dualidade onda-partícula observada pela primeira vez com fótons é, na verdade, um comportamento fundamental intrínseco a todas as partículas quânticas.
Se um elétron viaja a uma velocidade de 1.000 × 10 7 m s —1 e tem uma massa de 9,109 × 10 —28 g, qual é seu comprimento de onda?
Solução
Podemos usar a equação de Broglie para resolver esse problema, mas primeiro precisamos fazer uma conversão unitária da constante de Planck. Você aprendeu anteriormente que 1 J = 1 kg m 2 /s 2. Assim, podemos escrever h = 6,626 × 10 —34 J s como 6,626 × 10 —34 kg m 2 /s.
\[\begin{align*} λ&=\dfrac{h}{mv} \\[4pt] &=\mathrm{\dfrac{6.626×10^{−34}\:kg\: m^2/s}{(9.109×10^{−31}\:kg)(1.000×10^7\:m/s)}}\\[4pt] &= \mathrm{7.274×10^{−11}\:m} \end{align*} \nonumber \]
Esse é um valor pequeno, mas é significativamente maior do que o tamanho de um elétron na visão clássica (partícula). Esse tamanho é da mesma ordem de magnitude do tamanho de um átomo. Isso significa que o comportamento semelhante à onda do elétron será perceptível em um átomo.
Calcule o comprimento de onda de uma bola de softball com uma massa de 100 g viajando a uma velocidade de 35 m s —1, assumindo que ela possa ser modelada como uma única partícula.
- Responda
-
1,9 × 10 —34 m.
Nunca pensamos em uma bola de softball lançada com um comprimento de onda, já que esse comprimento de onda é tão pequeno que é impossível que nossos sentidos ou qualquer instrumento conhecido detectem (estritamente falando) o comprimento de onda de uma bola de beisebol real corresponderia aos comprimentos de onda de seus átomos e moléculas constituintes, que, embora muito maiores do que esse valor, ainda seria microscopicamente pequeno). O comprimento de onda de Broglie só é apreciável para matéria que tem uma massa muito pequena e/ou uma velocidade muito alta.
Werner Heisenberg considerou os limites da precisão com que podemos medir as propriedades de um elétron ou de outras partículas microscópicas. Ele determinou que há um limite fundamental para a precisão com que se pode medir a posição e o momento de uma partícula simultaneamente. Quanto mais precisos medirmos o momento de uma partícula, menos precisos podemos determinar sua posição naquele momento e vice-versa. Isso se resume no que agora chamamos de princípio da incerteza de Heisenberg: é fundamentalmente impossível determinar simultaneamente e exatamente o momento e a posição de uma partícula. Para uma partícula de massa m se movendo com velocidade v x na direção x (ou equivalentemente com momento p x), o produto da incerteza na posição, Δx, e a incerteza no momento, Δp x, deve ser maior ou igual a\(\dfrac{ℏ}{2}\) (lembre-se disso\(ℏ=\dfrac{h}{2π}\), o valor da constante de Planck dividido por 2 π).
\[Δx×Δp_x=(Δx)(mΔv)≥\dfrac{ℏ}{2} \nonumber \]
Essa equação nos permite calcular o limite da precisão com que podemos saber a posição simultânea de um objeto e seu momento. Por exemplo, se melhorarmos nossa medição da posição de um elétron para que a incerteza na posição (Δx) tenha um valor de, digamos, 1 pm (10 —12 m, cerca de 1% do diâmetro de um átomo de hidrogênio), então nossa determinação de seu momento deve ter uma incerteza com um valor de pelo menos
\[\left [Δp=mΔv=\dfrac{h}{(2Δx)} \right ]=\mathrm{\dfrac{(1.055×10^{−34}\:kg\: m^2/s)}{(2×1×10^{−12}\:m)}=5×10^{−23}\:kg\: m/s.} \nonumber \]
O valor de não é grande, então a incerteza na posição ou no momento de um objeto macroscópico como uma bola de beisebol é muito insignificante para ser observada. No entanto, a massa de um objeto microscópico, como um elétron, é pequena o suficiente para que a incerteza possa ser grande e significativa.
Deve-se notar que o princípio da incerteza de Heisenberg não se limita apenas às incertezas de posição e momentum, mas também vincula outras variáveis dinâmicas. Por exemplo, quando um átomo absorve um fóton e faz a transição de um estado de energia para outro, a incerteza na energia e a incerteza no tempo necessário para a transição estão similarmente relacionadas, como ΔE Δt ≥\(\dfrac{ℏ}{2}\). Como será discutido mais adiante, nem mesmo os componentes vetoriais do momento angular podem ser especificados exatamente simultaneamente.
O princípio de Heisenberg impõe limites máximos sobre o que é conhecido na ciência. Pode-se demonstrar que o princípio da incerteza é uma consequência da dualidade onda-partícula, que está no cerne do que distingue a teoria quântica moderna da mecânica clássica. Lembre-se de que as equações de movimento obtidas da mecânica clássica são trajetórias em que, a qualquer instante no tempo, tanto a posição quanto o momento de uma partícula podem ser determinados com exatidão. O princípio da incerteza de Heisenberg implica que tal visão é insustentável no domínio microscópico e que existem limitações fundamentais que governam o movimento das partículas quânticas. Isso não significa que as partículas microscópicas não se movam em trajetórias, apenas que as medições das trajetórias são limitadas em sua precisão. No campo da mecânica quântica, as medições introduzem mudanças no sistema que está sendo observado.
O modelo quântico-mecânico de um átomo
Pouco depois de de Broglie publicar suas ideias de que o elétron em um átomo de hidrogênio poderia ser melhor considerado como uma onda estacionária circular em vez de uma partícula se movendo em órbitas circulares quantizadas, como Bohr argumentou, Erwin Schrödinger ampliou o trabalho de de Broglie incorporando a relação de Broglie em um equação de onda, derivando o que hoje é conhecido como equação de Schrödinger. Quando Schrödinger aplicou sua equação a átomos semelhantes a hidrogênio, ele foi capaz de reproduzir a expressão de Bohr para a energia e, portanto, a fórmula de Rydberg que governava os espectros de hidrogênio, e ele fez isso sem ter que invocar as suposições de Bohr sobre estados estacionários e órbitas quantizadas, momentos angulares e energias; a quantização na teoria de Schrödinger foi uma consequência natural da matemática subjacente da equação da onda. Como de Broglie, Schrödinger inicialmente via o elétron no hidrogênio como sendo uma onda física em vez de uma partícula, mas onde de Broglie pensava no elétron em termos de ondas estacionárias circulares, Schrödinger pensava adequadamente em termos de ondas estacionárias tridimensionais, ou funções de onda, representado pela letra grega psi,. Alguns anos depois, Max Born propôs uma interpretação da função de onda que ainda é aceita hoje: os elétrons ainda são partículas e, portanto, as ondas representadas por não são ondas físicas, mas, em vez disso, são amplitudes de probabilidade complexas. O quadrado da magnitude de uma função de onda\(∣ψ∣^2\) descreve a probabilidade da partícula quântica estar presente perto de um determinado local no espaço. Isso significa que as funções de onda podem ser usadas para determinar a distribuição da densidade do elétron em relação ao núcleo em um átomo. Na forma mais geral, a equação de Schrödinger pode ser escrita como:
\[\hat{H}ψ=Eψ \nonumber \]
\(\hat{H}\)é o operador hamiltoniano, um conjunto de operações matemáticas que representam a energia total da partícula quântica (como um elétron em um átomo), é a função de onda dessa partícula que pode ser usada para encontrar a distribuição especial da probabilidade de encontrar a partícula, e \(E\)é o valor real da energia total da partícula.
O trabalho de Schrödinger, assim como o de Heisenberg e muitos outros cientistas seguindo seus passos, é geralmente chamado de mecânica quântica.
Entendendo a teoria quântica de elétrons em átomos
O objetivo desta seção é entender os orbitais de elétrons (localização dos elétrons nos átomos), suas diferentes energias e outras propriedades. O uso da teoria quântica fornece a melhor compreensão desses tópicos. Esse conhecimento é um precursor da ligação química.
Conforme descrito anteriormente, os elétrons nos átomos só podem existir em níveis discretos de energia, mas não entre eles. Diz-se que a energia de um elétron em um átomo é quantizada, ou seja, pode ser igual apenas a certos valores específicos e pode pular de um nível de energia para outro, mas não transitar suavemente ou permanecer entre esses níveis.
Os níveis de energia são rotulados com um valor n, onde n = 1, 2, 3,... De um modo geral, a energia de um elétron em um átomo é maior para valores maiores de n. Esse número, n, é conhecido como o número quântico principal. O número quântico principal define a localização do nível de energia. É essencialmente o mesmo conceito do n na descrição do átomo de Bohr. Outro nome para o número quântico principal é o número da casca. As camadas de um átomo podem ser pensadas em círculos concêntricos irradiando para fora do núcleo. Os elétrons que pertencem a uma camada específica têm maior probabilidade de serem encontrados na área circular correspondente. Quanto mais nos afastamos do núcleo, maior o número de conchas e, portanto, maior o nível de energia (Figura\(\PageIndex{5}\)). Os prótons carregados positivamente no núcleo estabilizam os orbitais eletrônicos por atração eletrostática entre as cargas positivas dos prótons e as cargas negativas dos elétrons. Portanto, quanto mais distante o elétron estiver do núcleo, maior será a energia que ele tem.
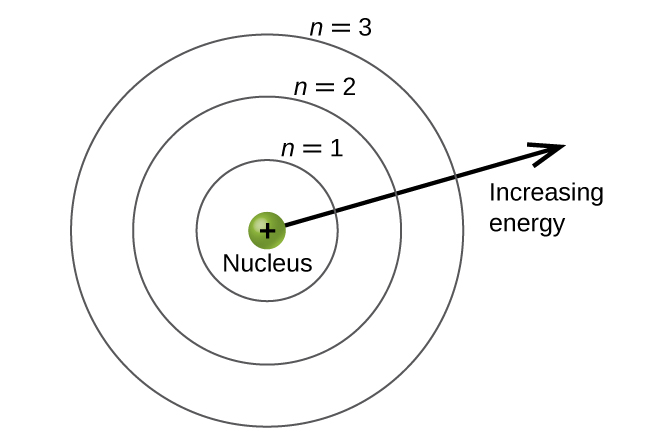
Esse modelo de mecânica quântica para onde os elétrons residem em um átomo pode ser usado para observar as transições eletrônicas, os eventos em que um elétron se move de um nível de energia para outro. Se a transição for para um nível de energia mais alto, a energia será absorvida e a mudança de energia terá um valor positivo. Para obter a quantidade de energia necessária para a transição para um nível de energia mais alto, um fóton é absorvido pelo átomo. A transição para um nível de energia mais baixo envolve uma liberação de energia e a mudança de energia é negativa. Esse processo é acompanhado pela emissão de um fóton pelo átomo. A equação a seguir resume essas relações e é baseada no átomo de hidrogênio:
\[ \begin{align*} ΔE &=E_\ce{final}−E_\ce{initial} \\[4pt] &=−2.18×10^{−18}\left(\dfrac{1}{n^2_\ce f}−\dfrac{1}{n^2_\ce i}\right)\:\ce J \end{align*} \nonumber \]
Os valores n f e n i são os estados de energia final e inicial do elétron.
O número quântico principal é um dos três números quânticos usados para caracterizar um orbital. Um orbital atômico, que é distinto de uma órbita, é uma região geral em um átomo na qual é mais provável que um elétron resida. O modelo de mecânica quântica especifica a probabilidade de encontrar um elétron no espaço tridimensional ao redor do núcleo e é baseado em soluções da equação de Schrödinger. Além disso, o número quântico principal define a energia de um elétron em um átomo ou íon semelhante a hidrogênio ou hidrogênio (um átomo ou íon com apenas um elétron) e a região geral na qual os níveis discretos de energia dos elétrons em átomos e íons de vários elétrons estão localizados.
Outro número quântico é l, o número quântico do momento angular. É um número inteiro que define a forma do orbital e assume os valores, l = 0, 1, 2,..., n — 1. Isso significa que um orbital com n = 1 pode ter apenas um valor de l, l = 0, enquanto n = 2 permite l = 0 e l = 1, e assim por diante. O número quântico principal define o tamanho geral e a energia do orbital. O valor l especifica a forma do orbital. Orbitais com o mesmo valor de l formam uma subcamada. Além disso, quanto maior o número quântico do momento angular, maior é o momento angular de um elétron nesse orbital.
Orbitais com l = 0 são chamados de orbitais s (ou subcamadas s). O valor l = 1 corresponde aos orbitais p. Para um dado n, os orbitais p constituem uma subcamada p (por exemplo, 3 p se n = 3). Os orbitais com l = 2 são chamados de orbitais d, seguidos pelos orbitais f-, g- e h- para l = 3, 4, 5, e há valores mais altos que não consideraremos.
Existem certas distâncias do núcleo nas quais a densidade de probabilidade de encontrar um elétron localizado em um orbital específico é zero. Em outras palavras, o valor da função de onda λ é zero nessa distância para esse orbital. Esse valor de raio r é chamado de nó radial. O número de nós radiais em um orbital é n — l — 1.
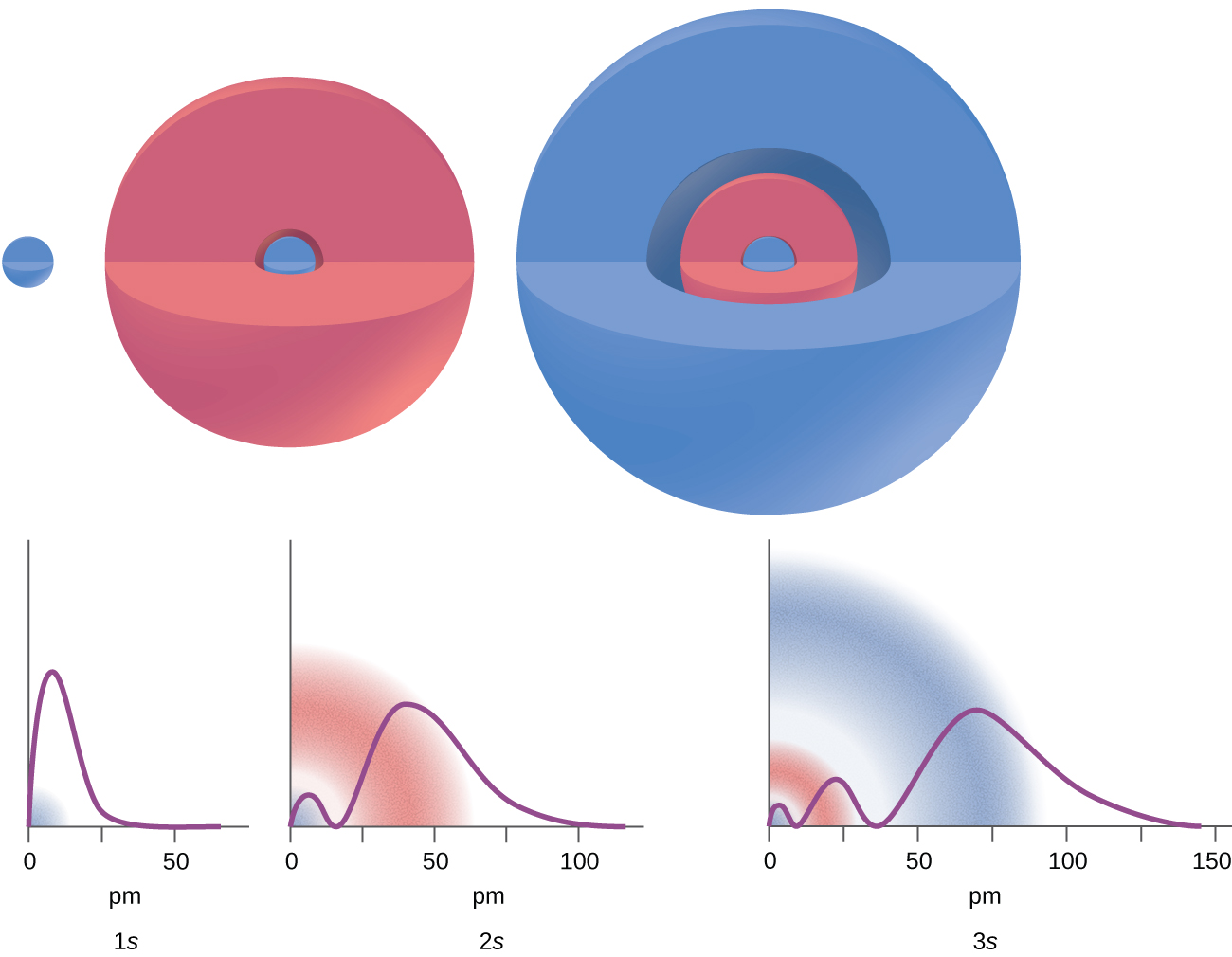
Considere os exemplos na Figura\(\PageIndex{7}\). Os orbitais representados são do tipo s, portanto l = 0 para todos eles. Pode ser visto nos gráficos das densidades de probabilidade que existem 1 — 0 — 1 = 0 lugares onde a densidade é zero (nós) para 1 s (n = 1), 2 — 0 — 1 = 1 nó por 2 s e 3 — 0 — 1 = 2 nós para os orbitais de 3 s.
A distribuição da densidade eletrônica da subcamada s é esférica e a subcamada p tem uma forma de haltere. Os orbitais d e f são mais complexos. Essas formas representam as regiões tridimensionais nas quais o elétron provavelmente será encontrado.
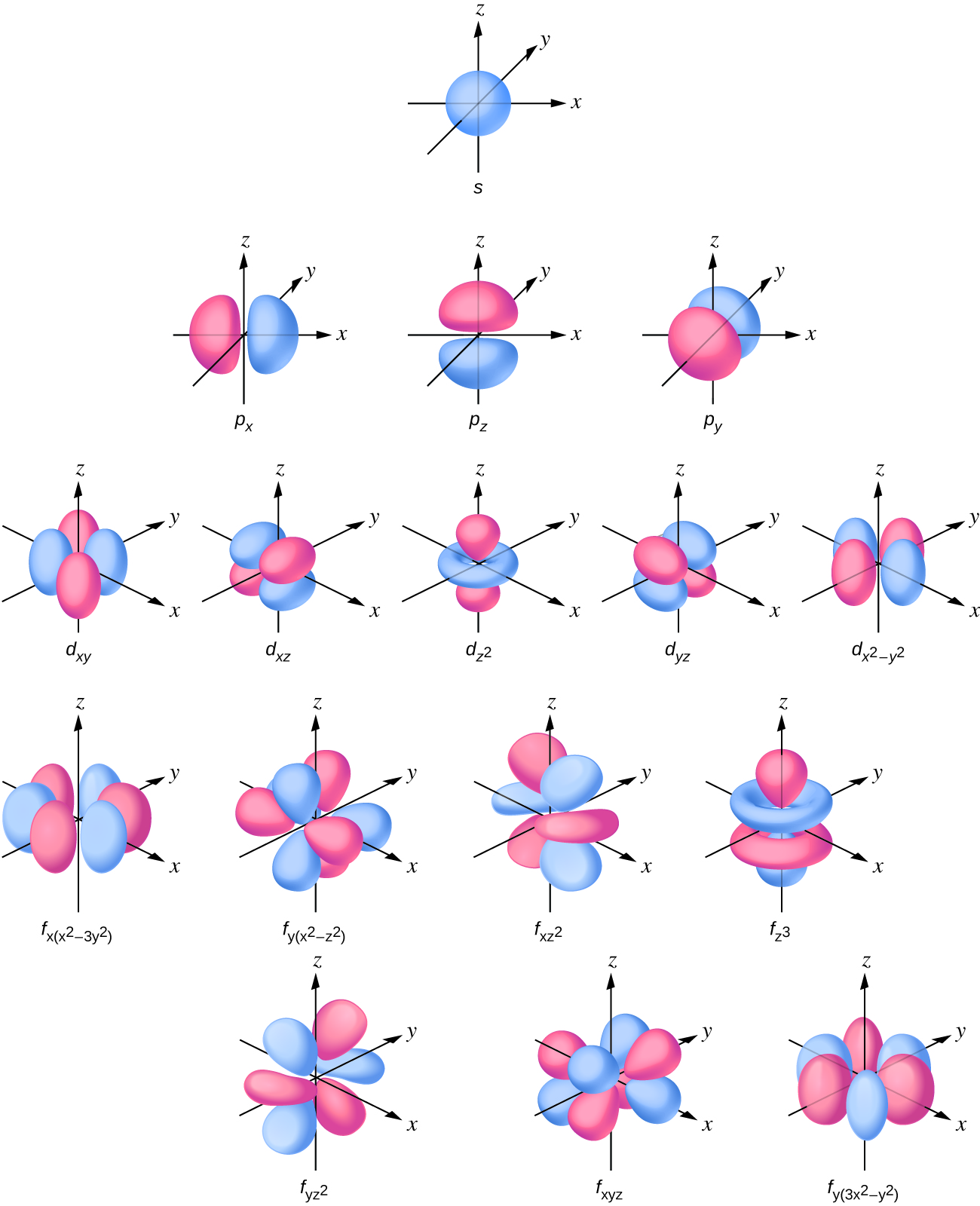
Se um elétron tem um momento angular (l ≠ 0), esse vetor pode apontar em direções diferentes. Além disso, o componente z do momento angular pode ter mais de um valor. Isso significa que se um campo magnético for aplicado na direção z, orbitais com valores diferentes do componente z do momento angular terão energias diferentes resultantes da interação com o campo. O número quântico magnético, chamado m l, especifica o componente z do momento angular para um orbital específico. Por exemplo, para um orbital s, l = 0, e o único valor de m l é zero. Para orbitais p, l = 1 e m l podem ser iguais a —1, 0 ou +1. De um modo geral, m l pode ser igual a — l, — (l — 1),..., —1, 0, +1,..., (l — 1), l. O número total de orbitais possíveis com o mesmo valor de l (uma subcamada) é 2 l + 1. Assim, há um orbital s para ml = 0, há três orbitais p para ml = 1, cinco orbitais d para ml = 2, sete orbitais f para ml = 3 e assim por diante. O número quântico principal define o valor geral da energia eletrônica. O número quântico do momento angular determina a forma do orbital. E o número quântico magnético especifica a orientação do orbital no espaço, como pode ser visto na Figura\(\PageIndex{7}\).
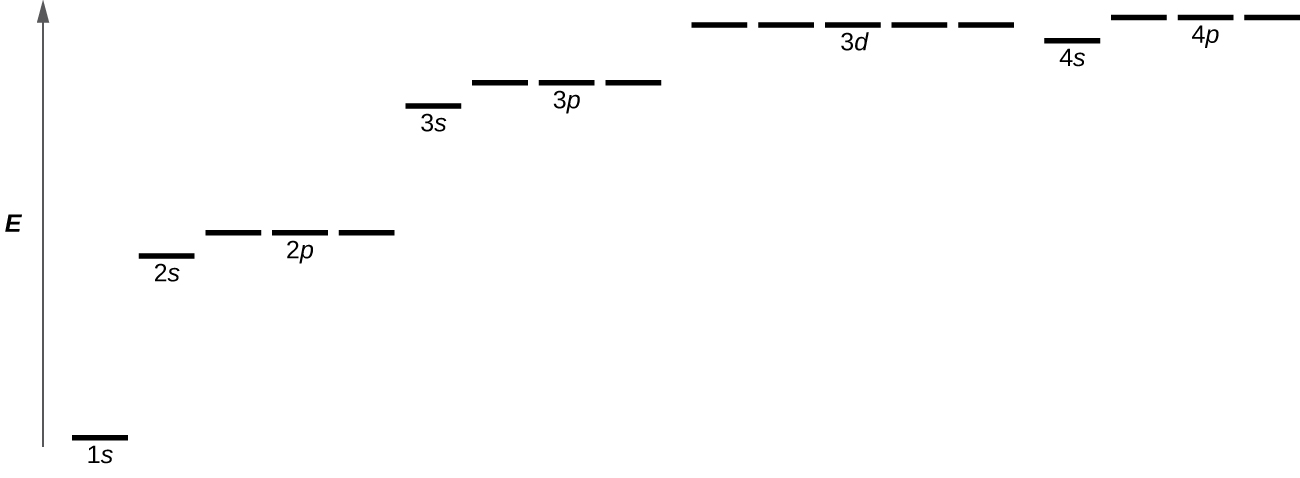
A figura\(\PageIndex{8}\) ilustra os níveis de energia de vários orbitais. O número antes do nome orbital (como 2 s, 3 p e assim por diante) representa o número quântico principal, n. A letra no nome orbital define a subcamada com um número quântico de momento angular específico l = 0 para orbitais s, 1 para orbitais p, 2 para orbitais d. Finalmente, há mais de um orbital possível para l ≥ 1, cada um correspondendo a um valor específico de m l. No caso de um átomo de hidrogênio ou de um íon de um elétron (como He +, Li 2 + e assim por diante), as energias de todos os orbitais com o mesmo n são as mesmas. Isso é chamado de degeneração, e os níveis de energia para o mesmo número quântico principal, n, são chamados de níveis de energia degenerados. No entanto, em átomos com mais de um elétron, essa degeneração é eliminada pelas interações elétron-elétron, e orbitais que pertencem a diferentes subcamadas têm energias diferentes. Orbitais dentro da mesma subcamada (por exemplo ns, np, nd, nf, como 2 p, 3 s) ainda são degenerados e têm a mesma energia.
Embora os três números quânticos discutidos nos parágrafos anteriores funcionem bem para descrever orbitais de elétrons, alguns experimentos mostraram que eles não eram suficientes para explicar todos os resultados observados. Foi demonstrado na década de 1920 que, quando os espectros de linhas de hidrogênio são examinados em resolução extremamente alta, algumas linhas na verdade não são picos únicos, mas sim pares de linhas estreitamente espaçadas. Essa é a chamada estrutura fina do espectro e implica que existem pequenas diferenças adicionais nas energias dos elétrons, mesmo quando eles estão localizados no mesmo orbital. Essas observações levaram Samuel Goudsmit e George Uhlenbeck a propor que os elétrons têm um quarto número quântico. Eles chamaram isso de número quântico de spin, ou m s.
Os outros três números quânticos, n, l e m l, são propriedades de orbitais atômicos específicos que também definem em qual parte do espaço um elétron tem maior probabilidade de estar localizado. Os orbitais são o resultado da resolução da equação de Schrödinger para elétrons em átomos. O spin do elétron é um tipo diferente de propriedade. É um fenômeno completamente quântico sem análogos no reino clássico. Além disso, ela não pode ser derivada da resolução da equação de Schrödinger e não está relacionada às coordenadas espaciais normais (como os cartesianos x, y e z). O spin eletrônico descreve uma “rotação” ou “rotação” intrínseca de elétrons. Cada elétron atua como um pequeno ímã ou um pequeno objeto rotativo com um momento angular, mesmo que essa rotação não possa ser observada em termos de coordenadas espaciais.
A magnitude do spin geral do elétron só pode ter um valor, e um elétron só pode “girar” em um dos dois estados quantizados. Um é denominado estado α, com o componente z do spin na direção positiva do eixo z. Isso corresponde ao número quântico de spin\(m_s=\dfrac{1}{2}\). O outro é chamado de estado β, com o componente z do spin sendo negativo\(m_s=−\dfrac{1}{2}\) e. Qualquer elétron, independentemente do orbital atômico em que está localizado, só pode ter um desses dois valores do número quântico de spin. As energias dos elétrons têm\(m_s=−\dfrac{1}{2}\) e\(m_s=\dfrac{1}{2}\) são diferentes se um campo magnético externo for aplicado.
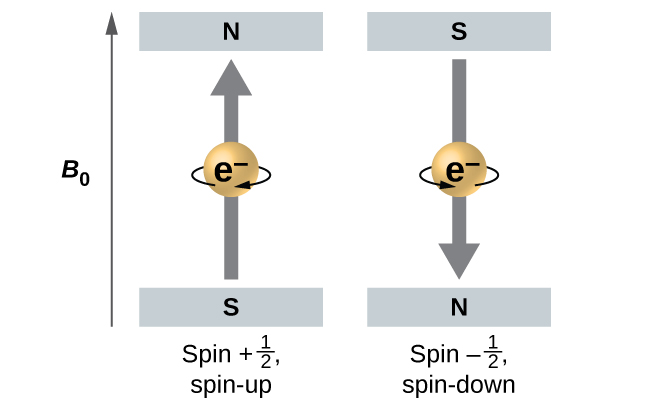
A figura\(\PageIndex{9}\) ilustra esse fenômeno. Um elétron age como um pequeno ímã. Seu momento é direcionado para cima (na direção positiva do eixo z) para o número quântico de\(\dfrac{1}{2}\) spin e para baixo (na direção z negativa) para o número quântico de spin de\(−\ce{1/2}\). Um ímã tem uma energia menor se seu momento magnético estiver alinhado com o campo magnético externo (o elétron esquerdo) e uma energia maior para o momento magnético sendo oposta ao campo aplicado. É por isso que um elétron com\(m_s=\dfrac{1}{2}\) tem uma energia ligeiramente menor em um campo externo na direção z positiva e um elétron com\(m_s=−\dfrac{1}{2}\) uma energia um pouco maior no mesmo campo. Isso é verdade até mesmo para um elétron ocupando o mesmo orbital em um átomo. Uma linha espectral correspondente a uma transição para elétrons do mesmo orbital, mas com números quânticos de spin diferentes, tem dois valores possíveis de energia; portanto, a linha no espectro mostrará uma divisão fina da estrutura.
O princípio de exclusão de Pauli
Um elétron em um átomo é completamente descrito por quatro números quânticos: n, l, m l e m s. Os primeiros três números quânticos definem o orbital e o quarto número quântico descreve a propriedade intrínseca do elétron chamada spin. O físico austríaco Wolfgang Pauli formulou um princípio geral que fornece a última informação de que precisamos para entender o comportamento geral dos elétrons nos átomos. O princípio de exclusão de Pauli pode ser formulado da seguinte forma: Dois elétrons no mesmo átomo não podem ter exatamente o mesmo conjunto de todos os quatro números quânticos. O que isso significa é que os elétrons podem compartilhar o mesmo orbital (o mesmo conjunto dos números quânticos n, l e m l), mas somente se seus números quânticos de spin m s tiverem valores diferentes. Como o número quântico de spin só pode ter dois valores\(\left(±\dfrac{1}{2}\right)\), não mais do que dois elétrons podem ocupar o mesmo orbital (e se dois elétrons estiverem localizados no mesmo orbital, eles devem ter spins opostos). Portanto, qualquer orbital atômico pode ser preenchido por apenas zero, um ou dois elétrons. As propriedades e o significado dos números quânticos de elétrons nos átomos estão resumidos brevemente na Tabela\(\PageIndex{1}\).
| Nome | Símbolo | Valores permitidos | Significado físico |
|---|---|---|---|
| número quântico principal | n | 1, 2, 3, 4,... | concha, a região geral do valor da energia de um elétron no orbital |
| momento angular ou número quântico azimutal | l | 0 ≤ l ≤ n — 1 | subconcha, a forma do orbital |
| número quântico magnético | m l | — l ≤ m l ≤ l | orientação do orbital |
| número quântico de spin | m é | \(\dfrac{1}{2},\:−\dfrac{1}{2}\) | direção da “rotação” quântica intrínseca do elétron |
Indique o número de subcamadas, o número de orbitais em cada subcamada e os valores de l e m l para os orbitais na camada n = 4 de um átomo.
Solução
Para n = 4, l pode ter valores de 0, 1, 2 e 3. Assim, as subcamadas s, p, d e f são encontradas na camada n = 4 de um átomo. Para l = 0 (a subcamada s), m l só pode ser 0. Assim, há apenas um orbital de 4 s. Para l = 1 (orbitais do tipo p), m pode ter valores de —1, 0, +1, então encontramos três orbitais de 4 p. Para l = 2 (orbitais do tipo d), m l pode ter valores de —2, —1, 0, +1, +2, então temos cinco orbitais de 4 d. Quando l = 3 (orbitais do tipo f), m l pode ter valores de —3, —2, —1, 0, +1, +2, +3, e podemos ter sete orbitais 4f. Assim, encontramos um total de 16 orbitais na camada n = 4 de um átomo.
Identifique a subcamada na qual os elétrons com os seguintes números quânticos são encontrados:
- n = 3, l = 1;
- n = 5, l = 3;
- n = 2, l = 0.
- Responda a
-
3 págs
- Resposta b
-
5 g
- Resposta c
-
2s
Calcule o número máximo de elétrons que podem ocupar uma camada com (a) n = 2, (b) n = 5 e (c) n como variável. Observe que você está observando apenas os orbitais com o valor n especificado, não aqueles com energias mais baixas.
Solução
(a) Quando n = 2, existem quatro orbitais (um único orbital de 2 s e três orbitais marcados com 2 p). Esses quatro orbitais podem conter oito elétrons.
(b) Quando n = 5, há cinco subcamadas de orbitais que precisamos somar:
&\ phantom {+}\ textrm {1 orbital rotulado} 5s\\
&\ phantom {+}\ textrm {3 orbitais rotulados} 5p\\
&\ phantom {+}\ textrm {5 orbitais rotulados} 5d\\
&\ phantom {+}\ textrm {7 orbitais rotulados como} bitais rotulados como} 5f\\
&\ underline {+\ textrm {9 orbitais rotulados como} 5g}\\
&\,\ textrm {25 orbitais no total}
\ end {align*}\)
Novamente, cada orbital contém dois elétrons, então 50 elétrons podem caber nessa camada.
(c) O número de orbitais em qualquer concha n será igual a n 2. Pode haver até dois elétrons em cada orbital, então o número máximo de elétrons será 2 × n 2
Se uma camada contém no máximo 32 elétrons, qual é o número quântico principal, n?
- Responda
-
n = 4
Preencha a tabela a seguir para orbitais atômicos:
| Orbital | n | l | m l degeneração | Nódulos radiais (não.) |
|---|---|---|---|---|
| 4 g | ||||
| 4 | 1 | |||
| 7 | 7 | 3 | ||
| 5 d |
Solução
A tabela pode ser preenchida usando as seguintes regras:
- A designação orbital é nl, onde l = 0, 1, 2, 3, 4, 5,... é mapeada na sequência de letras s, p, d, f, g, h,...,
- A degeneração m l é o número de orbitais dentro de uma subcamada l, assim como 2 l + 1 (há um orbital s, três orbitais p, cinco orbitais d, sete orbitais f e assim por diante).
- O número de nós radiais é igual a n — l — 1.
| Orbital | n | l | m l degeneração | Nódulos radiais (não.) |
|---|---|---|---|---|
| 4 g | 4 | 3 | 7 | 0 |
| 4 p | 4 | 1 | 3 | 2 |
| 7 de | 7 | 3 | 7 | 3 |
| 5 d | 5 | 2 | 5 | 2 |
Quantos orbitais têm l = 2 e n = 3?
- Responda
-
Os cinco orbitais degenerados de 3 d
Resumo
Objetos macroscópicos agem como partículas. Objetos microscópicos (como elétrons) têm propriedades tanto de uma partícula quanto de uma onda. Suas trajetórias exatas não podem ser determinadas. O modelo de mecânica quântica dos átomos descreve a posição tridimensional do elétron de forma probabilística de acordo com uma função matemática chamada função de onda, frequentemente denotada como. As funções de onda atômica também são chamadas de orbitais. A magnitude quadrada da função de onda descreve a distribuição da probabilidade de encontrar o elétron em uma determinada região no espaço. Portanto, os orbitais atômicos descrevem as áreas em um átomo onde os elétrons têm maior probabilidade de serem encontrados.
Um orbital atômico é caracterizado por três números quânticos. O número quântico principal, n, pode ser qualquer número inteiro positivo. A região geral do valor da energia do orbital e a distância média de um elétron do núcleo estão relacionadas a n. Diz-se que orbitais com o mesmo valor de n estão na mesma concha. O número quântico do momento angular, l, pode ter qualquer valor inteiro de 0 a n — 1. Esse número quântico descreve a forma ou o tipo do orbital. Orbitais com o mesmo número quântico principal e o mesmo valor l pertencem à mesma subcamada. O número quântico magnético, m l, com 2 l + 1 valores variando de — l a + l, descreve a orientação do orbital no espaço. Além disso, cada elétron tem um número quântico de spin, m s, que pode ser igual\(±\dfrac{1}{2}\) a. Dois elétrons no mesmo átomo não podem ter o mesmo conjunto de valores para todos os quatro números quânticos.
Glossário
- número quântico de momento angular (l)
- número quântico que distingue as diferentes formas dos orbitais; também é uma medida do momento angular orbital
- orbital atômico
- função matemática que descreve o comportamento de um elétron em um átomo (também chamada de função de onda), ela pode ser usada para encontrar a probabilidade de localizar um elétron em uma região específica ao redor do núcleo, bem como outras variáveis dinâmicas
- d orbital
- região do espaço com alta densidade eletrônica que é de quatro lóbulos ou contém um haltere e forma de toróide; descreve orbitais com l = 2. Um elétron neste orbital é chamado de elétron d
- densidade de elétrons
- uma medida da probabilidade de localizar um elétron em uma determinada região do espaço, é igual ao valor absoluto quadrado da função de onda
- f orbital
- região multilobada do espaço com alta densidade eletrônica, descreve orbitais com l = 3. Um elétron neste orbital é chamado de elétron f
- Princípio da incerteza Heisenberg
- regra que afirma que é impossível determinar com exatidão certas propriedades dinâmicas conjugadas, como o momento e a posição de uma partícula ao mesmo tempo. O princípio da incerteza é uma consequência de partículas quânticas exibirem dualidade onda-partícula
- número quântico magnético (m l)
- número quântico que significa a orientação de um orbital atômico ao redor do núcleo; orbitais com valores diferentes de m l, mas o mesmo valor de subcamada de l, têm a mesma energia (são degenerados), mas essa degeneração pode ser removida pela aplicação de um magnético externo campo
- p orbital
- região do espaço em forma de haltere com alta densidade eletrônica, descreve orbitais com l = 1. Um elétron neste orbital é chamado de elétron p
- princípio de exclusão de Pauli
- especifica que dois elétrons em um átomo não podem ter o mesmo valor para todos os quatro números quânticos
- número quântico principal (n)
- número quântico especificando a camada que um elétron ocupa em um átomo
- mecânica quântica
- campo de estudo que inclui quantização de energia, dualidade onda-partícula e o princípio da incerteza de Heisenberg para descrever a matéria
- é orbital
- região esférica do espaço com alta densidade eletrônica, descreve orbitais com l = 0. Um elétron neste orbital é chamado de elétron s.
- concha
- conjunto de orbitais com o mesmo número quântico principal, n
- número quântico de spin (m s)
- número especificando a direção de rotação do elétron,\(+\dfrac{1}{2}\) ou\(−\dfrac{1}{2}\)
- subconcha
- conjunto de orbitais em um átomo com os mesmos valores de n e l
- função de onda ()
- descrição matemática de um orbital atômico que descreve a forma do orbital; ele pode ser usado para calcular a probabilidade de encontrar o elétron em qualquer local no orbital, bem como variáveis dinâmicas, como a energia e o momento angular


