3.2: O modelo de Bohr

Last updated
Save as PDF

Page ID: 195493

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Descreva o modelo de Bohr do átomo de hidrogênio
Use a equação de Rydberg para calcular as energias da luz emitida ou absorvida pelos átomos de hidrogênio

Seguindo o trabalho de Ernest Rutherford e seus colegas no início do século XX, a imagem de átomos consistindo em pequenos núcleos densos cercados por elétrons mais leves e ainda menores se movendo continuamente ao redor do núcleo estava bem estabelecida. Essa imagem foi chamada de modelo planetário, pois retratava o átomo como um “sistema solar” em miniatura com os elétrons orbitando o núcleo como planetas orbitando o sol. O átomo mais simples é o hidrogênio, consistindo de um único próton como núcleo sobre o qual um único elétron se move. A força eletrostática que atrai o elétron para o próton depende apenas da distância entre as duas partículas.

\[ F_{gravity} = G \dfrac{ m_1 m_2}{r^2} \nonumber \]

com

\(G\)é uma constante gravitacional
\(m_1\)e\(m_2\) são as massas da partícula 1 e 2, respectivamente
\(r\)é a distância entre as duas partículas

A força eletrostática tem a mesma forma que a força gravitacional entre duas partículas de massa, exceto que a força eletrostática depende das magnitudes das cargas nas partículas (+1 para o próton e −1 para o elétron) em vez das magnitudes das massas de partículas que governam a gravitacional força.

\[ F_{electrostatic} = k \dfrac{ m_1 m_2}{r^2} \nonumber \]

com

\(k\)é uma constante
\(m_1\)e\(m_2\) são as massas da partícula 1 e 2, respectivamente
\(r\)é a distância entre as duas partículas

Como as forças podem ser derivadas de potenciais, é conveniente trabalhar com potenciais, pois são formas de energia. O potencial eletrostático também é chamado de potencial de Coulomb. Como o potencial eletrostático tem a mesma forma do potencial gravitacional, de acordo com a mecânica clássica, as equações de movimento devem ser semelhantes, com o elétron se movendo ao redor do núcleo em órbitas circulares ou elípticas (daí o rótulo modelo “planetário” do átomo). Potenciais da forma V (r) que dependem somente da distância radial\(r\) são conhecidos como potenciais centrais. Os potenciais centrais têm simetria esférica e, portanto, em vez de especificar a posição do elétron nas coordenadas cartesianas usuais (x, y, z), é mais conveniente usar coordenadas esféricas polares centradas no núcleo, consistindo em uma coordenada linear r e duas coordenadas angulares, geralmente especificadas pelas letras gregas teta (θ) e phi (Φ). Essas coordenadas são semelhantes às usadas em dispositivos GPS e na maioria dos smartphones que rastreiam posições em nossa Terra (quase) esférica, com as duas coordenadas angulares especificadas pela latitude e longitude e a coordenada linear especificada pela elevação do nível do mar. Por causa da simetria esférica dos potenciais centrais, a energia e o momento angular do átomo de hidrogênio clássico são constantes, e as órbitas são limitadas a ficar em um plano como os planetas que orbitam o sol. Essa descrição mecânica clássica do átomo está incompleta, no entanto, uma vez que um elétron se movendo em uma órbita elíptica estaria acelerando (mudando de direção) e, de acordo com o eletromagnetismo clássico, deveria emitir continuamente radiação eletromagnética. Essa perda de energia orbital deve fazer com que a órbita do elétron fique cada vez menor até entrar em espiral no núcleo, o que implica que os átomos são inerentemente instáveis.

Em 1913, Niels Bohr tentou resolver o paradoxo atômico ignorando a previsão do eletromagnetismo clássico de que o elétron em órbita no hidrogênio emitiria luz continuamente. Em vez disso, ele incorporou à mecânica clássica a descrição do átomo das ideias de quantização de Planck e a descoberta de Einstein de que a luz consiste em fótons cuja energia é proporcional à sua frequência. Bohr presumiu que o elétron orbitando o núcleo normalmente não emitiria nenhuma radiação (a hipótese do estado estacionário), mas emitiria ou absorveria um fóton se fosse movido para uma órbita diferente. A energia absorvida ou emitida refletiria diferenças nas energias orbitais de acordo com esta equação:

\[ |ΔE|=|E_f−E_i|=h u=\dfrac{hc}{\lambda} \label{6.3.1} \]

Nessa equação, h é a constante de Planck e E _i e E _f são as energias orbitais inicial e final, respectivamente. O valor absoluto da diferença de energia é usado, pois as frequências e os comprimentos de onda são sempre positivos. Em vez de permitir valores contínuos para o momento angular, a energia e o raio da órbita, Bohr assumiu que apenas valores discretos para eles poderiam ocorrer (na verdade, quantificar qualquer um deles implicaria que os outros dois também são quantizados). A expressão de Bohr para as energias quantizadas é:

\[E_n=−\dfrac{k}{n^2} \label{6.3.2} \]

com\(n=1,2,3, ...\)

Nesta expressão,\(k\) é uma constante que compreende constantes fundamentais, como a massa e a carga do elétron e a constante de Planck. Inserindo a expressão para as energias da órbita na equação de\(ΔE\) dá

\[ \color{red} ΔE=k \left(\dfrac{1}{n^2_1}−\dfrac{1}{n_2^2}\right)=\dfrac{hc}{\lambda} \label{6.3.3} \]

\[ \dfrac{1}{\lambda}=\dfrac{k}{hc} \left(\dfrac{1}{n^2_1}−\dfrac{1}{n_2^2}\right) \label{6.3.4} \]

Os poucos níveis de energia mais baixos são mostrados na Figura\(\PageIndex{1}\). Uma das leis fundamentais da física é que a matéria é mais estável com a menor energia possível. Assim, o elétron em um átomo de hidrogênio geralmente se move na\(n = 1\) órbita, a órbita na qual ele tem a menor energia. Quando o elétron está nessa órbita de menor energia, diz-se que o átomo está em seu estado eletrônico fundamental (ou simplesmente no estado fundamental). Se o átomo receber energia de uma fonte externa, é possível que o elétron se mova para uma órbita com um\(n\) valor maior e o átomo esteja agora em um estado eletrônico excitado (ou simplesmente um estado excitado) com uma energia maior. Quando um elétron faz a transição de um estado excitado (órbita de maior energia) para um estado menos excitado, ou estado fundamental, a diferença de energia é emitida como um fóton. Da mesma forma, se um fóton é absorvido por um átomo, a energia do fóton move um elétron de uma órbita de energia mais baixa para uma mais excitada.

alt — Figura\(\PageIndex{1}\): Números quânticos e níveis de energia em um átomo de hidrogênio. Quanto mais negativo for o valor calculado, menor será a energia.

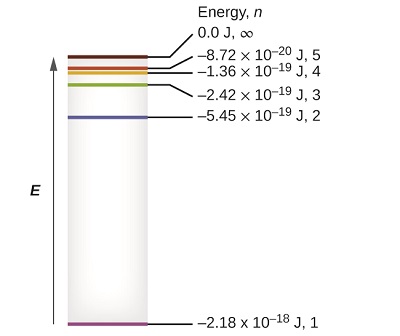
Podemos relacionar a energia dos elétrons nos átomos com o que aprendemos anteriormente sobre energia. A lei de conservação de energia diz que não podemos criar nem destruir energia. Assim, se uma certa quantidade de energia externa for necessária para excitar um elétron de um nível de energia para outro, essa mesma quantidade de energia será liberada quando o elétron retornar ao seu estado inicial (Figura\(\PageIndex{2}\)). Na verdade, um átomo pode “armazenar” energia usando-a para promover um elétron a um estado com maior energia e liberá-la quando o elétron retorna a um estado inferior. A energia pode ser liberada como um quantum de energia, à medida que o elétron retorna ao seu estado fundamental (digamos, de\(n = 5\) para\(n = 1\)), ou pode ser liberada como dois ou mais quanta menores quando o elétron cai para um estado intermediário, depois para o estado fundamental (digamos, de\(n = 5\) para\(n = 4\), emitindo um quântico, depois para\(n = 1\), emitindo um segundo quantum).

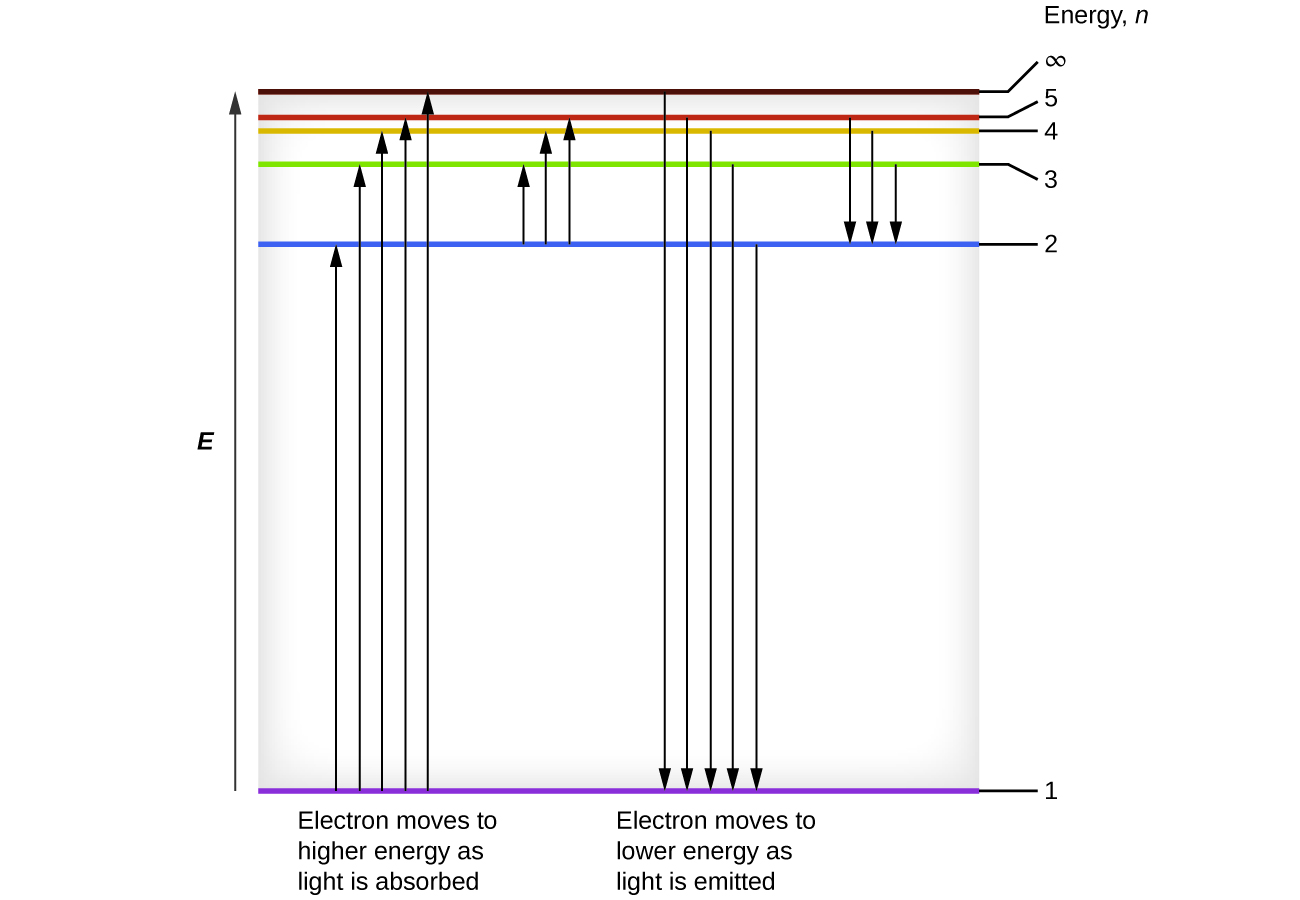
Figura\(\PageIndex{2}\): As linhas horizontais mostram a energia relativa das órbitas no modelo de Bohr do átomo de hidrogênio, e as setas verticais mostram a energia dos fótons absorvidos (à esquerda) ou emitidos (à direita) à medida que os elétrons se movem entre essas órbitas.

Como o modelo de Bohr envolvia apenas um único elétron, ele também poderia ser aplicado aos íons de elétron único He ⁺, Li ² ⁺, Be ³ ⁺ e assim por diante, que diferem do hidrogênio apenas em suas cargas nucleares, e assim os átomos e íons de um elétron são coletivamente referidos como átomos hidrogênicos ou hidrogênicos. A expressão de energia para átomos semelhantes a hidrogênio é uma generalização da energia do átomo de hidrogênio, na qual\(Z\) está a carga nuclear (+1 para hidrogênio, +2 para He, +3 para Li e assim por diante) e\(k\) tem um valor de\(2.179 \times 10^{–18}\; J\).

\[ \color{red} E_n=−\dfrac{kZ^2}{n^2} \label{6.3.5} \]

Os tamanhos das órbitas circulares para átomos semelhantes a hidrogênio são dados em termos de seus raios pela seguinte expressão, na qual\(a_o\) há uma constante chamada raio de Bohr, com um valor de\(5.292 \times 10^{−11}\; m\):

\[ \color{red} r=\dfrac{n^2}{Z} a_0 \label{6.3.6} \]

A equação também nos mostra que, à medida que a energia do elétron aumenta (à medida que\(n\) aumenta), o elétron é encontrado a maiores distâncias do núcleo. Isso está implícito\(r\) na dependência inversa do potencial de Coulomb, pois, à medida que o elétron se afasta do núcleo, a atração eletrostática entre ele e o núcleo diminui e é mantido com menos força no átomo. Observe que, à medida\(n\) que aumentam e as órbitas ficam maiores, suas energias se aproximam de zero e, portanto, os\(r⟶∞\) limites\(n⟶∞\) indicam que\(E = 0\) corresponde ao limite de ionização em que o elétron é completamente removido do núcleo. Assim, para o hidrogênio no estado fundamental\(n = 1\), a energia de ionização seria:

\[ ΔE=E_{n⟶∞} −E_1=0+k=k \label{6.3.7} \]

Com três paradoxos extremamente intrigantes agora resolvidos (radiação de corpo negro, efeito fotoelétrico e átomo de hidrogênio), e todos envolvendo a constante de Planck de maneira fundamental, ficou claro para a maioria dos físicos da época que as teorias clássicas que funcionavam tão bem no mundo macroscópico eram fundamentalmente defeituoso e não pôde ser estendido até o domínio microscópico de átomos e moléculas. Infelizmente, apesar da notável conquista de Bohr em derivar uma expressão teórica para a constante de Rydberg, ele não conseguiu estender sua teoria para o próximo átomo mais simples, He, que tem apenas dois elétrons. O modelo de Bohr tinha graves falhas, pois ainda era baseado na noção mecânica clássica de órbitas precisas, um conceito que mais tarde foi considerado insustentável no domínio microscópico, quando um modelo adequado de mecânica quântica foi desenvolvido para substituir a mecânica clássica.

Exemplo\(\PageIndex{1}\): Calculating the Energy of an Electron in a Bohr Orbit

Os primeiros pesquisadores ficaram muito entusiasmados quando conseguiram prever a energia de um elétron a uma distância específica do núcleo em um átomo de hidrogênio. Se uma faísca promove o elétron em um átomo de hidrogênio em uma órbita com\(n = 3\), qual é a energia calculada, em joules, do elétron?

Solução

A energia do elétron é dada pela equação\(\ref{6.3.5}\):

\[ E=\dfrac{−kZ^2}{n^2} \nonumber \]

O número atômico,\(Z\), do hidrogênio é 1;\(k = 2.179 \times 10^{–18}\; J\); e o elétron é caracterizado por um valor n de\(3\). Assim,

\[E=\dfrac{−(2.179 \times 10^{−18}\;J)×(1)^2}{(3)^2}=−2.421 \times 10^{−19}\;J \nonumber \]

Exercício\(\PageIndex{1}\)

O elétron em Exemplo\(\PageIndex{1}\) no\(n=3\) estado é promovido ainda mais para uma órbita com\(n = 6\). Qual é a sua nova energia?

Responda: TBD

Exemplo\(\PageIndex{2}\): Calculating Electron Transitions in a One–electron System

Qual é a energia (em joules) e o comprimento de onda (em metros) da linha no espectro do hidrogênio que representa o movimento de um elétron da órbita de Bohr com n = 4 até a órbita com n = 6? Em que parte do espectro eletromagnético encontramos essa radiação?

Solução

Nesse caso, o elétron começa com\(n = 4\), então\(n_1 = 4\). Ele vem para descansar na\(n = 6\) órbita, então\(n_2 = 6\). A diferença de energia entre os dois estados é dada por esta expressão:

\[ΔE=E_1−E_2=2.179 \times 10^{−18}\left(\dfrac{1}{n^2_1}−\dfrac{1}{n_2^2}\right) \nonumber \]

\[ΔE=2.179 \times 10^{−18} \left(\dfrac{1}{4^2}−\dfrac{1}{6^2}\right)\; J \nonumber \]

\[ΔE=2.179 \times 10^{−18} \left(\dfrac{1}{16}−\dfrac{1}{36}\right)\;J \nonumber \]

\[ΔE=7.566 \times 10^{−20}\;J \nonumber \]

Essa diferença de energia é positiva, indicando que um fóton entra no sistema (é absorvido) para excitar o elétron da órbita n = 4 até a\(n = 6\) órbita. O comprimento de onda de um fóton com essa energia é encontrado pela expressão\(E=hc \lambda\). O rearranjo dá:

\[ \lambda=\dfrac{hc}{E} \nonumber \]

A partir da figura da radiação eletromagnética, podemos ver que esse comprimento de onda é encontrado na porção infravermelha do espectro eletromagnético.

Exercício\(\PageIndex{2}\)

Qual é a energia em joules e o comprimento de onda em metros do fóton produzido quando um elétron cai do nível\(n = 5\) para o\(n = 3\) nível em um\(He^+\) íon (\(Z = 2\)for\(He^+\))?

Responda: \(6.198 \times 10^{–19}\; J\)e\(3.205 \times 10^{−7}\; m\)

O modelo de Bohr do átomo de hidrogênio fornece uma visão sobre o comportamento da matéria no nível microscópico, mas não leva em conta as interações elétron-elétron em átomos com mais de um elétron. Ele apresenta várias características importantes de todos os modelos usados para descrever a distribuição de elétrons em um átomo. Esses recursos incluem o seguinte:

As energias dos elétrons (níveis de energia) em um átomo são quantizadas, descritas por números quânticos: números inteiros com apenas um valor específico permitido e usados para caracterizar a disposição dos elétrons em um átomo.
A energia de um elétron aumenta com o aumento da distância do núcleo.
As energias discretas (linhas) nos espectros dos elementos resultam de energias eletrônicas quantizadas.

Dessas características, a mais importante é o postulado dos níveis de energia quantizados para um elétron em um átomo. Como consequência, o modelo lançou as bases para o modelo de mecânica quântica do átomo. Bohr ganhou o Prêmio Nobel de Física por suas contribuições à nossa compreensão da estrutura dos átomos e como isso está relacionado às emissões de espectros de linha.

Resumo

Bohr incorporou as ideias de quantização de Planck e Einstein em um modelo do átomo de hidrogênio que resolveu o paradoxo da estabilidade do átomo e dos espectros discretos. O modelo de Bohr do átomo de hidrogênio explica a conexão entre a quantização de fótons e a emissão quantizada dos átomos. Bohr descreveu o átomo de hidrogênio em termos de um elétron se movendo em uma órbita circular em torno de um núcleo. Ele postulou que o elétron estava restrito a certas órbitas caracterizadas por energias discretas. As transições entre essas órbitas permitidas resultam na absorção ou emissão de fótons. Quando um elétron se move de uma órbita de maior energia para uma mais estável, a energia é emitida na forma de um fóton. Para mover um elétron de uma órbita estável para uma mais excitada, um fóton de energia deve ser absorvido. Usando o modelo de Bohr, podemos calcular a energia de um elétron e o raio de sua órbita em qualquer sistema de um elétron.

Glossário

Modelo de Bohr do átomo de hidrogênio: modelo estrutural em que um elétron se move ao redor do núcleo somente em órbitas circulares, cada uma com um raio específico permitido; o elétron em órbita normalmente não emite radiação eletromagnética, mas o faz ao mudar de uma órbita para outra.

estado de excitação: estado com uma energia maior do que a energia do estado fundamental

estado fundamental: estado em que os elétrons em um átomo, íon ou molécula têm a menor energia possível

número quântico: número inteiro com apenas valores específicos permitidos e usado para caracterizar a disposição dos elétrons em um átomo