12.4: A equação de regressão

Os dados raramente se encaixam exatamente em uma linha reta. Normalmente, você deve estar satisfeito com previsões aproximadas. Normalmente, você tem um conjunto de dados cujo gráfico de dispersão parece “caber” em uma linha reta. Isso é chamado de Linha de Melhor Ajuste ou Linha de Menos Quadrados.

EXERCÍCIO COLABORATIVO

Se você conhece o comprimento do dedo mindinho (menor) de uma pessoa, acha que poderia prever a altura dessa pessoa? Colete dados da sua turma (comprimento do dedo mindinho, em polegadas). A variável independente,\(x\), é o comprimento do dedo mindinho e a variável dependente,\(y\), é a altura. Para cada conjunto de dados, plote os pontos em papel quadriculado. Faça seu gráfico grande o suficiente e use uma régua. Em seguida, “a olho nu”, desenhe uma linha que pareça “caber” nos dados. Para sua linha, escolha dois pontos convenientes e use-os para encontrar a inclinação da linha. Encontre o\(y\) intercepto -da linha estendendo sua linha para que ela cruze o\(y\) eixo -. Usando as inclinações e as\(y\) interceptações -, escreva sua equação de “melhor ajuste”. Você acha que todos terão a mesma equação? Por que ou por que não? De acordo com sua equação, qual é a altura prevista para um comprimento mindinho de 2,5 polegadas?

Exemplo\(\PageIndex{1}\)

Uma amostra aleatória de 11 estudantes de estatística produziu os seguintes dados, onde\(x\) é a pontuação do terceiro exame de 80 e\(y\) a nota final do exame de 200. Você pode prever a pontuação final do exame de um aluno aleatório se souber a pontuação do terceiro exame?

1a: Tabela mostrando as notas do exame final com base nas notas do terceiro exame.

\(x\)(nota do terceiro exame)	\(y\)(nota final do exame)
\ (x\) (nota do terceiro exame) ">65	\ (y\) (nota do exame final) ">175
\ (x\) (nota do terceiro exame) ">67	\ (y\) (nota final do exame) ">133
\ (x\) (nota do terceiro exame) ">71	\ (y\) (nota do exame final) ">185
\ (x\) (nota do terceiro exame) ">71	\ (y\) (nota do exame final) ">163
\ (x\) (nota do terceiro exame) ">66	\ (y\) (nota do exame final) ">126
\ (x\) (nota do terceiro exame) ">75	\ (y\) (nota final do exame) ">198
\ (x\) (nota do terceiro exame) ">67	\ (y\) (nota do exame final) ">153
\ (x\) (nota do terceiro exame) ">70	\ (y\) (nota do exame final) ">163
\ (x\) (nota do terceiro exame) ">71	\ (y\) (nota final do exame) ">159
\ (x\) (nota do terceiro exame) ">69	\ (y\) (nota do exame final) ">151
\ (x\) (nota do terceiro exame) ">69	\ (y\) (nota final do exame) ">159

Figura\(\PageIndex{1}\): Gráfico de dispersão mostrando as pontuações do exame final com base nas pontuações do terceiro exame.

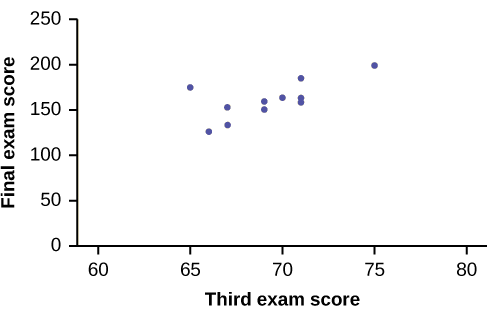
Exercício\(\PageIndex{1}\)

Os mergulhadores têm tempos máximos de mergulho que não podem exceder quando vão a profundidades diferentes. Os dados na Tabela mostram diferentes profundidades com os tempos máximos de mergulho em minutos. Use sua calculadora para encontrar a linha de regressão de mínimos quadrados e prever o tempo máximo de mergulho para 110 pés.

\(X\)(profundidade em pés)	\(Y\)(tempo máximo de mergulho)
\ (X\) (profundidade em pés) ">50	\ (Y\) (tempo máximo de mergulho) ">80
\ (X\) (profundidade em pés) ">60	\ (Y\) (tempo máximo de mergulho) ">55
\ (X\) (profundidade em pés) ">70	\ (Y\) (tempo máximo de mergulho) ">45
\ (X\) (profundidade em pés) ">80	\ (Y\) (tempo máximo de mergulho) ">35
\ (X\) (profundidade em pés) ">90	\ (Y\) (tempo máximo de mergulho) ">25
\ (X\) (profundidade em pés) ">100	\ (Y\) (tempo máximo de mergulho) ">22

Responda

\(\hat{y} = 127.24 – 1.11x\)

A 110 pés, um mergulhador podia mergulhar por apenas cinco minutos.

A pontuação do terceiro exame,\(x\), é a variável independente e a pontuação final do exame,\(y\), é a variável dependente. Traçaremos uma linha de regressão que melhor “se ajusta” aos dados. Se cada um de vocês encaixasse uma linha “a olho nu”, desenharia linhas diferentes. Podemos usar o que é chamado de linha de regressão de mínimos quadrados para obter a linha de melhor ajuste.

Considere o diagrama a seguir. Cada ponto de dados tem a forma (\(x, y\)) e cada ponto da linha de melhor ajuste usando regressão linear de mínimos quadrados tem a forma (\(x, \hat{y}\)).

O\(\hat{y}\) é lido como “\(y\)chapéu” e é o valor estimado de\(y\). É o valor\(y\) obtido usando a linha de regressão. Geralmente, não é igual aos dados\(y\) obtidos.

Figura\(\PageIndex{2}\)

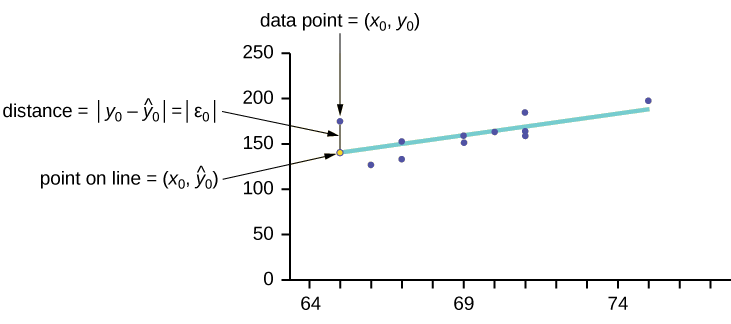
O termo\(y_{0} – \hat{y}_{0} = \varepsilon_{0}\) é chamado de “erro” ou residual. Não é um erro no sentido de um erro. O valor absoluto de um resíduo mede a distância vertical entre o valor real de\(y\) e o valor estimado de\(y\). Em outras palavras, ele mede a distância vertical entre o ponto de dados real e o ponto previsto na linha.

Se o ponto de dados observado estiver acima da linha, o resíduo será positivo e a linha subestima o valor real dos dados para\(y\). Se o ponto de dados observado estiver abaixo da linha, o resíduo será negativo e a linha superestima o valor real dos dados para\(y\).

No diagrama da Figura,\(y_{0} – \hat{y}_{0} = \varepsilon_{0}\) é o resíduo do ponto mostrado. Aqui, o ponto está acima da linha e o resíduo é positivo.

\(\varepsilon =\)a letra grega épsilon

Para cada ponto de dados, você pode calcular os resíduos ou erros,\(y_{i} - \hat{y}_{i} = \varepsilon_{i}\) para\(i = 1, 2, 3, ..., 11\).

Cada um\(|\varepsilon|\) é uma distância vertical.

Para o exemplo sobre as notas do terceiro exame e as notas do exame final dos 11 estudantes de estatística, existem 11 pontos de dados. Portanto, existem 11\(\varepsilon\) valores. Se você quadrar cada um\(\varepsilon\) e somar, você obtém

\[(\varepsilon_{1})^{2} + (\varepsilon_{2})^{2} + \dotso + (\varepsilon_{11})^{2} = \sum^{11}_{i = 1} \varepsilon^{2} \label{SSE}\]

A equação\ ref {SSE} é chamada de Soma dos Quadrados de Erros (SSE).

Usando o cálculo, você pode determinar os valores de\(a\) e\(b\) que tornam o SSE mínimo. Ao reduzir o SSE ao mínimo, você determinou os pontos que estão na linha de melhor ajuste. Acontece que a linha de melhor ajuste tem a equação:

\[\hat{y} = a + bx\]

onde

• \(a = \bar{y} - b\bar{x}\)e
• \(b = \dfrac{\sum(x - \bar{x})(y - \bar{y})}{\sum(x - \bar{x})^{2}}\).

As médias amostrais dos\(x\) valores e dos\(x\) valores são\(\bar{x}\) e\(\bar{y}\), respectivamente. A linha de melhor ajuste sempre passa pelo ponto\((\bar{x}, \bar{y})\).

A inclinação\(b\) pode ser escrita como\(b = r\left(\dfrac{s_{y}}{s_{x}}\right)\) onde\(s_{y} =\) o desvio padrão dos\(y\) valores e\(s_{x} =\) o desvio padrão dos\(x\) valores. \(r\)é o coeficiente de correlação, que será discutido na próxima seção.

Critérios mínimos quadrados para melhor ajuste

O processo de ajuste da linha de melhor ajuste é chamado de regressão linear. A ideia por trás de encontrar a linha mais adequada é baseada na suposição de que os dados estão espalhados por uma linha reta. O critério para a melhor linha de ajuste é que a soma dos erros quadrados (SSE) seja minimizada, ou seja, feita o menor possível. Qualquer outra linha que você escolher teria um SSE maior do que a linha de melhor ajuste. Essa linha de melhor ajuste é chamada de linha de regressão de mínimos quadrados.

Nota

Planilhas de computador, software estatístico e muitas calculadoras podem calcular rapidamente a linha mais adequada e criar os gráficos. Os cálculos tendem a ser entediantes se feitos à mão. As instruções para usar as calculadoras TI-83, TI-83+ e TI-84+ para encontrar a linha mais adequada e criar um gráfico de dispersão são mostradas no final desta seção.

EXEMPLO DE TERCEIRO EXAME versus EXAME FINAL:

O gráfico da linha de melhor ajuste para o exemplo do terceiro exame/exame final é o seguinte:

Figura\(\PageIndex{3}\)

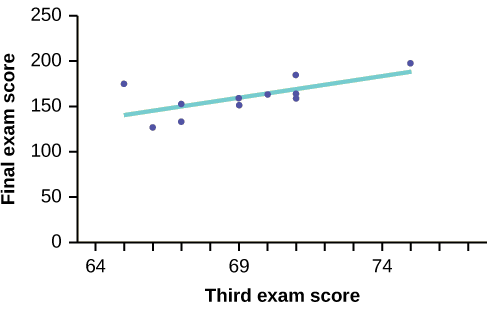
A linha de regressão de mínimos quadrados (linha de melhor ajuste) para o exemplo do terceiro exame/exame final tem a equação:

\[\hat{y} = -173.51 + 4.83x\]

LEMBRETE

Lembre-se de que é sempre importante traçar primeiro um diagrama de dispersão. Se o gráfico de dispersão indicar que há uma relação linear entre as variáveis, então é razoável usar uma linha de melhor ajuste para fazer previsões para\(y\) dados\(x\) dentro do domínio de\(x\) -valores nos dados de amostra, mas não necessariamente para valores de x externos esse domínio. Você pode usar a linha para prever a pontuação final do exame para um aluno que obteve uma nota de 73 no terceiro exame. Você NÃO deve usar a linha para prever a pontuação final do exame para um aluno que obteve uma nota de 50 no terceiro exame, porque 50 não está dentro do domínio dos\(x\) valores -nos dados da amostra, que estão entre 65 e 75.

Entendendo a inclinação

A inclinação da linha,\(b\), descreve como as mudanças nas variáveis estão relacionadas. É importante interpretar a inclinação da linha no contexto da situação representada pelos dados. Você deve ser capaz de escrever uma frase interpretando a inclinação em inglês simples.

INTERPRETAÇÃO DA INCLINAÇÃO: A inclinação da linha de melhor ajuste nos diz como a variável dependente (\(y\)) muda para cada aumento de uma unidade na variável independente (\(x\)), em média.

EXEMPLO DE TERCEIRO EXAME versus EXAME FINAL

Inclinação: A inclinação da linha é\(b = 4.83\).

Interpretação: Para um aumento de um ponto na pontuação do terceiro exame, a pontuação final do exame aumenta em 4,83 pontos, em média.

USANDO A CALCULADORA TI-83, 83+, 84, 84+

Usando o teste T de regressão linear: LinRegtTest

1. No editor de listas STAT, insira os\(X\) dados na lista L1 e os dados Y na lista L2, emparelhados de forma que os valores correspondentes (\(x,y\)) fiquem próximos uns dos outros nas listas. (Se um determinado par de valores for repetido, insira-o quantas vezes ele aparecer nos dados.)
2. No menu STAT TESTS, role para baixo com o cursor para selecionar o LinRegtTest. (Tenha cuidado ao selecionar LinRegtTest, pois algumas calculadoras também podem ter um item diferente chamado LinRegtint.)
3. Na tela de entrada LinRegtTest, digite: Xlist: L1; Ylist: L2; Freq: 1
4. Na próxima linha, no prompt\(\beta\) ou\(\rho\), destaque "\(\neq 0\)" e pressione ENTER
5. Deixe a linha para “RegEq:” em branco
6. Destaque Calcular e pressione ENTER.

Figura\(\PageIndex{4}\)

A tela de saída contém muitas informações. Por enquanto, vamos nos concentrar em alguns itens da saída e retornaremos posteriormente aos outros itens.

A segunda linha diz\(y = a + bx\). Role para baixo para encontrar\(a = -173.513\) os valores e\(b = 4.8273\); a equação da linha de melhor ajuste é\(\hat{y} = -173.51 + 4.83x\)

Os dois itens na parte inferior são\(r_{2} = 0.43969\)\(r = 0.663\) e. Por enquanto, basta observar onde encontrar esses valores; nós os discutiremos nas próximas duas seções.

Representação gráfica do gráfico de dispersão e da linha de regressão

1. Estamos assumindo que seus\(X\) dados já foram inseridos na lista L1 e seus\(Y\) dados estão na lista L2
2. Pressione o 2º STATPLOT ENTER para usar o Gráfico 1
3. Na tela de entrada do PLOT 1, destaque On e pressione ENTER
4. Para TIPO: destaque o primeiro ícone que é o gráfico de dispersão e pressione ENTER
5. Indique a lista X: L1 e a lista Y: L2
6. Para Mark: não importa qual símbolo você destaca.
7. Pressione a tecla ZOOM e depois o número 9 (para o item de menu “ZoomStat”); a calculadora ajustará a janela aos dados
8. Para representar graficamente a linha de melhor ajuste, pressione a tecla\(Y =\) "" e digite a equação\(-173.5 + 4.83X\) na equação Y1. (A\(X\) chave fica imediatamente à esquerda da tecla STAT). Pressione ZOOM 9 novamente para representar graficamente.
9. Opcional: Se você quiser alterar a janela de visualização, pressione a tecla WINDOW. Entre na janela desejada usando Xmin, Xmax, Ymin, Ymax

Nota

Outra forma de representar graficamente a linha depois de criar um gráfico de dispersão é usar LinRegtTest.

1. Certifique-se de ter feito o gráfico de dispersão. Verifique na sua tela.
2. Vá para LinRegtTest e entre nas listas.
3. Em RegEq: pressione VARS e flecha até Y-VARS. Pressione 1 para 1: Função. Pressione 1 para 1:Y1. Em seguida, seta para baixo até Calcular e faça o cálculo para a linha de melhor ajuste.
4. Imprensa\(Y = (\text{you will see the regression equation})\).
5. Pressione GRAPH. A linha será traçada.”

O coeficiente de correlação\(r\)

Além de observar o gráfico de dispersão e ver que uma linha parece razoável, como saber se a linha é um bom preditor? Use o coeficiente de correlação como outro indicador (além do gráfico de dispersão) da força da relação entre\(x\)\(y\) e. O coeficiente de correlação\(r\), desenvolvido por Karl Pearson no início dos anos 1900, é numérico e fornece uma medida de força e direção da associação linear entre a variável independente\(x\) e a variável dependente\(y\).

O coeficiente de correlação é calculado como

\[r = \dfrac{n \sum(xy) - \left(\sum x\right)\left(\sum y\right)}{\sqrt{\left[n \sum x^{2} - \left(\sum x\right)^{2}\right] \left[n \sum y^{2} - \left(\sum y\right)^{2}\right]}}\]

onde\(n =\) o número de pontos de dados.

Se você suspeitar de uma relação linear entre\(x\) e\(y\), então\(r\) pode medir o quão forte é a relação linear.

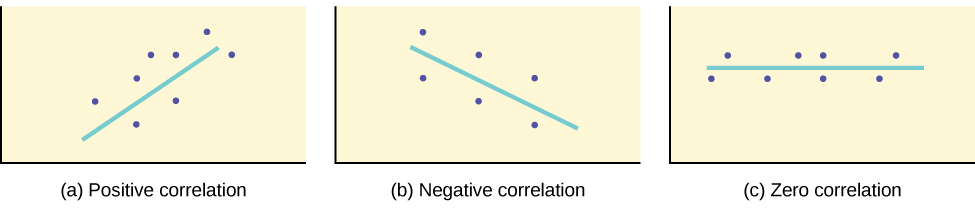
O que o VALOR do nos\(r\) diz:

• O valor de\(r\) está sempre entre —1 e +1: —1 ≤ r ≤ 1.
• O tamanho da correlação\(r\) indica a força da relação linear entre\(x\)\(y\) e. Valores\(r\) próximos a —1 ou +1 indicam uma relação linear mais forte entre\(x\)\(y\) e.
• Se não\(r = 0\) houver absolutamente nenhuma relação linear entre\(x\) e\(y\) (sem correlação linear).
• Se\(r = 1\), existe uma correlação positiva perfeita. Se\(r = -1\), existe uma correlação negativa perfeita. Em ambos os casos, todos os pontos de dados originais estão em uma linha reta. É claro que, no mundo real, isso geralmente não acontece.

O que o SIGNO de nos\(r\) diz:

• Um valor positivo de\(r\) significa que quando\(x\) aumenta,\(y\) tende a aumentar e quando\(x\) diminui,\(y\) tende a diminuir (correlação positiva).
• Um valor negativo de\(r\) significa que quando\(x\) aumenta,\(y\) tende a diminuir e quando\(x\) diminui,\(y\) tende a aumentar (correlação negativa).
• O sinal de\(r\) é o mesmo que o sinal da inclinação,\(b\), da linha de melhor ajuste.

Nota

Uma forte correlação não sugere essas\(x\) causas\(y\) ou\(y\) causas\(x\). Dizemos que “correlação não implica causalidade”.

Figura\(\PageIndex{5}\): (a) Um gráfico de dispersão mostrando dados com uma correlação positiva. \(0 < r < 1\)(b) Um gráfico de dispersão mostrando dados com uma correlação negativa. \(-1 < r < 0\)(c) Um gráfico de dispersão mostrando dados com correlação zero. \(r = 0\)

A fórmula para\(r\) parece formidável. No entanto, planilhas de computador, software estatístico e muitas calculadoras podem calcular rapidamente\(r\). O coeficiente de correlação\(r\) é o item inferior nas telas de saída do LinRegtTest na calculadora TI-83, TI-83+ ou TI-84+ (consulte a seção anterior para obter instruções).

O coeficiente de determinação

A variável\(r^{2}\) é chamada de coeficiente de determinação e é o quadrado do coeficiente de correlação, mas geralmente é declarada como uma porcentagem, em vez de na forma decimal. Tem uma interpretação no contexto dos dados:

• \(r^{2}\), quando expresso como uma porcentagem, representa a porcentagem de variação na variável dependente (prevista)\(y\) que pode ser explicada pela variação na variável independente (explicativa)\(x\) usando a linha de regressão (melhor ajuste).
• \(1 - r^{2}\), quando expresso como uma porcentagem, representa o percentual de variação\(y\) que NÃO é explicado pela variação no\(x\) uso da linha de regressão. Isso pode ser visto como a dispersão dos pontos de dados observados sobre a linha de regressão.

Considere o exemplo do terceiro exame/exame final apresentado na seção anterior

• A linha de melhor ajuste é:\(\hat{y} = -173.51 + 4.83x\)
• O coeficiente de correlação é\(r = 0.6631\)
• O coeficiente de determinação é\(r^{2} = 0.6631^{2} = 0.4397\)
• Interpretação de\(r^{2}\) no contexto deste exemplo:
• Aproximadamente 44% da variação (0,4397 é aproximadamente 0,44) nas notas do exame final pode ser explicada pela variação nas notas do terceiro exame, usando a linha de regressão de melhor ajuste.
• Portanto, aproximadamente 56% da variação (\(1 - 0.44 = 0.56\)) nas notas do exame final NÃO pode ser explicada pela variação nas notas do terceiro exame, usando a linha de regressão de melhor ajuste. (Isso é visto como a dispersão dos pontos ao redor da linha.)

Resumo

Uma linha de regressão, ou uma linha de melhor ajuste, pode ser desenhada em um gráfico de dispersão e usada para prever resultados para as\(y\) variáveis\(x\) e em um determinado conjunto de dados ou dados de amostra. Há várias maneiras de encontrar uma linha de regressão, mas geralmente a linha de regressão de mínimos quadrados é usada porque ela cria uma linha uniforme. Os resíduos, também chamados de “erros”, medem a distância do valor real\(y\) e o valor estimado de\(y\). A Soma dos Erros Quadrados, quando definida como seu mínimo, calcula os pontos na linha de melhor ajuste. As linhas de regressão podem ser usadas para prever valores dentro de um determinado conjunto de dados, mas não devem ser usadas para fazer previsões de valores fora do conjunto de dados.

O coeficiente de correlação\(r\) mede a força da associação linear entre\(x\)\(y\) e. A variável\(r\) deve estar entre —1 e +1. Quando\(r\) é positivo, o\(x\) e\(y\) tenderá a aumentar e diminuir em conjunto. Quando\(r\) é negativo,\(x\) aumentará e\(y\) diminuirá, ou o contrário,\(x\)\(y\) diminuirá e aumentará. O coeficiente de determinação\(r^{2}\) é igual ao quadrado do coeficiente de correlação. Quando expresso como uma porcentagem,\(r^{2}\) representa a porcentagem de variação na variável dependente\(y\) que pode ser explicada pela variação na variável independente\(x\) usando a linha de regressão.

Glossário

Coeficiente de correlação

uma medida desenvolvida por Karl Pearson (início dos anos 1900) que fornece a força da associação entre a variável independente e a variável dependente; a fórmula é:

\[r = \dfrac{n \sum xy - \left(\sum x\right) \left(\sum y\right)}{\sqrt{\left[n \sum x^{2} - \left(\sum x\right)^{2}\right] \left[n \sum y^{2} - \left(\sum y\right)^{2}\right]}}\]

onde\(n\) está o número de pontos de dados. O coeficiente não pode ser maior que 1 ou menor que —1. Quanto mais próximo o coeficiente estiver de ±1, mais forte será a evidência de uma relação linear significativa entre\(x\)\(y\) e.