Skip to main content
Global

6.2: A distribuição normal padrão

  1. Last updated
  2. Save as PDF
  • Page ID
    190231

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Pontuações Z

    A distribuição normal padrão é uma distribuição normal de valores padronizados chamados escores-z. A pontuação z é medida em unidades do desvio padrão.

    Definição: Z-Score

    Se\(X\) for uma variável aleatória normalmente distribuída e\(X \sim N(\mu, \sigma)\), então, a pontuação z é:

    \[z = \dfrac{x - \mu}{\sigma} \label{zscore}\]

    A pontuação z indica quantos desvios padrão o valor\(x\) está acima (à direita) ou abaixo (à esquerda) da média,\(\mu\). Valores maiores do que a média têm\(z\) pontuações positivas, e valores menores do\(x\) que a média têm\(z\) pontuações negativas.\(x\) Se for\(x\) igual à média, então\(x\) tem uma\(z\) pontuação de zero. Por exemplo, se a média de uma distribuição normal for cinco e o desvio padrão for dois, o valor 11 será três desvios padrão acima (ou à direita) da média. O cálculo é o seguinte:

    \[ \begin{align*} x &= \mu + (z)(\sigma) \\[5pt] &= 5 + (3)(2) = 11 \end{align*}\]

    A pontuação z é três.

    Como a média da distribuição normal padrão é zero e o desvio padrão é um, a transformação na Equação\ ref {zscore} produz a distribuição\(Z \sim N(0, 1)\). O valor\(x\) vem de uma distribuição normal com média\(\mu\) e desvio padrão\(\sigma\).

    A pontuação z é medida em unidades do desvio padrão.

    Exemplo\(\PageIndex{1}\)

    Suponha\(X \sim N(5, 6)\). Isso diz que\(x\) é uma variável aleatória normalmente distribuída com média\(\mu = 5\) e desvio padrão\(\sigma = 6\). Suponha\(x = 17\). Então (via Equation\ ref {zscore}):

    \[z = \dfrac{x-\mu}{\sigma} = \dfrac{17-5}{6} = 2 \nonumber\]

    Isso significa que\(x = 17\) há dois desvios padrão (2\(\sigma\)) acima ou à direita da média\(\mu = 5\). O desvio padrão é\(\sigma = 6\).

    Observe que:\(5 + (2)(6) = 17\) (O padrão é\(\mu + z \sigma = x\))

    Agora, suponha\(x = 1\). Então:

    \[z = \dfrac{x-\mu}{\sigma} = \dfrac{1-5}{6} = -0.67 \nonumber\]

    (arredondado para duas casas decimais)

    Isso significa que\(x = 1\) são desvios\(0.67\) padrão (\(–0.67\sigma\)) abaixo ou à esquerda da média\(\mu = 5\). Observe que:\(5 + (–0.67)(6)\) é aproximadamente igual a um (Isso tem o padrão\(\mu + (–0.67)\sigma = 1\))

    Resumindo, quando\(z\) é positivo,\(x\) está acima ou à direita de\(\mu\) e quando\(z\) é negativo,\(x\) está à esquerda ou abaixo\(\mu\). Ou, quando\(z\) é positivo,\(x\) é maior que\(\mu\), e quando\(z\) é negativo\(x\) é menor que\(\mu\).

    Exercício\(\PageIndex{1}\)

    Qual é a\(z\) pontuação -de\(x\), quando\(x = 1\) e\(X \sim N(12, 3)\)?

    Resposta

    \(z = \dfrac{1-12}{3} \approx -3.67\)

    Exemplo\(\PageIndex{2}\)

    Alguns médicos acreditam que uma pessoa pode perder cinco quilos, em média, em um mês, reduzindo a ingestão de gordura e se exercitando de forma consistente. Suponha que a perda de peso tenha uma distribuição normal. Deixe\(X =\) a quantidade de peso perdida (em libras) por uma pessoa em um mês. Use um desvio padrão de duas libras. \(X \sim N(5, 2)\). Preencha os espaços em branco.

    1. Suponha que uma pessoa tenha perdido dez libras em um mês. A\(z\) pontuação -quando\(x = 10\) as libras são\(x = 2.5\) (verifique). Essa\(z\) pontuação indica que ________\(x = 10\) são desvios padrão para ________ (direita ou esquerda) da média _____ (Qual é a média?).
    2. Suponha que uma pessoa ganhe três quilos (uma perda de peso negativa). Então\(z =\) __________. Essa\(z\) pontuação indica que\(x = -3\) são ________ desvios padrão para __________ (direita ou esquerda) da média.

    Respostas

    a. Essa\(z\) pontuação indica que\(x = 10\) são 2,5 desvios padrão à direita da média de cinco.

    b. Suponha as variáveis aleatórias\(X\) e\(Y\) tenha as seguintes distribuições normais:\(X \sim N(5, 6)\)\(Y \sim N(2, 1)\) e. Se\(x = 17\), então\(z = 2\). (Isso foi mostrado anteriormente.) Se\(y = 4\), o que é\(z\)?

    \[z = \dfrac{y-\mu}{\sigma} = \dfrac{4-2}{1} = 2 \nonumber\]

    onde\(\mu = 2\)\(\sigma = 1\) e.

    A\(z\) pontuação -para\(y = 4\) é\(z = 2\). Isso significa que quatro são desvios\(z = 2\) padrão à direita da média. Portanto,\(x = 17\) e ambos\(y = 4\) são dois (próprios) desvios padrão à direita de suas respectivas médias.

    A pontuação z nos permite comparar dados que são escalados de forma diferente. Para entender o conceito, suponha que\(X \sim N(5, 6)\) represente ganhos de peso para um grupo de pessoas que estão tentando ganhar peso em um período de seis semanas e\(Y \sim N(2, 1)\) mede o mesmo ganho de peso para um segundo grupo de pessoas. Um ganho de peso negativo seria uma perda de peso. Como\(x = 17\) cada um\(y = 4\) deles tem dois desvios padrão à direita de suas médias, eles representam o mesmo ganho de peso padronizado em relação às suas médias.

    Exercício\(\PageIndex{2}\)

    Preencha os espaços em branco.

    Jerome tem uma média de 16 pontos por jogo com um desvio padrão de quatro pontos. \(X \sim N(16, 4)\). Suponha que Jerome marque dez pontos em um jogo. O\(z\) —score quando\(x = 10\) é\(-1.5\). Essa pontuação indica que\(x = 10\) são _____ desvios padrão para ______ (direita ou esquerda) da média______ (Qual é a média?).

    Resposta

    1,5, esquerda, 16

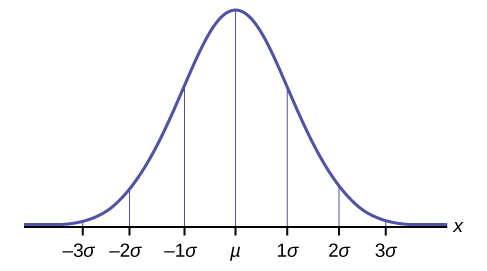
    A regra empírica

    Se\(X\) for uma variável aleatória e tiver uma distribuição normal com média\(\mu\) e desvio padrão\(\sigma\), a Regra Empírica diz o seguinte:

    • Cerca de 68% dos\(x\) valores estão entre —1\(\sigma\) e +1\(\sigma\) da média\(\mu\) (dentro de um desvio padrão da média).
    • Cerca de 95% dos\(x\) valores estão entre —2\(\sigma\) e +2\(\sigma\) da média\(\mu\) (dentro de dois desvios padrão da média).
    • Cerca de 99,7% dos\(x\) valores estão entre —3\(\sigma\) e +3\(\sigma\) da média\(\mu\) (dentro de três desvios padrão da média). Observe que quase todos os\(x\) valores estão dentro de três desvios padrão da média.
    • As\(z\) pontuações -para +1\(\sigma\) e —1\(\sigma\) são +1 e —1, respectivamente.
    • As\(z\) pontuações -para +2\(\sigma\) e —2\(\sigma\) são +2 e —2, respectivamente.
    • As\(z\) pontuações -para +3\(\sigma\) e —3\(\sigma\) são +3 e —3, respectivamente.

    A regra empírica também é conhecida como regra 68-95-99,7.

    alt
    Figura\(\PageIndex{1}\)

    Exemplo\(\PageIndex{3}\)

    A altura média de homens de 15 a 18 anos do Chile de 2009 a 2010 foi de 170 cm com um desvio padrão de 6,28 cm. Sabe-se que as alturas masculinas seguem uma distribuição normal. Deixe\(X =\) a altura de um homem de 15 a 18 anos do Chile em 2009 a 2010. Então\(X \sim N(170, 6.28)\).

    1. Suponha que um homem de 15 a 18 anos do Chile tivesse 168 cm de altura de 2009 a 2010. A\(z\) pontuação -quando\(x = 168\) cm é\(z =\) _______. Essa\(z\) pontuação indica que ________\(x = 168\) são desvios padrão para ________ (direita ou esquerda) da média _____ (Qual é a média?).
    2. Suponha que a altura de um homem de 15 a 18 anos do Chile de 2009 a 2010 tenha uma\(z\) pontuação de\(z = 1.27\). Qual é a altura do homem? O\(z\) -score (\(z = 1.27\)) indica que a altura do homem é ________ desvios padrão em relação a __________ (direita ou esquerda) da média.

    Respostas

    1. —0,32, 0,32, esquerda, 170
    2. 177,98, 1,27, certo

    Exercício\(\PageIndex{3}\)

    Use as informações em Exemplo\(\PageIndex{3}\) para responder às seguintes perguntas.

    1. Suponha que um homem de 15 a 18 anos do Chile tivesse 176 cm de altura de 2009 a 2010. A\(z\) pontuação -quando\(x = 176\) cm é\(z =\) _______. Essa\(z\) pontuação indica que\(x = 176\) cm é ________ desvios padrão para ________ (direita ou esquerda) da média _____ (Qual é a média?).
    2. Suponha que a altura de um homem de 15 a 18 anos do Chile de 2009 a 2010 tenha uma\(z\) pontuação de\(z = –2\). Qual é a altura do homem? O\(z\) -score (\(z = –2\)) indica que a altura do homem é ________ desvios padrão em relação a __________ (direita ou esquerda) da média.
    Resposta

    Resolva a equação\(z = \dfrac{x-\mu}{\sigma}\) para\(z\). \(x = \mu+ (z)(\sigma)\)

    \(z = \dfrac{176-170}{6.28}\), Essa pontuação z indica que\(x = 176\) cm é 0,96 desvios padrão à direita da média de 170 cm.

    Resposta

    Resolva a equação\(z = \dfrac{x-\mu}{\sigma}\) para\(z\). \(x = \mu+ (z)(\sigma)\)

    \(X = 157.44\)cm, O\(z\) -score (\(z = –2\)) indica que a altura do homem é dois desvios padrão à esquerda da média.

    Exemplo\(\PageIndex{4}\)

    De 1984 a 1985, a altura média dos homens de 15 a 18 anos do Chile foi de 172,36 cm e o desvio padrão foi de 6,34 cm. Deixe\(Y =\) a altura de homens de 15 a 18 anos de idade de 1984 a 1985. Então\(Y \sim N(172.36, 6.34)\).

    A altura média de homens de 15 a 18 anos do Chile de 2009 a 2010 foi de 170 cm com um desvio padrão de 6,28 cm. Sabe-se que as alturas masculinas seguem uma distribuição normal. Deixe\(X =\) a altura de um homem de 15 a 18 anos do Chile em 2009 a 2010. Então\(X \sim N(170, 6.28)\).

    Encontre as pontuações z para\(x = 160.58\) cm e\(y = 162.85\) cm. Interprete cada\(z\) pontuação. O que você pode dizer sobre\(x = 160.58\) cm e\(y = 162.85\) cm?

    Resposta

    • O\(z\) -score (Equação\ ref {zscore}) para\(x = 160.58\) é\(z = –1.5\).
    • A\(z\) pontuação -para\(y = 162.85\) é\(z = –1.5\).

    Ambos\(x = 160.58\) e\(y = 162.85\) desviam o mesmo número de desvios padrão de suas respectivas médias e na mesma direção.

    Exercício\(\PageIndex{4}\)

    Em 2012, 1.664.479 estudantes fizeram o exame SAT. A distribuição dos escores na seção verbal do SAT teve uma média\(\mu = 496\) e um desvio padrão\(\sigma = 114\). Deixe\(X =\) uma pontuação na seção verbal do exame SAT em 2012. Então\(X \sim N(496, 114)\).

    Encontre as\(z\) pontuações -para\(x_{1} = 325\)\(x_{2} = 366.21\) e. Interprete cada\(z\) pontuação. O que você pode dizer sobre\(x_{1} = 325\) e\(x_{2} = 366.21\)?

    Resposta

    A pontuação z (Equação\ ref {zscore}) para\(x_{1} = 325\) é\(z_{1} = –1.15\).

    A pontuação z (Equação\ ref {zscore}) para\(x_{2} = 366.21\) é\(z_{2} = –1.14\).

    O Estudante 2 obteve uma pontuação mais próxima da média do que o Estudante 1 e, como ambos tiveram\(z\) pontuações negativas, o Estudante 2 teve a melhor pontuação.

    Exemplo\(\PageIndex{5}\)

    Suponha que x tenha uma distribuição normal com média 50 e desvio padrão 6.

    • Cerca de 68% dos valores de x estão dentro de um desvio padrão da média. Portanto, cerca de 68% dos valores de x estão entre —1σ = (—1) (6) = —6 e 1σ = (1) (6) = 6 da média de 50. Os valores 50 — 6 = 44 e 50 + 6 = 56 estão dentro de um desvio padrão da média 50. As pontuações z são —1 e +1 para 44 e 56, respectivamente.
    • Cerca de 95% dos valores de x estão dentro de dois desvios padrão da média. Portanto, cerca de 95% dos valores de x estão entre —2σ = (—2) (6) = —12 e 2σ = (2) (6) = 12. Os valores 50 — 12 = 38 e 50 + 12 = 62 estão dentro de dois desvios padrão da média 50. As pontuações z são —2 e +2 para 38 e 62, respectivamente.
    • Cerca de 99,7% dos valores de x estão dentro de três desvios padrão da média. Portanto, cerca de 99,7% dos valores de x estão entre —3σ = (—3) (6) = —18 e 3σ = (3) (6) = 18 da média de 50. Os valores 50 — 18 = 32 e 50 + 18 = 68 estão dentro de três desvios padrão da média 50. As pontuações z são —3 e +3 para 32 e 68, respectivamente.

    Exercício\(\PageIndex{5}\)

    Suponha que\(X\) tenha uma distribuição normal com média 25 e desvio padrão cinco. Entre quais valores de\(x\) 68% dos valores estão?

    Resposta

    entre 20 e 30.

    Exemplo\(\PageIndex{6}\)

    De 1984 a 1985, a altura média dos homens de 15 a 18 anos do Chile foi de 172,36 cm e o desvio padrão foi de 6,34 cm. Deixe\(Y =\) a altura de homens de 15 a 18 anos em 1984 a 1985. Então\(Y \sim N(172.36, 6.34)\).

    1. Cerca de 68% dos\(y\) valores estão entre quais dois valores? Esses valores são ________________. As\(z\) pontuações -são ________________, respectivamente.
    2. Cerca de 95% dos\(y\) valores estão entre quais dois valores? Esses valores são ________________. As\(z\) pontuações -são ________________ respectivamente.
    3. Cerca de 99,7% dos\(y\) valores estão entre quais dois valores? Esses valores são ________________. As\(z\) pontuações -são ________________, respectivamente.

    Resposta

    1. Cerca de 68% dos valores estão entre 166,02 e 178,7. As\(z\) pontuações -são —1 e 1.
    2. Cerca de 95% dos valores estão entre 159,68 e 185,04. As\(z\) pontuações -são —2 e 2.
    3. Cerca de 99,7% dos valores estão entre 153,34 e 191,38. As\(z\) pontuações -são —3 e 3.

    Exercício\(\PageIndex{6}\)

    As notas em um vestibular têm uma distribuição normal aproximada com média,\(\mu = 52\) pontos e desvio padrão,\(\sigma = 11\) pontos.

    1. Cerca de 68% dos\(y\) valores estão entre quais dois valores? Esses valores são ________________. As\(z\) pontuações -são ________________, respectivamente.
    2. Cerca de 95% dos\(y\) valores estão entre quais dois valores? Esses valores são ________________. As\(z\) pontuações -são ________________, respectivamente.
    3. Cerca de 99,7% dos\(y\) valores estão entre quais dois valores? Esses valores são ________________. As\(z\) pontuações -são ________________, respectivamente.
    Responda a

    Cerca de 68% dos valores estão entre os valores 41 e 63. As\(z\) pontuações -são —1 e 1, respectivamente.

    Resposta b

    Cerca de 95% dos valores estão entre os valores 30 e 74. As\(z\) pontuações -são —2 e 2, respectivamente.

    Resposta c

    Cerca de 99,7% dos valores estão entre os valores 19 e 85. As\(z\) pontuações -são —3 e 3, respectivamente.

    Resumo

    Um\(z\) -score é um valor padronizado. Sua distribuição é a pontuação\(Z \sim N(0,1)\). The mean of the \(z\)-scores is zero and the standard deviation is one. If \(y\) is the z normal padrão para um valor\(x\) from the normal distribution \(N(\mu, \sigma)\) then \(z\) tells you how many standard deviations \(x\) is above (greater than) or below (less than) \(\mu\).

    Revisão da fórmula

    \(Z \sim N(0, 1)\)

    \(z = a\)valor padronizado (\(z\)-score)

    média = 0; desvio padrão = 1

    Para encontrar o\(K\) décimo percentil de\(X\) quando as\(z\) pontuações -são conhecidas:

    \(k = \mu + (z)\sigma\)

    \(z\)-pontuação:\(z = \dfrac{x-\mu}{\sigma}\)

    \(Z =\)a variável aleatória para pontuações z

    \(Z \sim N(0, 1)\)

    Glossário

    Distribuição normal padrão
    uma variável aleatória contínua (RV)\(X \sim N(0, 1)\); quando\(X\) segue a distribuição normal padrão, geralmente é notada como\ (Z\ sim N (0, 1)\.
    \(z\)-pontuação
    a transformação linear da forma\(z = \dfrac{x-\mu}{\sigma}\); se essa transformação for aplicada a qualquer distribuição normal,\(X \sim N(\mu, \sigma\) o resultado será a distribuição normal padrão\(Z \sim N(0,1)\). Se essa transformação for aplicada a qualquer valor específico\(x\) do VD com média\(\mu\) e desvio padrão\(\sigma\), o resultado é chamado de\(z\) -score de\(x\). O\(z\) -score nos permite comparar dados que normalmente são distribuídos, mas escalados de forma diferente.

    Referências

    1. “Pressão arterial de homens e mulheres”. Stat Cruch, 2013. Disponível on-line em http://www.statcrunch.com/5.0/viewre...reportid=11960 (acessado em 14 de maio de 2013).
    2. “O uso de ferramentas epidemiológicas em populações afetadas por conflitos: recursos educacionais de acesso aberto para formuladores de políticas: cálculo de pontuações z”. Escola de Higiene e Medicina Tropical de Londres, 2009. Disponível on-line em http://conflict.lshtm.ac.uk/page_125.htm (acessado em 14 de maio de 2013).
    3. “Relatório de perfil total do grupo de idosos vinculados à faculdade de 2012.” Conselho Universitário, 2012. Disponível on-line em media.collegeboard.com/digita... Group-2012.pdf (acessado em 14 de maio de 2013).
    4. “Resumo das estatísticas educacionais: média da pontuação do ACT e desvios padrão por sexo e raça/etnia e porcentagem de participantes do teste ACT, por faixas de pontuação compostas selecionadas e campos de estudo planejados: anos selecionados, 1995 a 2009.” Centro Nacional de Estatísticas da Educação. Disponível on-line em nces.ed.gov/programs/digest/d... s/dt09_147.asp (acessado em 14 de maio de 2013).
    5. Dados do San Jose Mercury News.
    6. Dados do The World Almanac e do Book of Facts.
    7. “Lista de estádios por capacidade.” Wikipédia. Disponível on-line em en.wikipedia.org/wiki/List_o... ms_by_capacity (acessado em 14 de maio de 2013).
    8. Dados da National Basketball Association. Disponível on-line em www.nba.com (acessado em 14 de maio de 2013).