Skip to main content
Global

4.6: Distribuição hipergeométrica

  1. Last updated
  2. Save as PDF
  • Page ID
    189961

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    A distribuição hipergeométrica surge quando uma amostra de uma população finita, tornando os ensaios dependentes uns dos outros. Há cinco características de um experimento hipergeométrico.

    Características de um experimento hipergeométrico

    1. Você coleta amostras de dois grupos.
    2. Você está preocupado com um grupo de interesse, chamado primeiro grupo.
    3. Você coleta amostras sem substituição dos grupos combinados. Por exemplo, você quer escolher um time de softball de um grupo combinado de 11 homens e 13 mulheres. A equipe é composta por dez jogadores.
    4. Cada escolha não é independente, pois a amostragem não é substituída. No exemplo do softball, a probabilidade de escolher uma mulher primeiro é\(\frac{13}{24}\). A probabilidade de escolher um homem em segundo lugar é\(\frac{11}{23}\) se uma mulher for escolhida primeiro. É\(\frac{10}{23}\) se um homem fosse escolhido primeiro. A probabilidade da segunda escolha depende do que aconteceu na primeira escolha.
    5. Você não está lidando com os julgamentos de Bernoulli.

    Os resultados de um experimento hipergeométrico se ajustam a uma distribuição de probabilidade hipergeométrica. A variável aleatória\(X\) = o número de itens do grupo de interesse.

    Exemplo\(\PageIndex{1}\)

    Um prato de doces contém 100 jujubas e 80 gomas de goma. Cinquenta doces são colhidos aleatoriamente. Qual é a probabilidade de 35 dos 50 serem chicletes? Os dois grupos são jujubas e gomas. Como a pergunta probabilística pergunta sobre a probabilidade de colher chicletes, o grupo de interesse (primeiro grupo) é o gumdrops. O tamanho do grupo de interesse (primeiro grupo) é 80. O tamanho do segundo grupo é 100. O tamanho da amostra é 50 (jujubas ou gomas). Deixe\(X =\) o número de gomas na amostra ser 50. \(X\)assume os valores\(x = 0, 1, 2, ..., 50\). O que é a declaração de probabilidade escrita matematicamente?

    Responda

    \(P(x = 35)\)

    Exercício\(\PageIndex{1}\)

    Uma bolsa contém ladrilhos de letras. Quarenta e quatro dos blocos são vogais e 56 são consoantes. Sete peças são escolhidas aleatoriamente. Você quer saber a probabilidade de que quatro dos sete blocos sejam vogais. Qual é o grupo de interesse, o tamanho do grupo de interesse e o tamanho da amostra?

    Responda

    O grupo de interesse são os blocos das letras vocálicas. O tamanho do grupo de interesse é 44. O tamanho da amostra é sete.

    Exemplo\(\PageIndex{2}\)

    Suponha que uma remessa de 100 aparelhos de DVD tenha dez reprodutores defeituosos. Um inspetor escolhe aleatoriamente 12 para inspeção. Ele está interessado em determinar a probabilidade de que, entre os 12 jogadores, no máximo dois estejam com defeito. Os dois grupos são os 90 aparelhos de DVD sem defeito e os 10 aparelhos de DVD com defeito. O grupo de interesse (primeiro grupo) é o grupo defeituoso porque a pergunta probabilística pergunta sobre a probabilidade de no máximo dois aparelhos de DVD defeituosos. O tamanho da amostra é de 12 reprodutores de DVD. (Eles podem não estar com defeito ou com defeito.) Deixe\(X =\) o número de aparelhos de DVD com defeito na amostra de 12. \(X\)assume os valores\(0, 1, 2, \dotsc, 10\). \(X\)pode não assumir os valores 11 ou 12. O tamanho da amostra é 12, mas há apenas 10 reprodutores de DVD com defeito. Escreva a declaração de probabilidade matematicamente.

    Responda

    \(P(x \leq 2)\)

    Exercício\(\PageIndex{2}\)

    Um bruto de ovos contém 144 ovos. Sabe-se que uma massa bruta em particular tem 12 ovos rachados. Um inspetor escolhe aleatoriamente 15 para inspeção. Ela quer saber a probabilidade de que, entre os 15, no máximo três estejam quebrados. O que é\(X\) e quais valores ela assume?

    Responda

    Deixe\(X =\) o número de ovos rachados na amostra de 15. \(X\)assume os valores\(0, 1, 2, \dotsc, 12\).

    Exemplo\(\PageIndex{3}\)

    Você é presidente de uma organização de eventos especiais no campus. Você precisa de um comitê de sete estudantes para planejar uma festa de aniversário especial para o presidente da faculdade. Sua organização consiste em 18 mulheres e 15 homens. Você está interessado no número de homens em seu comitê. Se os membros do comitê forem selecionados aleatoriamente, qual é a probabilidade de seu comitê ter mais de quatro homens?

    Esse é um problema hipergeométrico porque você está escolhendo seu comitê entre dois grupos (homens e mulheres).

    1. Você está escolhendo com ou sem substituição?
    2. Qual é o grupo de interesse?
    3. Quantos estão no grupo de interesse?
    4. Quantos estão no outro grupo?
    5. Deixe\(X =\) _________ no comitê. Quais valores\(X\) assume?
    6. A questão da probabilidade é\(P(\) _______\()\).

    Solução

    1. sem
    2. os homens
    3. 15 homens
    4. 18 mulheres
    5. Deixe\(X =\) o número de homens no comitê. \(x = 0, 1, 2, \dotsc, 7\).
    6. \(P(x > 4)\)

    Exercício\(\PageIndex{3}\)

    Uma paleta tem 200 caixas de leite. Das 200 caixas, sabe-se que dez delas vazaram e não podem ser vendidas. Um corretor de ações escolhe aleatoriamente 18 para inspeção. Ele quer saber a probabilidade de que, entre os 18, não mais do que dois estejam vazando. Dê cinco razões pelas quais esse é um problema hipergeométrico.

    Responda
    • Existem dois grupos.
    • Você está preocupado com um grupo de interesse.
    • Você coleta amostras sem substituição.
    • Cada escolha não é independente.
    • Você não está lidando com os julgamentos de Bernoulli.

    Notação para o hipergeométrico:\(H =\) Hypergeometric Probability Distribution Function

    \[X \sim H(r, b, n)\]

    Leia isso como “\(X\)é uma variável aleatória com uma distribuição hipergeométrica”. Os parâmetros são\(r, b\), e\(n\);\(r =\) o tamanho do grupo de interesse (primeiro grupo),\(b =\) o tamanho do segundo grupo,\(n =\) o tamanho da amostra escolhida.

    Exemplo\(\PageIndex{4}\)

    Um comitê escolar deve ser escolhido aleatoriamente entre seis homens e cinco mulheres. Se o comitê consistir em quatro membros escolhidos aleatoriamente, qual é a probabilidade de dois deles serem homens? Quantos homens você espera que façam parte do comitê?

    Seja\(X\) = o número de homens no comitê de quatro. Os homens são o grupo de interesse (primeiro grupo).

    \(X\)assume os valores\(0, 1, 2, 3, 4\), onde\(r = 6, b = 5\),\(n = 4\) e. \(X \sim H(6, 5, 4)\)

    Encontre\(P(x = 2)\). \(P(x = 2) = 0.4545\)(calculadora ou computador)

    Atualmente, o TI-83+ e o TI-84 não têm funções de probabilidade hipergeométrica. Existem vários pacotes de computador, incluindo o Microsoft Excel, que funcionam.

    A probabilidade de haver dois homens no comitê é de cerca de 0,45.

    O gráfico de\(X \sim H(6, 5, 4)\) é:

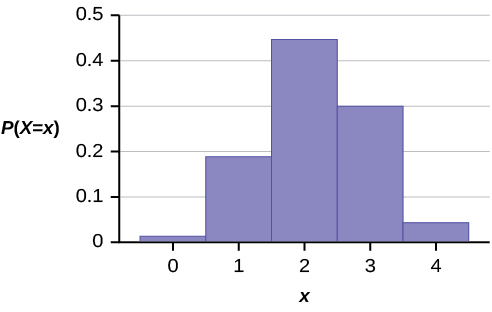
    Este gráfico mostra uma distribuição de probabilidade hipergeométrica. Tem cinco barras que são ligeiramente distribuídas normalmente. O eixo x mostra valores de 0 a 4 em incrementos de 1, representando o número de homens no comitê de quatro pessoas. O eixo y varia de 0 a 0,5 em incrementos de 0,1.
    Figura\(\PageIndex{1}\).

    O eixo y contém a probabilidade de\(X\), onde\(X =\) o número de homens no comitê.

    Você esperaria\(m = 2.18\) (cerca de dois) homens no comitê.

    A fórmula para a média é

    \[\mu = \frac{nr}{r+b} \frac{(4)(6)}{6+5} = 2.18\]

    Exercício\(\PageIndex{4}\)

    Um time de basquete interno deve ser escolhido aleatoriamente entre 15 meninos e 12 meninas. A equipe tem dez vagas. Você quer saber a probabilidade de oito dos jogadores serem meninos. Qual é o grupo de interesse e a amostra?

    Responda

    O grupo de interesse são os 15 meninos. A amostra consiste nas dez vagas do time de basquete interno.

    Resumo

    Um experimento hipergeométrico é um experimento estatístico com as seguintes propriedades:

    • Você coleta amostras de dois grupos.
    • Você está preocupado com um grupo de interesse, chamado primeiro grupo.
    • Você coleta amostras sem substituição dos grupos combinados.
    • Cada escolha não é independente, pois a amostragem não é substituída.
    • Você não está lidando com os julgamentos de Bernoulli.

    Os resultados de um experimento hipergeométrico se ajustam a uma distribuição de probabilidade hipergeométrica. A variável aleatória\(X\) = o número de itens do grupo de interesse. A distribuição de\(X\) é denotada\(X \sim H(r, b, n)\), onde\(r =\) o tamanho do grupo de interesse (primeiro grupo),\(b =\) o tamanho do segundo grupo e\(n =\) o tamanho da amostra escolhida. Daqui resulta isso\(n \leq r + b\). A média de\(X\) é\(\mu = \frac{nr}{r+b}\) e o desvio padrão é\(\sigma = \sqrt{\frac{rbn(r+b-n)}{(r+b)^{2}(r+b-1)}}\).

    Revisão da fórmula

    \(X \sim H(r, b, n)\)significa que a variável aleatória discreta\(X\) tem uma distribuição de probabilidade hipergeométrica com\(r =\) o tamanho do grupo de interesse (primeiro grupo),\(b =\) o tamanho do segundo grupo e\(n =\) o tamanho da amostra escolhida.

    \(X\)= o número de itens do grupo de interesse que estão na amostra escolhida e\(X\) podem assumir valores\(x = 0, 1, \dotsc,\) até o tamanho do grupo de interesse. (O valor mínimo para\(X\) pode ser maior que zero em alguns casos.)

    \(n \leq r + b\)

    A média de\(X\) é dada pela fórmula\(\mu = \frac{nr}{r+b}\) e o desvio padrão é\(= \sqrt{\frac{rbn(r+b-n)}{(r+b)^{2}(r+b-1)}}\).

    Use as informações a seguir para responder aos próximos cinco exercícios: Suponha que um grupo de estudantes de estatística seja dividido em dois grupos: cursos de negócios e cursos não comerciais. Existem 16 especializações de negócios no grupo e sete especializações não comerciais no grupo. Uma amostra aleatória de nove estudantes é coletada. Estamos interessados no número de empresas especializadas na amostra.

    Exercício\(\PageIndex{5}\)

    Em palavras, defina a variável aleatória\(X\).

    Responda

    \(X =\)o número de empresas especializadas em negócios na amostra.

    Exercício\(\PageIndex{6}\)

    \(X \sim\)_____ (_____, _____)

    Exercício\(\PageIndex{7}\)

    Quais valores\(X\) assume?

    Responda

    \(2, 3, 4, 5, 6, 7, 8, 9\)

    Exercício\(\PageIndex{8}\)

    Encontre o desvio padrão.

    Exercício\(\PageIndex{9}\)

    Em média (\(\mu\)), quantos você esperaria que fossem especialistas em negócios?

    Responda

    6.26

    Glossário

    Experiência hipergeométrica
    um experimento estatístico com as seguintes propriedades:
    1. Você coleta amostras de dois grupos.
    2. Você está preocupado com um grupo de interesse, chamado primeiro grupo.
    3. Você coleta amostras sem substituição dos grupos combinados.
    4. Cada escolha não é independente, pois a amostragem não é substituída.
    5. Você não está lidando com os julgamentos de Bernoulli.
    Probabilidade hipergeométrica
    uma variável aleatória discreta (RV) que é caracterizada por:
    1. Um número fixo de testes.
    2. A probabilidade de sucesso não é a mesma de uma tentativa para outra.
    Coletamos amostras de dois grupos de itens quando estamos interessados em apenas um grupo. \(X\)é definido como o número de sucessos do número total de itens escolhidos. Notação:\(X \sim H(r, b, n)\), onde é\(r =\) o número de itens no grupo de interesse,\(b =\) o número de itens no grupo que não são de interesse e\(n =\) o número de itens escolhidos.