Skip to main content
Global

4.5: Distribuição geométrica

  1. Last updated
  2. Save as PDF
  • Page ID
    189983

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Há três características principais de um experimento geométrico.

    1. Há um ou mais testes de Bernoulli com todos os fracassos, exceto o último, que é um sucesso. Em outras palavras, você continua repetindo o que está fazendo até o primeiro sucesso. Então você para. Por exemplo, você joga um dardo em um alvo até atingir o alvo. A primeira vez que você acerta o alvo é um “sucesso”, então você para de jogar o dardo. Pode levar seis tentativas até você atingir o alvo. Você pode pensar nas provações como fracasso, fracasso, fracasso, fracasso, sucesso, STOP.
    2. Em teoria, o número de testes poderia durar para sempre. Deve haver pelo menos um teste.
    3. A probabilidade,\(p\), de um sucesso e a probabilidade,\(q\), de um fracasso são as mesmas para cada tentativa. \(p + q = 1\)\(q = 1 − p\)e. Por exemplo, a probabilidade de rolar um três quando você lança um dado justo é\(\dfrac{1}{6}\). Isso é verdade, não importa quantas vezes você lance o dado. Suponha que você queira saber a probabilidade de obter os três primeiros no quinto rolo. Nos rolos de um a quatro, você não tem um rosto com três. A probabilidade de cada um dos rolos é\(q = \dfrac{5}{6}\) a probabilidade de uma falha. A probabilidade de conseguir um três na quinta jogada é\(\left(\dfrac{5}{6}\right)\left(\dfrac{5}{6}\right)\left(\dfrac{5}{6}\right)\left(\dfrac{5}{6}\right)\left(\dfrac{1}{6}\right) = 0.0804\).

    \(X =\)o número de ensaios independentes até o primeiro sucesso.

    Você joga um jogo de azar que pode ganhar ou perder (não há outras possibilidades) até perder. Sua probabilidade de perder é\(p = 0.57\). Qual é a probabilidade de levar cinco jogos até você perder? Deixe\(X =\) o número de jogos que você joga até perder (inclui o jogo perdedor). Em seguida,\(X\) assume os valores 1, 2, 3,... (poderia continuar indefinidamente). A questão da probabilidade é\(P(x = 5)\).

    Exemplo\(\PageIndex{1}\)

    Você joga um jogo de azar que pode ganhar ou perder (não há outras possibilidades) até perder. Sua probabilidade de perder é\(p = 0.57\). Qual é a probabilidade de levar cinco jogos até você perder? Deixe\(X =\) o número de jogos que você joga até perder (inclui o jogo perdedor). Em seguida,\(X\) assume os valores 1, 2, 3,... (poderia continuar indefinidamente). A questão da probabilidade é\(P(x = 5)\).

    Exercício\(\PageIndex{1}\)

    Você joga dardos em um tabuleiro até atingir a área central. Sua probabilidade de atingir a área central é\(p = 0.17\). Você quer descobrir a probabilidade de que sejam necessários oito arremessos até atingir o centro. Quais valores\(X\) assume?

    Responda

    \(1, 2, 3, 4, \dotsc, n\). Isso pode continuar indefinidamente.

    Exemplo\(\PageIndex{2}\)

    Uma engenheira de segurança acredita que 35% de todos os acidentes industriais em sua fábrica são causados pela falha dos funcionários em seguir as instruções. Ela decide examinar os relatórios de acidentes (selecionados aleatoriamente e substituídos na pilha após a leitura) até encontrar um que mostre um acidente causado pela falha dos funcionários em seguir as instruções. Em média, quantos relatórios a engenheira de segurança esperaria analisar até encontrar um relatório mostrando um acidente causado pela falha do funcionário em seguir as instruções? Qual é a probabilidade de a engenheira de segurança ter que examinar pelo menos três relatórios até encontrar um relatório mostrando um acidente causado pela falha do funcionário em seguir as instruções?

    Seja\(X\) = o número de acidentes que o engenheiro de segurança deve examinar até encontrar um relatório mostrando um acidente causado pela falha do funcionário em seguir as instruções. \(X\)assume os valores 1, 2, 3,... A primeira pergunta pede que você encontre o valor esperado ou a média. A segunda pergunta pede que você encontre\(P(x \geq 3)\). (“Pelo menos” se traduz em um símbolo “maior ou igual a”).

    Exercício\(\PageIndex{2}\)

    Um instrutor acha que 15% dos alunos obtêm menos de C no exame final. Ela decide examinar os exames finais (selecionados aleatoriamente e substituídos na pilha após a leitura) até encontrar um que mostre uma nota abaixo de C. Queremos saber a probabilidade de o instrutor ter que examinar pelo menos dez exames até encontrar um com uma nota abaixo de C. Qual é a pergunta de probabilidade declarado matematicamente?

    Responda

    \(P(x \leq 10)\)

    Exemplo\(\PageIndex{3}\)

    Suponha que você esteja procurando um estudante em sua faculdade que more a menos de cinco milhas de você. Você sabe que 55% dos 25.000 estudantes vivem a menos de cinco milhas de você. Você entra em contato aleatoriamente com estudantes da faculdade até que alguém diga que ele ou ela mora a menos de cinco milhas de você. Qual é a probabilidade de você precisar entrar em contato com quatro pessoas?

    Esse é um problema geométrico porque você pode ter várias falhas antes de ter o sucesso que deseja. Além disso, a probabilidade de sucesso permanece a mesma toda vez que você pergunta a um aluno se ele mora a menos de cinco milhas de você. Não há um número definido de testes (número de vezes que você pergunta a um aluno).

    1. Deixe\(X =\) o número de ____________ que você deve perguntar ____________ e diga que sim.
    2. Quais valores\(X\) assume?
    3. O que são\(p\) e\(q\)?
    4. A questão da probabilidade é\(P(\) _______\()\).

    Solução

    1. Deixe\(X =\) o número de alunos que você deve perguntar até que um diga sim.
    2. 1, 2, 3,..., (número total de estudantes)
    3. \(p = 0.55; q = 0.45\)
    4. \(P(x = 4)\)

    Exercício\(\PageIndex{3}\)

    Você precisa encontrar uma loja que tenha uma tinta de impressora especial. Você sabe que das lojas que vendem tinta para impressoras, 10% delas vendem a tinta especial. Você liga aleatoriamente para cada loja até que uma tenha a tinta necessária. O que são\(p\) e\(q\)?

    Responda

    \(p = 0.1\)

    \(q = 0.9\)

    Notação para o geométrico:\(G =\) Geometric Probability Distribution Function

    \(X \sim G(p)\)

    Leia isso como “\(X\)é uma variável aleatória com uma distribuição geométrica”. O parâmetro é\(p\);\(p =\) a probabilidade de sucesso de cada tentativa.

    Exemplo\(\PageIndex{4}\)

    Suponha que a probabilidade de um componente de computador com defeito seja 0,02. Os componentes são selecionados aleatoriamente. Determine a probabilidade de que o primeiro defeito seja causado pelo sétimo componente testado. Quantos componentes você espera testar até que um deles esteja com defeito?

    Seja\(X\) = o número de componentes do computador testados até que o primeiro defeito seja encontrado.

    \(X\)assume os valores 1, 2, 3,... onde\(p = 0.02\). \(X \sim G(0.02)\)

    Encontre\(P(x = 7)\). \(P(x = 7) = 0.0177\).

    Para descobrir a probabilidade de que\(x = 7\),

    • Digite 2 e D, DISTR
    • Role para baixo e selecione geometpdf (
    • Pressione ENTER
    • Digite 0,02, 7); pressione ENTER para ver o resultado:\(P(x = 7) = 0.0177\)

    Para encontrar a probabilidade de que\(x \leq 7\), siga as mesmas instruções, EXCETO, selecione E: geometcdf como a função de distribuição.

    A probabilidade de que o sétimo componente seja o primeiro defeito é 0,0177.

    O gráfico de\(X \sim G(0.02)\) é:

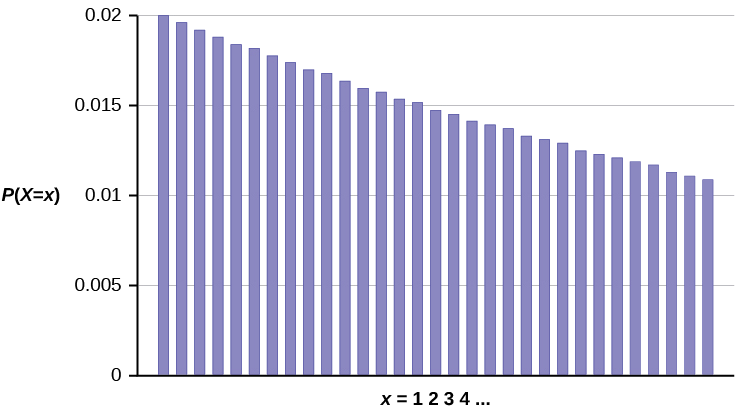
    Este gráfico mostra uma distribuição geométrica de probabilidade. Consiste em barras que atingem o pico à esquerda e se inclinam para baixo com cada barra sucessiva à direita. Os valores no eixo x contam o número de componentes do computador testados até que o defeito seja encontrado. O eixo y é escalado de 0 a 0,02 em incrementos de 0,005.
    Figura\(\PageIndex{1}\)

    O eixo y contém a probabilidade de\(x\), onde\(X =\) o número de componentes do computador testados.

    O número de componentes que você esperaria testar até encontrar o primeiro com defeito é a média,\(\mu = 50\).

    A fórmula para a média é

    \[\mu = \dfrac{1}{\text{p}} = \dfrac{1}{0.02} = 50\]

    A fórmula para a variância é

    \[\sigma^{2} = \left(\dfrac{1}{p}\right)\left(\dfrac{1}{p} - 1 \right) = \left(\dfrac{1}{0.02}\right)\left(\dfrac{1}{0.02} - 1 \right) = 2,450\]

    O desvio padrão é

    \[\sigma = \sqrt{\left(\dfrac{1}{p}\right)\left(\dfrac{1}{p} - 1\right)} = \sqrt{\left(\dfrac{1}{0.02}\right)\left(\dfrac{1}{0.02} - 1\right)} = 49.5\]

    Exercício\(\PageIndex{4}\)

    A probabilidade de uma haste de aço defeituosa é de 0,01. As barras de aço são selecionadas aleatoriamente. Determine a probabilidade de que o primeiro defeito ocorra na nona barra de aço. Use a calculadora TI-83+ ou TI-84 para encontrar a resposta.

    Responda

    \(P(x = 9) = 0.0092\)

    Exemplo\(\PageIndex{5}\)

    O risco vitalício de desenvolver câncer de pâncreas é de cerca de um em 78 (1,28%). Deixe\(X =\) o número de pessoas a quem você perguntar até que uma diga que tem câncer no pâncreas. Então\(X\) é uma variável aleatória discreta com uma distribuição geométrica:\(X \sim G\left(\dfrac{1}{78}\right)\) ou\(X \sim G(0.0128)\).

    1. Qual é a probabilidade de você perguntar a dez pessoas antes que uma diga que tem câncer no pâncreas?
    2. Qual é a probabilidade de você perguntar a 20 pessoas?
    3. Encontre a média (i) e (ii) o desvio padrão de\(X\).

    Responda

    1. \(P(x = 10) = \text{geometpdf}(0.0128, 10) = 0.0114\)
    2. \(P(x = 20) = \text{geometpdf}(0.0128, 20) = 0.01\)
      1. Significa\(= \mu = \dfrac{1}{p} = \dfrac{1}{0.0128} = 78\)
      2. Desvio padrão\(= \sigma = \sqrt{\dfrac{1-p}{p^{2}}} = \sqrt{\dfrac{1-0.0128}{0.0128^{2}}} \approx 77.6234\)

    Exercício\(\PageIndex{5}\)

    A taxa de alfabetização de uma nação mede a proporção de pessoas com 15 anos ou mais que sabem ler e escrever. A taxa de alfabetização das mulheres no Afeganistão é de 12%. Deixe\(X =\) o número de mulheres afegãs que você perguntar até que uma diga que ela é alfabetizada.

    1. Qual é a distribuição de probabilidade de\(X\)?
    2. Qual é a probabilidade de você perguntar a cinco mulheres antes que uma diga que é alfabetizada?
    3. Qual é a probabilidade de você perguntar a dez mulheres?
    4. Encontre a média (i) e (ii) o desvio padrão de\(X\).

    Responda

    1. \(X \sim G(0.12)\)
    2. \(P(x = 5) = \text{geometpdf}(0.12, 5) = 0.0720\)
    3. \(P(x = 10) = \text{geometpdf}(0.12, 10) = 0.0380\)
      1. Significa\(= \mu = \dfrac{1}{p} = \dfrac{1}{0.12} \approx 3333\)
      2. Desvio padrão\(= \sigma = \dfrac{1-p}{p^{2}} = \dfrac{1-0.12}{0.12^{2}} \approx 7.8174\)

    Referências

    1. “Millennials: um retrato da próxima geração”, Pew ResearchCenter. Disponível online em www.pewsocialtrends.org/files... -to-change.pdf (acessado em 15 de maio de 2013).
    2. “Millennials: Confiante. Conectado. Aberto à mudança.” Resumo executivo da PewResearch Social & Demographic Trends, 2013. Disponível on-line em http://www.pewsocialtrends.org/2010/...pen-to-change/ (acessado em 15 de maio de 2013).
    3. “Prevalência do HIV, total (% da população de 15 a 49 anos)”, Banco Mundial, 2013. Disponível on-line em http://data.worldbank.org/indicator/...last&sort=desc (acessado em 15 de maio de 2013).
    4. Pryor, John H., Linda DeAngelo, Laura Palucki Blake, Sylvia Hurtado, Serge Tran. The American Freshman: National Norms Fall 2011. Los Angeles: Programa de Pesquisa Institucional Cooperativa no Instituto de Pesquisa em Educação Superior da UCLA, 2011. Também disponível on-line em http://heri.ucla.edu/PDFs/pubs/TFS/N...eshman2011.pdf (acessado em 15 de maio de 2013).
    5. “Resumo da Avaliação Nacional de Risco e Vulnerabilidade 2007/8: Um perfil do Afeganistão”, A União Europeia e o ICON-Institute. Disponível online em ec.europa.eu/europeaid/where/... summary_en.pdf (acessado em 15 de maio de 2013).
    6. “The World FactBook”, Agência Central de Inteligência. Disponível on-line em https://www.cia.gov/library/publicat...k/geos/af.html (acessado em 15 de maio de 2013).
    7. “O UNICEF relata os Centros de Alfabetização Feminina no Afeganistão criados para ensinar às mulheres e meninas habilidades básicas de leitura [sic] e escrita”, disse a UNICEF Television. Vídeo disponível online em http://www.unicefusa.org/assets/vide...y-centers.html (acessado em 15 de maio de 2013).

    Revisão

    Há três características de um experimento geométrico:

    • Há um ou mais testes de Bernoulli com todos os fracassos, exceto o último, que é um sucesso.
    • Em teoria, o número de testes poderia durar para sempre. Deve haver pelo menos um teste.
    • A probabilidade,\(p\), de um sucesso e a probabilidade,\(q\), de um fracasso são as mesmas para cada tentativa.

    Em um experimento geométrico, defina a variável aleatória discreta\(X\) como o número de ensaios independentes até o primeiro sucesso. Dizemos que\(X\) tem uma distribuição geométrica e escrevemos\(X \sim G(p)\) onde\(p\) está a probabilidade de sucesso em uma única tentativa. A média da distribuição geométrica\(X \sim G(p)\) é\(\mu = \dfrac{1-p}{p^{2}} = \sqrt{\dfrac{1}{p}\left(\dfrac{1}{p} - 1\right)}\).

    Revisão da fórmula

    \(X \sim G(p)\)significa que a variável aleatória discreta\(X\) tem uma distribuição geométrica de probabilidade com probabilidade de sucesso em uma única tentativa\(p\).

    \(X =\)o número de ensaios independentes até o primeiro sucesso

    \(X\)assume os valores\(x = 1, 2, 3, \dotsc\)

    \(p =\)a probabilidade de sucesso em qualquer tentativa

    \(q =\)a probabilidade de uma falha em qualquer tentativa\(p + q = 1\)

    \(q = 1 – p\)

    A média é\(\mu = \dfrac{1}{p}\).

    O desvio padrão é\(\sigma = \dfrac{1-p}{p^{2}} = \sqrt{\dfrac{1}{p}\left(\dfrac{1}{p} - 1\right)}\).

    Use as seguintes informações para responder aos próximos seis exercícios: O Instituto de Pesquisa em Educação Superior da UCLA coletou dados de 203.967 calouros ingressantes pela primeira vez e em período integral de 270 faculdades e universidades de quatro anos nos EUA. 71,3% desses estudantes responderam que, sim, acreditam que casais do mesmo sexo devem ter direito ao estado civil legal. Suponha que você selecione aleatoriamente um calouro do estudo até encontrar um que responda “sim”. Você está interessado no número de calouros que você deve perguntar.

    Exercício 4.5.6

    Em palavras, defina a variável aleatória\(X\).

    Responda

    \(X =\)o número de calouros selecionados do estudo até que um respondeu “sim” que casais do mesmo sexo deveriam ter direito ao estado civil legal.

    Exercício 4.5.7

    \(X \sim\)_____ (_____, _____)

    Exercício 4.5.8

    Quais valores a variável aleatória\(X\) assume?

    Resposta

    1,2,...

    Exercício 4.5.9

    Construa a função de distribuição de probabilidade (PDF). Pare em\(x = 6\).

    \(x\) \(P(x)\)
    \ (x\) ">1 \ (P (x)\) ">
    \ (x\) ">2 \ (P (x)\) ">
    \ (x\) ">3 \ (P (x)\) ">
    \ (x\) ">4 \ (P (x)\) ">
    \ (x\) ">5 \ (P (x)\) ">
    \ (x\) ">6 \ (P (x)\) ">

    Exercício 4.5.10

    Em média (\(\mu\)), quantos calouros você esperaria ter que perguntar até encontrar um que respondesse “sim?”

    Resposta

    1.4

    Exercício 4.5.11

    Qual é a probabilidade de você precisar perguntar a menos de três calouros?

    Notas de pé

    1” Prevalência do HIV, total (% da população de 15 a 49 anos)”, Banco Mundial, 2013. Disponível on-line em http://data.worldbank.org/indicator/...pi_data_value - last&sort=desc (acessado em 15 de maio de 2013).

    Glossário

    Distribuição geométrica
    uma variável aleatória discreta (VR) que surge dos ensaios de Bernoulli; os ensaios são repetidos até o primeiro sucesso. A variável geométrica\(X\) é definida como o número de tentativas até o primeiro sucesso. Notação:\(X \sim G(p)\). A média é\(\mu = \dfrac{1}{p}\) e o desvio padrão é\(\sigma =\)

    \[\sqrt{\dfrac{1}{p}\left(\dfrac{1}{p} - 1\right)}\]

    . A probabilidade de\(x\) falhas exatas antes do primeiro sucesso é dada pela fórmula:\(P(X = x) = p(1 –p)^{x-1}\).
    Experiência geométrica
    um experimento estatístico com as seguintes propriedades:
    1. Há um ou mais testes de Bernoulli com todos os fracassos, exceto o último, que é um sucesso.
    2. Em teoria, o número de testes poderia durar para sempre. Deve haver pelo menos um teste.
    3. A probabilidade,\(p\), de um sucesso e a probabilidade,\(q\), de um fracasso não mudam de tentativa para tentativa.