4.4: Distribuição binomial

A distribuição binomial é frequentemente usada para modelar o número de sucessos em uma amostra de tamanho\(n\) extraída com a substituição de uma população de tamanho\(N\).

Três características de um experimento binomial

1. Há um número fixo de testes. Pense nas provações como repetições de um experimento. A letra\(n\) indica o número de ensaios.
2. Há apenas dois resultados possíveis, chamados de “sucesso” e “fracasso”, para cada tentativa. A letra\(p\) indica a probabilidade de sucesso em uma tentativa e\(q\) denota a probabilidade de falha em uma tentativa. \(p + q = 1\).
3. Os\(n\) ensaios são independentes e são repetidos usando condições idênticas. Como os\(n\) ensaios são independentes, o resultado de um ensaio não ajuda a prever o resultado de outro. Outra forma de dizer isso é que para cada tentativa individual, a probabilidade,\(p\), de um sucesso e a probabilidade,\(q\), de um fracasso permanecem as mesmas. Por exemplo, adivinhar aleatoriamente uma pergunta de estatística verdadeira e falsa tem apenas dois resultados. Se um sucesso é adivinhar corretamente, então uma falha é adivinhar incorretamente. Suponha que Joe sempre adivinhe corretamente qualquer pergunta estatística verdadeira-falsa com probabilidade\(p = 0.6\). Então,\(q = 0.4\). Isso significa que para cada pergunta estatística falsa e verdadeira que Joe responde, sua probabilidade de sucesso (\(p = 0.6\)) e sua probabilidade de falha (\(q = 0.4\)) permanecem as mesmas.

Os resultados de um experimento binomial se encaixam em uma distribuição de probabilidade binomial. A variável aleatória\(X =\) é o número de sucessos obtidos nos ensaios\(n\) independentes. A média,\(\mu\), e a variância,\(\sigma^{2}\), para a distribuição de probabilidade binomial são

\[\mu = np\]

e

\[\sigma^{2} = npq.\]

O desvio padrão,\(\sigma\), é então

\[\sigma = \sqrt{npq}.\]

Qualquer experimento que tenha as características dois e três e que\(n = 1\) seja chamado de Ensaio de Bernoulli (em homenagem a Jacob Bernoulli que, no final dos anos 1600, os estudou extensivamente). Um experimento binomial ocorre quando o número de sucessos é contado em um ou mais Ensaios de Bernoulli.

Exemplo\(\PageIndex{1}\)

No ABC College, a taxa de desistência de um curso de física elementar é de 30% para qualquer período. Isso implica que, em qualquer período, 70% dos alunos permanecem na classe durante todo o período. Um “sucesso” pode ser definido como um indivíduo que se retirou. A variável aleatória\(X =\) é o número de alunos que se retiram da aula de física elementar selecionada aleatoriamente.

Exercício\(\PageIndex{1}\)

O conselho estadual de saúde está preocupado com a quantidade de frutas disponível na merenda escolar. Quarenta e oito por cento das escolas do estado oferecem frutas em seus almoços todos os dias. Isso implica que 52% não o fazem. O que seria um “sucesso” nesse caso?

Responda

uma escola que oferece frutas em seu almoço todos os dias

Exemplo\(\PageIndex{2}\)

Suponha que você jogue um jogo que só pode ganhar ou perder. A probabilidade de você ganhar qualquer jogo é de 55% e a probabilidade de perder é de 45%. Cada jogo que você joga é independente. Se você jogar o jogo 20 vezes, escreva a função que descreve a probabilidade de você ganhar 15 das 20 vezes. Aqui, se você definir\(X\) como o número de vitórias,\(X\) assume os valores 0, 1, 2, 3,..., 20. A probabilidade de sucesso é\(p = 0.55\). A probabilidade de uma falha é\(q = 0.45\). O número de ensaios é\(n = 20\). A questão da probabilidade pode ser declarada matematicamente como\(P(x = 15)\).

Exercício\(\PageIndex{2}\)

Um treinador está ensinando um golfinho a fazer truques. A probabilidade de o golfinho realizar o truque com sucesso é de 35%, e a probabilidade de o golfinho não realizar o truque com sucesso é de 65%. De 20 tentativas, você quer descobrir a probabilidade de o golfinho ter sucesso 12 vezes. Indique a questão probabilística matematicamente.

Responda

\(P(x = 12)\)

Exemplo\(\PageIndex{3}\)

Uma moeda justa é lançada 15 vezes. Cada jogada é independente. Qual é a probabilidade de conseguir mais de dez cabeças? Deixe\(X =\) o número de cabeças em 15 voltas da moeda justa. \(X\)assume os valores 0, 1, 2, 3,..., 15. Como a moeda é justa,\(p = 0.5\)\(q = 0.5\) e. O número de ensaios é\(n = 15\). Indique a questão probabilística matematicamente.

Solução

\(P(x > 10)\)

Exercício\(\PageIndex{4}\)

Um dado justo de seis lados é lançado dez vezes. Cada rolo é independente. Você quer encontrar a probabilidade de rolar um mais de três vezes. Indique a questão probabilística matematicamente.

Responda

\(P(x > 3)\)

Exemplo\(\PageIndex{5}\)

Aproximadamente 70% dos estudantes de estatística fazem sua lição de casa a tempo de ser coletada e avaliada. Cada aluno faz a lição de casa de forma independente. Em uma aula de estatística de 50 alunos, qual é a probabilidade de que pelo menos 40 façam a lição de casa a tempo? Os alunos são selecionados aleatoriamente.

1. Esse é um problema binomial porque há apenas um sucesso ou um __________, há um número fixo de tentativas e a probabilidade de sucesso é de 0,70 para cada tentativa.
2. Se estivermos interessados no número de estudantes que fazem a lição de casa a tempo, como definimos\(X\)?
3. Quais valores\(x\) assume?
4. O que é um “fracasso”, em palavras?
5. Se\(p + q = 1\), então o que é\(q\)?
6. As palavras “pelo menos” são traduzidas como o tipo de desigualdade para a questão probabilística (\(P(x\)____\(40\)).

Solução

1. falha
2. \(X\)= o número de estudantes de estatística que fazem sua lição de casa a tempo
3. 0, 1, 2,..., 50
4. O fracasso é definido como um aluno que não conclui sua lição de casa a tempo. A probabilidade de sucesso é\(p = 0.70\). O número de ensaios é\(n = 50\).
5. \(q = 0.30\)
6. maior ou igual a (\(\geq\)). A questão da probabilidade é\(P(x \geq 40)\).

Exercício\(\PageIndex{5}\)

Sessenta e cinco por cento das pessoas passam no exame estadual de motorista na primeira tentativa. Um grupo de 50 pessoas que fizeram o exame de direção é selecionado aleatoriamente. Dê duas razões pelas quais esse é um problema binomial.

Responda

Esse é um problema binomial porque há apenas um sucesso ou um fracasso e há um número definido de tentativas. A probabilidade de sucesso permanece a mesma em cada tentativa.

Notação para o binômio:\(B =\) Binomial Probability Distribution Function

\[X \sim B(n, p)\]

Leia isso como “\(X\)é uma variável aleatória com uma distribuição binomial”. Os parâmetros são\(n\) e\(p\);\(n =\) número de ensaios,\(p =\) probabilidade de sucesso em cada tentativa.

Exemplo\(\PageIndex{6}\)

Foi afirmado que cerca de 41% dos trabalhadores adultos têm um diploma do ensino médio, mas não buscam nenhuma educação adicional. Se 20 trabalhadores adultos forem selecionados aleatoriamente, encontre a probabilidade de que no máximo 12 deles tenham um diploma do ensino médio, mas não busquem educação adicional. Quantos trabalhadores adultos você espera ter um diploma do ensino médio, mas não buscam nenhuma educação adicional?

Seja\(X\) = o número de trabalhadores que têm um diploma do ensino médio, mas não buscam nenhuma educação adicional.

\(X\)assume os valores 0, 1, 2,..., 20 onde\(n = 20, p = 0.41\),\(q = 1 – 0.41 = 0.59\) e. \(X \sim B(20, 0.41)\)

Encontre\(P(x \leq 12)\). \(P(x \leq 12) = 0.9738\). (calculadora ou computador)

Vá para 2 ^e DISTR. A sintaxe das instruções é a seguinte:

Para calcular (\(x = \text{value}): \text{binompdf}(n, p, \text{number}\)) se “número” for omitido, o resultado é a tabela de probabilidade binomial.

Para calcular\(P(x \leq \text{value}): \text{binomcdf}(n, p, \text{number})\) se o “número” é omitido, o resultado é a tabela de probabilidade binomial cumulativa.

Para este problema: Depois de estar na ^2ª DISTR, desça até binomcdf. Pressione ENTER. Digite 20,0.41,12). O resultado é\(P(x \leq 12) = 0.9738\).

Se você quiser encontrar\(P(x = 12)\), use o pdf (binompdf). Se você quiser encontrar\(P(x > 12)\), use\(1 - \text{binomcdf}(20,0.41,12)\).

A probabilidade de que no máximo 12 trabalhadores tenham um diploma do ensino médio, mas não busquem educação adicional, é de 0,9738.

O gráfico de\(X \sim B(20, 0.41)\) é o seguinte:

Figura\(\PageIndex{1}\): O gráfico de\(X \sim B(20, 0.41)\).

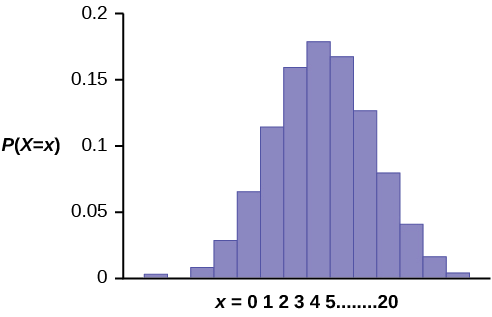
O eixo y contém a probabilidade de\(x\), where \(X =\) the number of workers who have only a high school diploma.

O número de trabalhadores adultos que você espera ter um diploma do ensino médio, mas não buscam nenhuma educação adicional, é a média,\(\mu = np = (20)(0.41) = 8.2\).

A fórmula para a variância é\(\sigma^{2} = npq\). O desvio padrão é\(\sigma = \sqrt{npq}\).

\[\sigma = \sqrt{(20)(0.41)(0.59)} = 2.20.\]

Exercício 4.4.5

Cerca de 32% dos estudantes participam de um programa comunitário de voluntariado fora da escola. Se 30 alunos forem selecionados aleatoriamente, encontre a probabilidade de que no máximo 14 deles participem de um programa comunitário de voluntariado fora da escola. Use a calculadora TI-83+ ou TI-84 para encontrar a resposta.

Responda

\(P(x \leq 14) = 0.9695\)

Exemplo\(\PageIndex{7}\)

No catálogo de materiais de arte da Jerry's Artarama de 2013, há 560 páginas. Oito das páginas apresentam artistas exclusivos. Suponha que tenhamos amostras aleatórias de 100 páginas. Deixe\(X =\) o número de páginas que apresentam artistas exclusivos.

1. Quais valores\(x\) assume?
2. O que é a distribuição de probabilidade? Encontre as seguintes probabilidades:
   1. a probabilidade de que duas páginas apresentem artistas exclusivos
   2. a probabilidade de que no máximo seis páginas apresentem artistas exclusivos
   3. a probabilidade de que mais de três páginas apresentem artistas exclusivos.
3. Usando as fórmulas, calcule a média (i) e o desvio padrão (ii).

Responda

1. \(x = 0, 1, 2, 3, 4, 5, 6, 7, 8\)
2. \(X \sim B(100,8560)(100,8560)\)
   1. \(P(x = 2) = \text{binompdf}\left(100,\dfrac{8}{560},2\right) = 0.2466\)
   2. \(P(x \leq 6) = \text{binomcdf}\left(100,\dfrac{8}{560},6\right) = 0.9994\)
   3. \(P(x > 3) = 1 – P(x \leq 3) = 1 – \text{binomcdf}\left(100,\dfrac{8}{560},3\right) = 1 – 0.9443 = 0.0557\)
3. 1. Significa\(= np = (100)\left(\dfrac{8}{560}\right) = \dfrac{800}{560} \approx 1.4286\)
   2. Desvio padrão\(= \sqrt{npq} = \sqrt{(100)\left(\dfrac{8}{560}\right)\left(\dfrac{552}{560}\right)} \approx 1.1867\)

Exercício\(\PageIndex{7}\)

De acordo com uma pesquisa da Gallup, 60% dos adultos americanos preferem economizar em vez de gastar. Seja\(X\) = o número de adultos americanos de uma amostra aleatória de 50 que preferem economizar em vez de gastar.

1. Para que serve a distribuição de probabilidade\(X\)?
2. Use sua calculadora para encontrar as seguintes probabilidades:
   1. a probabilidade de que 25 adultos da amostra prefiram economizar em vez de gastar
   2. a probabilidade de que no máximo 20 adultos prefiram economizar
   3. a probabilidade de que mais de 30 adultos prefiram economizar
3. Usando as fórmulas, calcule a média (i) e (ii) o desvio padrão de\(X\).

Responda

1. \(X \sim B(50, 0.6)\)
2. Usando a calculadora TI-83, 83+, 84 com as instruções fornecidas no Exemplo:
   1. \(P(x = 25) = \text{binompdf}(50, 0.6, 25) = 0.0405\)
   2. \(P(x \leq 20) = \text{binomcdf}(50, 0.6, 20) = 0.0034\)
   3. \((x > 30) = 1 - \text{binomcdf}(50, 0.6, 30) = 1 – 0.5535 = 0.4465\)
3. 1. Significa\(= np = 50(0.6) = 30\)
   2. Desvio padrão\(= \sqrt{npq} = \sqrt{50(0.6)(0.4)} \approx 3.4641\)

Exemplo\(\PageIndex{8}\)

O risco vitalício de desenvolver câncer de pâncreas é de cerca de um em 78 (1,28%). Suponha que amostremos aleatoriamente 200 pessoas. Seja\(X\) = o número de pessoas que desenvolverão câncer de pâncreas.

1. Para que serve a distribuição de probabilidade\(X\)?
2. Usando as fórmulas, calcule a média (i) e (ii) o desvio padrão de\(X\).
3. Use sua calculadora para descobrir a probabilidade de no máximo oito pessoas desenvolverem câncer de pâncreas
4. É mais provável que cinco ou seis pessoas desenvolvam câncer de pâncreas? Justifique sua resposta numericamente.

Responda

1. \(X \sim B(200, 0.0128)\)
2. 1. Significa\(= np = 200(0.0128) = 2.56\)
   2. Desvio padrão\(= \sqrt{npq} = \sqrt{(200)(0.0128)(0.9872)} \approx 1.5897\)
3. Usando a calculadora TI-83, 83+, 84 com as instruções fornecidas no Exemplo:
   \(P(x \leq 8) = \text{binomcdf}(200, 0.0128, 8) = 0.9988\)
4. \(P(x = 5) = \text{binompdf}(200, 0.0128, 5) = 0.0707\)
   \(P(x = 6) = \text{binompdf}(200, 0.0128, 6) = 0.0298\)
   Portanto\(P(x = 5) > P(x = 6)\), é mais provável que cinco pessoas desenvolvam câncer do que seis.

Exercício\(\PageIndex{8}\)

Durante a temporada regular da NBA de 2013, DeAndre Jordan, do Los Angeles Clippers, teve a maior taxa de conclusão de gols de campo da liga. DeAndre marcou com 61,3% de seus chutes. Suponha que você escolha uma amostra aleatória de 80 fotos feitas por DeAndre durante a temporada de 2013. Deixe\(X =\) o número de chutes que marcaram pontos.

1. Para que serve a distribuição de probabilidade\(X\)?
2. Usando as fórmulas, calcule a média (i) e (ii) o desvio padrão de\(X\).
3. Use sua calculadora para descobrir a probabilidade de DeAndre ter marcado com 60 desses tiros.
4. Descubra a probabilidade de DeAndre ter marcado com mais de 50 desses chutes.

Responda

1. \(X \sim B(80, 0.613)\)
2. 1. Significa\(= np = 80(0.613) = 49.04\)
   2. Desvio padrão\(= \sqrt{npq} = \sqrt{80(0.613)(0.387)} \approx 4.3564\)
3. Usando a calculadora TI-83, 83+, 84 com as instruções fornecidas no Exemplo:
   \(P(x = 60) = \text{binompdf}(80, 0.613, 60) = 0.0036\)
4. \(P(x > 50) = 1 – P(x \leq 50) = 1 – \text{binomcdf}(80, 0.613, 50) = 1 – 0.6282 = 0.3718\)

Exemplo\(\PageIndex{9}\)

O exemplo a seguir ilustra um problema que não é binomial. Isso viola a condição de independência. O ABC College tem um comitê consultivo estudantil composto por dez funcionários e seis estudantes. O comitê deseja escolher um presidente e um gravador. Qual é a probabilidade de que o presidente e o gravador sejam ambos estudantes? Os nomes de todos os membros do comitê são colocados em uma caixa e dois nomes são sorteados sem substituição. O primeiro nome sorteado determina o presidente e o segundo nome o gravador. Existem dois testes. No entanto, os ensaios não são independentes porque o resultado do primeiro ensaio afeta o resultado do segundo ensaio. A probabilidade de um aluno no primeiro sorteio é\(\dfrac{6}{16}\). A probabilidade de um aluno no segundo sorteio é\(\dfrac{5}{15}\) quando o primeiro sorteio seleciona um aluno. A probabilidade é\(\dfrac{6}{15}\), quando o primeiro sorteio seleciona um membro da equipe. A probabilidade de desenhar o nome de um aluno muda em cada um dos julgamentos e, portanto, viola a condição de independência.

Exercício\(\PageIndex{9}\)

Uma equipe de lacrosse está selecionando um capitão. Os nomes de todos os idosos são colocados em um chapéu, e os três primeiros sorteados serão os capitães. Os nomes não são substituídos depois de sorteados (uma pessoa não pode ser dois capitães). Você quer ver se todos os capitães jogam na mesma posição. Declare se isso é binomial ou não e indique o porquê.

Responda

Isso não é binomial porque os nomes não são substituídos, o que significa que a probabilidade muda a cada vez que um nome é sorteado. Isso viola a condição de independência.

Referências

1. “Acesso à eletricidade (% da população)”, Banco Mundial, 2013. Disponível on-line em http://data.worldbank.org/indicator/...first&sort=asc (acessado em 15 de maio de 2015).
2. “Educação a distância”. Wikipédia. Disponível on-line em http://en.Wikipedia.org/wiki/Distance_education (acessado em 15 de maio de 2013).
3. “Estatísticas da NBA — 2013”, ESPN NBA, 2013. Disponível on-line em http://espn.go.com/nba/statistics/_/seasontype/2 (acessado em 15 de maio de 2013).
4. Newport, Frank. “Os americanos ainda gostam de economizar em vez de gastar: poucas diferenças demográficas observadas nessas visões além da renda”, GALLUP® Economy, 2013. Disponível on-line em http://www.gallup.com/poll/162368/am... -spending.aspx (acessado em 15 de maio de 2013).
5. Pryor, John H., Linda DeAngelo, Laura Palucki Blake, Sylvia Hurtado, Serge Tran. The American Freshman: National Norms Fall 2011. Los Angeles: Programa de Pesquisa Institucional Cooperativa no Instituto de Pesquisa em Educação Superior da UCLA, 2011. Também disponível on-line em http://heri.ucla.edu/PDFs/pubs/TFS/N...eshman2011.pdf (acessado em 15 de maio de 2013).
6. “The World FactBook”, Agência Central de Inteligência. Disponível on-line em https://www.cia.gov/library/publicat...k/geos/af.html (acessado em 15 de maio de 2013).
7. “Quais são as principais estatísticas sobre o câncer de pâncreas?” Sociedade Americana do Câncer, 2013. Disponível on-line em www.cancer.org/cancer/pancrea... key-statistics (acessado em 15 de maio de 2013).

Revisão

Um experimento estatístico pode ser classificado como um experimento binomial se as seguintes condições forem atendidas:

Há um número fixo de ensaios,\(n\).

Existem apenas dois resultados possíveis, chamados de “sucesso” e “fracasso” para cada tentativa. A letra\(p\) indica a probabilidade de sucesso em uma tentativa e\(q\) denota a probabilidade de falha em uma tentativa.

Os\(n\) ensaios são independentes e são repetidos usando condições idênticas.

Os resultados de um experimento binomial se encaixam em uma distribuição de probabilidade binomial. A variável aleatória\(X =\) é o número de sucessos obtidos nos ensaios\(n\) independentes. A média de\(X\) pode ser calculada usando a fórmula\(\mu = np\), e o desvio padrão é dado pela fórmula\(\sigma = \sqrt{npq}\).

Revisão da fórmula

• \(X \sim B(n, p)\)significa que a variável aleatória discreta\(X\) tem uma distribuição de probabilidade binomial com\(n\) tentativas e probabilidade de sucesso\(p\).
• \(X =\)o número de sucessos em ensaios\(n\) independentes
• \(n =\)o número de ensaios independentes
• \(X\)assume os valores\(x = 0, 1, 2, 3, \dotsc, n\)
• \(p =\)a probabilidade de sucesso em qualquer tentativa
• \(q =\)a probabilidade de uma falha em qualquer tentativa
• \(p + q = 1\)
• \(q = 1 – p\)

A média de\(X\) é\(\mu = np\). O desvio padrão de\(X\) é\(\sigma = \sqrt{npq}\).

Use as seguintes informações para responder aos próximos oito exercícios: O Instituto de Pesquisa em Educação Superior da UCLA coletou dados de 203.967 calouros ingressantes pela primeira vez e em período integral de 270 faculdades e universidades de quatro anos nos EUA. 71,3% desses estudantes responderam que, sim, acreditam que casais do mesmo sexo devem ter direito ao estado civil legal. Suponha que você escolha aleatoriamente oito calouros pela primeira vez e em período integral da pesquisa. Você está interessado no número que acredita que casais do mesmo sexo devem ter direito ao estado civil legal.

Exercício 4.4.9

Em palavras, defina a variável aleatória\(X\).

Responda

\(X =\)o número que responde “sim”

Exercício 4.4.10

\(X \sim\)_____ (_____, _____)

Exercício 4.4.11

Quais valores a variável aleatória\(X\) assume?

Responda

0, 1, 2, 3, 4, 5, 6, 7, 8

Exercício 4.4.12

Construa a função de distribuição de probabilidade (PDF).

\(x\)	\(P(x)\)

Exercício 4.4.13

Em média (\(\mu\)), quantos você esperaria que respondessem sim?

Responda

5.7

Exercício 4.4.14

O que é o desvio padrão (\(\sigma\))?

Exercício 4.4.15

Qual é a probabilidade de que no máximo cinco dos calouros respondam “sim”?

Responda

0,4151

Exercício 4.4.16

Qual é a probabilidade de pelo menos dois dos calouros responderem “sim”?

Glossário

Experimento binomial

um experimento estatístico que satisfaz as três condições a seguir:

1. Há um número fixo de ensaios,\(n\).
2. Há apenas dois resultados possíveis, chamados de “sucesso” e “fracasso”, para cada tentativa. A letra\(p\) indica a probabilidade de sucesso em uma tentativa e\(q\) denota a probabilidade de falha em uma tentativa.
3. Os\(n\) ensaios são independentes e são repetidos usando condições idênticas.

Testes de Bernoulli

um experimento com as seguintes características:

1. Há apenas dois resultados possíveis chamados de “sucesso” e “fracasso” para cada tentativa.
2. A probabilidade\(p\) de sucesso é a mesma para qualquer tentativa (portanto, a probabilidade\(q = 1 − p\) de falha é a mesma para qualquer tentativa).

Distribuição de probabilidade binomial

uma variável aleatória discreta (VR) que surge dos ensaios de Bernoulli; há um número fixo,\(n\), de ensaios independentes. “Independente” significa que o resultado de qualquer ensaio (por exemplo, o primeiro ensaio) não afeta os resultados dos ensaios a seguir, e todos os ensaios são conduzidos nas mesmas condições. Nessas circunstâncias, o binômio RV\(X\) é definido como o número de sucessos em\(n\) ensaios. A notação é:\(X ~ B(n, p)\). A média é\(\mu = np\) e o desvio padrão é\(\sigma = \sqrt{npq}\). A probabilidade exata de\(x\) sucesso nos\(n\) testes é
\(P(X = x) = {n \choose x}p^{x}q^{n-x}\).