Skip to main content
Global

3.6: Diagramas de Árvore e Venn

  1. Last updated
  2. Save as PDF
  • Page ID
    190049

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Às vezes, quando os problemas de probabilidade são complexos, pode ser útil representar graficamente a situação. Diagramas de árvores e diagramas de Venn são duas ferramentas que podem ser usadas para visualizar e resolver probabilidades condicionais.

    Diagramas de árvores

    Um diagrama de árvore é um tipo especial de gráfico usado para determinar os resultados de um experimento. Consiste em “ramificações” rotuladas com frequências ou probabilidades. Os diagramas de árvore podem facilitar a visualização e a resolução de alguns problemas de probabilidade. O exemplo a seguir ilustra como usar um diagrama de árvore.

    Exemplo\(\PageIndex{1}\): Probabilities from Sampling with replacement

    Em uma urna, há 11 bolas. Três bolas são vermelhas (\(\text{R}\)) e oito bolas são azuis (\(\text{B}\)). Desenhe duas bolas, uma de cada vez, com a substituição (lembre-se de que “com substituição” significa que você coloca a primeira bola de volta na urna antes de selecionar a segunda bola). O diagrama em árvore usando frequências que mostram todos os resultados possíveis segue.

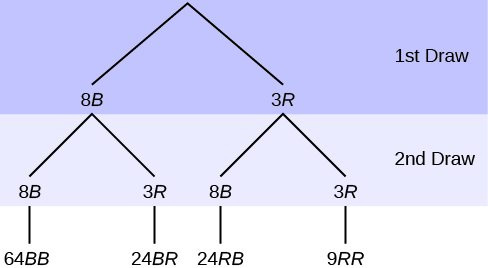
    Figura\(\PageIndex{1}\): Total = 64 + 24 + 24 + 9 = 121

    O primeiro conjunto de galhos representa o primeiro sorteio. O segundo conjunto de ramificações representa o segundo sorteio. Cada um dos resultados é distinto. Na verdade, podemos listar cada bola vermelha como R 1, R 2 e R 3 e cada bola azul como B 1, B 2, B 3, B 4, B 5, B 6, B 7 e B 8. Em seguida, os nove resultados RR podem ser escritos como:

    R 1 R 1 R 1 R 2 R 1 R 3 R 2 R 1 R 2 R 2 R 2 R 3 R 3 R 1 R 3 R 2 R 3 R 3

    Os outros resultados são semelhantes.

    Há um total de 11 bolas na urna. Desenhe duas bolas, uma de cada vez, com a substituição. Existem 11 (11) = 121 resultados, o tamanho do espaço amostral.

    Exercício\(\PageIndex{1}\)

    Em um baralho padrão, existem 52 cartas. 12 cartas são cartas com face (evento\(\text{F}\)) e 40 cartas não são cartas com face (evento\(\text{N}\)). Compre duas cartas, uma de cada vez, com a substituição. Todos os resultados possíveis são mostrados no diagrama da árvore como frequências. Usando o diagrama de árvore, calcule\(P(\text{FF})\).

    Figura\(\PageIndex{2}\):

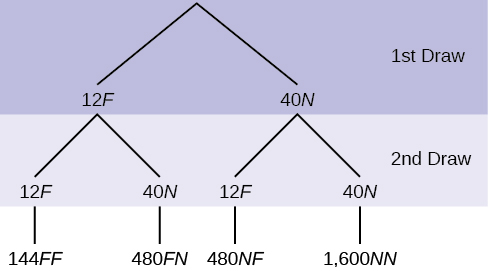
    Resposta

    O número total de resultados é 144 + 480 + 480 + 1600 = 2.704.

    \[P(\text{FF}) = \frac{144}{144+480+480+1,600} = \frac{144}{2,704} = \frac{9}{169}\]

    1. a. Liste os 24 resultados do BR: B 1 R 1, B 1 R 2, B 1 R 3,...
    2. b. Usando o diagrama de árvore, calcule P (RR).
    3. c. Usando o diagrama de árvore, calcule\(P(\text{RB OR BR})\).
    4. d. Usando o diagrama de árvore, calcule\(P(\text{R on 1st draw AND B on 2nd draw})\).
    5. e. Usando o diagrama da árvore, calcule P (R no 2º sorteio DADO B no 1º sorteio).
    6. Usando o diagrama de árvore, calcule\(P(\text{BB})\).
    7. g. Usando o diagrama de árvore, calcule\(P(\text{B on the 2nd draw given R on the first draw})\).

    Solução

    1. B 1 R 1; B 1 R 2; B 1 R 3; B 2 R 1; B 2 R 2; B 2 R 3; B 3 R 1; B 3 R 2; B 3 R 3; B 4 R 1; B 4 R 2; B 4 R 3; B 5 R 1; B 5 R 2; B 5 R 3; B 6 R 1; B 6 R 2; B 6 R 3 B 7 R 1; B 7 R 2; B 7 R 3; B 8 R 1; B 8 R 2; B 8 R 3
    2. \(P(\text{RR}) = \left(\frac{3}{11}\right) \left(\frac{3}{11}\right) = \frac{9}{121}\)
    3. \(P(\text{RB OR BR}) = \left(\frac{3}{11}\right) \left(\frac{8}{11}\right) + \left(\frac{8}{11}\right) \left(\frac{3}{11}\right) = \frac{48}{121}\)
    4. \(P(\text{R on 1st draw AND B on 2nd draw}) = P(\text{RB}) = \left(\frac{3}{11}\right) \left(\frac{8}{11}\right) = \frac{24}{121}\)
    5. P (R no 2º sorteio DADO B no 1º sorteio) = P (R no 2º sorteio | B no 1º)\(\frac{24}{88}\) = =\(\frac{3}{11}\) Este problema é condicional. O espaço amostral foi reduzido para aqueles resultados que já têm um azul no primeiro sorteio. Existem 24 + 64 = 88 resultados possíveis (24 BR e 64 BB). Vinte e quatro dos 88 resultados possíveis são BR. \(\frac{24}{88}\)=\(\frac{3}{11}\)
    6. \(P(\text{BB}) = \frac{64}{121}\)
    7. \(P(\text{B on 2nd draw|R on 1st draw}) = \frac{8}{11}\). Existem 9 + 24 resultados\(\text{R}\) no primeiro sorteio (9 RR e 24 RB). O espaço amostral é então 9 + 24 = 33. 24 dos 33 resultados têm\(\text{B}\) no segundo sorteio. A probabilidade é então\(\frac{24}{33}\).

    Exemplo\(\PageIndex{2}\): Probabilities from Sampling without replacement

    Uma urna tem três bolinhas vermelhas e oito bolas azuis nela. Tire duas bolinhas, uma de cada vez, desta vez sem reposição, da urna. (lembre-se de que “sem substituição” significa que você não coloca a primeira bola de volta antes de selecionar a segunda bola de gude). A seguir está um diagrama de árvore para essa situação. As ramificações são rotuladas com probabilidades em vez de frequências. Os números nas extremidades das ramificações são calculados multiplicando-se os números nas duas ramificações correspondentes, por exemplo,\(\left(\frac{3}{11}\right)\left(\frac{2}{10}\right) = \frac{6}{110}\).

    Figura\(\PageIndex{3}\): Total\(= \frac{56+24+24+6}{110} = \frac{110}{110} = 1\)

    Se você tirar um vermelho no primeiro sorteio das três possibilidades vermelhas, restam duas bolinhas vermelhas para desenhar no segundo sorteio. Você não coloca ou substitui a primeira bola de gude depois de desenhá-la. Você desenha sem reposição, de modo que no segundo sorteio restam dez bolinhas na urna.

    Calcule as seguintes probabilidades usando o diagrama de árvore.

    1. \(P(\text{RR}) =\)________
    2. Preencha os espaços em branco:\(P(\text{RB OR BR}) = \left(\frac{3}{11}\right) \left(\frac{8}{10}\right) +\) (___) (___)\(= \frac{48}{110}\)
    3. \(P(\text{R on 2nd|B on 1st}) =\)
    4. Preencha os espaços em branco:\(P(\text{R on 1st AND B on 2nd}) = P(\text{RB}) =\) (___) (___)\(= \frac{24}{110}\)
    5. Encontre\(P(\text{BB})\).
    6. Encontre\(P(\text{B on 2nd|R on 1st})\).

    Respostas

    1. \(P(\text{RR}) = \left(\frac{3}{11}\right)\left(\frac{2}{10}\right) = \frac{6}{110}\)
    2. \(P(\text{RB OR BR}) = \left(\frac{3}{11}\right)\left(\frac{8}{10}\right) + \left(\frac{8}{11}\right)\left(\frac{3}{10}\right) = \frac{48}{110}\)
    3. \(P(\text{R on 2nd|B on 1st}) = \frac{3}{10}\)
    4. \(P(\text{R on 1st AND B on 2nd}) = P(\text{RB}) = \left(\frac{3}{11}\right) \left(\frac{8}{10}\right) = \frac{24}{110}\)
    5. \(P(\text{BB}) = \left(\frac{8}{11}\right)\left(\frac{7}{10}\right)\)
    6. Usando o diagrama de árvore,\(P(\text{B on 2nd|R on 1st}) = P(\text{R|B}) = \frac{8}{10}\).

    Se estivermos usando probabilidades, podemos rotular a árvore da seguinte maneira geral.

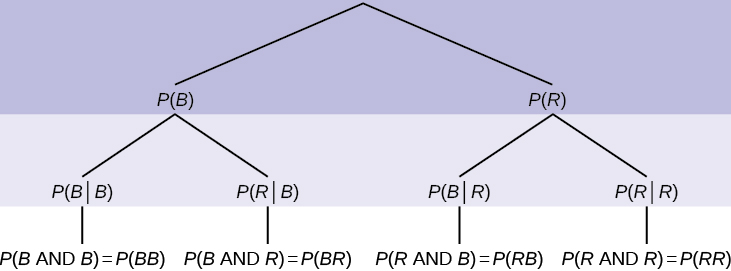
    • \(P(\text{R|R})\)aqui significa\(P(\text{R on 2nd|R on 1st})\)
    • \(P(\text{B|R})\)aqui significa\(P(\text{B on 2nd|R on 1st})\)
    • \(P(\text{R|B})\)aqui significa\(P(\text{R on 2nd|B on 1st})\)
    • \(P(\text{B|B})\)aqui significa\(P(\text{B on 2nd|B on 1st})\)

    Exercício\(\PageIndex{2}\)

    Em um baralho padrão, existem 52 cartas. Doze cartas são cartas com face (\(\text{F}\)) e 40 cartas não são cartas com face (\(\text{N}\)). Compre duas cartas, uma de cada vez, sem substituí-las. O diagrama da árvore é rotulado com todas as probabilidades possíveis.

    Figura\(\PageIndex{4}\):
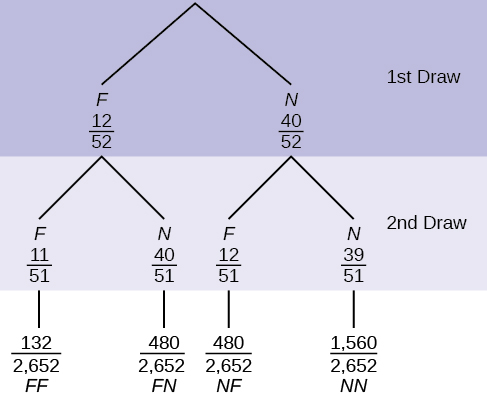
    1. Encontre\(P(\text{FN OR NF})\).
    2. Encontre\(P(\text{N|F})\).
    3. Encontre\(P(\text{at most one face card})\).
      Dica: “No máximo uma carta com face” significa zero ou uma carta com face.
    4. Encontre\(P(\text{at least on face card})\).
      Dica: “Pelo menos uma carta com face” significa uma ou duas cartas com face.

    Resposta

    1. \(P(\text{FN OR NF}) = \frac{480}{2,652} + \frac{480}{2,652} = \frac{960}{2,652} = \frac{80}{221}\)
    2. \(P(\text{N|F}) = \frac{40}{51}\)
    3. \(P(\text{at most one face card}) = \frac{(480+480+1,560)}{2,652} = \frac{2,520}{2,652}\)
    4. \(P(\text{at least one face card}) = \frac{(132+480+480)}{2,652} = \frac{1,092}{2,652}\)

    Exemplo\(\PageIndex{3}\)

    Uma ninhada de gatinhos disponível para adoção na Humane Society tem quatro gatinhos malhados e cinco gatinhos pretos. Uma família chega e seleciona aleatoriamente dois gatinhos (sem substituto) para adoção.

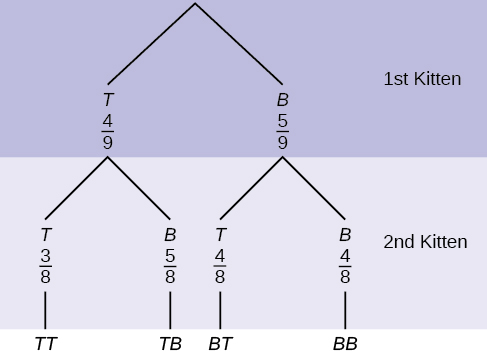
    1. Qual é a probabilidade de os dois gatinhos serem malhados?
      a.\(\left(\frac{1}{2}\right) \left(\frac{1}{2}\right)\) b.\(\left(\frac{4}{9}\right) \left(\frac{4}{9}\right)\) c.\(\left(\frac{4}{9}\right) \left(\frac{3}{8}\right)\) d.\(\left(\frac{4}{9}\right) \left(\frac{5}{9}\right)\)
    2. Qual é a probabilidade de um gatinho de cada cor ser selecionado?
      a.\(\left(\frac{4}{9}\right) \left(\frac{5}{9}\right)\) b.\(\left(\frac{4}{9}\right) \left(\frac{5}{8}\right)\) c.\(\left(\frac{4}{9}\right) \left(\frac{5}{9}\right)\) +\(\left(\frac{5}{9}\right) \left(\frac{4}{9}\right)\) d.\(\left(\frac{4}{9}\right) \left(\frac{5}{8}\right)\) +\(\left(\frac{5}{9}\right) \left(\frac{4}{8}\right)\)
    3. Qual é a probabilidade de um gato malhado ser escolhido como o segundo gatinho quando um gatinho preto foi escolhido como o primeiro?
    4. Qual a probabilidade de escolher dois gatinhos da mesma cor?

    Resposta

    a. c, b. d, c.\(\frac{4}{8}\), d.\(\frac{32}{72}\)

    Exercício\(\PageIndex{3}\)

    Suponha que haja quatro bolas vermelhas e três bolas amarelas em uma caixa. Três bolas são retiradas da caixa sem substituição. Qual é a probabilidade de que uma bola de cada cor seja selecionada?

    Resposta

    \(\left(\frac{4}{7}\right) \left(\frac{3}{6}\right)\)+\(\left(\frac{3}{7}\right) \left(\frac{4}{6}\right)\)

    Diagrama de Venn

    Um diagrama de Venn é uma imagem que representa os resultados de um experimento. Geralmente consiste em uma caixa que representa o espaço amostral S junto com círculos ou ovais. Os círculos ou ovais representam eventos.

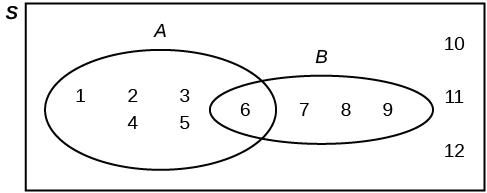
    Exemplo\(\PageIndex{4}\)

    Suponha que um experimento tenha os resultados 1, 2, 3,..., 12 em que cada resultado tenha uma chance igual de ocorrer. Deixe o evento\(\text{A} =\) {1, 2, 3, 4, 5, 6} e o evento\(\text{B} =\) {6, 7, 8, 9}. Em seguida,\(\text{A AND B} =\) {6} e\(\text{A OR B} =\) {1, 2, 3, 4, 5, 6, 7, 8, 9}. O diagrama de Venn é o seguinte:

    Figura\(\PageIndex{5}\):

    Exercício\(\PageIndex{4}\)

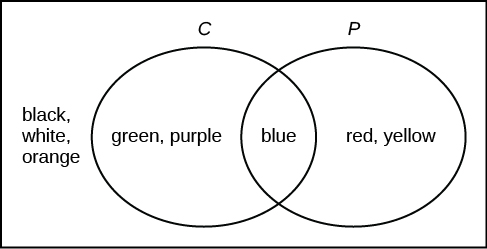
    Suponha que um experimento tenha resultados em preto, branco, vermelho, laranja, amarelo, verde, azul e roxo, onde cada resultado tem a mesma chance de ocorrer. Seja o evento\(\text{C} =\) {verde, azul, roxo} e o evento\(\text{P} =\) {vermelho, amarelo, azul}. Depois\(\text{C AND P} =\) {azul} e\(\text{C OR P} =\) {verde, azul, roxo, vermelho, amarelo}. Desenhe um diagrama de Venn representando essa situação.

    Responda

    Figura\(\PageIndex{6}\):

    Exemplo\(\PageIndex{5}\)

    Jogue duas moedas justas. Deixe\(\text{A} =\) as pontas na primeira moeda. Deixe\(\text{B} =\) as pontas na segunda moeda. Em seguida,\(\text{A} =\) {TT, TH} e\(\text{B} =\) {TT, HT}. Portanto,\(\text{A AND B} =\) {TT}. \(\text{A OR B} =\){TH, TT, HT}.

    O espaço da amostra quando você joga duas moedas justas é\(X =\) {HH, HT, TH, TT}. O resultado é o HH\(\text{NEITHER A NOR B}\). O diagrama de Venn é o seguinte:

    Figura\(\PageIndex{7}\):

    Exercício\(\PageIndex{5}\)

    Lance um dado justo de seis lados. Deixe\(\text{A} =\) um número primo de pontos ser lançado. Deixe rolar\(\text{B} =\) um número ímpar de pontos. Em seguida,\(\text{A} =\) {2, 3, 5} e\(\text{B} =\) {1, 3, 5}. Portanto,\(\text{A AND B} =\) {3, 5}. \(\text{A OR B} =\){1, 2, 3, 5}. O espaço amostral para rolar um dado justo é\(\text{S} =\) {1, 2, 3, 4, 5, 6}. Desenhe um diagrama de Venn representando essa situação.

    Responda

    Exemplo\(\PageIndex{6}\): Probability and Venn Diagrams

    Quarenta por cento dos estudantes de uma faculdade local pertencem a um clube e 50% trabalham em tempo parcial. Cinco por cento dos estudantes trabalham a tempo parcial e pertencem a um clube. Desenhe um diagrama de Venn mostrando os relacionamentos. Deixe o\(\text{C} =\) aluno pertencer a um clube e o\(\text{PT} =\) aluno trabalhar a tempo parcial.

    Figura\(\PageIndex{8}\):

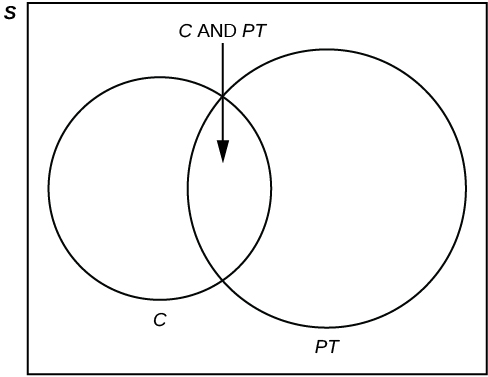
    Se um aluno for selecionado aleatoriamente, encontre

    • a probabilidade de o aluno pertencer a um clube. \(P(\text{C}) = 0.40\)
    • a probabilidade de o aluno trabalhar a tempo parcial. \(P(\text{PT}) = 0.50\)
    • a probabilidade de o aluno pertencer a um clube E trabalhar a tempo parcial. \(P(\text{C AND PT}) = 0.05\)
    • a probabilidade de o aluno pertencer a um clube, uma vez que o aluno trabalha a tempo parcial. \(P(\text{C|PT}) = \frac{P(\text{C AND PT})}{P(\text{PT})} = \frac{0.05}{0.50} = 0.1\)
    • a probabilidade de o aluno pertencer a um clube OU trabalhar a tempo parcial. \(P(\text{C OR PT}) = P(\text{C}) + P(\text{PT}) - P(\text{C AND PT}) = 0.40 + 0.50 - 0.05 = 0.85\)

    Exercício\(\PageIndex{6}\)

    Cinquenta por cento dos trabalhadores de uma fábrica trabalham em um segundo emprego, 25% têm um cônjuge que também trabalha, 5% trabalham em um segundo emprego e têm um cônjuge que também trabalha. Desenhe um diagrama de Venn mostrando os relacionamentos. Deixe\(\text{W} =\) trabalhar em um segundo emprego e o\(\text{S} =\) cônjuge também trabalha.

    Responda

    Figura\(\PageIndex{9}\):

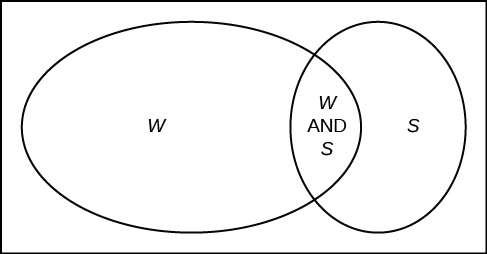
    Exemplo\(\PageIndex{7}\)

    Uma pessoa com sangue tipo O e fator Rh negativo (Rh-) pode doar sangue para qualquer pessoa com qualquer tipo sanguíneo. Quatro por cento dos afro-americanos têm sangue tipo O e um fator RH negativo, 5 a 10% dos afro-americanos têm o fator Rh e 51% têm sangue tipo O.

    Figura\(\PageIndex{10}\):

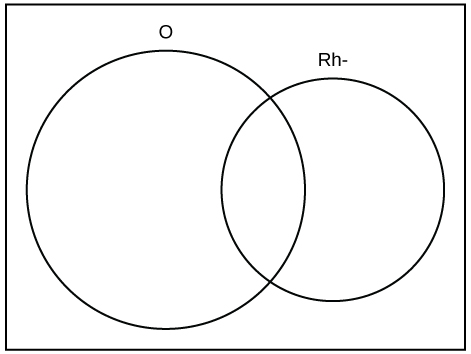
    O círculo “O” representa os afro-americanos com sangue tipo O. O oval “Rh- “representa os afro-americanos com o fator Rh-.

    Vamos pegar a média de 5% e 10% e usar 7,5% como a porcentagem de afro-americanos que têm o fator Rh. Deixe\(\text{O} =\) afro-americano com sangue tipo O e\(\text{R} =\) afro-americano com fator Rh.

    1. \(P(\text{O}) =\)___________
    2. \(P(\text{R}) =\)___________
    3. \(P(\text{O AND R}) =\)___________
    4. \(P(\text{O OR R}) =\)____________
    5. No Diagrama de Venn, descreva a área sobreposta usando uma frase completa.
    6. No Diagrama de Venn, descreva a área no retângulo, mas fora do círculo e do oval usando uma frase completa.

    Responda

    a. 0,51; b. 0,075; c. 0,04; d. 0,545; e. A área representa os afro-americanos que têm sangue do tipo O e o fator Rh. f. A área representa os afro-americanos que não têm sangue tipo O nem fator Rh.

    Exercício\(\PageIndex{7}\)

    Em uma livraria, a probabilidade de o cliente comprar um romance é de 0,6 e a probabilidade de o cliente comprar um livro de não ficção é de 0,4. Suponha que a probabilidade de o cliente comprar os dois seja de 0,2.

    1. Desenhe um diagrama de Venn representando a situação.
    2. Descubra a probabilidade de o cliente comprar um romance ou um livro que não seja de ficção.
    3. No diagrama de Venn, descreva a área sobreposta usando uma frase completa.
    4. Suponha que alguns clientes comprem apenas discos compactos. Desenhe um oval em seu diagrama de Venn representando esse evento.

    Responda

    a. e d. No diagrama de Venn abaixo, o oval azul representa clientes que compram um romance, o oval vermelho representa o cliente que compra não-ficção e o cliente oval amarelo que compra discos compactos.

    Figura\(\PageIndex{11}\):

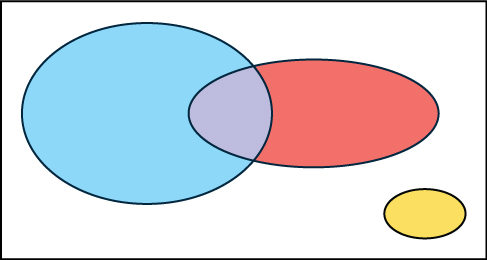
    \(P(\text{novel or non-fiction}) = P(\text{Blue OR Red}) = P(\text{Blue}) + P(\text{Red}) - P(\text{Blue AND Red}) = 0.6 + 0.4 - 0.2 = 0.8\)b.

    c. A área sobreposta do oval azul e do oval vermelho representa os clientes que compram um romance e um livro de não ficção.

    Referências

    1. Dados do Departamento Público do Condado de Clara
    2. Dados da American Cancer Society.
    3. Dados da The Data and Story Library, 1996. Disponível on-line em http://lib.stat.cmu.edu/DASL/ (acessado em 2 de maio de 2013).
    4. Dados da Administração Federal de Rodovias, parte do Departamento de Transporte dos Estados Unidos.
    5. Dados do Departamento de Censo dos Estados Unidos, parte do Departamento de Comércio dos Estados Unidos.
    6. Dados do USA Today.
    7. “Meio ambiente”. Banco Mundial, 2013. Disponível on-line em http://data.worldbank.org/topic/environment (acessado em 2 de maio de 2013).
    8. “Pesquisar conjuntos de dados”. Roper Center: Arquivos de opinião pública, Universidade de Connecticut., 2013. Disponível on-line em www.ropercenter.uconn.edu/data_access/data/search_for_datasets.html (acessado em 2 de maio de 2013).

    Revisão

    Um diagrama de árvore usa ramificações para mostrar os diferentes resultados dos experimentos e facilita a visualização de questões de probabilidade complexas. Um diagrama de Venn é uma imagem que representa os resultados de um experimento. Geralmente consiste em uma caixa que representa o espaço amostral S junto com círculos ou ovais. Os círculos ou ovais representam eventos. Um diagrama de Venn é especialmente útil para visualizar o evento OR, o evento AND e o complemento de um evento e para entender as probabilidades condicionais.

    Glossário

    diagrama de árvore
    a representação visual útil de um espaço amostral e eventos na forma de uma “árvore” com galhos marcados por possíveis resultados, juntamente com probabilidades associadas (frequências, frequências relativas)
    Diagrama de Venn
    a representação visual de um espaço amostral e eventos na forma de círculos ou ovais mostrando suas interseções