2.8: Medidas da disseminação dos dados

Last updated
Save as PDF

Page ID: 190088

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Uma característica importante de qualquer conjunto de dados é a variação nos dados. Em alguns conjuntos de dados, os valores dos dados estão concentrados próximos à média; em outros conjuntos de dados, os valores dos dados são mais amplamente distribuídos da média. A medida mais comum de variação, ou dispersão, é o desvio padrão. O desvio padrão é um número que mede a distância entre os valores dos dados e sua média.

O desvio padrão

fornece uma medida numérica da quantidade geral de variação em um conjunto de dados, e
pode ser usado para determinar se um determinado valor de dados está próximo ou distante da média.

O desvio padrão fornece uma medida da variação geral em um conjunto de dados

O desvio padrão é sempre positivo ou zero. O desvio padrão é pequeno quando os dados estão todos concentrados perto da média, exibindo pouca variação ou dispersão. O desvio padrão é maior quando os valores dos dados estão mais dispersos da média, exibindo mais variação.

Suponha que estejamos estudando a quantidade de tempo que os clientes esperam na fila do caixa no supermercado A e no supermercado B. o tempo médio de espera em ambos os supermercados é de cinco minutos. No supermercado A, o desvio padrão para o tempo de espera é de dois minutos; no supermercado B, o desvio padrão para o tempo de espera é de quatro minutos.

Como o supermercado B tem um desvio padrão maior, sabemos que há mais variação nos tempos de espera no supermercado B. No geral, os tempos de espera no supermercado B estão mais diferentes da média; os tempos de espera no supermercado A estão mais concentrados perto da média.

O desvio padrão pode ser usado para determinar se um valor de dados está próximo ou distante da média.

Suponha que Rosa e Binh façam compras no supermercado A. Rosa espera no balcão do caixa por sete minutos e Binh espera por um minuto. No supermercado A, o tempo médio de espera é de cinco minutos e o desvio padrão é de dois minutos. O desvio padrão pode ser usado para determinar se um valor de dados está próximo ou distante da média.

Rosa espera sete minutos:

Sete é dois minutos a mais do que a média de cinco; dois minutos é igual a um desvio padrão.
O tempo de espera de Rosa de sete minutos é dois minutos a mais do que a média de cinco minutos.
O tempo de espera de Rosa de sete minutos é um desvio padrão acima da média de cinco minutos.

Binh espera por um minuto.

Um é quatro minutos a menos que a média de cinco; quatro minutos é igual a dois desvios padrão.
O tempo de espera de um minuto de Binh é quatro minutos a menos do que a média de cinco minutos.
O tempo de espera de Binh de um minuto é dois desvios padrão abaixo da média de cinco minutos.
Um valor de dados com dois desvios padrão da média está apenas no limite do que muitos estatísticos considerariam estar longe da média. Considerar que os dados estão longe da média se estiverem a mais de dois desvios padrão é mais uma “regra prática” aproximada do que uma regra rígida. Em geral, a forma da distribuição dos dados afeta a quantidade de dados que está mais distante do que dois desvios padrão. (Você aprenderá mais sobre isso nos próximos capítulos.)

A reta numérica pode ajudar você a entender o desvio padrão. Se colocarmos cinco e sete em uma reta numérica, sete está à direita de cinco. Dizemos, então, que sete é um desvio padrão à direita de cinco porque\(5 + (1)(2) = 7\).

Se um também fizesse parte do conjunto de dados, então um são dois desvios padrão à esquerda de cinco porque\(5 + (-2)(2) = 1\).

Isso mostra uma reta numérica em intervalos de 1 de 0 a 7. — Figura\(\PageIndex{1}\)

Em geral, um valor = média + (#ofSTDEV) (desvio padrão)
onde #ofSTDEVs = o número de desvios padrão
#ofSTDEV não precisa ser um número inteiro
Um é dois desvios padrão a menos que a média de cinco porque:\(1 = 5 + (-2)(2)\).

O valor da equação = média + (#ofSTDEVs) (desvio padrão) pode ser expresso para uma amostra e para uma população.

amostra:\[x = \bar{x} + \text{(#ofSTDEV)(s)}\]
População:\[x = \mu + \text{(#ofSTDEV)(s)}\]

A letra minúscula s representa o desvio padrão da amostra e a letra grega\(\sigma\) (sigma, minúscula) representa o desvio padrão da população.

O símbolo\(\bar{x}\) é a média da amostra e o símbolo grego\(\mu\) é a média da população.

Calculando o desvio padrão

Se\(x\) for um número, então a diferença “\(x\)— média” é chamada de desvio. Em um conjunto de dados, há tantos desvios quanto itens no conjunto de dados. Os desvios são usados para calcular o desvio padrão. Se os números pertencerem a uma população, em símbolos, um desvio é\(x - \mu\). Para dados de amostra, em símbolos, um desvio é\(x - \bar{x}\).

O procedimento para calcular o desvio padrão depende se os números são da população inteira ou se são dados de uma amostra. Os cálculos são semelhantes, mas não idênticos. Portanto, o símbolo usado para representar o desvio padrão depende se ele é calculado a partir de uma população ou de uma amostra. A letra minúscula s representa o desvio padrão da amostra e a letra grega\(\sigma\) (sigma, minúscula) representa o desvio padrão da população. Se a amostra tiver as mesmas características da população, então s deve ser uma boa estimativa de\(\sigma\).

Para calcular o desvio padrão, precisamos primeiro calcular a variância. A variância é a média dos quadrados dos desvios (os\(x - \bar{x}\) valores de uma amostra ou os\(x - \mu\) valores de uma população). O símbolo\(\sigma^{2}\) representa a variância da população; o desvio padrão da população\(\sigma\) é a raiz quadrada da variância da população. O símbolo\(s^{2}\) representa a variância da amostra; o desvio padrão da amostra s é a raiz quadrada da variância da amostra. Você pode pensar no desvio padrão como uma média especial dos desvios.

Se os números vierem de um censo de toda a população e não de uma amostra, quando calculamos a média dos desvios quadrados para encontrar a variância, dividimos por\(N\), o número de itens na população. Se os dados forem de uma amostra em vez de uma população, quando calculamos a média dos desvios quadrados, dividimos por n — 1, um a menos que o número de itens na amostra.

Fórmulas para o desvio padrão da amostra

\[s = \sqrt{\dfrac{\sum(x-\bar{x})^{2}}{n-1}} \label{eq1}\]

\[s = \sqrt{\dfrac{\sum f (x-\bar{x})^{2}}{n-1}} \label{eq2}\]

Para o desvio padrão da amostra, o denominador é\(n - 1\), ou seja, o tamanho da amostra MENOS 1.

Fórmulas para o desvio padrão da população

\[\sigma = \sqrt{\dfrac{\sum(x-\mu)^{2}}{N}} \label{eq3} \]

\[\sigma = \sqrt{\dfrac{\sum f (x-\mu)^{2}}{N}} \label{eq4}\]

Para o desvio padrão da população, o denominador é\(N\) o número de itens na população.

Nas Equações\ ref {eq2} e\ ref {eq4},\(f\) representa a frequência com que um valor aparece. Por exemplo, se um valor aparecer uma vez,\(f\) é um. Se um valor aparecer três vezes no conjunto de dados ou na população,\(f\) será três.

Variabilidade amostral de uma estatística

A estatística de uma distribuição amostral foi discutida na Seção 2.6. O quanto a estatística varia de uma amostra para outra é conhecido como a variabilidade amostral de uma estatística. Normalmente, você mede a variabilidade amostral de uma estatística por seu erro padrão.

O erro padrão da média é um exemplo de erro padrão. É um desvio padrão especial e é conhecido como o desvio padrão da distribuição amostral da média. Você abordará o erro padrão da média no Capítulo 7. A notação para o erro padrão da média é\(\dfrac{\sigma}{\sqrt{n}}\) onde\(\sigma\) está o desvio padrão da população e\(n\) é o tamanho da amostra.

Na prática, USE UMA CALCULADORA OU SOFTWARE DE COMPUTADOR PARA CALCULAR O DESVIO PADRÃO. Se você estiver usando uma calculadora TI-83, 83+, 84+, precisará selecionar o desvio padrão apropriado\(\sigma_{x}\) ou a \(s_{x}\)partir das estatísticas resumidas. Vamos nos concentrar em usar e interpretar as informações que o desvio padrão nos fornece. No entanto, você deve estudar o exemplo passo a passo a seguir para ajudá-lo a entender como o desvio padrão mede a variação da média. (As instruções da calculadora aparecem no final deste exemplo.)

Exemplo\(\PageIndex{1}\)

Em uma turma da quinta série, a professora estava interessada na idade média e no desvio padrão da amostra das idades de seus alunos. Os dados a seguir são as idades de uma AMOSTRA de n = 20 alunos da quinta série. As idades são arredondadas para o semestre mais próximo:

9; 9,5; 9,5; 10; 10; 10; 10,5; 10,5; 10,5; 10,5; 11; 11; 11; 11; 11; 11; 11; 11,5; 11,5; 11,5; 11,5;

\[\bar{x} = \dfrac{9+9.5(2)+10(4)+10.5(4)+11(6)+11.5(3)}{20} = 10.525 \nonumber\]

A idade média é de 10,53 anos, arredondada para dois lugares.

A variância pode ser calculada usando uma tabela. Em seguida, o desvio padrão é calculado tomando a raiz quadrada da variância. Explicaremos as partes da tabela depois de calcular s.

Dados	Freq.	Desvios	Desvios ²	*(Freq.) (Desvios* ²)**
x	f	(x —\(\bar{x}\))	(x — 2\(\bar{x}\))	(f) (x — 2\(\bar{x}\))
9	1	9 — 10,525 = —1,525	(—1,525) 2 = 2,325625	1 × 2,325625 = 2,325625
9.5	2	9,5 — 10,525 = —1,025	(^—1,0252) = 1,050625	2 × 1,050625 = 2,101250
10	4	10 — 10,525 = —0,525	(—0,525) ² = 0,275625	4 × 0,275625 = 1,1025
10,5	4	10,5 — 10,525 = —0,025	(^—0,0252) = 0,000625	4 × 0,000625 = 0,0025
11	6	1 — 10,525 = 0,475	(^0,4752) = 0,225625	6 × 0,225625 = 1,35375
11,5	3	11,5 — 10,525 = 0,975	(0,975) ² = 0,950625	3 × 0,950625 = 2,851875
				O total é 9.7375

A variância da amostra\(s^{2}\),, é igual à soma da última coluna (9,7375) dividida pelo número total de valores de dados menos um (20 — 1):

\[s^{2} = \dfrac{9.7375}{20-1} = 0.5125 \nonumber\]

O desvio padrão da amostra s é igual à raiz quadrada da variância da amostra:

\[s = \sqrt{0.5125} = 0.715891 \nonumber\]

e isso é arredondado para duas casas decimais,\(s = 0.72\).

Normalmente, você faz o cálculo do desvio padrão em sua calculadora ou computador. Os resultados intermediários não são arredondados. Isso é feito para garantir a precisão.

Para os problemas a seguir, lembre-se de que o valor = média + (#ofSTDEVs) (desvio padrão). Verifique a média e o desvio padrão ou em uma calculadora ou computador.
Para uma amostra:\(x\) =\(\bar{x}\) + (#ofSTDEVs) (s)
Para uma população:\(x\) =\(\mu\) + (#ofSTDEVs)\(\sigma\)
Neste exemplo, use x =\(\bar{x}\) + (#ofSTDEVs) (s) porque os dados são de uma amostra

Verifique a média e o desvio padrão em sua calculadora ou computador.
Encontre o valor que é um desvio padrão acima da média. Encontre (\(\bar{x}\)+ 1s).
Encontre o valor que está dois desvios padrão abaixo da média. Encontre (\(\bar{x}\)— 2s).
Encontre os valores que são 1,5 desvio padrão (abaixo e acima) da média.

Solução

- Limpe as listas L1 e L2. Pressione STAT 4:CLRList. Insira o 2º 1 para L1, a vírgula (,) e 2º 2 para L2.
- Insira os dados no editor de listas. Pressione STAT 1:EDIT. Se necessário, limpe as listas com a seta para cima até o nome. Pressione CLEAR e seta para baixo.
- Coloque os valores dos dados (9, 9,5, 10, 10,5, 11, 11,5) na lista L1 e as frequências (1, 2, 4, 4, 6, 3) na lista L2. Use as setas do teclado para se movimentar.
- Pressione STAT e seta para CALC. Pressione 1:1 -VarStats e digite L1 (2º 1), L2 (2º 2). Não esqueça a vírgula. Pressione ENTER.
- \(\bar{x}\)= 10,525
- Use Sx porque esses são dados de amostra (não uma população): Sx=0,715891
(\(\bar{x} + 1s) = 10.53 + (1)(0.72) = 11.25\)
\((\bar{x} - 2s) = 10.53 – (2)(0.72) = 9.09\)
- \((\bar{x} - 1.5s) = 10.53 – (1.5)(0.72) = 9.45\)
- \((\bar{x} + 1.5s) = 10.53 + (1.5)(0.72) = 11.61\)

Exercício 2.8.1

Em um time de beisebol, as idades de cada um dos jogadores são as seguintes:

21; 21; 22; 23; 24; 24; 25; 28; 29; 29; 31; 32; 33; 33; 34; 35; 36; 36; 36; 36; 36; 38; 38; 38; 40

Use sua calculadora ou computador para encontrar a média e o desvio padrão. Em seguida, encontre o valor que está dois desvios padrão acima da média.

Resposta

\(\mu\)= 30,68

\(s = 6.09\)

(\(\bar{x} + 2s = 30.68 + (2)(6.09) = 42.86\).

Explicação do cálculo do desvio padrão mostrado na tabela

Os desvios mostram a dispersão dos dados em relação à média. O valor de dados 11,5 está mais distante da média do que o valor de dados 11, que é indicado pelos desvios 0,97 e 0,47. Um desvio positivo ocorre quando o valor dos dados é maior que a média, enquanto um desvio negativo ocorre quando o valor dos dados é menor que a média. O desvio é —1,525 para o valor de dados nove. Se você somar os desvios, a soma é sempre zero. (Por exemplo\(\PageIndex{1}\), há\(n = 20\) desvios.) Portanto, você não pode simplesmente adicionar os desvios para obter a distribuição dos dados. Ao quadrar os desvios, você os torna números positivos, e a soma também será positiva. A variância, então, é o desvio quadrático médio.

A variância é uma medida quadrada e não tem as mesmas unidades dos dados. Tomar a raiz quadrada resolve o problema. O desvio padrão mede a dispersão nas mesmas unidades dos dados.

Observe que, em vez de dividir por\(n = 20\), o cálculo é dividido por\(n - 1 = 20 - 1 = 19\) porque os dados são uma amostra. Para a variância da amostra, dividimos pelo tamanho da amostra menos um (\(n - 1\)). Por que não dividir por\(n\)? A resposta tem a ver com a variação da população. A variância da amostra é uma estimativa da variância da população. Com base na matemática teórica que está por trás desses cálculos, dividir por (\(n - 1\)) fornece uma melhor estimativa da variância da população.

Sua concentração deve estar no que o desvio padrão nos diz sobre os dados. O desvio padrão é um número que mede a distância entre os dados e a média. Deixe uma calculadora ou um computador fazer a aritmética.

O desvio padrão,\(s\) ou\(\sigma\), é zero ou maior que zero. Quando o desvio padrão é zero, não há dispersão; ou seja, todos os valores dos dados são iguais entre si. O desvio padrão é pequeno quando os dados estão todos concentrados perto da média e é maior quando os valores dos dados mostram mais variação da média. Quando o desvio padrão é muito maior que zero, os valores dos dados estão muito dispersos em torno da média; valores atípicos podem\(s\) resultar em valores\(\sigma\) muito grandes.

O desvio padrão, quando apresentado pela primeira vez, pode parecer obscuro. Ao representar graficamente seus dados, você pode ter uma melhor “noção” dos desvios e do desvio padrão. Você descobrirá que em distribuições simétricas, o desvio padrão pode ser muito útil, mas em distribuições distorcidas, o desvio padrão pode não ajudar muito. O motivo é que os dois lados de uma distribuição distorcida têm spreads diferentes. Em uma distribuição distorcida, é melhor observar o primeiro quartil, a mediana, o terceiro quartil, o menor valor e o maior valor. Como os números podem ser confusos, sempre represente graficamente seus dados. Exiba seus dados em um histograma ou gráfico de caixa.

Exemplo\(\PageIndex{2}\)

Use os seguintes dados (notas do primeiro exame) da aula de pré-cálculo de primavera de Susan Dean:

33; 42; 49; 49; 53; 55; 61; 63; 67; 68; 68; 69; 72; 73; 74; 78; 80; 83; 88; 88; 88; 88; 90; 92; 94; 94; 94; 94; 94; 94; 96; 100

Crie um gráfico contendo os dados, as frequências, as frequências relativas e as frequências relativas cumulativas com três casas decimais.
Calcule o seguinte com uma casa decimal usando uma calculadora TI-83+ ou TI-84:
1. A média da amostra
2. O desvio padrão da amostra
3. A mediana
4. O primeiro quartil
5. O terceiro quartil
6. IQR
Construa um gráfico de caixa e um histograma no mesmo conjunto de eixos. Faça comentários sobre o gráfico da caixa, o histograma e o gráfico.

Resposta

Veja a tabela
1. A média da amostra = 73,5
2. O desvio padrão da amostra = 17,9
3. A mediana = 73
4. O primeiro quartil = 61
5. O terceiro quartil = 90
6. IQR = 90 — 61 = 29
O\(x\) eixo -vai de 32,5 a 100,5; o\(y\) eixo -vai de -2,4 a 15 para o histograma. O número de intervalos é cinco, então a largura de um intervalo é (\(100.5 - 32.5\)) dividida por cinco, é igual a 13,6. Os pontos finais dos intervalos são os seguintes: o ponto inicial é 32,5,,\(32.5 + 13.6 = 46.1\),\(46.1 + 13.6 = 59.7\),\(59.7 + 13.6 = 73.3\)\(73.3 + 13.6 = 86.9\),\(86.9 + 13.6 = 100.5 =\) o valor final; Nenhum valor de dados cai em um limite de intervalo.

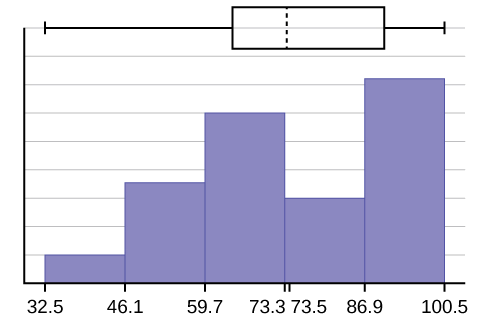
O longo bigode esquerdo no gráfico da caixa é refletido no lado esquerdo do histograma. A distribuição das notas do exame nos 50% mais baixos é maior (\(73 - 33 = 40\)) do que a diferença nos 50% superiores (\(100 - 73 = 27\)). O histograma, o gráfico da caixa e o gráfico refletem isso. Há um número substancial de notas A e B (anos 80, 90 e 100). O histograma mostra isso claramente. O gráfico da caixa mostra que os 50% médios das notas do exame (IQR = 29) são Ds, Cs e Bs. O gráfico da caixa também mostra que os 25% mais baixos das notas do exame são Ds e Fs.

Dados	Frequência	Frequência relativa	Frequência relativa cumulativa
33	1	0,032	0,032
42	1	0,032	0,064
49	2	0,065	0,129
53	1	0,032	0.161
55	2	0,065	0,226
61	1	0,032	0,258
63	1	0,032	0,29
67	1	0,032	0,322
68	2	0,065	0,387
69	2	0,065	0,452
72	1	0,032	0,484
73	1	0,032	0,516
74	1	0,032	0,548
78	1	0,032	0,580
80	1	0,032	0,612
83	1	0,032	0,644
88	3	0,097	0,741
90	1	0,032	0,773
92	1	0,032	0,805
94	4	0,129	0,934
96	1	0,032	0,966
100	1	0,032	0,998 (Por que esse valor não é 1?)

Exercício\(\PageIndex{2}\)

Os dados a seguir mostram os diferentes tipos de lojas de alimentos para animais de estimação na área.

6; 6; 6; 6; 7; 7; 7; 7; 8; 9; 9; 9; 9; 9; 10; 10; 10; 10; 10; 11; 11; 11; 11; 12; 12; 12; 12; 12; 12; 12; 12; 12; 12;

Calcule a média da amostra e o desvio padrão da amostra com uma casa decimal usando uma calculadora TI-83+ ou TI-84.

Resposta

\(\mu = 9.3\)e\(s = 2.2\)

Desvio padrão das tabelas de frequência agrupadas

Lembre-se de que, para dados agrupados, não conhecemos valores de dados individuais, portanto, não podemos descrever o valor típico dos dados com precisão. Em outras palavras, não podemos encontrar a média, a mediana ou o modo exatos. Podemos, no entanto, determinar a melhor estimativa das medidas do centro encontrando a média dos dados agrupados com a fórmula:

\[\text{Mean of Frequency Table} = \dfrac{\sum fm}{\sum f}\]

onde\(f\) frequências de\(m =\) intervalo e pontos médios de intervalo.

Assim como não conseguimos encontrar a média exata, também não podemos encontrar o desvio padrão exato. Lembre-se de que o desvio padrão descreve numericamente o desvio esperado que um valor de dados tem da média. Em inglês simples, o desvio padrão nos permite comparar como os dados individuais “incomuns” são comparados à média.

Exemplo\(\PageIndex{3}\)

Encontre o desvio padrão para os dados na Tabela\(\PageIndex{3}\).

Tabela\(\PageIndex{3}\)
Classe	Frequência, f	Ponto médio, m	m ²	\(\bar{x}\)	fm ²	Desvio padrão
0—2	1	1	1	\ (\ bar {x}\)” style="alinhamento vertical: meio; ">7,58	1	3.5
3—5	6	4	16	\ (\ bar {x}\)” style="alinhamento vertical: meio; ">7,58	96	3.5
6—8	10	7	49	\ (\ bar {x}\)” style="alinhamento vertical: meio; ">7,58	490	3.5
9—11	7	10	100	\ (\ bar {x}\)” style="alinhamento vertical: meio; ">7,58	700	3.5
12—14	0	13	169	\ (\ bar {x}\)” style="alinhamento vertical: meio; ">7,58	0	3.5
15—17	2	16	256	\ (\ bar {x}\)” style="alinhamento vertical: meio; ">7,58	512	3.5

Para esse conjunto de dados, temos a média\(\bar{x}\) = 7,58 e o desvio padrão\(s_{x}\) = 3,5. Isso significa que um valor de dados selecionado aleatoriamente seria de 3,5 unidades da média. Se olharmos para a primeira classe, veremos que o ponto médio da classe é igual a um. Isso é quase dois desvios padrão completos da média, já que 7,58 — 3,5 — 3,5 = 0,58. Embora a fórmula para calcular o desvio padrão não seja complicada,\(s_{x} = \sqrt{\dfrac{f(m - \bar{x})^{2}}{n-1}}\) onde\(s_{x}\) = desvio padrão da amostra,\(\bar{x}\) = média da amostra, os cálculos são entediantes. Geralmente, é melhor usar a tecnologia ao realizar os cálculos.

Encontre o desvio padrão para os dados do exemplo anterior

Classe	0-2	3-5	6-8	9—11	12—14	15—17
Frequência, f	1	6	10	7	0	2

Primeiro, pressione a tecla STAT e selecione 1:Edit

Insira os valores do ponto médio em L1 e as frequências em L2

Selecione STAT, CALC e estatísticas de 1:1-Var

Selecione 2 ^e depois 1, depois 2 ^e depois 2 Enter

Você verá exibidos um desvio padrão da população e o desvio padrão da amostra,\(s_{x}\).\(\sigma_{x}\)

Comparando valores de diferentes conjuntos de dados

O desvio padrão é útil ao comparar valores de dados provenientes de diferentes conjuntos de dados. Se os conjuntos de dados tiverem médias e desvios padrão diferentes, comparar os valores dos dados diretamente pode ser enganoso.

Para cada valor de dados, calcule a quantos desvios padrão de distância de sua média o valor está.
Use a fórmula: valor = média + (#ofSTDEVs) (desvio padrão); resolva para #ofSTDEVs.
\(\text{#ofSTDEVs} = \dfrac{\text{value-mean}}{\text{standard deviation}}\)
Compare os resultados desse cálculo.

#ofSTDEVs geralmente é chamado de "z -score”; podemos usar o símbolo\(z\). Em símbolos, as fórmulas se tornam:

Amostra	\(x = \bar{x} + zs\)	\(z = \dfrac{x - \bar{x}}{s}\)
População	\(x = \mu + z\sigma\)	\(z = \dfrac{x - \mu}{\sigma}\)

Exemplo\(\PageIndex{4}\)

Dois estudantes, John e Ali, de diferentes escolas secundárias, queriam descobrir quem tinha o maior GPA em comparação com sua escola. Qual aluno teve o maior GPA em comparação com sua escola?

Estudante	GPA	GPA médio escolar	Desvio padrão escolar
John	2,85	3,0	0,7
Ali	77	80	10

Resposta

Para cada aluno, determine quantos desvios padrão (#ofSTDEVs) seu GPA está longe da média para sua escola. Preste muita atenção aos sinais ao comparar e interpretar a resposta.

\[z = \text{#ofSTDEVs} = \left(\dfrac{\text{value-mean}}{\text{standard deviation}}\right) = \left(\dfrac{x + \mu}{\sigma}\right) \nonumber\]

Para John,

\[z = \text{#ofSTDEVs} = \left(\dfrac{2.85-3.0}{0.7}\right) = -0.21 \nonumber\]

Para Ali,

\[z = \text{#ofSTDEVs} = (\dfrac{77-80}{10}) = -0.3 \nonumber\]

John tem o melhor GPA em comparação com sua escola porque seu GPA é 0,21 desvios padrão abaixo da média de sua escola, enquanto o GPA de Ali é 0,3 desvios padrão abaixo da média de sua escola.

A pontuação z de John de —0,21 é maior do que a pontuação z de Ali de —0,3. Para o GPA, valores mais altos são melhores, então concluímos que John tem o melhor GPA quando comparado à sua escola.

Exercício\(\PageIndex{4}\)

Duas nadadoras, Angie e Beth, de equipes diferentes, queriam descobrir quem tinha o tempo mais rápido nos 50 metros livres em comparação com sua equipe. Qual nadadora teve o tempo mais rápido em comparação com sua equipe?

Nadador	Tempo (segundos)	Tempo médio da equipe	Desvio padrão da equipe
Angie	26.2	27.2	0,8
Beth	27.3	30.1	1.4

Resposta

Para Angie:

\[z = \left(\dfrac{26.2-27.2}{0.8}\right) = -1.25 \nonumber\]

Para Beth:

\[z = \left(\dfrac{27.3-30.1}{1.4}\right) = -2 \nonumber\]

As listas a seguir fornecem alguns fatos que fornecem um pouco mais de visão sobre o que o desvio padrão nos diz sobre a distribuição dos dados.

Para QUALQUER conjunto de dados, não importa qual seja a distribuição dos dados:

Pelo menos 75% dos dados estão dentro de dois desvios padrão da média.
Pelo menos 89% dos dados estão dentro de três desvios padrão da média.
Pelo menos 95% dos dados estão dentro de 4,5 desvios padrão da média.
Isso é conhecido como Regra de Chebyshev.

Para dados com uma distribuição em forma de sino e simétrica:

Aproximadamente 68% dos dados estão dentro de um desvio padrão da média.
Aproximadamente 95% dos dados estão dentro de dois desvios padrão da média.
Mais de 99% dos dados estão dentro de três desvios padrão da média.
Isso é conhecido como Regra Empírica.
É importante observar que essa regra só se aplica quando a forma da distribuição dos dados é em forma de sino e simétrica. Aprenderemos mais sobre isso ao estudar a distribuição de probabilidade “Normal” ou “Gaussiana” em capítulos posteriores.

Referências

Dados do Microsoft Bookshelf.
Rei, Bill. “Falando graficamente”. Pesquisa institucional, Faculdade Comunitária de Lake Tahoe. Disponível on-line em www.ltcc.edu/web/about/institutional-research (acessado em 3 de abril de 2013).

Revisão

O desvio padrão pode ajudar você a calcular a dispersão dos dados. Existem diferentes equações a serem usadas se você estiver calculando o desvio padrão de uma amostra ou de uma população.

O desvio padrão nos permite comparar dados ou classes individuais com a média do conjunto de dados numericamente.
\(s = \sqrt{\dfrac{\sum(x-\bar{x})^{2}}{n-1}}\)ou\(s = \sqrt{\dfrac{\sum f (x-\bar{x})^{2}}{n-1}}\) é a fórmula para calcular o desvio padrão de uma amostra. Para calcular o desvio padrão de uma população, usaríamos a média da população,\(\mu\), e a fórmula\(\sigma = \sqrt{\dfrac{\sum(x-\mu)^{2}}{N}}\) ou\(\sigma = \sqrt{\dfrac{\sum f (x-\mu)^{2}}{N}}\). 4 f (x − μ) 2 N − − − − − − − − − √.

Revisão da fórmula

\[s_{x} = \sqrt{\dfrac{\sum fm^{2}}{n} - \bar{x}^2}\]

onde\(s_{x} \text{sample standard deviation}\) e\(\bar{x} = \text{sample mean}\)

Use as informações a seguir para responder aos próximos dois exercícios: Os dados a seguir são as distâncias entre 20 lojas de varejo e um grande centro de distribuição. As distâncias estão em milhas.

29; 37; 38; 40; 58; 67; 68; 69; 76; 86; 87; 95; 96; 96; 99; 106; 112; 127; 145; 150

Exercício 2.8.4

Use uma calculadora gráfica ou um computador para encontrar o desvio padrão e arredondar para o décimo mais próximo.

Resposta

\(s\)= 34,5

Exercício 2.8.5

Encontre o valor que é um desvio padrão abaixo da média.

Exercício 2.8.6

Dois jogadores de beisebol, Fredo e Karl, de equipes diferentes queriam descobrir quem tinha a maior média de rebatidas em comparação com seu time. Qual jogador de beisebol teve a maior média de rebatidas em comparação com seu time?

Jogador de baseball	Média de rebatidas	Média de rebatidas da equipe	Desvio padrão da equipe
Fredo	0,158	0.166	0,012
Karl	0,177	0,189	0,015

Resposta

Para Fredo:

\(z\)=\(\dfrac{0.158-0.166}{0.012}\) = —0,67

Para Karl:

\(z\)=\(\dfrac{0.177-0.189}{0.015}\) = —0,8

A pontuação z de Fredo de —0,67 é maior do que a pontuação z de Karl de —0,8. Para a média de rebatidas, valores mais altos são melhores, então Fredo tem uma média de rebatidas melhor em comparação com sua equipe.

Exercício 2.8.7

Use a Tabela para encontrar o valor que é de três desvios padrão:

acima da média
abaixo da média

Encontre o desvio padrão para as seguintes tabelas de frequência usando a fórmula. Verifique os cálculos com a TI 83/84.

Exercício 2.8.5

Encontre o desvio padrão para as seguintes tabelas de frequência usando a fórmula. Verifique os cálculos com a TI 83/84.

Grau	Frequência
49,5 a 59,5	2
59,5 a 69,5	3
69,5 a 79,5	8
79,5 a 89,5	12
89,5 a 99,5	5

Baixa temperatura diária	Frequência
49,5 a 59,5	53
59,5 a 69,5	32
69,5 a 79,5	15
79,5 a 89,5	1
89,5 a 99,5	0

Pontos por jogo	Frequência
49,5 a 59,5	14
59,5 a 69,5	32
69,5 a 79,5	15
79,5 a 89,5	23
89,5 a 99,5	2

Resposta

\(s_{x} = \sqrt{\dfrac{\sum fm^{2}}{n} - \bar{x}^{2}} = \sqrt{\dfrac{193157.45}{30} - 79.5^{2}} = 10.88\)
\(s_{x} = \sqrt{\dfrac{\sum fm^{2}}{n} - \bar{x}^{2}} = \sqrt{\dfrac{380945.3}{101} - 60.94^{2}} = 7.62\)
\(s_{x} = \sqrt{\dfrac{\sum fm^{2}}{n} - \bar{x}^{2}} = \sqrt{\dfrac{440051.5}{86} - 70.66^{2}} = 11.14\)

Reunindo tudo

Exercício 2.8.7

Vinte e cinco estudantes selecionados aleatoriamente foram questionados sobre o número de filmes que assistiram na semana anterior. Os resultados são os seguintes:

Nº de filmes	Frequência
0	5
1	9
2	6
3	4
4	1

Encontre a média da amostra\(\bar{x}\).
Encontre o desvio padrão aproximado da amostra,\(s\).

Resposta

1,48
1,12

Exercício 2.8.8

Quarenta estudantes selecionados aleatoriamente foram questionados sobre o número de pares de tênis que eles possuíam. Deixe\(X =\) o número de pares de tênis que você possui. Os resultados são os seguintes:

\(X\)	Frequência y
\ (X\) ">1	2
\ (X\) ">2	5
\ (X\) ">3	8
\ (X\) ">4	12
\ (X\) ">5	12
\ (X\) ">6	0
\ (X\) ">7	1

Encontre a média da amostra\(\bar{x}\)
Encontre os desvios padrão da amostra, s
Construa um histograma dos dados.
Preencha as colunas do gráfico.
Encontre o primeiro quartil.
Encontre a mediana.
Encontre o terceiro quartil.
Construa um gráfico de caixa dos dados.
Qual porcentagem dos estudantes possuía pelo menos cinco pares?
Encontre o ^40º percentil.
Encontre o ^90º percentil.
Construa um gráfico de linhas dos dados
Construa um diagrama dos dados

Exercício 2.8.9

A seguir estão os pesos publicados (em libras) de todos os membros da equipe do San Francisco 49ers de um ano anterior.

177; 205; 210; 210; 232; 205; 185; 185; 178; 210; 206; 212; 184; 174; 185; 242; 188; 212; 215; 247; 241; 223; 220; 260; 245; 259; 278; 270; 280; 295; 275; 285; 285; 290; 272; 273; 280; 285; 285; 290; 272; 273; 280; 285; 285; 290; 272; 273; 280; 285; 285; 290; 272; 273; 280; 285 5; 286; 200; 215; 185; 230; 250; 241; 190; 260; 250; 302; 265; 290; 276; 228; 265

Organize os dados do menor para o maior valor.
Encontre a mediana.
Encontre o primeiro quartil.
Encontre o terceiro quartil.
Construa um gráfico de caixa dos dados.
Os 50% médios dos pesos são de _______ a _______.
Se nossa população fosse toda jogadora profissional de futebol, os dados acima seriam uma amostra de pesos ou a população de pesos? Por quê?
Se nossa população incluísse todos os membros da equipe que já jogaram pelo San Francisco 49ers, os dados acima seriam uma amostra de pesos ou a população de pesos? Por quê?
Suponha que a população fosse do San Francisco 49ers. Encontre:
1. a população significa,\(\mu\).
2. o desvio padrão da população,\(\sigma\).
3. o peso que está dois desvios padrão abaixo da média.
4. Quando Steve Young, zagueiro, jogou futebol, ele pesava 205 libras. Quantos desvios padrão acima ou abaixo da média ele estava?
Nesse mesmo ano, o peso médio do Dallas Cowboys foi de 240,08 libras com um desvio padrão de 44,38 libras. Emmit Smith pesava 209 libras. Com relação à sua equipe, quem era mais leve, Smith ou Young? Como você determinou sua resposta?

Resposta

174; 177; 178; 184; 185; 185; 185; 185; 188; 190; 200; 205; 205; 206; 210; 210; 210; 212; 212; 215; 215; 220; 223; 228; 230; 232; 241; 241; 242; 245; 247; 250; 250; 259; 260; 260; 265; 241; 242; 245; 247; 250; 250; 259; 260; 260; 265; 265; 265; 265; 265; 265; 265; 265; 265; 265; 5; 270; 272; 273; 275; 276; 278; 280; 280; 285; 285; 286; 290; 290; 295; 302
241
205,5
272,5
205,5, 272,5
amostra
população
1. 236,34
2. 37,50
3. 161,34
4. 0,84 std. dev. abaixo da média
Jovem

Exercício 2.8.10

Cem professores participaram de um seminário sobre resolução de problemas matemáticos. As atitudes de uma amostra representativa de 12 professores foram medidas antes e depois do seminário. Um número positivo para mudança de atitude indica que a atitude do professor em relação à matemática se tornou mais positiva. As 12 pontuações de alteração são as seguintes:

3; 8; —1; 2; 0; 5; —3; 1; —1; 6; 5; —2

Qual é a pontuação média de alteração?
Qual é o desvio padrão para essa população?
Qual é a pontuação média de mudança?
Encontre a pontuação de alteração que é 2,2 desvios padrão abaixo da média.

Exercício 2.8.11

Consulte a Figura para determinar quais das seguintes opções são verdadeiras e quais são falsas. Explique sua solução para cada parte em frases completas.

Isso mostra três gráficos. O primeiro é um histograma com um modo de 3 e distribuição bastante simétrica entre 1 (valor mínimo) e 5 (valor máximo). O segundo gráfico é um histograma com picos em 1 (valor mínimo) e 5 (valor máximo) com 3 tendo a menor frequência. O terceiro gráfico é um gráfico de caixa. O primeiro bigode se estende de 0 a 1. A caixa começa no primeiro quartil, 1, e termina no terceiro quartil,6. Uma linha vertical tracejada marca a mediana em 3. O segundo bigode se estende das 6 em diante. — Figura\(\PageIndex{6}\).

</figure>

As medianas dos três gráficos são as mesmas.
Não podemos determinar se alguma das médias dos três gráficos é diferente.
O desvio padrão para o gráfico b é maior do que o desvio padrão para o gráfico a.
Não podemos determinar se algum dos terceiros quartis dos três gráficos é diferente.

Resposta

É verdade
É verdade
É verdade
Falso

Exercício 2.8.12

Em uma edição recente do IEEE Spectrum, 84 conferências de engenharia foram anunciadas. Quatro conferências duraram dois dias. Trinta e seis duraram três dias. Dezoito duraram quatro dias. Dezenove duraram cinco dias. Quatro duraram seis dias. Um durou sete dias. Um durou oito dias. Um durou nove dias. Seja X = a duração (em dias) de uma conferência de engenharia.

Organize os dados em um gráfico.
Encontre a mediana, o primeiro quartil e o terceiro quartil.
Encontre o ^65º percentil.
Encontre o ^10º percentil.
Construa um gráfico de caixa dos dados.
A metade média das conferências duram de _______ dias a _______ dias.
Calcule a média da amostra de dias de conferências de engenharia.
Calcule o desvio padrão da amostra de dias de conferências de engenharia.
Encontre o modo.
Se você estivesse planejando uma conferência de engenharia, qual você escolheria como duração da conferência: média; mediana; ou modo? Explique por que você fez essa escolha.
Dê duas razões pelas quais você acha que três a cinco dias parecem ser períodos populares de conferências de engenharia.

Exercício 2.8.13

Uma pesquisa sobre matrículas em 35 faculdades comunitárias nos Estados Unidos produziu os seguintes números:

6414; 1550; 2109; 9350; 21828; 4300; 5944; 5722; 2825; 2044; 5481; 5200; 5853; 2750; 10012; 6357; 27000; 9414; 7681; 3200; 17500; 9200; 7380; 18314; 6557; 13713; 1768; 7493; 2771; 2861; 1263; 7285; 28165; 5080; 11622

Organize os dados em um gráfico com cinco intervalos de igual largura. Identifique as duas colunas como “Inscrição” e “Frequência”.
Construa um histograma dos dados.
Se você construísse uma nova faculdade comunitária, qual informação seria mais valiosa: a modalidade ou a média?
Calcule a média da amostra.
Calcule o desvio padrão da amostra.
Uma escola com uma matrícula de 8000 estaria a quantos desvios padrão da média?

Resposta

Inscrição	Frequência
1000-5000	10
5000-10000	16
10000-15000	3
15000-20000	3
2000-25000	1
25000-30000	2

Verifique a solução do aluno.
modo
8628,74
6943,88
—0,09

Use as informações a seguir para responder aos próximos dois exercícios. \(X =\)o número de dias por semana em que 100 clientes usam uma instalação de exercícios específica.

\(x\)	Frequência
\ (x\) ">0	3
\ (x\) ">1	12
\ (x\) ">2	33
\ (x\) ">3	28
\ (x\) ">4	11
\ (x\) ">5	9
\ (x\) ">6	4

Exercício 2.8.14

O ^80º percentil é _____

Exercício 2.8.15

O número que é 1,5 desvio padrão ABAIXO da média é aproximadamente _____

0,7
4.8
—2,8
Não pode ser determinado

Resposta

uma

Exercício 2.8.16

Suponha que um editor tenha conduzido uma pesquisa perguntando aos consumidores adultos o número de livros de ficção em brochura que eles compraram no mês anterior. Os resultados estão resumidos na tabela.

Nº de livros	Freq.	Rel. Freq.
0	18
1	24
2	24
3	22
4	15
5	10
7	5
9	1

Há alguma diferença nos dados? Use um teste numérico apropriado envolvendo o IQR para identificar valores atípicos, se houver, e indicar claramente sua conclusão.
Se um valor de dados for identificado como um valor atípico, o que deve ser feito a respeito?
Algum valor de dados está a mais de dois desvios padrão da média? Em algumas situações, os estatísticos podem usar esses critérios para identificar valores de dados que são incomuns, em comparação com outros valores de dados. (Observe que esse critério é mais apropriado para dados em forma de montículo e simétricos, em vez de dados assimétricos.)
As partes a e c desse problema dão a mesma resposta?
Examine a forma dos dados. Qual parte, a ou c, dessa pergunta fornece um resultado mais apropriado para esses dados?
Com base na forma dos dados, qual é a medida de centro mais apropriada para esses dados: média, mediana ou modo?

Glossário

Desvio padrão: um número que é igual à raiz quadrada da variância e mede a que distância os valores dos dados estão de sua média; notação: s para desvio padrão da amostra e σ para desvio padrão da população.

Contribuidores e atribuições

Variância: média dos desvios quadrados da média, ou o quadrado do desvio padrão; para um conjunto de dados, um desvio pode ser representado como \(x\)—\(\bar{x}\) onde\(x\) é um valor dos dados e\(\bar{x}\) é a média da amostra. A variância da amostra é igual à soma dos quadrados dos desvios dividida pela diferença do tamanho amostral e um.

Template:ContribOpenStax