5.2: A distribuição uniforme
- Page ID
- 186789
A distribuição uniforme é uma distribuição contínua de probabilidade e está relacionada a eventos que têm a mesma probabilidade de ocorrer. Ao resolver problemas que tenham uma distribuição uniforme, tenha cuidado ao observar se os dados são inclusivos ou exclusivos dos endpoints.
A declaração matemática da distribuição uniforme é
\(f(x) = \frac{1}{b-a}\)para\(a \leq x \leq b\)
onde\(a =\) o menor valor de\(x\) e\(b =\) o maior valor de\(x\).
As fórmulas para a média teórica e o desvio padrão são
\(\mu=\frac{a+b}{2}\)e\(\sigma=\sqrt{\frac{(b-a)^{2}}{12}}\)
Exercício\(\PageIndex{1}\)
Os dados a seguir são o número de passageiros em 35 barcos de pesca fretados diferentes. A média da amostra = 7,9 e o desvio padrão da amostra = 4,33. Os dados seguem uma distribuição uniforme em que todos os valores entre zero e 14, incluindo, são igualmente prováveis. Declare os valores de\(a\)\(b\) e. Escreva a distribuição na notação correta e calcule a média teórica e o desvio padrão.
\ (\ PageIndex {1}\) “>| 1 | 12 | 4 | 10 | 4 | 14 | 11 |
| 7 | 11 | 4 | 13 | 2 | 4 | 6 |
| 3 | 10 | 0 | 12 | 6 | 9 | 10 |
| 5 | 13 | 4 | 10 | 14 | 12 | 11 |
| 6 | 10 | 11 | 0 | 11 | 13 | 2 |
-
Tabela 5.1
Exemplo\(\PageIndex{2}\)
A quantidade de tempo, em minutos, que uma pessoa deve esperar por um ônibus é distribuída uniformemente entre zero e 15 minutos, inclusive.
a. Qual é a probabilidade de uma pessoa esperar menos de 12,5 minutos?
- Responda
-
a. Seja\(X\) = o número de minutos que uma pessoa deve esperar por um ônibus. \(a = 0\)\(b = 15\)e. \(X \sim U(0, 15)\). Escreva a função de densidade de probabilidade. \(f(x) = \frac{1}{15-0}=\frac{1}{15}\)para\(0 \leq x \leq 15\).
Encontre\(P(x < 12.5)\). Desenhe um gráfico.
\[P(x<k)=\text { (base) (height) }=(12.5-0)\left(\frac{1}{15}\right)=0.8333\nonumber\]
A probabilidade de uma pessoa esperar menos de 12,5 minutos é de 0,8333.
Figura 5.11
b. Em média, quanto tempo uma pessoa deve esperar? Encontre a média\(\mu\), e o desvio padrão,\(\sigma\).
- Responda
-
\(\mu=\frac{a+b}{2}=\frac{15+0}{2}=7.5\)b. Em média, uma pessoa deve esperar 7,5 minutos.
\(\sigma=\sqrt{\frac{(b-a)^{2}}{12}}=\sqrt{\frac{(15-\theta)^{2}}{12}}=4.3\). O desvio padrão é de 4,3 minutos.
c. Noventa por cento das vezes, o tempo que uma pessoa deve esperar cai abaixo de qual valor?
Nota
Isso pede o percentil 90.
- Responda
-
c. Encontre o 90º percentil. Desenhe um gráfico. Deixe\(k =\) o 90º percentil.
\ (P (x )<k) >
\(0.90=(k)\left(\frac{1}{15}\right)\)
\(k=(0.90)(15)=13.5\)
O 90º percentil é 13,5 minutos. Noventa por cento das vezes, uma pessoa deve esperar no máximo 13,5 minutos.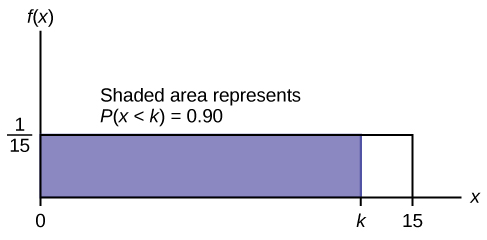 Figura\(\PageIndex{12}\)
Figura\(\PageIndex{12}\)
Exercício\(\PageIndex{2}\)
A duração total dos jogos de beisebol na liga principal na temporada de 2011 é distribuída uniformemente entre 447 horas e 521 horas, inclusive.
- Encontre\(a\)\(b\) e descreva o que eles representam.
- Escreva a distribuição.
- Encontre a média e o desvio padrão.
- Qual é a probabilidade de que a duração dos jogos de uma equipe na temporada de 2011 seja entre 480 e 500 horas?


