5.2: Resolver sistemas de equações por substituição
- Page ID
- 184022
Ao final desta seção, você poderá:
- Resolva um sistema de equações por substituição
- Resolva aplicações de sistemas de equações por substituição
Antes de começar, faça este teste de prontidão.
- Simplifique −5 (3−x).
Se você perdeu esse problema, revise o Exercício 1.10.43. - Simplifique 4−2 (n+5).
Se você perdeu esse problema, revise o Exercício 1.10.41. - Resolva y. 8y−8=32−2y
Se você perdeu esse problema, revise o Exercício 2.3.22. - Resolva x. 3x−9y=−3
Se você perdeu esse problema, revise o Exercício 2.6.22.
Resolver sistemas de equações lineares por meio de gráficos é uma boa maneira de visualizar os tipos de soluções que podem resultar. No entanto, há muitos casos em que resolver um sistema por meio de gráficos é inconveniente ou impreciso. Se os gráficos se estenderem além da pequena grade com x e y entre −10 e 10, representar graficamente as linhas pode ser complicado. E se as soluções para o sistema não forem números inteiros, pode ser difícil ler seus valores com precisão em um gráfico.
Nesta seção, resolveremos sistemas de equações lineares pelo método de substituição.
Resolva um sistema de equações por substituição
Usaremos o mesmo sistema que usamos primeiro para representar graficamente.
\(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)
Primeiro resolveremos uma das equações para x ou y. Podemos escolher qualquer uma das equações e resolver qualquer uma das variáveis, mas tentaremos fazer uma escolha que facilite o trabalho.
Em seguida, substituímos essa expressão na outra equação. O resultado é uma equação com apenas uma variável — e sabemos como resolvê-las!
Depois de encontrarmos o valor de uma variável, substituiremos esse valor em uma das equações originais e resolveremos a outra variável. Finalmente, verificamos nossa solução e garantimos que ela torne as duas equações verdadeiras.
Vamos preencher todas essas etapas agora no Exercício\(\PageIndex{1}\).
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)
- Resposta
-






Resolva o sistema por substituição. \(\left\{\begin{array}{l}{-2 x+y=-11} \\ {x+3 y=9}\end{array}\right.\)
- Resposta
-
(6,1)
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{x+3 y=10} \\ {4 x+y=18}\end{array}\right.\)
- Resposta
-
(4,2)
- Resolva uma das equações para qualquer variável.
- Substitua a expressão da Etapa 1 pela outra equação.
- Resolva a equação resultante.
- Substitua a solução na Etapa 3 em uma das equações originais para encontrar a outra variável.
- Escreva a solução como um par ordenado.
- Verifique se o par ordenado é uma solução para ambas as equações originais.
Se uma das equações no sistema for dada na forma de inclinação e interceptação, a Etapa 1 já está concluída! Veremos isso no Exercício\(\PageIndex{4}\).
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{x+y=-1} \\ {y=x+5}\end{array}\right.\)
- Resposta
-
A segunda equação já está resolvida para y. Substituiremos a expressão no lugar de y na primeira equação.
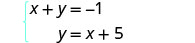
A segunda equação já está resolvida para y.
Vamos substituir na primeira equação.Substitua o y por x + 5. 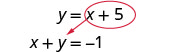
Resolva a equação resultante para x. 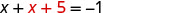
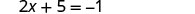
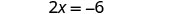
Substitua x = −3 em y = x + 5 para encontrar y. 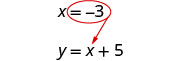
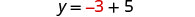
O par ordenado é (−3, 2). 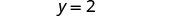
Verifique o par ordenado nas duas equações:
\(\begin{array} {rllrll} x+y &=&-1 & y&=&x+5\\-3+2 &\stackrel{?}{=}&-1 &2& \stackrel{?}{=} & -3 + 5\\-1 &=&-1\checkmark &2 &=&2\checkmark \end{array}\)A solução é (−3, 2).
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{x+y=6} \\ {y=3 x-2}\end{array}\right.\)
- Resposta
-
(2,4)
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{2 x-y=1} \\ {y=-3 x-6}\end{array}\right.\)
- Resposta
-
(−1, −3)
Se as equações forem dadas na forma padrão, precisaremos começar resolvendo uma das variáveis. Neste próximo exemplo, resolveremos a primeira equação para y.
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{3 x+y=5} \\ {2 x+4 y=-10}\end{array}\right.\)
- Resposta
-
Precisamos resolver uma equação para uma variável. Em seguida, substituiremos essa expressão na outra equação.
Resolva para y.
Substitua na outra equação.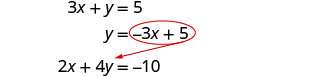
Substitua o y por −3 x + 5. 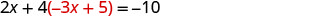
Resolva a equação resultante para x. 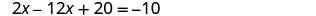
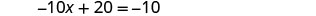
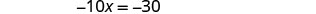
Substitua x = 3 em 3 x + y = 5 para encontrar y. 


O par ordenado é (3, −4). 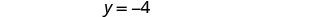
Verifique o par ordenado nas duas equações:
\(\begin{array} {rllrll} 3x+y &=&5 & 2x+4y&=&-10\\3\cdot3+(-4) &\stackrel{?}{=}&5 &2\cdot3 + 4(-4)& \stackrel{?}{=} & -10\\9-4&\stackrel{?}{=}&5 &6-16& \stackrel{?}{=} & -10\\5 &=&5\checkmark &-10&=&-10\checkmark \end{array}\)A solução é (3, −4).
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{4 x+y=2} \\ {3 x+2 y=-1}\end{array}\right.\)
- Resposta
-
(1, −2)
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{-x+y=4} \\ {4 x-y=2}\end{array}\right.\)
- Resposta
-
(2,6)
No Exercício,\(\PageIndex{7}\) foi mais fácil resolver y na primeira equação porque ela tinha um coeficiente de 1. No Exercício\(\PageIndex{10}\), será mais fácil resolver x.
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{x-2 y=-2} \\ {3 x+2 y=34}\end{array}\right.\)
- Resposta
-
Resolveremos a primeira equação para xx e depois substituiremos a expressão na segunda equação.

Resolva para x.
Substitua na outra equação.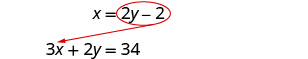
Substitua o x por 2 y − 2. 
Resolva a equação resultante para y. 
Substitua y = 5 em x − 2 y = −2 para encontrar x.

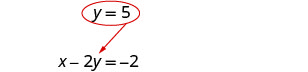



O par pedido é (8, 5). Verifique o par ordenado nas duas equações:
\(\begin{array} {rllrll} x-2y &=&-2 & 3x+2y&=&34\\8-2\cdot 5 &\stackrel{?}{=}&-2 &3\cdot8 + 2\cdot5& \stackrel{?}{=} & 34\\8-10&\stackrel{?}{=}&-2 &24+10& \stackrel{?}{=} & 34\\-2 &=&-2\checkmark &34&=&34\checkmark \end{array}\)A solução é (8, 5).
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{x-5 y=13} \\ {4 x-3 y=1}\end{array}\right.\)
- Resposta
-
(−2, −3)
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{x-6 y=-6} \\ {2 x-4 y=4}\end{array}\right.\)
- Resposta
-
(6,2)
Quando as duas equações já estão resolvidas para a mesma variável, é fácil substituí-la!
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{y=-2 x+5} \\ {y=\frac{1}{2} x}\end{array}\right.\)
- Resposta
-
Como ambas as equações são resolvidas para y, podemos substituir uma pela outra.
\(\frac{1}{2}x\)Substitua y na primeira equação. 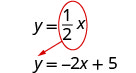
Substitua o y por\(\frac{1}{2}x\) 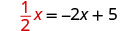
Resolva a equação resultante. Comece
limpando a fração.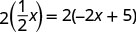
Resolva para x. 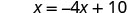
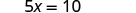
Substitua x = 2 em\(y = \frac{1}{2}x\) para encontrar y. 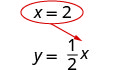
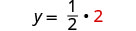
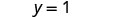
O par encomendado é (2,1). Verifique o par ordenado nas duas equações:
\(\begin{array} {rllrll} y &=&\frac{1}{2}x & y&=&-2x+5\\1 &\stackrel{?}{=}&\frac{1}{2}\cdot2 &1& \stackrel{?}{=} & -2\cdot2+5\\1 &=&1\checkmark &1 &=&-4+5\\ &&&1&=&1\checkmark \end{array}\)A solução é (2,1).
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{y=3 x-16} \\ {y=\frac{1}{3} x}\end{array}\right.\)
- Resposta
-
(6,2)
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{y=-x+10} \\ {y=\frac{1}{4} x}\end{array}\right.\)
- Resposta
-
(8,2)
Tenha muito cuidado com os sinais no próximo exemplo.
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{4 x+2 y=4} \\ {6 x-y=8}\end{array}\right.\)
- Resposta
-
Precisamos resolver uma equação para uma variável. Resolveremos a primeira equação para y.

Resolva a primeira equação para y. 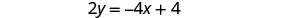
Substitua −2 x + 2 por y na segunda equação. 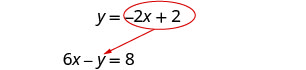
Substitua o y por −2 x + 2. 
Resolva a equação para x. 


Substitua\(x = \frac{5}{4}\) em 4 x + 2 y = 4 para encontrar y.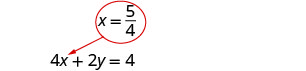



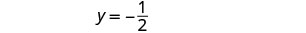
O par pedido é\((\frac{5}{4},−\frac{1}{2})\). Verifique o par ordenado nas duas equações.
\(\begin{array} {rllrll} 4x+2y &=&4& 6x-y&=&8\\4(\frac{5}{4}) +2(-\frac{1}{2})&\stackrel{?}{=}&4 &6(\frac{5}{4}) - (-\frac{1}{2})& \stackrel{?}{=} & 8\\5-1&\stackrel{?}{=}&4 &\frac{15}{4} - (-\frac{1}{2}) &\stackrel{?}{=} & 8\\4 &=&4\checkmark &\frac{16}{2} &\stackrel{?}{=}&8\\ &&&8&=&8\checkmark \end{array}\)A solução é (54, −12).
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{x-4 y=-4} \\ {-3 x+4 y=0}\end{array}\right.\)
- Resposta
-
\((2,\frac{3}{2})\)
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{4 x-y=0} \\ {2 x-3 y=5}\end{array}\right.\)
- Resposta
-
\((−\frac{1}{2},−2)\)
No exemplo, será necessário um pouco mais de trabalho para resolver uma equação para x ou y.
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{4 x-3 y=6} \\ {15 y-20 x=-30}\end{array}\right.\)
- Resposta
-
Precisamos resolver uma equação para uma variável. Resolveremos a primeira equação para x.
Como 0 = 0 é uma afirmação verdadeira, o sistema é consistente. As equações são dependentes. Os gráficos dessas duas equações forneceriam a mesma linha. O sistema tem infinitas soluções.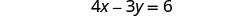
Resolva a primeira equação para x. 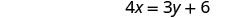
\(\frac{3}{4} y+\frac{3}{2}\)Substitua x na segunda equação. 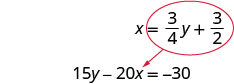
Substitua o x por\(\frac{3}{4} y+\frac{3}{2}\) 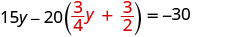
Resolva para y. 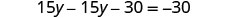
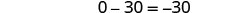

Resolva o sistema por substituição. \(\left\{\begin{array}{l}{2 x-3 y=12} \\ {-12 y+8 x=48}\end{array}\right.\)
- Resposta
-
infinitas soluções
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{5 x+2 y=12} \\ {-4 y-10 x=-24}\end{array}\right.\)
- Resposta
-
infinitas soluções
Examine as equações no Exercício\(\PageIndex{22}\). Existe alguma maneira de reconhecer que eles estão na mesma linha?
Vamos ver o que acontece no próximo exemplo.
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{5 x-2 y=-10} \\ {y=\frac{5}{2} x}\end{array}\right.\)
- Resposta
-
A segunda equação já está resolvida para y, então podemos substituir y na primeira equação.
Como 0 = −10 é uma afirmação falsa, as equações são inconsistentes. Os gráficos das duas equações seriam linhas paralelas. O sistema não tem soluções.Substitua x por y na primeira equação. 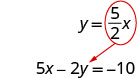
Substitua o y por\(\frac{5}{2}x\). 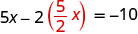
Resolva para x. 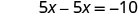

Resolva o sistema por substituição. \(\left\{\begin{array}{l}{3 x+2 y=9} \\ {y=-\frac{3}{2} x+1}\end{array}\right.\)
- Resposta
-
sem solução
Resolva o sistema por substituição. \(\left\{\begin{array}{l}{5 x-3 y=2} \\ {y=\frac{5}{3} x-4}\end{array}\right.\)
- Resposta
-
sem solução
Resolva aplicações de sistemas de equações por substituição
Vamos copiar aqui a estratégia de resolução de problemas que usamos na seção Resolvendo Sistemas de Equações por Gráficos para resolver sistemas de equações. Agora que sabemos como resolver sistemas por substituição, é isso que faremos na Etapa 5.
- Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas.
- Identifique o que estamos procurando.
- Diga o que estamos procurando. Escolha variáveis para representar essas quantidades.
- Traduza em um sistema de equações.
- Resolva o sistema de equações usando boas técnicas de álgebra.
- Verifique a resposta do problema e verifique se faz sentido.
- Responda à pergunta com uma frase completa.
Algumas pessoas acham mais fácil configurar problemas de palavras com duas variáveis do que configurá-los com apenas uma variável. Escolher os nomes das variáveis é mais fácil quando tudo o que você precisa fazer é anotar duas letras. Pense nisso no próximo exemplo: como você teria feito isso com apenas uma variável?
A soma de dois números é zero. Um número é nove a menos que o outro. Encontre os números.
- Resposta
-
Etapa 1. Leia o problema. Etapa 2. Identifique o que estamos procurando. Estamos procurando dois números. Etapa 3. Diga o que estamos procurando. Seja n= o primeiro número
Deixe m= o segundo númeroEtapa 4. Traduza em um sistema de equações. A soma de dois números é zero. 
Um número é nove a menos que o outro. 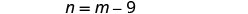
O sistema é: 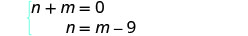
Etapa 5. Resolva o sistema de
equações. Usaremos a substituição,
pois a segunda equação é resolvida
para n.Substitua m − 9 por n na primeira equação. 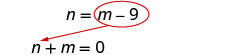
Resolva para mim. 


Substitua\(m=\frac{9}{2}\) na segunda equação
e resolva por n.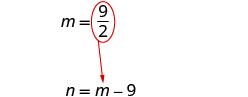
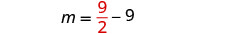
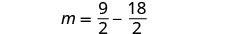
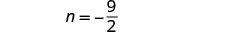
Etapa 6. Verifique a resposta no problema. Esses números fazem sentido
no problema? Vamos deixar isso para você!Etapa 7. Responda à pergunta. Os números são\(\frac{9}{2}\)\(-\frac{9}{2}\) e.
A soma de dois números é 10. Um número é 4 a menos que o outro. Encontre os números.
- Resposta
-
Os números são 3 e 7.
A soma de dois números é −6. Um número é 10 a menos que o outro. Encontre os números.
- Resposta
-
Os números são 2 e −8.
No Exercício\(\PageIndex{28}\), usaremos a fórmula para o perímetro de um retângulo, P = 2 L + 2 W.
Adicione o texto dos exercícios aqui.
- Resposta
-
Etapa 1. Leia o problema. 
Etapa 2. Identifique o que você está procurando. Estamos procurando o comprimento e a largura. Etapa 3. Diga o que estamos procurando. Seja L= o comprimento
W= a larguraEtapa 4. Traduza em um sistema de equações. O perímetro de um retângulo é 88. 2 L + 2 W = P
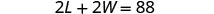
O comprimento é cinco a mais do que o dobro da largura. 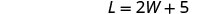
O sistema é: 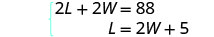
Etapa 5. Resolva o sistema de equações.
Usaremos a substituição, pois a segunda
equação foi resolvida para L.
Substitua 2 W + 5 por L na primeira equação.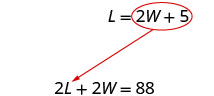
Resolva para W. 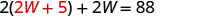
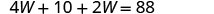
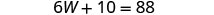
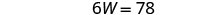
Substitua W = 13 na segunda
equação e resolva por L.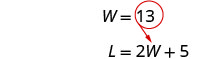
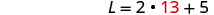
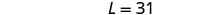
Etapa 6. Verifique a resposta no problema. Um retângulo com comprimento 31 e largura
13 tem perímetro 88? Sim.Etapa 7. Responda à equação. O comprimento é 31 e a largura é 13.
O perímetro de um retângulo é 40. O comprimento é 4 a mais que a largura. Encontre o comprimento e a largura do retângulo.
- Resposta
-
O comprimento é 12 e a largura é 8.
O perímetro de um retângulo é 58. O comprimento é 5 a mais do que três vezes a largura. Encontre o comprimento e a largura do retângulo.
- Resposta
-
O comprimento é 23 e a largura é 6.
Para o Exercício,\(\PageIndex{31}\) precisamos lembrar que a soma das medidas dos ângulos de um triângulo é de 180 graus e que um triângulo reto tem um ângulo de 90 graus.
A medida de um dos pequenos ângulos de um triângulo reto é dez a mais do que três vezes a medida do outro ângulo pequeno. Encontre as medidas dos dois ângulos.
- Resposta
-
Vamos desenhar e rotular uma figura.
Etapa 1. Leia o problema. 
Etapa 2. Identifique o que você está procurando. Estamos procurando as medidas dos ângulos. Etapa 3. Diga o que estamos procurando. Seja a= a medida do 1º ângulo
b= a medida do 2º ânguloEtapa 4. Traduza em um sistema de equações. A medida de um dos pequenos ângulos
de um triângulo reto é dez a mais do que três
vezes a medida do outro ângulo pequeno.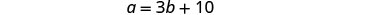
A soma das medidas dos ângulos de
um triângulo é 180.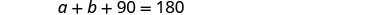
O sistema é: 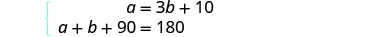
Etapa 5. Resolva o sistema de equações.
Usaremos a substituição, pois a primeira
equação foi resolvida para a.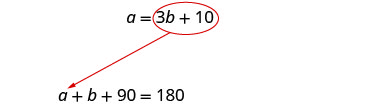
Substitua 3 b + 10 por a na
segunda equação.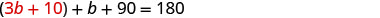
Resolva para b. 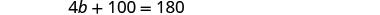


Substitua b = 20 na primeira
equação e resolva por a.

Etapa 6. Verifique a resposta no problema. Vamos deixar isso para você! Etapa 7. Responda à pergunta. As medidas dos ângulos pequenos são
20 e 70.
A medida de um dos pequenos ângulos de um triângulo reto é 2 a mais que 3 vezes a medida do outro ângulo pequeno. Encontre a medida dos dois ângulos.
- Responda
-
A medida dos ângulos é de 22 graus e 68 graus.
A medida de um dos pequenos ângulos de um triângulo reto é 18 menor que o dobro da medida do outro ângulo pequeno. Encontre a medida dos dois ângulos.
- Responda
-
A medida dos ângulos é de 36 graus e 54 graus.
Heather recebeu duas opções de salário como treinadora na academia. A opção A pagaria a ela $25.000 mais $15 por cada sessão de treinamento. A opção B pagaria a ela $10.000 + $40 por cada sessão de treinamento. Quantas sessões de treinamento tornariam as opções salariais iguais?
- Responda
-
Etapa 1. Leia o problema. Etapa 2. Identifique o que você está procurando. Estamos procurando o número de sessões de treinamento
que tornariam o salário igual.Etapa 3. Diga o que estamos procurando. Vamos = salário de Heather.
n= o número de sessões de treinamentoEtapa 4. Traduza em um sistema de equações. A opção A pagaria a ela $25.000 mais $15
por cada sessão de treinamento.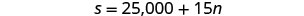
A opção B pagaria a ela $10.000 + $40
por cada sessão de treinamento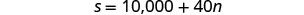
O sistema é: 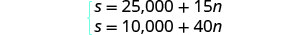
Etapa 5. Resolva o sistema de equações.
Usaremos a substituição.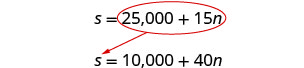
Substitua 25.000 + 15 n por s na segunda equação. 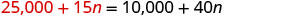
Resolva para n. 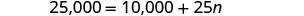
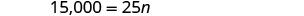

Etapa 6. Verifique a resposta. 600 sessões de treinamento por ano são razoáveis?
As duas opções são iguais quando n = 600?Etapa 7. Responda à pergunta. As opções salariais seriam iguais para 600 sessões de treinamento.
Geraldine recebeu ofertas de vagas de duas seguradoras. A primeira empresa paga um salário de $12.000 mais uma comissão de $100 por cada apólice vendida. O segundo paga um salário de $20.000 mais uma comissão de $50 por cada apólice vendida. Quantas apólices precisariam ser vendidas para que o pagamento total fosse o mesmo?
- Responda
-
Seriam necessárias 160 apólices vendidas para que o pagamento total fosse o mesmo.
Atualmente, Kenneth vende ternos para a empresa A com um salário de $22.000 mais uma comissão de $10 por cada terno vendido. A empresa B oferece a ele uma posição com um salário de $28.000 mais uma comissão de $4 por cada terno vendido. Quantos ternos Kenneth precisaria vender para que as opções fossem iguais?
- Responda
-
Kenneth precisaria vender 1.000 ternos.
Acesse esses recursos on-line para obter instruções e práticas adicionais na resolução de sistemas de equações por substituição.
Conceitos-chave
- Resolva um sistema de equações por substituição
- Resolva uma das equações para qualquer variável.
- Substitua a expressão da Etapa 1 pela outra equação.
- Resolva a equação resultante.
- Substitua a solução na Etapa 3 em uma das equações originais para encontrar a outra variável.
- Escreva a solução como um par ordenado.
- Verifique se o par ordenado é uma solução para ambas as equações originais.


