5.1: Resolva sistemas de equações por meio de gráficos
- Page ID
- 184069
Ao final desta seção, você poderá:
- Determine se um par ordenado é uma solução de um sistema de equações
- Resolva um sistema de equações lineares representando graficamente
- Determine o número de soluções do sistema linear
- Resolva aplicações de sistemas de equações por meio de gráficos
Antes de começar, faça este teste de prontidão.
- Pois a equação\(y=\frac{2}{3}x−4\)
ⓐ é (6,0) uma solução? ⓑ é (−3, −2) uma solução?
Se você perdeu esse problema, revise o Exercício 2.1.1. - Encontre a inclinação e o intercepto y da linha 3x−y=12.
Se você perdeu esse problema, revise o Exercício 4.5.7. - Encontre os interceptos x e y da linha 2x−3y=12.
Se você perdeu esse problema, revise o Exercício 4.3.7.
Determine se um par ordenado é uma solução de um sistema de equações
Na seção Resolvendo equações e desigualdades lineares, aprendemos como resolver equações lineares com uma variável. Lembre-se de que a solução de uma equação é um valor da variável que faz uma afirmação verdadeira quando substituída pela equação. Agora vamos trabalhar com sistemas de equações lineares, duas ou mais equações lineares agrupadas.
Quando duas ou mais equações lineares são agrupadas, elas formam um sistema de equações lineares.
Vamos focar nosso trabalho aqui em sistemas de duas equações lineares em duas incógnitas. Posteriormente, você poderá resolver sistemas maiores de equações.
Um exemplo de um sistema de duas equações lineares é mostrado abaixo. Usamos uma chave para mostrar que as duas equações estão agrupadas para formar um sistema de equações.
\[\begin{cases}{2 x+y=7} \\ {x-2 y=6}\end{cases}\]
Uma equação linear em duas variáveis, como 2 x + y = 7, tem um número infinito de soluções. Seu gráfico é uma linha. Lembre-se de que cada ponto na linha é uma solução para a equação e cada solução para a equação é um ponto na linha.
Para resolver um sistema de duas equações lineares, queremos encontrar os valores das variáveis que são soluções para ambas as equações. Em outras palavras, estamos procurando os pares ordenados (x, y) que tornam as duas equações verdadeiras. Essas são chamadas de soluções para um sistema de equações.
As soluções de um sistema de equações são os valores das variáveis que tornam todas as equações verdadeiras. Uma solução de um sistema de duas equações lineares é representada por um par ordenado (x, y).
Para determinar se um par ordenado é uma solução para um sistema de duas equações, substituímos os valores das variáveis em cada equação. Se o par ordenado tornar as duas equações verdadeiras, é uma solução para o sistema.
Vamos considerar o sistema abaixo:
\[\begin{cases}{3x−y=7} \\ {x−2y=4}\end{cases}\]
O par ordenado (2, −1) é uma solução?
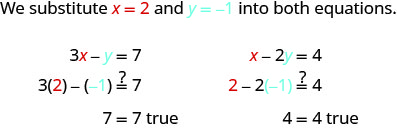
O par ordenado (2, −1) tornou ambas as equações verdadeiras. Portanto, (2, −1) é uma solução para esse sistema.
Vamos tentar outro par encomendado. O par pedido (3, 2) é uma solução?
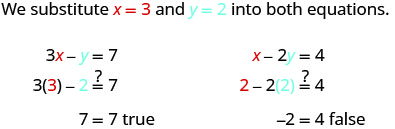
O par ordenado (3, 2) tornou uma equação verdadeira, mas tornou a outra equação falsa. Como não é uma solução para ambas as equações, não é uma solução para esse sistema.
Determine se o par pedido é uma solução para o sistema:\(\begin{cases}{x−y=−1} \\ {2x−y=−5}\end{cases}\)
- (−2, −1)
- (−4, −3)
- Resposta
-
1.
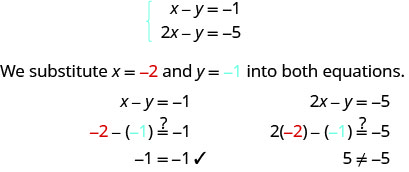
(−2, −1) não torna ambas as equações verdadeiras. (−2, −1) não é uma solução.
2.
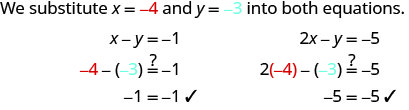
(−4, −3) não torna ambas as equações verdadeiras. (−4, −3) é uma solução.
Determine se o par pedido é uma solução para o sistema:\(\begin{cases}{3x+y=0} \\ {x+2y=−5}\end{cases}\)
- (1, −3)
- (0,0)
- Resposta
-
- sim
- não
Determine se o par pedido é uma solução para o sistema:\(\begin{cases}{x−3y=−8} \\ {−3x−y=4}\end{cases}\)
- (2, −2)
- (−2,2)
- Resposta
-
- não
- sim
Resolva um sistema de equações lineares por meio de gráficos
Neste capítulo, usaremos três métodos para resolver um sistema de equações lineares. O primeiro método que usaremos é a representação gráfica. O gráfico de uma equação linear é uma linha. Cada ponto na linha é uma solução para a equação. Para um sistema de duas equações, representaremos graficamente duas linhas. Então, podemos ver todos os pontos que são soluções para cada equação. E, ao descobrir o que as linhas têm em comum, encontraremos a solução para o sistema.
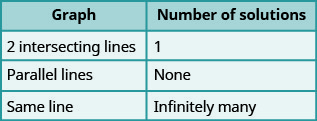
A maioria das equações lineares em uma variável tem uma solução, mas vimos que algumas equações, chamadas contradições, não têm soluções e para outras equações, chamadas identidades, todos os números são soluções. Da mesma forma, quando resolvemos um sistema de duas equações lineares representadas por um gráfico de duas linhas no mesmo plano, há três casos possíveis, conforme mostrado na Figura\(\PageIndex{1}\):
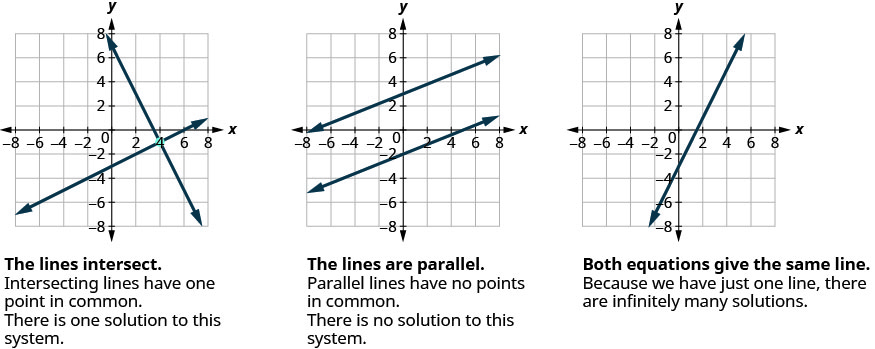
Para o primeiro exemplo de resolução de um sistema de equações lineares nesta seção e nas próximas duas seções, resolveremos o mesmo sistema de duas equações lineares. Mas usaremos um método diferente em cada seção. Depois de ver o terceiro método, você decidirá qual método era a maneira mais conveniente de resolver esse sistema.
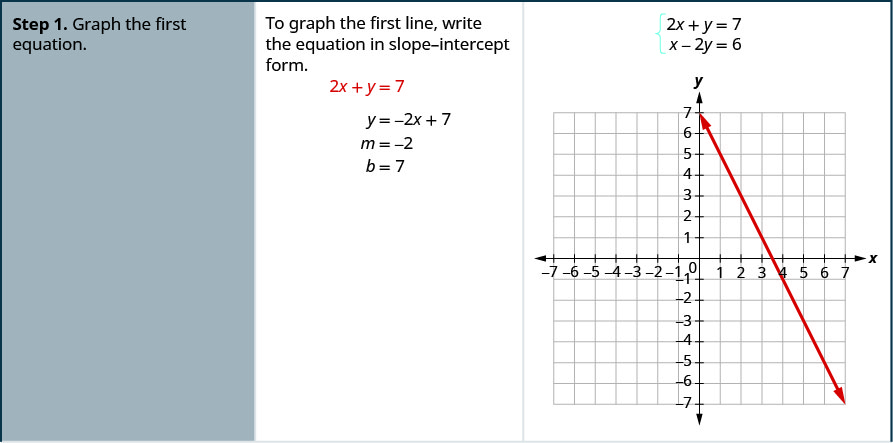
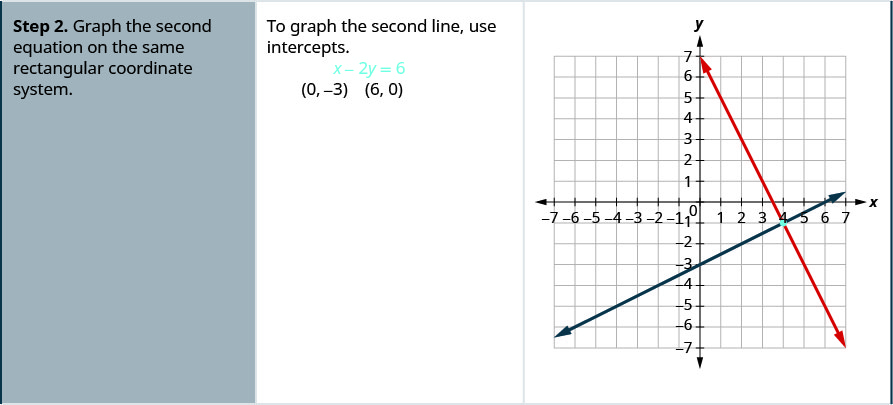
Resolva o sistema representando graficamente:\(\begin{cases}{2x+y=7} \\ {x−2y=6}\end{cases}\)
- Resposta
-


Resolva cada sistema representando graficamente:\(\begin{cases}{x−3y=−3} \\ {x+y=5}\end{cases}\)
- Resposta
-
(3,2)
Resolva cada sistema representando graficamente:\(\begin{cases}{−x+y=1} \\ {3x+2y=12}\end{cases}\)
- Resposta
-
(2,3)
As etapas a serem usadas para resolver um sistema de equações lineares por meio de gráficos são mostradas abaixo.
- Faça um gráfico da primeira equação.
- Faça um gráfico da segunda equação no mesmo sistema de coordenadas retangulares.
- Determine se as linhas se cruzam, são paralelas ou são a mesma linha.
- Identifique a solução para o sistema.
- Se as linhas se cruzarem, identifique o ponto de interseção. Verifique se é uma solução para ambas as equações. Essa é a solução para o sistema.
- Se as linhas estiverem paralelas, o sistema não tem solução.
- Se as linhas forem iguais, o sistema tem um número infinito de soluções.
Resolva o sistema representando graficamente:\(\begin{cases}{y=2x+1} \\ {y=4x−1}\end{cases}\)
- Resposta
-
Ambas as equações neste sistema estão na forma de interceptação de inclinação, então usaremos suas inclinações e interceptações y para representá-las graficamente. \(\begin{cases}{y=2x+1} \\ {y=4x−1}\end{cases}\)
Encontre a inclinação e a interceptação y da
primeira equação.
Encontre a inclinação e a interceptação y da
primeira equação.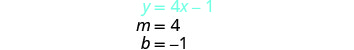
Faça um gráfico das duas linhas. Determine o ponto de interseção. As linhas se cruzam em (1, 3). 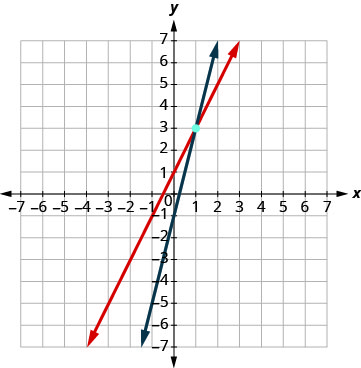
Verifique a solução nas duas equações. \(\begin{array}{l}{y=2 x+1} & {y = 4x - 1}\\{3\stackrel{?}{=}2 \cdot 1+1} &{3\stackrel{?}{=}4 \cdot 1-1} \\ {3=3 \checkmark}&{3=3 \checkmark} \end{array}\) A solução é (1, 3).
Resolva o sistema representando graficamente:\(\begin{cases}{y=2x+2} \\ {y=-x−4}\end{cases}\)
- Resposta
-
(−2, −2)
Resolva o sistema representando graficamente:\(\begin{cases}{y=3x+3} \\ {y=-x+7}\end{cases}\)
- Resposta
-
(1,6)
Ambas as equações no Exercício\(\PageIndex{7}\) foram dadas na forma de inclinação-intercepto. Isso facilitou a criação de gráficos rápidos das linhas. No próximo exemplo, primeiro reescreveremos as equações na forma inclinação-interceptação.
Resolva o sistema representando graficamente:\(\begin{cases}{3x+y=−1} \\ {2x+y=0}\end{cases}\)
- Resposta
-
Resolveremos essas duas equações para yy para que possamos facilmente representá-las graficamente usando suas inclinações e interceptações y. \(\begin{cases}{3x+y=−1} \\ {2x+y=0}\end{cases}\)
Resolva a primeira equação para y.
Encontre a inclinação e a interceptação y.
Resolva a segunda equação para y.
Encontre a inclinação e a interceptação y.\(\begin{aligned} 3 x+y &=-1 \\ y &=-3 x-1 \\ m &=-3 \\ b &=-1 \\ 2 x+y &=0 \\ y &=-2 x \\ b &=0 \end{aligned}\) Faça um gráfico das linhas. 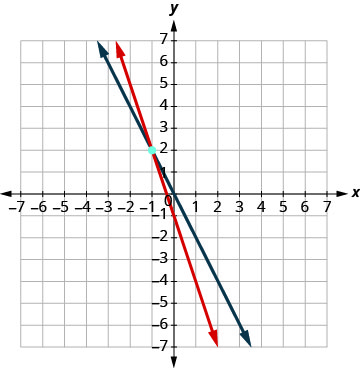
Determine o ponto de interseção. As linhas se cruzam em (−1, 2). Verifique a solução nas duas equações. \(\begin{array}{rllrll}{3x+y}&{=}&{-1} & {2x +y}&{=}&{0}\\{3(-1)+ 2}&{\stackrel{?}{=}}&{-1} &{2(-1)+2}&{\stackrel{?}{=}}&{0} \\ {-1}&{=}&{-1 \checkmark}&{0}&{=}&{0 \checkmark} \end{array}\) A solução é (−1, 2).
Resolva cada sistema representando graficamente:\(\begin{cases}{−x+y=1} \\ {2x+y=10}\end{cases}\)
- Resposta
-
(3,4)
Resolva cada sistema representando graficamente:\(\begin{cases}{ 2x+y=6} \\ {x+y=1}\end{cases}\)
- Resposta
-
(5, −4)
Normalmente, quando as equações são dadas na forma padrão, a maneira mais conveniente de representá-las graficamente é usando os interceptos. Faremos isso no Exercício\(\PageIndex{13}\).
Resolva o sistema representando graficamente:\(\begin{cases}{x+y=2} \\ {x−y=4}\end{cases}\)
- Resposta
-
Encontraremos os interceptos x e y de ambas as equações e os usaremos para representar graficamente as linhas.
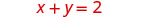
Para encontrar as interceptações, deixe x = 0 e resolva
para y, depois deixe y = 0 e resolva para x.\(\begin{aligned} x+y &=2 \quad x+y=2 \\ 0+y &=2 \quad x+0=2 \\ y &=2 \quad x=2 \end{aligned}\) 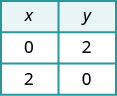
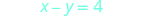
Para encontrar as interceptações, deixe
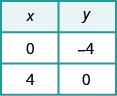
x = 0 e depois y = 0.\ begin {array} {rlr} {x-y} & {=4} & {x-y} & {= 4}\\ {0-y} & {=4} & {x-0} & {=4}\\ {-y} & {=4} & {x} & {=4}\\ {y} & {=-4}\ end {array}
Faça um gráfico da linha. 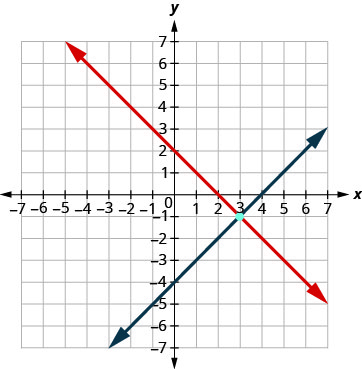
Determine o ponto de interseção. As linhas se cruzam em (3, −1). Verifique a solução nas duas equações. \(\begin{array}{rllrll}{x+y}&{=}&{2} & {x-y}&{=}&{4}\\{3+(-1)}&{\stackrel{?}{=}}&{2} &{3 - (-1)}&{\stackrel{?}{=}}&{4} \\ {2}&{=}&{2 \checkmark}&{4}&{=}&{4 \checkmark} \end{array}\)
A solução é (3, −1).
Resolva cada sistema representando graficamente:\(\begin{cases}{x+y=6} \\ {x−y=2}\end{cases}\)
- Resposta
-
(4,2)
Resolva cada sistema representando graficamente:\(\begin{cases}{x+y=2} \\ {x−y=-8}\end{cases}\)
- Resposta
-
(5, −3)
Você se lembra de como representar graficamente uma equação linear com apenas uma variável? Será uma linha vertical ou horizontal.
Resolva o sistema representando graficamente:\(\begin{cases}{y=6} \\ {2x+3y=12}\end{cases}\)
- Resposta
-

Sabemos que a primeira equação representa uma
linha horizontal cujo intercepto y é 6.
A segunda equação é mais convenientemente representada graficamente
usando interceptações.
Para encontrar os interceptos, deixe x = 0 e então y = 0. 
Faça um gráfico das linhas. 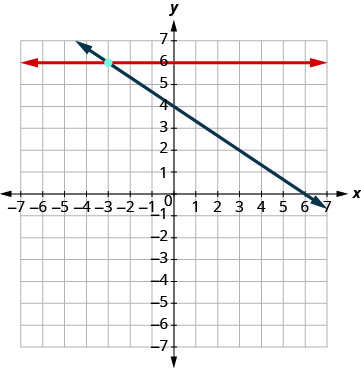
Determine o ponto de interseção. As linhas se cruzam em (−3, 6). Verifique a solução para ambas as equações. \(\begin{array}{rllrll}{y}&{=}&{6} & {2x+3y}&{=}&{12}\\{6}&{\stackrel{?}{=}}&{6} &{2(-3) + 3(6)}&{\stackrel{?}{=}}&{12} \\ {6}&{=}&{6 \checkmark} &{-6+18}&{\stackrel{?}{=}}&{12} \\ {}&{}&{}&{12}&{=}&{12 \checkmark} \end{array}\) A solução é (−3, 6).
Resolva cada sistema representando graficamente:\(\begin{cases}{y=−1} \\ {x+3y=6}\end{cases}\)
- Resposta
-
(9, −1)
Resolva cada sistema representando graficamente:\(\begin{cases}{x=4} \\ {3x−2y=24}\end{cases}\)
- Resposta
-
(4,−6)
Em todos os sistemas de equações lineares até agora, as linhas se cruzaram e a solução foi um ponto. Nos próximos dois exemplos, veremos um sistema de equações que não tem solução e um sistema de equações que tem um número infinito de soluções.
Resolva o sistema representando graficamente:\(\begin{cases}{y=\frac{1}{2}x−3} \\ {x−2y=4}\end{cases}\)
- Resposta
-
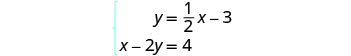
Para representar graficamente a primeira equação,
usaremos sua inclinação e intercepto y.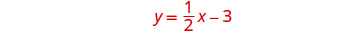
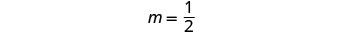
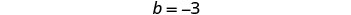
Para representar graficamente a segunda equação,
usaremos os interceptos.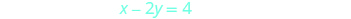
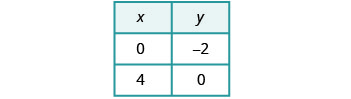
Faça um gráfico das linhas. 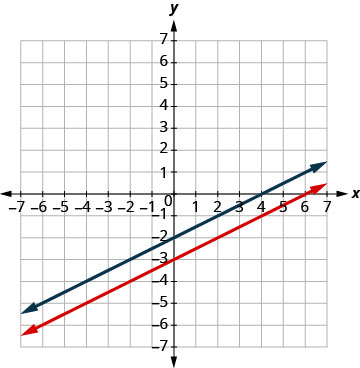
Determine o ponto de interseção. As linhas são paralelas. Como nenhum ponto está nas duas linhas, não há um par ordenado
que torne ambas as equações verdadeiras. Não há solução para
esse sistema.
Resolva cada sistema representando graficamente:\(\begin{cases}{y=-\frac{1}{4}x+2} \\ {x+4y=-8}\end{cases}\)
- Resposta
-
sem solução
Resolva cada sistema representando graficamente:\(\begin{cases}{y=3x−1} \\ {6x−2y=6}\end{cases}\)
- Resposta
-
sem solução
Resolva o sistema representando graficamente:\(\begin{cases}{y=2x−3} \\ {−6x+3y=−9}\end{cases}\)
- Resposta
-
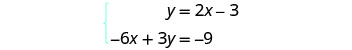
Encontre a inclinação e a interceptação y da
primeira equação.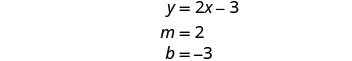
Encontre os interceptos da segunda equação. 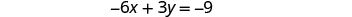
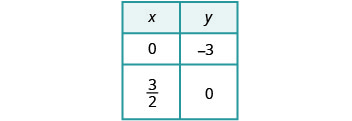
Faça um gráfico das linhas. 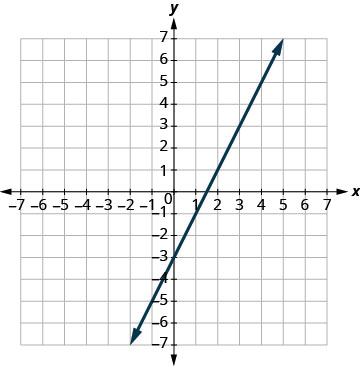
Determine o ponto de interseção. As linhas são as mesmas! Como cada ponto na reta torna as duas equações
verdadeiras, há infinitos pares ordenados que tornam
ambas as equações verdadeiras.Existem infinitas soluções para esse sistema.
Resolva cada sistema representando graficamente:\(\begin{cases}{y=−3x−6} \\ {6x+2y=−12}\end{cases}\)
- Resposta
-
infinitas soluções
Resolva cada sistema representando graficamente:\(\begin{cases}{y=\frac{1}{2}x−4} \\ {2x−4y=16}\end{cases}\)
- Resposta
-
infinitas soluções
Se você escrever a segunda equação\(\PageIndex{22}\) em Exercício na forma de interceptação de inclinação, poderá reconhecer que as equações têm a mesma inclinação e o mesmo intercepto y.
Quando representamos graficamente a segunda linha no último exemplo, nós a desenhamos logo acima da primeira linha. Dizemos que as duas linhas são coincidentes. As linhas coincidentes têm a mesma inclinação e o mesmo intercepto y.
As linhas coincidentes têm a mesma inclinação e o mesmo intercepto y.
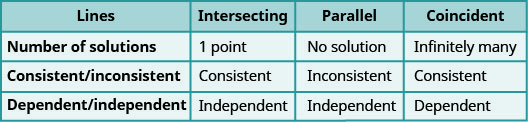
Determine o número de soluções de um sistema linear
Haverá momentos em que quereremos saber quantas soluções existirão para um sistema de equações lineares, mas talvez não precisemos realmente encontrar a solução. Será útil determinar isso sem representar graficamente.
Vimos que duas linhas no mesmo plano devem se cruzar ou são paralelas. \(\PageIndex{16}\)Todos os sistemas de equações em Exercício\(\PageIndex{4}\) a Exercício tinham duas linhas que se cruzam. Cada sistema tinha uma solução.
Um sistema com linhas paralelas, como o Exercise\(\PageIndex{19}\), não tem solução. O que aconteceu no Exercício\(\PageIndex{22}\)? As equações têm linhas coincidentes e, portanto, o sistema tinha infinitas soluções.
Organizaremos esses resultados na Figura\(\PageIndex{2}\) abaixo:
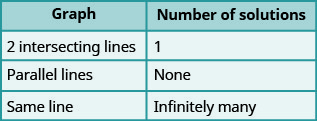
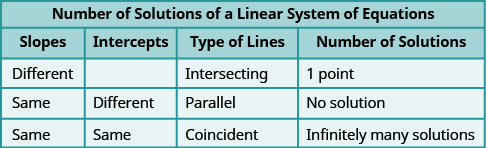
As linhas paralelas têm a mesma inclinação, mas diferentes interceptações y. Então, se escrevermos as duas equações em um sistema de equações lineares em forma de inclinação e interceptação, podemos ver quantas soluções haverá sem a representação gráfica! Veja o sistema que resolvemos no Exercício\(\PageIndex{19}\).
\(\begin{array} {cc} & \begin{cases}{y=\frac{1}{2}x−3} \\ {x−2y=4}\end{cases}\\ \text{The first line is in slope–intercept form.} &\text { If we solve the second equation for } y, \text { we get } \\ &x-2 y =4 \\ y = \frac{1}{2}x -3& x-2 y =-x+4 \\ &y =\frac{1}{2} x-2 \\ m=\frac{1}{2}, b=-3&m=\frac{1}{2}, b=-2 \end{array}\)
As duas retas têm a mesma inclinação, mas interceptações y diferentes. São linhas paralelas.
\(\PageIndex{3}\)A figura mostra como determinar o número de soluções de um sistema linear observando as inclinações e interceptações.
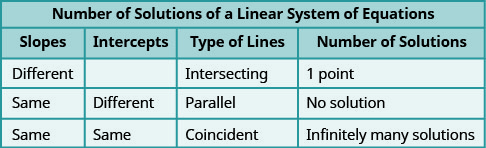
Vamos dar mais uma olhada em nossas equações no Exercício\(\PageIndex{19}\) que nos deram linhas paralelas.
\ [\ begin {casos} {y=\ frac {1} {2} x−3}\\ {x−2y=4}\ end {casos}\)]
Quando ambas as linhas estavam na forma de interceptação de inclinação, tínhamos:
\[y=\frac{1}{2} x-3 \quad y=\frac{1}{2} x-2\]
Você reconhece que é impossível ter um único par ordenado (x, y) que seja uma solução para ambas as equações?
Chamamos um sistema de equações como esse de sistema inconsistente. Não tem solução.
Um sistema de equações que tem pelo menos uma solução é chamado de sistema consistente.
Um sistema consistente de equações é um sistema de equações com pelo menos uma solução.
Um sistema de equações inconsistente é um sistema de equações sem solução.
Também categorizamos as equações em um sistema de equações chamando-as de independentes ou dependentes. Se duas equações são equações independentes, cada uma delas tem seu próprio conjunto de soluções. As linhas que se cruzam e as linhas paralelas são independentes.
Se duas equações são dependentes, todas as soluções de uma equação também são soluções da outra equação. Quando representamos graficamente duas equações dependentes, obtemos linhas coincidentes.
Duas equações são independentes se tiverem soluções diferentes.
Duas equações são dependentes se todas as soluções de uma equação também forem soluções da outra equação.
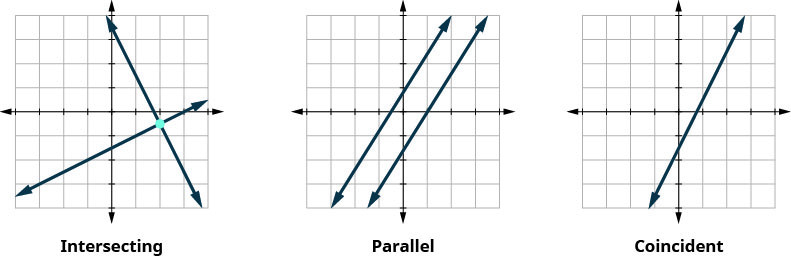
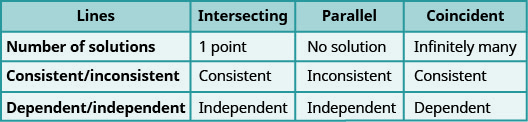
Vamos resumir isso examinando os gráficos dos três tipos de sistemas. Veja a Figura\(\PageIndex{4}\) e a Figura\(\PageIndex{5}\).
Sem representar graficamente, determine o número de soluções e depois classifique o sistema de equações:\(\begin{cases}{y=3x−1} \\ {6x−2y=12}\end{cases}\)
- Resposta
-
\(\begin{array}{lrrl} \text{We will compare the slopes and intercepts} & \begin{cases}{y=3x−1} \\ {6x−2y=12}\end{cases} \\ \text{of the two lines.} \\ \text{The first equation is already in} \\ \text{slope-intercept form.} \\ & {y = 3x - 1}\\ \text{Write the second equation in} \\ \text{slope–intercept form.} \\ & 6x-2y &=&12 \\ & -2y &=& -6x - 12 \\ &\frac{-2y}{-2} &=& \frac{-6x + 12}{-2}\\ &y&=&3x-6\\\\ \text{Find the slope and intercept of each line.} & y = 3x-1 & y=3x-6 \\ &m = 3 & m = 3 \\&b=-1 &b=-6 \\ \text{Since the slopes are the same andy-intercepts} \\ \text{are different, the lines are parallel.}\end{array}\)
Um sistema de equações cujos gráficos são linhas paralelas não tem solução e é inconsistente e independente.
Sem representar graficamente, determine o número de soluções e depois classifique o sistema de equações.
\(\begin{cases}{y=−2x−4} \\ {4x+2y=9}\end{cases}\)
- Resposta
-
sem solução, inconsistente, independente
Sem representar graficamente, determine o número de soluções e depois classifique o sistema de equações.
\(\begin{cases}{y=\frac{1}{3}x−5} \\ {x-3y=6}\end{cases}\)
- Resposta
-
sem solução, inconsistente, independente
Sem representar graficamente, determine o número de soluções e depois classifique o sistema de equações:\(\begin{cases}{2x+y=−3} \\ {x−5y=5}\end{cases}\)
- Resposta
-
\(\begin{array}{lrrlrl} \text{We will compare the slopes and intercepts} & \begin{cases}{2x+y=-3} \\ {x−5y=5}\end{cases} \\ \text{of the two lines.} \\ \text{Write the second equation in} \\ \text{slope–intercept form.} \\ &2x+y&=&-3 & x−5y&=&5\\ & y &=& -2x -3 & -5y &=&-x+5 \\ &&&&\frac{-5y}{-5} &=& \frac{-x + 5}{-5}\\ &&&&y&=&\frac{1}{5}x-1\\\\ \text{Find the slope and intercept of each line.} & y &=& -2x-3 & y&=&\frac{1}{5}x-1 \\ &m &=& -2 & m &=& \frac{1}{5} \\&b&=&-3 &b&=&-1 \\ \text{Since the slopes are the same andy-intercepts} \\ \text{are different, the lines are parallel.}\end{array}\)
Um sistema de equações cujos gráficos são cruzados tem 1 solução e é consistente e independente.
Sem representar graficamente, determine o número de soluções e depois classifique o sistema de equações.
\(\begin{cases}{3x+2y=2} \\ {2x+y=1}\end{cases}\)
- Resposta
-
uma solução, consistente e independente
Sem representar graficamente, determine o número de soluções e depois classifique o sistema de equações.
\(\begin{cases}{x+4y=12} \\ {−x+y=3}\end{cases}\)
- Resposta
-
uma solução, consistente e independente
Sem representar graficamente, determine o número de soluções e depois classifique o sistema de equações. \(\begin{cases}{3x−2y=4} \\ {y=\frac{3}{2}x−2}\end{cases}\)
- Resposta
-
\(\begin{array}{lrrlrl} \text{We will compare the slopes and intercepts of the two lines.}& \begin{cases}{3x−2y} &=&{4} \\ {y}&=&{\frac{3}{2}x−2}\end{cases} \\ \text{Write the second equation in} \\ \text{slope–intercept form.} \\ &3x-2y&=&4 \\ & -2y &=& -3x +4 \\ &\frac{-2y}{-2} &=& \frac{-3x + 4}{-2}\\ &y&=&\frac{3}{2}x-2\\\\ \text{Find the slope and intercept of each line.} &y&=&\frac{3}{2}x-2\\ \text{Since the equations are the same, they have the same slope} \\ \text{and samey-intercept and so the lines are coincident.}\end{array}\)
Um sistema de equações cujos gráficos são linhas coincidentes tem infinitas soluções e é consistente e dependente.
Sem representar graficamente, determine o número de soluções e depois classifique o sistema de equações.
\(\begin{cases}{4x−5y=20} \\ {y=\frac{4}{5}x−4}\end{cases}\)
- Resposta
-
infinitas soluções, consistentes, dependentes
Sem representar graficamente, determine o número de soluções e depois classifique o sistema de equações.
\(\begin{cases}{ −2x−4y=8} \\ {y=−\frac{1}{2}x−2}\end{cases}\)
- Responda
-
infinitas soluções, consistentes, dependentes
Resolva aplicações de sistemas de equações por meio de gráficos
Usaremos a mesma estratégia de resolução de problemas que usamos em modelos matemáticos para configurar e resolver aplicações de sistemas de equações lineares. Modificaremos um pouco a estratégia aqui para torná-la apropriada para sistemas de equações.
- Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas.
- Identifique o que estamos procurando.
- Diga o que estamos procurando. Escolha variáveis para representar essas quantidades.
- Traduza em um sistema de equações.
- Resolva o sistema de equações usando boas técnicas de álgebra.
- Verifique a resposta do problema e verifique se faz sentido.
- Responda à pergunta com uma frase completa.
A etapa 5 é onde usaremos o método apresentado nesta seção. Vamos representar graficamente as equações e encontrar a solução.
Sondra está fazendo 10 litros de ponche com suco de frutas e refrigerante. O número de litros de suco de frutas é 4 vezes o número de litros de club soda. Quantos litros de suco de frutas e quantos litros de refrigerante Sondra precisa?
- Responda
-
Etapa 1. Leia o problema.
Etapa 2. Identifique o que estamos procurando.
Estamos procurando o número de litros de suco de frutas e o número de litros de club soda que a Sondra precisará.
Etapa 3. Diga o que estamos procurando. Escolha variáveis para representar essas quantidades.
Deixe f= número de litros de suco de frutas.
c= número de litros de club sodaEtapa 4. Traduza em um sistema de equações.
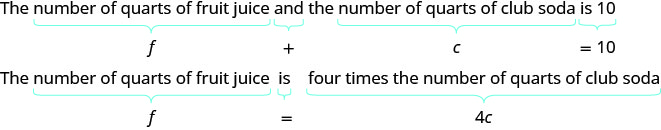
Agora temos o sistema. \(\begin{cases}{ f+c=10} \\ {f=4c}\end{cases}\)
Etapa 5. Resolva o sistema de equações usando boas técnicas de álgebra.
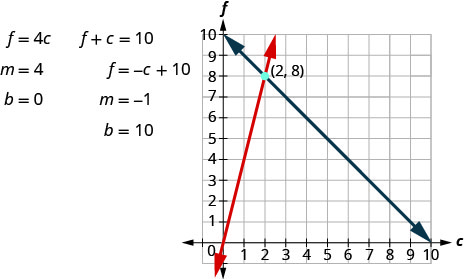
O ponto de interseção (2, 8) é a solução. Isso significa que Sondra precisa de 2 litros de refrigerante e 8 litros de suco de frutas.
Etapa 6. Verifique a resposta do problema e verifique se faz sentido.
Isso faz sentido no problema?
Sim, o número de litros de suco de frutas, 8, é 4 vezes o número de litros de refrigerante, 2.
Sim, 10 litros de ponche são 8 litros de suco de frutas mais 2 litros de refrigerante.
Etapa 7. Responda à pergunta com uma frase completa.
Sondra precisa de 8 litros de suco de frutas e 2 litros de refrigerante.
Manny está fazendo 12 litros de suco de laranja com concentrado e água. O número de litros de água é 3 vezes o número de litros de concentrado. Quantos litros de concentrado e quantos litros de água o Manny precisa?
- Responda
-
Manny precisa de 3 litros de suco concentrado e 9 litros de água.
Alisha está fazendo uma bebida de café de 18 onças que é feita com café moído e leite. O número de onças de café moído é 5 vezes maior do que o número de onças de leite. Quantas onças de café e quantas onças de leite a Alisha precisa?
- Responda
-
Alisha precisa de 15 onças de café e 3 onças de leite.
Acesse esses recursos on-line para obter instruções e práticas adicionais na resolução de sistemas de equações por meio de gráficos.
Conceitos chave
- Para resolver um sistema de equações lineares por meio de gráficos
- Faça um gráfico da primeira equação.
- Faça um gráfico da segunda equação no mesmo sistema de coordenadas retangulares.
- Determine se as linhas se cruzam, são paralelas ou são a mesma linha.
- Identifique a solução para o sistema.
Se as linhas se cruzarem, identifique o ponto de interseção. Verifique se é uma solução para ambas as equações. Essa é a solução para o sistema.
Se as linhas estiverem paralelas, o sistema não tem solução.
Se as linhas forem iguais, o sistema tem um número infinito de soluções. - Verifique a solução nas duas equações.
- Determine o número de soluções do gráfico de um sistema linear
- Determine o número de soluções de um sistema linear observando as inclinações e as interceptações
- Determine o número de soluções e como classificar um sistema de equações
- Estratégia de resolução de problemas para sistemas de equações lineares
- Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas.
- Identifique o que estamos procurando.
- Diga o que estamos procurando. Escolha variáveis para representar essas quantidades.
- Traduza em um sistema de equações.
- Resolva o sistema de equações usando boas técnicas de álgebra.
- Verifique a resposta do problema e verifique se faz sentido.
- Responda à pergunta com uma frase completa.
Glossário
- linhas coincidentes
- As linhas coincidentes são linhas que têm a mesma inclinação e o mesmo intercepto y.
- sistema consistente
- Um sistema consistente de equações é um sistema de equações com pelo menos uma solução.
- equações dependentes
- Duas equações dependem se todas as soluções de uma equação também forem soluções da outra equação.
- sistema inconsistente
- Um sistema de equações inconsistente é um sistema de equações sem solução.
- equações independentes
- Duas equações são independentes se tiverem soluções diferentes.
- soluções de um sistema de equações
- As soluções de um sistema de equações são os valores das variáveis que tornam todas as equações verdadeiras. Uma solução de um sistema de duas equações lineares é representada por um par ordenado (x, y).
- sistema de equações lineares
- Quando duas ou mais equações lineares são agrupadas, elas formam um sistema de equações lineares.


