Skip to main content
Global

1.8: Decimais

  1. Last updated
  2. Save as PDF
  • Page ID
    184472

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    objetivos de aprendizagem

    Ao final desta seção, você poderá:

    • Nomeie e escreva decimais
    • Números decimais arredondados
    • Adicione e subtraia números decimais
    • Multiplique e divida decimais
    • Converta números decimais, frações e porcentagens
    Nota

    Uma introdução mais completa aos tópicos abordados nesta seção pode ser encontrada no capítulo Pré-álgebra, Decimais.

    Nomear e escrever decimais

    Os decimais são outra forma de escrever a fração s cujos denominadores são potências de 10.

    \[\begin{array} {ll} {0.1 = \frac { 1 } { 10 }} &{0.1 \text { is "one tenth" }} \\ {0.01 = \frac { 1 } { 100 }} &{0.01 \text { is "one hundredth }} \\ {0.001 = \frac { 1 } { 1,000 }} &{0.001 \text { is "one thousandth }} \\ {0.0001 = \frac { 1 } { 10,000 }} &{0.0001 \text { is "one ten-thousandth" }} \end{array}\]

    Observe que “dez mil” é um número maior que um, mas “um dez mil” é um número menor que um. O “th” no final do nome indica que o número é menor que um.

    Quando nomeamos um número inteiro, o nome corresponde ao valor posicional com base nas potências de dez. Lemos 10.000 como “dez mil” e 10.000.000 como “dez milhões”. Da mesma forma, os nomes das casas decimais correspondem aos seus valores fracionários. A figura\(\PageIndex{1}\) mostra os nomes dos valores posicionais à esquerda e à direita do ponto decimal.

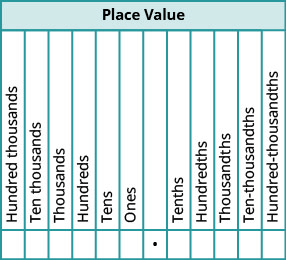
    Uma tabela é mostrada com o título Valor posicional. Da esquerda para a direita, a linha diz “Cem milhares”, “Dez milhares”, “Milhares”, “Centenas”, “Dezenas” e “Unidades”. Depois, há uma célula em branco e abaixo dela há um ponto decimal. À direita, as células lêem “Décimos”, “Centésimos”, “Milésimos”, “Dez milésimos” e “Cem milésimos”.
    Figura\(\PageIndex{1}\): O valor posicional dos números decimais é mostrado à esquerda e à direita do ponto decimal.
    Exercício\(\PageIndex{1}\)

    Dê um nome ao decimal\(4.3\).

    Resposta

    Uma tabela é fornecida com quatro etapas. Além disso, o número 4.3 é dado. A primeira etapa diz “Etapa 1. Nomeie o número à esquerda do ponto decimal.” À direita disso, observa-se que “4 está à esquerda do ponto decimal”. À direita, lê-se “quatro” seguido por um grande espaço em branco.A segunda etapa diz “Etapa 2. Escreva 'e' para o ponto decimal.” À direita, lê-se “quatro e” seguido por um espaço em branco.A terceira etapa diz “Etapa 3. Nomeie a parte do 'número' à direita do ponto decimal como se fosse um número inteiro.” À direita, lê-se “3 está à direita do ponto decimal”. À direita, lê-se “quatro e três” seguido por um espaço em branco.Finalmente, a última etapa diz “Etapa 4. Dê um nome à casa decimal.” À direita, lê-se “quatro e três décimos”.

    Exercício\(\PageIndex{2}\)

    Dê um nome ao decimal\(6.7\).

    Resposta

    seis e sete décimos

    Exercício\(\PageIndex{3}\)

    Dê um nome ao decimal\(5.8\).

    Resposta

    cinco e oito décimos

    Resumimos as etapas necessárias para nomear um decimal abaixo.

    DÊ UM NOME DECIMAL.
    1. Nomeie o número à esquerda do ponto decimal.
    2. Escreva “e” para o ponto decimal.
    3. Nomeie a parte do “número” à direita do ponto decimal como se fosse um número inteiro.
    4. Nomeie a casa decimal do último dígito.
    Exercício\(\PageIndex{4}\)

    Nomeie o decimal:\(−15.571\).

    Resposta
      \(−15.571\)
    Nomeie o número à esquerda do ponto decimal. menos quinze __________________________________
    Escreva “e” para o ponto decimal. menos quinze e ______________________________
    Nomeie o número à direita do ponto decimal. menos quinze e quinhentos e setenta e um __________
    O\(1\) está no milésimo lugar. menos quinze e quinhentos e setenta e um milésimos
    Exercício\(\PageIndex{5}\)

    Nomeie o decimal:\(−13.461\).

    Resposta

    menos treze e quatrocentos e sessenta e um milésimos

    Exercício\(\PageIndex{6}\)

    Nomeie o decimal:\(−2.053\).

    Resposta

    menos dois e cinquenta e três milésimos

    Quando escrevemos um cheque, escrevemos os números e o nome do número. Vamos ver como escrever o decimal a partir do nome.

    Exercício\(\PageIndex{7}\): How to Write decimals

    Escreva “quatorze e vinte e quatro milésimos” como decimal.

    Resposta

    Uma tabela é fornecida com quatro etapas. A primeira etapa diz “Etapa 1. Procure a obra 'e' — ela localiza o ponto decimal. Coloque um ponto decimal abaixo da palavra 'e'. Traduza as palavras antes de 'e' para o número inteiro e coloque-o à esquerda do ponto decimal.” À direita disso, temos as palavras “quatorze e vinte e quatro milésimos”. Abaixo dessa palavra, temos “quatorze e vinte e quatro milésimos” com a palavra “e” sublinhada. Abaixo dessa palavra, temos um pequeno espaço em branco separado de um espaço em branco maior por um ponto decimal. Abaixo disso, temos 14 no pequeno espaço em branco seguido pelo ponto decimal e pelo maior espaço em branco.A segunda etapa diz “Etapa 2. Marque o número de casas decimais necessárias à direita do ponto decimal anotando o valor posicional indicado pela última palavra.” À direita, lê-se “A última palavra é milésimos”. À direita, há o número 14 seguido por um ponto decimal e três pequenos espaços em branco. Sob os espaços em branco, as palavras “décimos”, “centésimos” e “milésimos” são escritas.A terceira etapa diz “Etapa 3. Traduza as palavras depois de 'e' para o número à direita do ponto decimal. Escreva o número nos espaços — colocando o dígito final no último lugar.” À direita disso, temos 14 seguido por um decimal seguido por um espaço em branco seguido por 2 e 4 nos outros dois espaços anteriormente em branco.Finalmente, a última etapa diz “Etapa 4. Preencha zeros para espaços vazios, conforme necessário.” À direita, lê-se “Zeros são necessários na décima posição”. À direita disso, temos 14 seguido por um ponto decimal seguido por 0, 2 e 4, respectivamente, nos espaços em branco. Abaixo disso, temos “quatorze e vinte e quatro milésimos estão escritos 14.024”.

    Exercício\(\PageIndex{8}\)

    Escreva como decimal: treze e sessenta e oito milésimos.

    Resposta

    13.068

    Exercício\(\PageIndex{9}\)

    Escreva como decimal: cinco e noventa e quatro milésimos.

    Resposta

    5.094

    Resumimos as etapas para escrever um decimal.

    ESCREVA UM DECIMAL.
    1. Procure a palavra “e” — ela localiza o ponto decimal.
      • Coloque um ponto decimal abaixo da palavra “e”. Traduza as palavras antes de “e” para o número inteiro e coloque-o à esquerda do ponto decimal.
      • Se não houver “e”, escreva um “0” com um ponto decimal à direita.
    2. Marque o número de casas decimais necessárias à direita do ponto decimal anotando o valor posicional indicado pela última palavra.
    3. Traduza as palavras depois de “e” para o número à direita do ponto decimal. Escreva o número nos espaços, colocando o dígito final no último lugar.
    4. Preencha zeros para os espaços reservados, conforme necessário.

    Decimais arredondados

    Arredondar decimais é muito parecido com arredondar números inteiros. Arredondaremos os decimais com um método baseado no que usamos para arredondar números inteiros.

    Exercício\(\PageIndex{10}\)

    Arredonde 18,379 para o centésimo mais próximo.

    Resposta

    Uma tabela é fornecida com quatro etapas. A primeira etapa diz “Etapa 1: localize o valor posicional fornecido e marque-o com uma seta”. À direita, temos o número 18.379; acima dele, estão as palavras centenas no lugar, que tem uma seta apontando para o 7.A segunda etapa diz “Etapa 2. Sublinhe o dígito à direita do valor posicional fornecido.” À direita disso, temos 18.379 com os 9 sublinhados.A terceira etapa diz “Etapa 3. Esse dígito é maior ou igual a 5? Abaixo está: “Sim: adicione 1 ao dígito no valor posicional fornecido”. Abaixo está: “Não: não altere o dígito no valor posicional fornecido”. À direita, está escrito “Porque 9 é maior ou igual a” À direita disso, temos o número 18.379 com o 9 marcado como “excluir” e o 7 marcado com “adicionar 1”.Finalmente, a última etapa diz “Etapa 4. Reescreva o número, removendo todos os dígitos à direita do dígito arredondado.” À direita disso, temos 18,38 seguido por “18,38 é 18,379 arredondado para o centésimo mais próximo”.

    Exercício\(\PageIndex{11}\)

    Arredondar para o centésimo mais próximo: 1,047.

    Resposta

    1,05

    Exercício\(\PageIndex{12}\)

    Arredondar para o centésimo mais próximo: 9,173.

    Resposta

    9,17

    Resumimos as etapas para arredondar um decimal aqui.

    DECIMAIS ARREDONDADOS.
    1. Localize o valor posicional fornecido e marque-o com uma seta.
    2. Sublinhe o dígito à direita do valor posicional.
    3. Esse dígito é maior ou igual a 5?
      • Sim — adicione 1 ao dígito no valor posicional fornecido.
      • Não — não altere o dígito no valor posicional fornecido.
    4. Reescreva o número, excluindo todos os dígitos à direita do dígito arredondado.
    Exercício\(\PageIndex{13}\)

    Arredonde 18.379 para o mais próximo

    1. décimo
    2. número inteiro.
    Resposta

    Rodada 18.379

    1. até o décimo mais próximo

    Localize o décimo lugar com uma seta. .
    Sublinhe o dígito à direita do valor posicional fornecido. .
    Como 7 é maior ou igual a 5, adicione 1 ao 3. .
    Reescreva o número, excluindo todos os dígitos à direita do dígito arredondado. .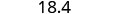
    Observe que os dígitos excluídos NÃO foram substituídos por zeros. Então, 18,379 arredondado para o décimo mais próximo é 18,4.


    2. para o número inteiro mais próximo
    Localize o único lugar com uma flecha. .
    Sublinhe o dígito à direita do valor posicional fornecido. .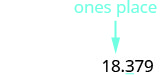
    Como 3 não é maior ou igual a 5, não adicione 1 ao 8. .
    Reescreva o número, excluindo todos os dígitos à direita do dígito arredondado. .
      Portanto, 18,379 arredondado para o número inteiro mais próximo é 18.
    Exercício\(\PageIndex{14}\)

    Arredonde 6,582 para o mais próximo

    1. centésimo
    2. décimo
    3. número inteiro.
    Resposta
    1. 6,58
    2. 6.6
    3. 7
    Exercício\(\PageIndex{15}\)

    Arredonde 15.2175 para o mais próximo

    1. milésimo
    2. centésimo
    3. décimo.
    Resposta
    1. 15.218
    2. 15,22
    3. 15.2

    Adicionar e subtrair números decimais

    Para somar ou subtrair decimais, alinhamos os pontos decimais. Ao alinhar os pontos decimais dessa forma, podemos somar ou subtrair os valores posicionais correspondentes. Em seguida, adicionamos ou subtraímos os números como se fossem números inteiros e colocamos o ponto decimal na soma.

    ADICIONE OU SUBTRAIA NÚMEROS DECIMAIS.
    1. Escreva os números para que os pontos decimais se alinhem verticalmente.
    2. Use zeros como espaços reservados, conforme necessário.
    3. Adicione ou subtraia os números como se fossem números inteiros. Em seguida, coloque o ponto decimal na resposta abaixo dos pontos decimais nos números fornecidos.
    Exercício\(\PageIndex{16}\)

    Adicionar:\(23.5+41.38\).

    Resposta

    \[\text{Write the numbers so that the decimal points line up vertically.} \quad \begin{array} {r} { 23.50 } \\ { + 41.38 } \\ \hline \end{array}\]
    \[\text{Put 0 as a placeholder after the 5 in 23.5. Remember, } \frac{5}{10} = \frac{50}{100}, \text{ so } 0.5 = 0.50 \quad \begin{array} {r} { 23.50 } \\ { + 41.38 } \\ \hline \end{array}\]
    \[\text{Add the numbers as if they were whole numbers . Then place the decimal point in the sum.} \quad \begin{array} {r} { 23.50 } \\ { + 41.38 } \\ \hline 64.88 \end{array}\]

    Exercício\(\PageIndex{17}\)

    Adicionar:\(4.8+11.69\).

    Resposta

    \(16.49\)

    Exercício\(\PageIndex{18}\)

    Adicionar:\(5.123+18.47\).

    Resposta

    \(23.593\)

    Exercício\(\PageIndex{19}\)

    Subtraia:\(20−14.65\).

    Resposta

    \[\begin{array} {ll} {\text{Write the numbers so that the decimal points line up vertically.}} &{ \begin{align} {20 - 14.65} \\ {20.} \\ {-14.65} \\ \hline \end{align}} \\ {\text{Remember, 20 is a whole number, so place the decimal point after the 0.}} &{} \end{array}\]
    \[\begin{array} {ll} {\text{Put zeros to the right as placeholders.}} &{ \begin{align} {20.00} \\ {-14.65} \\ \hline \end{align}} \end{array}\]
    \[\begin{array} {ll} {\text{Write the numbers so that the decimal points line up vertically.}} &{ \begin{align} {\tiny{9} \quad \tiny{9}\qquad} \\ {\small{1} \not{\small{10}} \not{\small10}\not{\small10}}\\ {\not{2}\not{0.}\not{0}\not{0}} \\ {-14.65} \\ \hline \\{5.35} \end{align}} \end{array}\]

    Exercício\(\PageIndex{20}\)

    Subtraia:\(10−9.58\).

    Resposta

    0,42

    Exercício\(\PageIndex{21}\)

    Subtraia:\(50−37.42\).

    Resposta

    12,58

    Multiplique e divida números decimais

    Multiplicar decimais é muito parecido com multiplicar números inteiros — só precisamos determinar onde colocar o ponto decimal. O procedimento para multiplicar decimais fará sentido se primeiro os convertermos em frações e depois multiplicarmos.

    Então, vamos ver o que obteríamos como produto dos decimais convertendo-os primeiro em frações. Faremos dois exemplos lado a lado. Procure um padrão!

      .

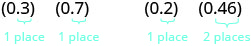    Converta em frações.    		 .
    Multiplique. .
    Converta em decimais. .
    Tabela\(\PageIndex{1}\)

    Observe que, no primeiro exemplo, multiplicamos dois números, cada um com um dígito após o ponto decimal e o produto tinha duas casas decimais. No segundo exemplo, multiplicamos um número com uma casa decimal por um número com duas casas decimais e o produto tinha três casas decimais.

    Multiplicamos os números da mesma forma que fazemos com números inteiros, ignorando temporariamente o ponto decimal. Em seguida, contamos o número de pontos decimais nos fatores e essa soma nos diz o número de casas decimais no produto.

    As regras para multiplicar números positivos e negativos também se aplicam aos decimais, é claro!

    Ao multiplicar dois números,

    • se seus sinais forem os mesmos, o produto é positivo.
    • se seus sinais forem diferentes, o produto é negativo.

    Quando multiplicamos decimais assinados, primeiro determinamos o sinal do produto e depois multiplicamos como se os números fossem positivos. Por fim, escrevemos o produto com o sinal apropriado.

    MULTIPLIQUE NÚMEROS DECIMAIS.
    1. Determine o sinal do produto.
    2. Escreva em formato vertical, alinhando os números à direita. Multiplique os números como se fossem números inteiros, ignorando temporariamente os pontos decimais.
    3. Coloque o ponto decimal. O número de casas decimais no produto é a soma do número de casas decimais nos fatores.
    4. Escreva o produto com o sinal apropriado.
    Exercício\(\PageIndex{22}\)

    Multiplique:\((−3.9)(4.075)\).

    Resposta
      \((−3.9)(4.075)\)
    Os sinais são diferentes. O produto será negativo.  
    Escreva em formato vertical, alinhando os números à direita. .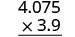
    Multiplique. .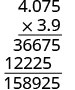
    Adicione o número de casas decimais nos fatores\((1 + 3)\).

    .
    Coloque o ponto decimal a 4 casas da direita.    		 .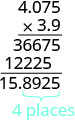
    Os sinais são diferentes, então o produto é negativo. \((−3.9)(4.075) = −15.8925\)
    Exercício\(\PageIndex{23}\)

    Multiplique:\(−4.5(6.107)\).

    Resposta

    \(−27.4815\)

    Exercício\(\PageIndex{24}\)

    Multiplique: −10,79 (8,12).

    Resposta

    \(−87.6148\)

    Em muitas de suas outras aulas, especialmente nas ciências, você multiplicará decimais por potências de 10 (10, 100, 1000, etc.). Se você multiplicar alguns produtos no papel, poderá notar um padrão relacionando o número de zeros na potência de 10 ao número de casas decimais. Movemos o ponto decimal para a direita para obter o produto.

    MULTIPLIQUE UM DECIMAL POR UMA POTÊNCIA DE DEZ.
    1. Mova o ponto decimal para a direita com o mesmo número de casas que o número de zeros na potência de 10.
    2. Adicione zeros no final do número conforme necessário.
    Exercício\(\PageIndex{25}\)

    Multiplique 5,63

    1. por 10
    2. por 100
    3. por 1.000.
    Resposta

    Ao observar o número de zeros no múltiplo de dez, vemos o número de casas que precisamos mover o decimal para a direita.

    ⓐ

      \(5.63(10)\)
    Há 1 zero em 10, então mova o ponto decimal 1 casa para a direita. .

    ⓑ

      \(5.63(100)\)
    Há 2 zeros em 100, então mova o ponto decimal 2 casas para a direita. .

    ⓒ

       
    Há 3 zeros em 1.000, então mova o ponto decimal 3 casas para a direita. .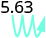
    Um zero deve ser adicionado no final. .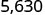
    Exercício\(\PageIndex{26}\)

    Multiplique 2,58

    1. por 10
    2. por 100
    3. por 1.000.
    Resposta
    1. 25,8
    2. 258
    3. 2.580
    Exercício\(\PageIndex{27}\)

    Multiplique 14,2

    1. por 10
    2. por 100
    3. por 1.000.
    Resposta
    1. 142
    2. 1.420
    3. 14.200

    Assim como na multiplicação, a divisão de decimais é muito parecida com a divisão de números inteiros. Só precisamos descobrir onde o ponto decimal deve ser colocado.

    Para dividir decimais, determine por qual potência de 10 multiplicar o denominador para torná-lo um número inteiro. Em seguida, multiplique o numerador pela mesma potência de 10. Por causa da propriedade de frações equivalentes, não alteramos o valor da fração! O efeito é mover os pontos decimais no numerador e no denominador com o mesmo número de casas para a direita. Por exemplo:

    \[\begin{array} { c } { \frac { 0.8 } { 0.4 } } \\ { \frac { 0.8 ( 10 ) } { 0.4 ( 10 ) } } \\ { \frac { 8 } { 4 } } \end{array}\]

    Também usamos as regras para dividir números positivos e negativos com decimais. Ao dividir decimais assinados, primeiro determine o sinal do quociente e depois divida como se os números fossem positivos. Finalmente, escreva o quociente com o sinal apropriado.

    Nós revisamos a notação e o vocabulário para divisão:

    \[\begin{array} {ll} {} &{\underset{\text{quotient}}{c}} \\ {\underset{\text{dividend}}{a} \div \underset{\text{divisor}}{b} = \underset{\text{quotient}}{c}} & {\underset{\text{divisor}}{b})\overline{\underset{\text{dividend}}{a}}} \end{array}\]

    Escreveremos as etapas a serem seguidas ao dividir os decimais, para facilitar a referência.

    DIVIDA NÚMEROS DECIMAIS.
    1. Determine o sinal do quociente.
    2. Transforme o divisor em um número inteiro “movendo” o ponto decimal totalmente para a direita. “Mova” o ponto decimal no dividendo pelo mesmo número de casas, adicionando zeros conforme necessário.
    3. Divida. Coloque o ponto decimal no quociente acima do ponto decimal no dividendo.
    4. Escreva o quociente com o sinal apropriado.
    Exercício\(\PageIndex{28}\)

    Divida:\(−25.65\div (−0.06)\).

    Resposta

    Lembre-se de que você pode “mover” os decimais no divisor e no dividendo por causa da Propriedade de Frações Equivalentes.

      \(−25.65\div (−0.06)\)
    Os sinais são os mesmos. O quociente é positivo.
    Transforme o divisor em um número inteiro “movendo” o ponto decimal totalmente para a direita.  
    “Mova” o ponto decimal no dividendo pelo mesmo número de casas. .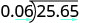
    Divida.
    Coloque o ponto decimal no quociente acima do ponto decimal no dividendo.    		 .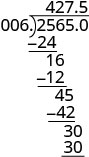
    Escreva o quociente com o sinal apropriado. \(−25.65\div (−0.06) = 427.5\)
    Exercício\(\PageIndex{29}\)

    Divida:\(−23.492\div (−0.04)\).

    Resposta

    687,3

    Exercício\(\PageIndex{30}\)

    Divida:\(−4.11\div(−0.12)\).

    Resposta

    34,25

    Uma aplicação comum de dividir números inteiros em decimais é quando queremos encontrar o preço de um item que é vendido como parte de um pacote múltiplo. Por exemplo, suponha que um caso de 24 garrafas de água custe\($3.99\). Para encontrar o preço de uma garrafa de água, dividiríamos\($3.99\) por 24. Mostramos essa divisão no Exercício\(\PageIndex{31}\). Nos cálculos com dinheiro, arredondaremos a resposta para o centésimo mais próximo.

    Exercício\(\PageIndex{31}\)

    Divida:\($3.99\div 24\).

    Resposta
    .99 dividido por 24 é dado. Um problema de divisão longa é configurado com 24 dividindo 3,99. Uma tabela é fornecida com as instruções à esquerda e as etapas matemáticas à direita. A primeira etapa diz “Coloque o ponto decimal no quociente acima do ponto decimal no dividendo. Divida como de costume. Quando vamos parar? Como essa divisão envolve dinheiro, nós a arredondamos para o centésimo mais próximo. Para fazer isso, devemos levar a divisão até o milésimo lugar.” À direita disso, temos um longo problema de divisão configurado com 24 dividindo 3.990. O quociente é dado como 0,166. Para mostrar o trabalho, abaixo de 3.990, lê-se 24, linha horizontal sólida, 159, 144, linha horizontal sólida, 150, 144, linha horizontal sólida e, finalmente, 6. A quinta etapa diz “Arredonde para o centavo mais próximo”. À direita disso, temos $0.166 é aproximadamente igual a $0.17 e, portanto, >.99 dividido por 24 é $0.17.” >
      \($3.99\div 24\)
    Coloque o ponto decimal no quociente acima do ponto decimal no dividendo.  
    Divida como de costume.
    Quando vamos parar? Como essa divisão envolve dinheiro, nós a arredondamos para o centésimo mais próximo (centésimo). Para fazer isso, devemos levar a divisão até o milésimo lugar.    		 .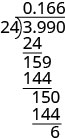
    Arredonde para o centavo mais próximo. \($0.166\approx $0.17\)
    \($3.99\div 2\approx $0.17\)
    Exercício\(\PageIndex{32}\)

    Divida:\($6.99\div 36\).

    Resposta

    \($0.19\)

    Exercício\(\PageIndex{33}\)

    Divida:\($4.99\div 12\).

    Resposta

    \($0.42\)

    Converta números decimais, frações e porcentagens

    Convertemos decimais em frações identificando o valor posicional do último dígito (mais à direita). No decimal 0,03, o 3 está na casa dos centésimos, então 100 é o denominador da fração equivalente a 0,03.

    \[00.03 = \frac { 3 } { 100 }\]

    Observe que, quando o número à esquerda do decimal é zero, obtemos uma fração cujo numerador é menor que seu denominador. Frações como essa são chamadas de frações próprias.

    As etapas a serem seguidas para converter um decimal em uma fração estão resumidas na caixa de procedimento.

    CONVERTA UM DECIMAL EM UMA FRAÇÃO ADEQUADA.
    1. Determine o valor posicional do dígito final.
    2. Escreva a fração.
      • numerador—os “números” à direita do ponto decimal
      • denominador — o valor posicional correspondente ao dígito final
    Exercício\(\PageIndex{34}\)

    Escreva 0,374 como uma fração.

    Resposta
      0,374
    Determine o valor posicional do dígito final. .

    Escreva a fração para 0,374:

    • O numerador é 374.
    • O denominador é 1.000.
    		 \(\dfrac{374}{1000}\)
    Simplifique a fração. \(\dfrac{2\cdot 187}{2\cdot 500}\)
    Divida os fatores comuns. \(\dfrac{187}{500}\)
    então,\(0.374=\dfrac{187}{500}\)

    Você notou que o número de zeros no denominador de\(\dfrac{374}{1000}\) é o mesmo que o número de casas decimais em 0,374?

    Exercício\(\PageIndex{35}\)

    Escreva 0,234 como uma fração.

    Resposta

    \(\dfrac{117}{500}\)

    Exercício\(\PageIndex{36}\)

    Escreva 0,024 como uma fração.

    Resposta

    \(\dfrac{3}{125}\)

    Aprendemos a converter decimais em frações. Agora faremos o inverso: converter frações em decimais. Lembre-se de que a barra de fração significa divisão. Então\(\dfrac{4}{5}\) pode ser escrito\(4\div 5\) ou\(5)\overline{4}\). Isso leva ao seguinte método para converter uma fração em decimal.

    CONVERTA UMA FRAÇÃO EM UM DECIMAL.

    Para converter uma fração em decimal, divida o numerador da fração pelo denominador da fração.

    Exercício\(\PageIndex{37}\)

    Escreva\(-\dfrac{5}{8}\) como decimal.

    Resposta

    Como uma barra fracionária significa divisão, começamos escrevendo\(\dfrac{5}{8}\) como\(8)\overline{5}\). Agora divida.

    Esse é um problema de divisão longa com 8 dividindo 5.000 e 0,625 como quociente. Abaixo de 5.000, temos 48, uma linha horizontal sólida, 20, 16, uma linha horizontal sólida, 40, 40 e uma linha horizontal final. Então, cinco oitavos é igual a 0,625.

    Exercício\(\PageIndex{38}\)

    Escreva\(-\dfrac{7}{8}\) como decimal.

    Resposta

    −0,875

    Exercício\(\PageIndex{39}\)

    Escreva\(-\dfrac{3}{8}\) como decimal.

    Resposta

    −0,375

    Quando dividimos, nem sempre obteremos um restante zero. Às vezes, o quociente termina com um decimal que se repete. Um decimal repetido é um decimal no qual o último dígito ou grupo de dígitos se repete indefinidamente. Uma barra é colocada sobre o bloco repetido de dígitos para indicar que ele se repete.

    REPETIÇÃO DECIMAL

    Um decimal repetido é um decimal no qual o último dígito ou grupo de dígitos se repete indefinidamente.

    Uma barra é colocada sobre o bloco repetido de dígitos para indicar que ele se repete.

    Exercício\(\PageIndex{40}\)

    Escreva\(\dfrac{43}{22}\) como decimal.

    Resposta

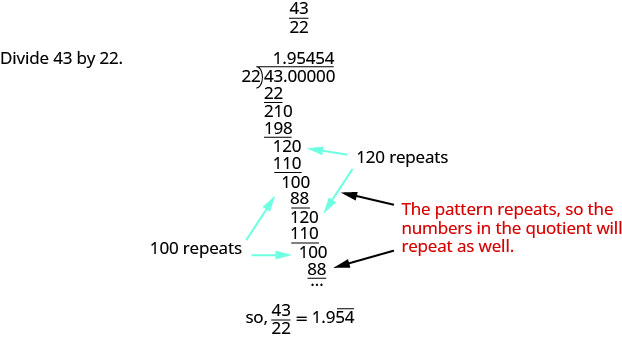
    O número 43/22 é dado. A direção é dada para “Divida 43 por 22”. Um problema de divisão longa é dado com 22 dividindo 43.00000 com 1.95454 como quociente. Abaixo de 43.00000 temos 22, uma linha horizontal sólida, 210, 198, uma linha horizontal sólida, 120, 110, uma linha horizontal, 100, 88, uma linha horizontal sólida, 120, 110, uma linha horizontal sólida, 100, 88, uma linha horizontal sólida e, em seguida, três pontos. Note-se que as 120 se repetem e que as 100 se repetem. Isso é explicado ainda mais como “O padrão se repete, então os números no quociente também se repetirão. No final, recebemos a afirmação de que 43/22 é igual a 1,954 com uma pequena linha horizontal sobre a 54.

    Exercício\(\PageIndex{41}\)

    Escreva\(\dfrac{27}{11}\) como decimal.

    Resposta

    \(2.\overline{45}\)

    Exercício\(\PageIndex{42}\)

    Escreva\(\dfrac{51}{22}\) como decimal.

    Resposta

    \(2.3\overline{18}\)

    Às vezes, talvez precisemos simplificar expressões com frações e decimais juntos.

    Exercício\(\PageIndex{43}\)

    Simplifique:\(\dfrac{7}{8}+6.4\).

    Resposta

    Primeiro, devemos alterar um número para que ambos estejam na mesma forma. Podemos mudar a fração para um decimal ou mudar o decimal para uma fração. Normalmente, é mais fácil alterar a fração para um decimal.

        \(\dfrac{7}{8}+6.4\)
    \(\dfrac{7}{8}\)Mude para um decimal. .  
    Adicionar.   \(0.875+6.4\)
        \(7.275\)
        Então,\(\dfrac{7}{8}+6.4 = 7.275\)
    Exercício\(\PageIndex{44}\)

    Simplifique:\(\dfrac{3}{8}+4.9\).

    Resposta

    \(5.275\)

    Exercício\(\PageIndex{45}\)

    Simplifique:\(5.7 + \dfrac{13}{20}\).

    Resposta

    \(6.35\)

    Uma porcentagem é uma proporção cujo denominador é 100. Porcentagem significa por cem. Usamos o símbolo de porcentagem,%, para mostrar a porcentagem.

    PORCENTAGEM

    Uma porcentagem é uma proporção cujo denominador é 100.

    Como uma porcentagem é uma proporção, ela pode ser facilmente expressa como uma fração. Porcentagem significa por 100, então o denominador da fração é 100. Em seguida, alteramos a fração para um decimal dividindo o numerador pelo denominador.

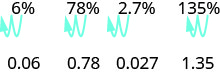
    \[\begin{array} {llll} {} &{\text{6%}} &{\text{78%}} &{\text{135%}} \\ {\text { Write as a ratio with denominator } 100. } &{\dfrac{6}{100}} &{\dfrac{78}{100}} &{\dfrac{135}{100}} \\ { \text { Change the fraction to a decimal by dividing}} &{0.06} &{0.78} &{1.35}\\ {\text{the numerator by the denominator.}} &{} &{} &{} \end{array}\]

    Você vê o padrão? Para converter um número percentual em um número decimal, movemos o ponto decimal duas casas para a esquerda.

    A primeira parte desta figura mostra 6% com uma seta desenhada entre o 6 e o sinal de porcentagem no espaço à esquerda de 6 e depois no espaço mais à esquerda desse espaço. Abaixo disso, o número 0,06 é dado. A segunda parte desta figura mostra 78% com uma seta desenhada entre o 8 e o sinal de porcentagem para o espaço entre o 7 e o 8 e depois para o espaço à esquerda do 7. Abaixo disso, o número 0,78 é dado. A terceira parte desta figura mostra 2,7% com uma seta desenhada do ponto decimal para o espaço à esquerda do 2 e depois para o espaço mais à esquerda desse espaço. Abaixo disso, o número 0,027 é dado. A quarta parte desta figura mostra 135% com uma seta desenhada entre o 5 e o sinal de porcentagem para o espaço entre 3 e 5 e depois para o espaço entre 1 e 3. Abaixo disso, o número 1,35 é dado.
    Figura\(\PageIndex{2}\)
    Exercício\(\PageIndex{46}\)

    Converta cada porcentagem em um decimal:

    1. 62%
    2. 135%
    3. 35,7%.
    Resposta
    1.  
      .
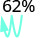
    Mova o ponto decimal duas casas para a esquerda. 0,62
    2.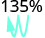  
      .
    Mova o ponto decimal duas casas para a esquerda. 1,35
    3.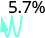  
      .
    Mova o ponto decimal duas casas para a esquerda. 0,057
    Exercício\(\PageIndex{47}\)

    Converta cada porcentagem em um decimal:

    1. 9%
    2. 87%
    3. 3,9%.
    Resposta
    1. 0,09
    2. 0,87
    3. 0,039
    Exercício\(\PageIndex{48}\)

    Converta cada porcentagem em um decimal:

    1. 3%
    2. 91%
    3. 8,3%.
    Resposta
    1. 0,03
    2. 0,91
    3. 0,083

    A conversão de um decimal em porcentagem faz sentido se nos lembrarmos da definição de porcentagem e tivermos em mente o valor posicional.

    Para converter um decimal em um percentual, lembre-se de que porcentagem significa por cem. Se mudarmos o decimal para uma fração cujo denominador é 100, é fácil alterar essa fração para um percentual.

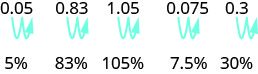
    \[\begin{array} {llll} {} &{0.83} &{1.05} &{0.075} \\ {\text {Write as a fraction }} &{\frac{83}{100}} &{\small{1}\frac{5}{100}} &{\frac{75}{1000}} \\ { \text {The denominator is 100.}} &{} &{\frac{105}{100}} &{\frac{7.5}{100}}\\ {\text{Write the ratio as a percent.}} &{\text{83%}} &{\text{105%}} &{\text{7.5%}} \end{array}\]

    Reconhece o padrão? Para converter um decimal em um percentual, movemos o ponto decimal duas casas para a direita e, em seguida, adicionamos o sinal de porcentagem.

    A primeira parte desta figura mostra 0,05 com uma seta desenhada do ponto decimal para o espaço entre 0 e 5 e depois para o espaço após 5. Abaixo disso, o número 5% é dado. A segunda parte desta figura mostra 0,83 com uma seta desenhada do ponto decimal para o espaço entre 8 e 3 e depois para o espaço após 3. Abaixo disso, o número 83% é dado. A terceira parte desta figura mostra 1,05 com uma seta desenhada do ponto decimal para o espaço entre 0 e 5 e depois para o espaço após 5. Abaixo disso, o número 105% é dado. A quarta parte desta figura mostra 0,075 com uma seta desenhada do ponto decimal para o espaço entre 0 e 7 e depois para o espaço entre 7 e 5. Abaixo disso, o número 7,5% é dado. A quinta parte desta figura mostra 0,3 com uma seta desenhada do ponto decimal para o espaço após 3 e depois para o espaço mais à direita desse 3. Abaixo disso, o número 30% é dado.
    Figura\(\PageIndex{3}\)
    Exercício\(\PageIndex{49}\)

    Converta cada decimal em uma porcentagem:

    1. 0,51
    2. 1,25
    3. 0,093.
    Resposta
    1.  
      .
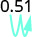
    Mova o ponto decimal duas casas para a direita. \(51%\)
    2.  
      .
    Mova o ponto decimal duas casas para a direita. \(125%\)
    3.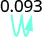  
      .
    Mova o ponto decimal duas casas para a direita. \(9.3%\)
    Exercício\(\PageIndex{50}\)

    Converta cada decimal em uma porcentagem:

    1. 0,17
    2. 1,75
    3. 0,0825
    Resposta
    1. 17%
    2. 175%
    3. 8,25%
    Exercício\(\PageIndex{51}\)

    Converta cada decimal em uma porcentagem:

    1. 0,41
    2. 2,25
    3. 0,0925.
    Resposta
    1. 41%
    2. 25%
    3. 9,25%

    Conceitos-chave

    • Nomear um decimal
      1. Nomeie o número à esquerda do ponto decimal.
      2. Escreva” e” para o ponto decimal.
      3. Nomeie a parte do “número” à direita do ponto decimal como se fosse um número inteiro.
      4. Nomeie a casa decimal do último dígito.
    • Escreva um decimal
      1. Procure a palavra “e” — ela localiza o ponto decimal. Coloque um ponto decimal abaixo da palavra “e”. Traduza as palavras antes de 'e' para o número inteiro e posicione-as à esquerda do ponto decimal. Se não houver “e”, escreva um “0” com um ponto decimal à direita.
      2. Marque o número de casas decimais necessárias à direita do ponto decimal anotando o valor posicional indicado pela última palavra.
      3. Traduza as palavras depois de 'e' para o número à direita do ponto decimal. Escreva o número nos espaços, colocando o dígito final no último lugar.
      4. Preencha zeros para os espaços reservados, conforme necessário.
    • Arredondar um decimal
      1. Localize o valor posicional fornecido e marque-o com uma seta.
      2. Sublinhe o dígito à direita do valor posicional.
      3. Esse dígito é maior ou igual a 5? Sim — adicione 1 ao dígito no valor posicional fornecido. Não — não altere o dígito no valor posicional fornecido.
      4. Reescreva o número, excluindo todos os dígitos à direita do dígito arredondado.
    • Adicionar ou subtrair números decimais
      1. Escreva os números para que os pontos decimais se alinhem verticalmente.
      2. Use zeros como espaços reservados, conforme necessário.
      3. Adicione ou subtraia os números como se fossem números inteiros. Em seguida, coloque o decimal na resposta abaixo dos pontos decimais nos números fornecidos.
    • Multiplique números decimais
      1. Determine o sinal do produto.
      2. Escreva em formato vertical, alinhando os números à direita. Multiplique os números como se fossem números inteiros, ignorando temporariamente os pontos decimais.
      3. Coloque o ponto decimal. O número de casas decimais no produto é a soma das casas decimais nos fatores.
      4. Escreva o produto com o sinal apropriado.
    • Multiplique um decimal por uma potência de dez
      1. Mova o ponto decimal para a direita com o mesmo número de casas que o número de zeros na potência de 10.
      2. Adicione zeros no final do número conforme necessário.
    • Divida números decimais
      1. Determine o sinal do quociente.
      2. Transforme o divisor em um número inteiro “movendo” o ponto decimal totalmente para a direita. “Mova” o ponto decimal no dividendo pelo mesmo número de casas - adicionando zeros conforme necessário.
      3. Divida. Coloque o ponto decimal no quociente acima do ponto decimal no dividendo.
      4. Escreva o quociente com o sinal apropriado.
    • Converter um decimal em uma fração própria
      1. Determine o valor posicional do dígito final.
      2. Escreva a fração: numerador — os 'números' à direita do ponto decimal; denominador — o valor posicional correspondente ao dígito final.
    • Converta uma fração em decimal Divida o numerador da fração pelo denominador.