13.4: Séries e suas notações
- Page ID
- 186586
- Use a notação de soma.
- Use a fórmula para a soma dos primeiros\(n\) termos de uma série aritmética.
- Use a fórmula para a soma dos primeiros\(n\) termos de uma série geométrica.
- Use a fórmula para a soma de uma série geométrica infinita.
- Resolva problemas de anuidade.
Um casal decide abrir um fundo universitário para a filha. Eles planejam investir\($50\) no fundo todos os meses. O fundo paga juros\(6\%\) anuais, compostos mensalmente. Quanto dinheiro eles terão economizado quando sua filha estiver pronta para começar a faculdade em\(6\) anos? Nesta seção, aprenderemos como responder a essa pergunta. Para fazer isso, precisamos considerar a quantidade de dinheiro investida e a quantidade de juros auferidos.
Usando a notação de soma
Para encontrar a quantia total de dinheiro no fundo da faculdade e a soma dos valores depositados, precisamos adicionar os valores depositados a cada mês e os valores ganhos mensalmente. A soma dos termos de uma sequência é chamada de série. Considere, por exemplo, a série a seguir.
\(3+7+11+15+19+ \ldots \nonumber \)
A soma\(n^{th}\) parcial de uma série é a soma de um número finito de termos consecutivos começando com o primeiro termo. A notação\(S_n\) representa a soma parcial.
\[\begin{align} S_1 &= 3 \nonumber \\ S_2 &= 3+7=10 \nonumber \\ S_3 &= 3+7+11=21 \nonumber \\ S_4 &= 3+7+11+15 =36 \nonumber \end{align} \nonumber\]
A notação de soma é usada para representar séries. A notação somatória é frequentemente conhecida como notação sigma porque usa a letra maiúscula grega sigma\(\sum\),, para representar a soma. A notação de soma inclui uma fórmula explícita e especifica o primeiro e o último termos da série. Uma fórmula explícita para cada termo da série é dada à direita do sigma. Uma variável chamada índice de soma está escrita abaixo do sigma. O índice de soma é definido como igual ao limite inferior da soma, que é o número usado para gerar o primeiro termo da série. O número acima do sigma, chamado limite superior da soma, é o número usado para gerar o último termo de uma série.
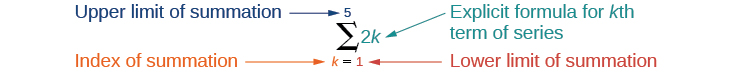
Se interpretarmos a notação dada, vemos que ela solicita que encontremos a soma dos termos na série\(a_k=2k\) por\(k=1\) meio\(k=5\). Podemos começar substituindo os termos\(k\) e listando os termos desta série.
\[\begin{align}a_1 &=2(1)=2 \nonumber \\ a_2 &=2(2)=4 \nonumber \\ a_3 &= 2(3)=6 \nonumber \\ a_4 &= 2(4)=8 \nonumber \\ a_5 &= 2(5)=10 \nonumber \end{align} \nonumber\]
Podemos encontrar a soma da série adicionando os termos:
\[\sum_{k=1}^{5}2k=2+4+6+8+10=30 \nonumber\]
A soma dos primeiros\(n\) termos de uma série pode ser expressa em notação de soma da seguinte forma:
\[\sum_{k=1}^{n}a_k\]
Essa notação nos diz para encontrar a soma de\(a_k\) de\(k=1\) até\(k=n\).
\(k\)é chamado de índice de soma,\(1\) é o limite inferior da soma e\(n\) é o limite superior da soma.
Não. O limite inferior da soma pode ser qualquer número, mas\(1\) é usado com frequência. Veremos exemplos com limites mais baixos de soma diferentes de\(1\).
- Identifique o limite inferior da soma.
- Identifique o limite superior da soma.
- Substitua cada valor\(k\) do limite inferior pelo limite superior na fórmula.
- Adicione para encontrar a soma.
Avalie
\(\sum_{k=3}^{7}k^2\)
Solução
De acordo com a notação, o limite inferior da soma é\(3\) e o limite superior é\(7\). Então, precisamos encontrar a soma de\(k^2\) de\(k=3\) até\(k=7\). Encontramos os termos da série substituindo\(k=3, 4, 5, 6,\) e\(7\) entrando na função\(k^2\). Nós adicionamos os termos para encontrar a soma.
\[\begin{align}\sum_{k=3}^{7}k^2 &= 3^2+4^2+5^2+6^2+7^2 \nonumber \\[4pt] &= 9+16+25+36+49 \nonumber \\[4pt] &= 135 \nonumber \end{align} \nonumber\]
Avalie
\(\sum_{k=2}^{5}(3k–1)\)
- Responda
-
\(38\)
Usando a fórmula para séries aritméticas
Assim como estudamos tipos especiais de sequências, veremos tipos especiais de séries. Lembre-se de que uma sequência aritmética é uma sequência na qual a diferença entre quaisquer dois termos consecutivos é a diferença comum,\(d\). A soma dos termos de uma sequência aritmética é chamada de série aritmética. Podemos escrever a soma dos primeiros\(n\) termos de uma série aritmética como:
\[S_n=a_1+(a_1+d)+(a_1+2d)+...+(a_n–d)+a_n. \nonumber \]
Também podemos reverter a ordem dos termos e escrever a soma como
\[S_n=a_n+(a_n–d)+(a_n–2d)+...+(a_1+d)+a_1. \nonumber\]
Se somarmos essas duas expressões para a soma dos primeiros\(n\) termos de uma série aritmética, podemos derivar uma fórmula para a soma dos primeiros\(n\) termos de qualquer série aritmética.
\[S_n=a_1+(a_1+d)+(a_1+2d)+...+(a_n–d)+a_n \nonumber\]
\[\underline{+S_n=a_n+(a_n–d)+(a_n–2d)+...+(a_1+d)+a_1} \nonumber\]
\[2S_n=(a_1+a_n)+(a_1+a_n)+...+(a_1+a_n) \nonumber\]
Como existem\(n\) termos na série, podemos simplificar essa soma para
\[2S_n=n(a_1+a_n). \nonumber \]
Dividimos por\(2\) para encontrar a fórmula para a soma dos primeiros\(n\) termos de uma série aritmética.
\[S_n=\dfrac{n(a_1+a_n)}{2} \nonumber \]
Uma série aritmética é a soma dos termos de uma sequência aritmética. A fórmula para a soma dos primeiros\(n\) termos de uma progressão aritmética é
\[S_n=\dfrac{n(a_1+a_n)}{2}\]
- Identifique\(a_1\)\(a_n\) e.
- Determinar\(n\).
- Substitua valores por\(a_1\)\(a_n\), e\(n\) na fórmula\(S_n=\dfrac{n(a_1+a_n)}{2}\).
- Simplifique para encontrar\(S_n\).
Encontre a soma de cada série aritmética.
- \(5 + 8 + 11 + 14 + 17 + 20 + 23 + 26 + 29 + 32\)
- \(20 + 15 + 10 +…+ −50\)
- \(\sum_{k=1}^{12}3k−8\)
Solução
- Recebemos\(a_1=5\)\(a_n=32\) e.
Conte o número de termos na sequência a ser encontrada\(n=10\).
Substitua valores por\(a_1\)\(a_n\), e\(n\) na fórmula e simplifique.
\[\begin{align*} S_n&=\dfrac{n(a_1+a_n)}{2}\\ S_{10}&=\dfrac{10(5+32)}{2}\\ &=185 \end{align*}\]
- Recebemos\(a_1=20\)\(a_n=−50\) e.
Use a fórmula para o termo geral de uma sequência aritmética para encontrar\(n\).
\[\begin{align*} a_n&=a_1+(n-1)d\\ -50&=20+(n-1)(-5)\\ -70&=(n-1)(-5)\\ 14&=n-1\\ 15&=n \end{align*}\]
Substitua valores por\(a_1\)\(a_n\),,\(n\) na fórmula e simplifique.
\[\begin{align*} S_n&=\dfrac{n(a_1+a_n)}{2}\\ S_{15}&=\dfrac{15(20-50)}{2}\\ &=-225 \end{align*}\]
- Para encontrar\(a_1\),\(k=1\) substitua pela fórmula explícita fornecida.
\[\begin{align*} a_k&=3k-8\\ a_1&=3(1)-8\\ &=-5 \end{align*}\]
Nós recebemos isso\(n=12\). Para encontrar\(a_12\),\(k=12\) substitua pela fórmula explícita fornecida.
\[\begin{align*} a_k&=3k-8\\ a_{12}&=3(12)-8\\ &=28 \end{align*}\]
Substitua valores por\(a_1\)\(a_n\), e\(n\) na fórmula e simplifique.
\[\begin{align*} S_n&=\dfrac{n(a_1+a_n)}{2}\\ S_{12}&=\dfrac{12(-5+28)}{2}\\ &=138 \end{align*}\]
Use a fórmula para encontrar a soma de cada série aritmética.
\(1.4 + 1.6 + 1.8 + 2.0 + 2.2 + 2.4 + 2.6 + 2.8 + 3.0 + 3.2 + 3.4\)
- Responda
-
\(26.4\)
\(13 + 21 + 29 + …+ 69\)
- Responda
-
\(328\)
\(\sum_{k=1}{10}5−6k\)
- Responda
-
\(−280\)
No domingo, após uma pequena cirurgia, uma mulher consegue andar 800 metros. Todos os domingos, ela caminha mais 400 metros. Depois de\(8\) semanas, qual será o número total de milhas que ela percorreu?
Solução
Esse problema pode ser modelado por uma série aritmética com\(a_1=\dfrac{1}{2}\)\(d=\dfrac{1}{4}\) e. Estamos procurando o número total de milhas percorridas após\(8\) semanas, então sabemos disso\(n=8\) e estamos procurando\(S_8\). Para descobrir\(a_8\), podemos usar a fórmula explícita para uma sequência aritmética.
\[\begin{align*} a_n&=a_1+d(n-1)\\ a_8&=\dfrac{1}{2}+\dfrac{1}{4}(8-1)\\ &=\dfrac{9}{4} \end{align*}\]
Agora podemos usar a fórmula para séries aritméticas.
\[\begin{align*} S_n&=\dfrac{n(a_1+a_n)}{2}\\ S_8&=\dfrac{8\left(\dfrac{1}{2}+\dfrac{9}{4}\right)}{2}\\ &=11 \end{align*}\]
Ela terá andado um total de\(11\) quilômetros.
Um homem ganha\($100\) na primeira semana de junho. A cada semana, ele ganha\($12.50\) mais do que na semana anterior. Depois de\(12\) semanas, quanto ele ganhou?
- Responda
-
\($2,025\)
Usando a fórmula para séries geométricas
Assim como a soma dos termos de uma sequência aritmética é chamada de série aritmética, a soma dos termos em uma sequência geométrica é chamada de série geométrica. Lembre-se de que uma sequência geométrica é uma sequência na qual a proporção de quaisquer dois termos consecutivos é a razão comum,\(r\). Podemos escrever a soma dos primeiros\(n\) termos de uma série geométrica como
\(S_n=a_1+ra_1+r^2a_1+...+r^{n–1}a_1\).
Assim como com séries aritméticas, podemos fazer alguma manipulação algébrica para derivar uma fórmula para a soma dos primeiros\(n\) termos de uma série geométrica. Começaremos multiplicando os dois lados da equação por\(r\).
\(rS_n=ra_1+r^2a_1+r^3a_1+...+r^na_1\)
Em seguida, subtraímos essa equação da equação original.
\[\begin{align*} S_n&=a_1+ra_1+r^2a_1+...+r^{n-1}a_1\\ \underline{-rS_n}&=\underline{-(ra_1+r^2a_1+r^3a_1+...+r^na_1)}\\ (1-r)S_n&=a_1-r^na_1 \end{align*}\]
Observe que quando subtraímos, todos, exceto o primeiro termo da equação superior e o último termo da equação inferior, são cancelados. Para obter uma fórmula para\(S_n\), divida os dois lados por\((1−r)\).
\(S_n=\dfrac{a_1(1−r^n)}{1−r}\)\(r≠1\)
Uma série geométrica é a soma dos termos em uma sequência geométrica. A fórmula para a soma dos primeiros\(n\) termos de uma sequência geométrica é representada como
\(S_n=\dfrac{a_1(1−r^n)}{1−r}\)\(r≠1\)
- Identifique\(a_1\)\(r\),\(n\) e.
- Substitua valores por\(a_1\)\(r\), e\(n\) na fórmula\(S_n=\dfrac{a_1(1−r^n)}{1−r}\).
- Simplifique para encontrar\(S_n\).
Use a fórmula para encontrar a soma parcial indicada de cada série geométrica.
- \(S_{11}\)para a série\(8 + -4 + 2 + …\)
- \(\sum_{ 6}^{k=1}3⋅2k\)
Solução
- \(a_1=8\), e isso nos é dado\(n=11\).
Podemos encontrar\(r\) dividindo o segundo termo da série pelo primeiro.
\(r=\dfrac{−4}{8}=−\dfrac{1}{2}\)
Substitua valores por\(a_1\)\(r\), e\(n\) na fórmula e simplifique.
\[\begin{align*} S_n&=\dfrac{a_1(1-r^n)}{1-r}\\ S_{11}&=\dfrac{8\left(1-{\left(-\dfrac{1}{2}\right)}^{11}\right)}{1-\left(-\dfrac{1}{2}\right)}\\ &\approx 5.336 \end{align*}\]
- Encontre\(a_1\)\(k=1\) substituindo a fórmula explícita fornecida.
\(a_1=3⋅2^1=6\)
Podemos ver pela fórmula explícita dada que\(r=2\). O limite superior da soma é\(6\), então\(n=6\).
Substitua valores por\(a_1\)\(r\), e\(n\) na fórmula e simplifique.
\[\begin{align*} S_n&=\dfrac{a_1(1-r^n)}{1-r}\\ S_6&=\dfrac{6(1-2^6)}{1-2}\\ &=378 \end{align*}\]
Use a fórmula para encontrar a soma parcial indicada de cada série geométrica.
\(S_{20}\)para a série\(1,000 + 500 + 250 + …\)
- Responda
-
\(≈2,000.00\)
\(\sum_{k=1}^{8}3^k\)
- Responda
-
\(9,840\)
Em um novo emprego, o salário inicial de um funcionário é\($26,750\). Ele recebe um aumento\(1.6\%\) anual. Encontre seus ganhos totais no final dos\(5\) anos.
Solução
O problema pode ser representado por uma série geométrica com\(a_1=26,750\)\(n=5\);;\(r=1.016\) e. Substitua valores por\(a_1\)\(r\), e\(n\) na fórmula e simplifique para encontrar o valor total ganho no final dos\(5\) anos.
\[\begin{align*} S_n&=\dfrac{a_1(1-r^n)}{1-r}\\ S_5&=\dfrac{26,750(1-{1.016}^5)}{1-1.016}\\ &\approx 138,099.03 \end{align*}\]
Ele terá ganho um total de\($138,099.03\) até o final dos\(5\) anos.
Em um novo emprego, o salário inicial de um funcionário é\($32,100\). Ela recebe um aumento\(2\%\) anual. Quanto ela terá ganho até o final dos\(8\) anos?
- Responda
-
\($275,513.31\)
Usando a fórmula para a soma de uma série geométrica infinita
Até agora, analisamos apenas séries finitas. Às vezes, no entanto, estamos interessados na soma dos termos de uma sequência infinita em vez da soma apenas dos primeiros\(n\) termos. Uma série infinita é a soma dos termos de uma sequência infinita. Um exemplo de uma série infinita é\(2+4+6+8+...\)
Essa série também pode ser escrita em notação de soma como\(\sum_{k=1}^{\infty}2k\), onde o limite superior da soma é infinito. Como os termos não tendem a zero, a soma da série aumenta sem limite à medida que adicionamos mais termos. Portanto, a soma dessa série infinita não está definida. Quando a soma não é um número real, dizemos que a série diverge.
Determinando se a soma de uma série geométrica infinita está definida
Se os termos de uma série geométrica infinita se aproximarem\(0\), a soma de uma série geométrica infinita pode ser definida. Os termos desta série abordam\(0\):
\(1+0.2+0.04+0.008+0.0016+...\)
A proporção comum\(r = 0.2\). Como\(n\) fica muito grande, os valores de\(r^n\) ficam muito pequenos e se aproximam\(0\). Cada termo sucessivo afeta a soma menor do que o termo anterior. À medida que cada termo sucessivo se aproxima\(0\), a soma dos termos se aproxima de um valor finito. Os termos de qualquer série geométrica infinita com\(−1<r<1\) abordagem\(0\); a soma de uma série geométrica é definida quando\(−1<r<1\).
A soma de uma série infinita é definida se a série for geométrica\(−1<r<1\) e.
- Encontre a proporção entre o segundo termo e o primeiro termo.
- Encontre a proporção do terceiro termo para o segundo termo.
- Continue esse processo para garantir que a proporção de um termo em relação ao termo anterior seja constante por toda parte. Nesse caso, a série é geométrica.
- Se uma proporção comum\(r\),, foi encontrada na etapa 3, verifique se\(−1<r<1\). Se sim, a soma é definida. Caso contrário, a soma não está definida.
Determine se a soma de cada série infinita está definida.
- \(12 + 8 + 4 + …\)
- \(\dfrac{3}{4}+\dfrac{1}{2}+\dfrac{1}{3}+...\)
- \(\sum_{k=1}^{\infty}27⋅{(\dfrac{1}{3})}^k\)
- \(\sum_{k=1}^{\infty}5k\)
Solução
- A proporção do segundo termo para o primeiro é\(\dfrac{2}{3}\), que não é a mesma que a razão do terceiro termo para o segundo,\(\dfrac{1}{2}\) .A série não é geométrica.
- A proporção do segundo termo para o primeiro é a mesma do terceiro termo para o segundo. A série é geométrica com uma proporção comum de\(\dfrac{2}{3}\). A soma das séries infinitas é definida.
- A fórmula dada é exponencial com uma base de\(\dfrac{1}{3}\); a série é geométrica com uma proporção comum de\(\dfrac{1}{3}\). A soma das séries infinitas é definida.
- A fórmula dada não é exponencial; a série não é geométrica porque os termos estão aumentando e, portanto, não podem produzir uma soma finita.
Determine se a soma das séries infinitas está definida.
\(\dfrac{1}{3}+\dfrac{1}{2}+\dfrac{3}{4}+\dfrac{9}{8}+...\)
- Responda
-
A soma está definida. É geométrico.
\(24+(−12)+6+(−3)+...\)
- Responda
-
A soma das séries infinitas é definida.
\(\sum_{k=1}^{\infty}15⋅{(–0.3)}^k\)
- Responda
-
A soma das séries infinitas é definida.
Encontrando somas de séries infinitas
Quando existe a soma de uma série geométrica infinita, podemos calcular a soma. A fórmula para a soma de uma série infinita está relacionada à fórmula para a soma dos primeiros\(n\) termos de uma série geométrica.
\[S_n=\dfrac{a_1(1−r^n)}{1−r}\]
Examinaremos uma série infinita com\(r=\dfrac{1}{2}\). O que acontece com\(r^n\) os\(n\) aumentos?
\[\begin{align*} \left(\dfrac{1}{2}\right)^2&=\dfrac{1}{4}\\ \left(\dfrac{1}{2}\right)^3&=\dfrac{1}{8}\\ \left(\dfrac{1}{2}\right)^4&=\dfrac{1}{16} \end{align*}\]
O valor de\(r^n\) diminui rapidamente. O que acontece com valores maiores de\(n\)?
\[\begin{align*} {\left(\dfrac{1}{2}\right)}^{10} &= \dfrac{1}{1,024} \\ {\left(\dfrac{1}{2}\right)}^{20} &= \dfrac{1}{1,048,576} \\ {\left(\dfrac{1}{2}\right)}^{30} &= \dfrac{1}{1,073,741,824} \end{align*}\]
Como\(n\) fica muito grande,\(r^n\) fica muito pequeno. Dizemos que, à medida que\(n\) aumenta sem limite,\(r^n\) se aproxima de 0. Conforme\(r^n\) se aproxima\(0\),\(1\),\(−r^n\) se aproxima\(1\). Quando isso acontece, o numerador se aproxima\(a_1\). Isso nos dá uma fórmula para a soma de uma série geométrica infinita.
A fórmula para a soma de uma série geométrica infinita com\(−1<r<1\) é
\[S=\dfrac{a_1}{1−r}\]
- Identifique\(a_1\)\(r\) e.
- Confirme isso\(–1<r<1\).
- Substitua valores por\(a_1\) e\(r\) na fórmula,\(S=\dfrac{a_1}{1−r}\).
- Simplifique para encontrar\(S\).
Encontre a soma, se existir, do seguinte:
- \(10+9+8+7+…\)
- \(248.6+99.44+39.776 + …\)
- \(\sum_{k=1}^{\infty}4,374⋅{(–\dfrac{1}{3})}^{k–1}\)
- \(\sum_{k=1}^{\infty}\dfrac{1}{9}⋅{(\dfrac{4}{3})}^k\)
Solução
- Não há uma proporção constante; a série não é geométrica.
- Há uma proporção constante; a série é geométrica. \(a_1=248.6\)e\(r=\dfrac{99.44}{248.6}=0.4\), portanto, a soma existe. Substitua\(a_1=248.6\) e\(r=0.4\) na fórmula e simplifique para encontrar a soma:
\[ \begin{align*} S&=\dfrac{a_1}{1−r} \\[4pt] &=\dfrac{248.6}{1−0.4} \\[4pt] &=414.\overline{3} \end{align*}\]
- A fórmula é exponencial, então a série é geométrica com\(r=–\dfrac{1}{3}\). Encontre\(a_1\)\(k=1\) substituindo a fórmula explícita fornecida:
\(a_1=4,374⋅{(–\dfrac{1}{3})}^{1–1}=4,374\)
Substitua\(a_1=4,374\) e\(r=−\dfrac{1}{3}\) na fórmula e simplifique para encontrar a soma:
\[ \begin{align*} S&=\dfrac{a_1}{1−r} \\[4pt] &= \dfrac{4,374}{1−\left(−\dfrac{1}{3}\right)} \\[4pt] &= 3,280.5 \end{align*}\]
- A fórmula é exponencial, então a série é geométrica, mas\(r>1\). A soma não existe.
Encontre uma fração equivalente para o decimal repetido\(0.\overline{3}\)
Solução
Percebemos o decimal repetido\(0.\overline{3}=0.333...\) para que possamos reescrever o decimal repetido como uma soma de termos.
\(0.\overline{3}=0.3+0.03+0.003+...\)
Procurando um padrão, reescrevemos a soma, percebendo que vemos o primeiro termo multiplicado para\(0.1\) no segundo termo e o segundo termo multiplicado para\(0.1\) no terceiro termo.

Observe o padrão; multiplicamos cada termo consecutivo por uma proporção comum de\(0.1\) começar com o primeiro termo de\(0.3\). Então, substituindo em nossa fórmula por uma soma geométrica infinita, temos
\(S_n=\dfrac{a_1}{1−r}=\dfrac{0.3}{1−0.1}=\dfrac{0.3}{0.9}=\dfrac{1}{3}\).
Encontre a soma, se ela existir.
\(2+23+29+...\)
- Responda
-
\(3\)
\(\sum_{k=1}^{\infty}0.76k+1\)
- Responda
-
A série não é geométrica.
\(\sum_{k=1}^{\infty}{\left(−\dfrac{3}{8}\right)}^k\)
- Responda
-
\(−\dfrac{3}{11}\)
Resolvendo problemas de anuidade
No início da seção, analisamos um problema no qual um casal investiu uma quantia fixa de dinheiro a cada mês em um fundo universitário por seis anos. Uma anuidade é um investimento no qual o comprador faz uma sequência de pagamentos periódicos e iguais. Para encontrar o valor de uma anuidade, precisamos encontrar a soma de todos os pagamentos e os juros auferidos. No exemplo, o casal investe\($50\) todo mês. Esse é o valor do depósito inicial. A conta pagava juros\(6\%\) anuais, compostos mensalmente. Para encontrar a taxa de juros por período de pagamento, precisamos dividir a taxa\(6\%\) anual de juros percentual (APR) por\(12\). Portanto, a taxa de juros mensal é\(0.5\%\). Podemos multiplicar o valor na conta a cada mês\(100.5\%\) para encontrar o valor da conta após a adição de juros.
Podemos encontrar o valor da anuidade logo após o último depósito usando uma série geométrica com\(a_1=50\)\(r=100.5%=1.005\) e. Após o primeiro depósito, o valor da anuidade será\($50\). Vamos ver se podemos determinar o valor do fundo da faculdade e os juros auferidos.
Podemos encontrar o valor da anuidade após nn depósitos usando a fórmula para a soma dos primeiros nn termos de uma série geométrica. Em\(6\) anos, há\(72\) meses, então\(n=72\). Podemos substituir\(a_1=50\)\(r=1.005\), e\(n=72\) na fórmula e simplificar para encontrar o valor da anuidade após 6 anos.
\(S_{72}=\dfrac{50(1−{1.005}^{72})}{1−1.005}≈4,320.44\)
Após o último depósito, o casal terá um total de\($4,320.44\) na conta. Aviso, o casal fez\(72\) pagamentos de\($50\) cada um, totalizando\(72(50) = $3,600\). Isso significa que, por causa da anuidade, o casal ganhou\($720.44\) juros no fundo da faculdade.
- Determine\(a_1\) o valor do depósito inicial.
- Determine\(n\) o número de depósitos.
- Determinar\(r\).
- Divida a taxa de juros anual pelo número de vezes por ano em que os juros são compostos.
- Adicione 1 a esse valor para encontrar\(r\).
- Substitua valores por\(a_1\)\(r\), e\(n\) na fórmula pela soma dos primeiros nn termos de uma série geométrica,\(S_n=\dfrac{a_1(1–r^n)}{1–r}\).
- Simplifique para encontrar\(S_n\) o valor da anuidade após\(n\) os depósitos.
Um depósito de\($100\) é colocado em um fundo universitário no início de cada mês durante\(10\) anos. O fundo ganha juros\(9\%\) anuais, compostos mensalmente e pagos no final do mês. Quanto está na conta logo após o último depósito?
Solução
O valor do depósito inicial é\($100\), portanto\(a_1=100\). Um total de depósitos\(120\) mensais são feitos ao\(10\) longo dos anos, então\(n=120\). Para encontrar\(r\), divida a taxa de juros anual por\(12\) para encontrar a taxa de juros mensal e adicione\(1\) para representar o novo depósito mensal.
\(r=1+\dfrac{0.09}{12}=1.0075\)
Substitua\(a_1=100\)\(r=1.0075\),, e\(n=120\) na fórmula pela soma dos primeiros\(n\) termos de uma série geométrica e simplifique para encontrar o valor da anuidade.
\(S_{120}=\dfrac{100(1−{1.0075}^{120})}{1−1.0075}≈19,351.43\)
Portanto, a conta tem $19.351,43 após o último depósito ser feito.
No início de cada mês,\($200\) é depositado em um fundo de aposentadoria. O fundo ganha juros\(6\%\) anuais, compostos mensalmente e pagos na conta no final do mês. Quanto há na conta se os depósitos forem feitos por\(10\) anos?
- Responda
-
\($92,408.18\)
Acesse esses recursos on-line para obter instruções e práticas adicionais com séries.
Equações-chave
| soma dos primeiros\(n\) termos de uma série aritmética | \(S_n=\dfrac{n(a_1+a_n)}{2}\) |
| soma dos primeiros\(n\) termos de uma série geométrica | \(S_n=\dfrac{a_1(1−r^n)}{1−r}\)‣\(r≠1\) |
| soma de uma série geométrica infinita com\(–1<r< 1\) | \(S_n=\dfrac{a_1}{1−r}\)‣\(r≠1\) |
Conceitos-chave
- A soma dos termos em uma sequência é chamada de série.
- Uma notação comum para séries é chamada de notação de soma, que usa a letra grega sigma para representar a soma. Veja o exemplo\(\PageIndex{1}\).
- A soma dos termos em uma sequência aritmética é chamada de série aritmética.
- A soma dos primeiros\(n\) termos de uma série aritmética pode ser encontrada usando uma fórmula. Veja o exemplo\(\PageIndex{2}\) e o exemplo\(\PageIndex{3}\).
- A soma dos termos em uma sequência geométrica é chamada de série geométrica.
- A soma dos primeiros\(n\) termos de uma série geométrica pode ser encontrada usando uma fórmula. Veja o exemplo\(\PageIndex{4}\) e o exemplo\(\PageIndex{5}\).
- A soma de uma série infinita existe se a série for geométrica com\(–1<r<1\).
- Se a soma de uma série infinita existir, ela pode ser encontrada usando uma fórmula. Veja exemplo\(\PageIndex{6}\)\(\PageIndex{7}\), exemplo e exemplo\(\PageIndex{8}\).
- Uma anuidade é uma conta na qual o investidor faz uma série de pagamentos regularmente programados. O valor de uma anuidade pode ser encontrado usando séries geométricas. Veja o exemplo\(\PageIndex{9}\).


