Skip to main content
Global

18.16: Ondas

  1. Last updated
  2. Save as PDF
  • Page ID
    184867

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    $ Verifique sua compreensão

    16.1. O comprimento de onda das ondas depende da frequência e da velocidade da onda. A frequência da onda sonora é igual à frequência da onda na corda. Os comprimentos de onda das ondas sonoras e das ondas na corda são iguais somente se as velocidades das ondas forem iguais, o que nem sempre é o caso. Se a velocidade da onda sonora for diferente da velocidade da onda na corda, os comprimentos de onda serão diferentes. Essa velocidade das ondas sonoras será discutida em Som.

    16.2. Em uma onda transversal, a onda pode se mover a uma velocidade de propagação constante pelo meio, mas o meio oscila perpendicularmente ao movimento da onda. Se a onda se mover na direção x positiva, o meio oscila para cima e para baixo na direção y. A velocidade do meio, portanto, não é constante, mas a velocidade e a aceleração do meio são semelhantes às do movimento harmônico simples de uma massa em uma mola.

    16.3. Sim, uma função de cosseno é igual a uma função senoidal com uma mudança de fase, e qualquer uma das funções pode ser usada em uma função de onda. Qual função é mais conveniente de usar depende das condições iniciais. Na Figura 16.11, a onda tem uma altura inicial de y (0,00, 0,00) = 0 e, em seguida, a altura da onda aumenta até a altura máxima na crista. Se a altura inicial no momento inicial fosse igual à amplitude da onda y (0,00, 0,00) = +A, então seria mais conveniente modelar a onda com uma função de cosseno.

    16,4. Essa onda, com amplitude A = 0,5 m, comprimento de onda\(\lambda\) = 10,00 m, período T = 0,50 s, é uma solução para a equação da onda com uma velocidade de onda v = 20,00 m/s.

    16,5. Como a velocidade de uma onda em uma corda provocadora é proporcional à raiz quadrada da tensão dividida pela densidade linear, a velocidade da onda aumentaria em\(\sqrt{2}\).

    16,6. À primeira vista, a potência média temporal de uma onda senoidal em uma corda pode parecer proporcional à densidade linear da corda porque P =\(\frac{1}{2} \mu\) A 2\(\omega^{2}\) v; no entanto, a velocidade da onda depende da densidade linear. Substituir a velocidade da onda por\(\sqrt{\frac{F_{T}}{\mu}}\) mostra que a potência é proporcional à raiz quadrada da tensão e proporcional à raiz quadrada da densidade de massa linear:\[P = \frac{1}{2} \mu A^{2} \omega^{2} v = \frac{1}{2} \mu A^{2} \omega^{2} \sqrt{\frac{F_{T}}{\mu}} = \frac{1}{2} A^{2} \omega^{2} \sqrt{\mu F_{T}} \ldotp\]

    16,7. Sim, as equações funcionariam igualmente bem para condições de contorno simétricas de um meio livre para oscilar em cada extremidade onde havia um antinodo em cada extremidade. Os modos normais dos três primeiros modos são mostrados abaixo. A linha pontilhada mostra a posição de equilíbrio do meio.

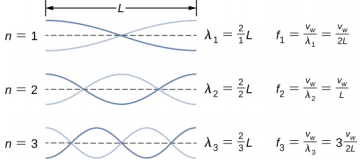
    Três figuras de uma corda de comprimento L são mostradas. Cada um tem duas ondas. O primeiro tem 1 nó. É rotulado lambda 1 = 2 por 1 vezes L, f1 = vw por lambda 1 = vw por 2L. A segunda figura tem 2 nós. É rotulado lambda 2 = 2 por 2 vezes L, f2 = vw por lambda 2 = vw por L. A terceira figura tem três nós. É rotulado lambda 3 = 2 por 3 vezes L, f3 = vw por lambda 3 igual a 3 vezes vw por 2L.

    Observe que o primeiro modo tem dois quartos, ou metade, de um comprimento de onda. O segundo modo tem um quarto do comprimento de onda, seguido pela metade do comprimento de onda, seguido por um quarto do comprimento de onda ou um comprimento de onda completo. O terceiro modo tem um comprimento de onda e meio. Esses são o mesmo resultado da string com um nó em cada extremidade. As equações para condições de contorno simétricas funcionam igualmente bem para condições de contorno fixo e condições de contorno livre. Esses resultados serão revisitados no próximo capítulo ao discutir a onda sonora em um tubo aberto.

    Perguntas conceituais

    1. Uma onda em uma corda de violão é um exemplo de onda transversal. A perturbação da corda se move perpendicularmente à propagação da onda. O som produzido pela corda é uma onda longitudinal em que a perturbação do ar se move paralelamente à propagação da onda.

    3. A velocidade de propagação é a velocidade da onda que se propaga pelo meio. Se a velocidade da onda for constante, a velocidade pode ser encontrada por v =\(\frac{\lambda}{T}\) =\(\lambda\) f. A frequência é o número de ondas que passam por um ponto por unidade de tempo. O comprimento de onda é diretamente proporcional à velocidade da onda e inversamente proporcional à frequência.

    5. Não, a distância em que você move a mão para cima e para baixo determinará a amplitude da onda. O comprimento de onda dependerá da frequência com que você move a mão para cima e para baixo e da velocidade da onda na mola.

    7. A luz do Sol e das estrelas chega à Terra através do espaço vazio onde não há meio presente.

    9. O comprimento de onda é igual à velocidade da onda vezes a frequência e o número da onda é igual a k =\(\frac{2 \pi}{\lambda}\), então sim, o número da onda dependerá da frequência e também da velocidade da onda que se propaga pela mola.

    11. O meio se move em movimento harmônico simples à medida que a onda se propaga pelo meio, mudando continuamente a velocidade, portanto, ele acelera. A aceleração do meio se deve à força restauradora do meio, que atua na direção oposta ao deslocamento.

    13. A velocidade da onda é proporcional à raiz quadrada da tensão, então a velocidade é dobrada.

    15. Como a velocidade de uma onda em uma corda é inversamente proporcional à raiz quadrada da densidade de massa linear, a velocidade seria maior na baixa densidade de massa linear da corda.

    17. A tensão no fio é devida ao peso do cabo de alimentação elétrica.

    19. A potência média do tempo é P\(\frac{E_{\lambda}}{T}\) = A 2\(\frac{1}{2} \mu\)\(\omega^{2} \frac{\lambda}{T} = \frac{1}{2} \mu\) A 2\(\omega^{2}\) v. Se a frequência ou a amplitude forem reduzidas pela metade, a potência diminui em um fator de 4.

    21. À medida que uma parte da corda se move verticalmente, ela exerce uma força na parte vizinha da corda, trabalhando na parte e transferindo a energia.

    23. A intensidade de uma onda esférica é I =\(\frac{P}{4 \pi r^{2}}\), se nenhuma energia for dissipada, a intensidade diminuirá em um fator de nove a três metros.

    25. Na interface, o pulso incidente produz um pulso refletido e um pulso transmitido. O pulso refletido estaria fora de fase em relação ao pulso incidente e se moveria na mesma velocidade de propagação do pulso incidente, mas se moveria na direção oposta. O pulso transmitido viajaria na mesma direção do pulso incidente, mas na metade da velocidade. O pulso transmitido estaria em sintonia com o pulso incidente. Tanto o pulso refletido quanto o pulso transmitido teriam amplitudes menores que a amplitude do pulso incidente.

    27.

    A figura mostra o gráfico de uma onda. Seu valor y é 0 em x=0. Em x=3, o valor y sobe para 4 e permanece constante até x=5. Aqui, ele sobe para 5 e permanece constante até x=7. Aqui, ele cai para 2 e permanece constante até x=8. Aqui, ele cai para -3 e permanece constante até x=9. Aqui, ele sobe para 0 e permanece constante.

    29. Pode ser tão fácil quanto alterar o comprimento e/ou a densidade em uma pequena quantidade para que as peças não ressoem na frequência do motor.

    31. A energia é fornecida ao vidro pelo trabalho realizado pela força do dedo no vidro. Quando fornecidas na frequência certa, formam-se ondas estacionárias. O vidro ressoa e as vibrações produzem som.

    33. Para a equação y (x, t) = 4,00 cm sin (3 m −1 x) cos (4 s −1 t), existe um nó porque quando x = 0,00 m, sin (3 m −1 (0,00 m)) = 0,00, então y (0,00 m, t) = 0,00 m para sempre. Para a equação y (x, t) = 4,00 cm sin (3 m −1 x +\(\frac{\pi}{2}\)) cos (4 s −1 t), existe um antinodo porque quando x = 0,00 m, sin (3 m −1 (0,00 m) +\(\frac{\pi}{2}\)) = + 1,00, então y (0,00 m, t) oscila entre +A e −A à medida que o termo cosseno oscila entre +1 e -1.

    Problemas

    35. 2d = vt\(\Rightarrow\) d = 11,25 m

    37. v = f\(\lambda\), de modo que f = 0,125 Hz, então N = 7,50 vezes

    39. v = f\(\lambda \Rightarrow \lambda\) = 0,400 m

    41. v = f\(\lambda \Rightarrow\) f = 2,50 x 10 9 Hz

    43. a. As ondas P superam as ondas S em uma velocidade de v = 3,20 km/s; portanto,\(\Delta\) d = 0,320 km.

    b. Como a incerteza na distância é inferior a um quilômetro, nossa resposta à parte (a) não parece limitar a detecção de detonações de bombas nucleares. No entanto, se as velocidades forem incertas, a incerteza na distância aumentaria e poderia dificultar a identificação da origem das ondas sísmicas.

    45. v = 1900 m/s,\(\Delta\) t = 1,05\(\mu\) s

    47. y (x, t) = −0,037 cm

    49. O pulso se moverá\(\Delta\) x = 6,00 m.

    A figura mostra duas ondas de pulso. Ambos têm valores de y variando de 0 a 1. A primeira onda, mostrada como uma linha pontilhada, está marcada com t=0 segundos. A crista da onda está em x=0. A segunda onda, mostrada como uma linha sólida, é marcada com t= 3 segundos. A crista da onda está em x=6.

    51. a. A = 0,25 m

    b. k = 0,30 m −1

    c.\(\omega\) = 0,90 s −1

    d. v = 3,0 m/s

    e.\(\phi\) =\(\frac{\pi}{3}\) ler

    f.\(\lambda\) = 20,93 m

    g. T = 6,98 s

    53. A = 0,30 m,\(\lambda\) = 4,50 m, v = 18,00 m/s, f = 4,00 Hz, T = 0,25 s

    55. y (x, t) = 0,23 m sin (3,49 m −1 x − 0,63 s −1 t)

    57. Eles têm a mesma frequência angular, frequência e período. Eles estão viajando em direções opostas e y 2 (x, t) tem o dobro do comprimento de onda de y 1 (x, t) e está se movendo na metade da velocidade da onda.

    59. Cada partícula do meio se move a uma distância de 4A a cada período. O período pode ser encontrado dividindo a velocidade pelo comprimento de onda: t = 10,42 s

    61. a.\(\mu\) = 0,040 kg/m

    b. v = 15,75 m/s

    63. v = 180 m/s

    65. v = 547,723 m/s,\(\Delta\) t = 5,48 ms

    67. v s = 347,56 m/s

    69. v 1 t + v 2 t = 2,00 m, t = 1,69 ms

    71. v = 288,68 m/s,\(\lambda\) = 0,73 m

    73. a. A = 0,0125 cm

    b. F T = 0,96 N

    75. v = 74,54 m/s,\(P_{\lambda}\) = 91,85 W

    77. I = 20,0 W/m 2

    b. I =\(\frac{P}{A}\), A = 10,0 m2 A = 4\(\pi\) r 2, r = 0,892 m

    79. I = 650 W/m 2

    81. \[P \propto E \propto I \propto X^{2} \Rightarrow \frac{P_{2}}{P_{1}} = \left(\dfrac{X_{2}}{X_{1}}\right)^{2}\]

    P 2 = 2,50 kW

    83. \[I \propto X^{2} \Rightarrow \frac{I_{1}}{I_{2}} = \left(\dfrac{X_{1}}{X_{2}}\right)^{2}\]

    I 2 = 3,38 x 10 −5 W/m 2

    85. f = 100,00 Hz, A = 1,10 cm

    87. a. I 2 = 0,063I 1

    b. I 1 4\(\pi\) r 1 2 = I 2 4\(\pi\) r 2 2, r 2 = 3,16 m

    89. 2\(\pi\) r 1 A 1 2 = 2\(\pi\) r 2 A 2 2, A 1 =\(\left(\dfrac{r_{2}}{r_{1}}\right)^{1/2}\), A 1 = 0,17 m

    91. y (x, t) = 0,76 m

    93. A R = 2A cos\(\left(\dfrac{\phi}{2}\right)\),\(\phi\) = 1,17 rad

    95. y R = 1,90 cm

    97. \(\omega\)= 6,28 s −1, k = 3,00 m −1,\(\phi\) =\(\frac{\pi}{8}\) rad, A R = 2A cos\(\left(\dfrac{\phi}{2}\right)\), A = 0,37 m

    99. uma.

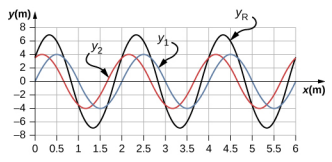
    A figura mostra uma onda azul chamada y1, uma onda vermelha chamada y2 e uma onda preta chamada yR no mesmo gráfico. As ondas vermelha e azul têm o mesmo comprimento de onda e amplitude, mas estão fora de fase. A onda preta tem o mesmo comprimento de onda das outras duas, mas é maior em amplitude.

    b.\(\lambda\) = 2,0 m, A = 4 m

    c.\(\lambda_{R}\) = 2,0 m, A R = 6,93 m

    101. y R (x, t) = 2A cos\(\left(\dfrac{\phi}{2}\right)\) cos\(\left(kx − \omega t + \dfrac{\phi}{2}\right)\); O resultado não é surpreendente porque cos (\(\theta\)) = sin (\(\theta + \frac{\pi}{2}\)).

    103. \[\begin{split} \lambda_{n} & = \frac{2.00}{n} L, \quad f_{n} = \frac{v}{\lambda_{n}} \\ \lambda_{1} & = 4.00\; m, \quad f_{1} = 12.5\; Hz \\ \lambda_{2} & = 2.00\; m, \quad f_{2} = 25.00\; Hz \\ \lambda_{3} & = 1.33\; m, \quad f_{3} = 37.59\; Hz \end{split}\]

    105. v = 158,11 m/s,\(\lambda\) = 4,44 m, f = 35,61 Hz,\(\lambda_{s}\) = 9,63 m

    107. y (x, t) = [0,60 cm sin (3 m −1 x)] cos (4 s −1 t)

    109. \[\begin{split} \lambda_{100} & = 0.06\; m \\ v & = 56.8\; m/s, \quad f_{n} = n f_{1}, \quad n = 1, 2, 3, 4, 5 \ldots \\ f_{100} & = 947\; Hz \end{split}\]

    111. T = 2\(\Delta\) t, v =\(\frac{\lambda}{T}\),\(\lambda\) = 2,12 m

    113. \(\lambda_{1}\)= 6,00 m,\(\lambda_{2}\) = 3,00 m,\(\lambda_{3}\) = 2,00 m,\(\lambda_{4}\) = 1,50 m; v = 258,20 m/s =\(\lambda\) f; f 1 = 43,03 Hz, f 2 = 86,07 Hz, f 3 = 129,10 Hz, f 4 = 172,13 Hz

    115. v = 134,16 ms,\(\lambda\) = 1,4 m, f = 95,83 Hz, T = 0,0104 s

    Problemas adicionais

    117. \(\lambda\)= 0,10 m

    119. a. f = 4,74 x 10 14 Hz

    b.\(\lambda\) = 422 mm

    121. \(\lambda\)= 16,00 m, f = 0,10 Hz, T = 10,00 s, v = 1,6 m/s

    123. \(\lambda\)= (v b + v) t b, v = 3,75 m/s,\(\lambda\) = 3,00 m

    125. \[\begin{split} \frac{\partial^{2} (y_{1} + y_{2})}{\partial t^{2}} & = -A \omega^{2} \sin (kx - \omega t) - A \omega^{2} \sin (kx - \omega t + \phi) \\ \frac{\partial^{2} (y_{1} + y_{2})}{\partial x^{2}} & = -Ak^{2} \sin (kx - \omega t) - Ak^{2} \sin (kx - \omega t + \phi) \\ \frac{\partial^{2} y(x,t)}{\partial x^{2}} & = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}} \\ -A \omega^{2} \sin (kx - \omega t) - A \omega^{2} \sin (kx - \omega t + \phi) & = \left(\dfrac{1}{v^{2}}\right) (-Ak^{2} \sin (kx - \omega t) - Ak^{2} \sin (kx - \omega t + \phi)) \\ v & = \frac{\omega}{k} \end{split}\]

    127. y (x, t) = 0,40 m sin (0,015 m −1 x + 1,5 s −1 t)

    129. v = 223,61 m/s, k = 1,57 m −1,\(\omega\) = 142,43 s −1

    131. P =\(\frac{1}{2}\) A 2 (2\(\pi\) f) 2\(\sqrt{\mu F_{T}}\),\(\mu\) = 2,00 x 10 −4 kg/m

    133. P =\(\frac{1}{2} \mu\) A 2\(\omega^{2} \frac{\lambda}{T}\),\(\mu\) = 0,0018 kg/m

    135. a. A R = 2A cos\(\left(\dfrac{\phi}{2}\right)\), cos\(\left(\dfrac{\phi}{2}\right)\) = 1,\(\phi\) = 0, 2\(\pi\), 4\(\pi\),...

    b. A R = 2A cos\(\left(\dfrac{\phi}{2}\right)\), cos\(\left(\dfrac{\phi}{2}\right)\) = 0,\(\phi\) = 0\(\pi\), 3\(\pi\), 5\ (\ pi),...

    137. y R (x, t) = 0,6 m sin (4 m −1) cos (3 s −1 t)

    139. uma.\[\begin{split} &F_{T} - 20.00\; kg(9.80\; m/s^{2}) \cos 45^{o} & = 0 \\ &m(9.80\; m/s^{2}) - F_{T} = 0 \\ &m = 14.14\; kg \end{split}\]

    b. F T = 138,57 N, v = 74,45 m/s

    141. F T = 2 N, v = 6,73 m/s

    143. a. f n =\(\frac{nv}{2L}\), v =\(\frac{2L f_{n + 1}}{n + 1}\)\(\frac{n + 1}{n} = \frac{2L f_{n + 1}}{2L f_{n}}\), 1 +\(\frac{1}{n}\) = 1,2, n = 5;\(\lambda_{n}\) =\(\frac{2}{n}\) L,\(\lambda_{5}\) = 1,6 m,\(\lambda_{6}\) = 1,33 m

    b. F T = 245,76 N

    Problemas de desafio

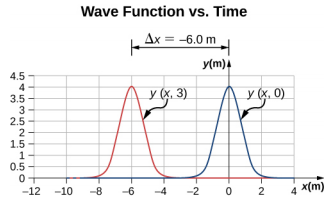
    145. a. Move-se na direção x negativa a uma velocidade de propagação de v = 2,00 m/s.

    b.\(\Delta\) x = −6,00 m

    c.

    A figura mostra um gráfico denominado função de onda versus tempo. Duas ondas de pulso idênticas são mostradas no gráfico. A onda vermelha, chamada y parênteses x, 3, atinge o pico em x = -6 m. A onda azul, rotulada com y parênteses x, 0, atinge o pico em x = 0 m. A distância entre os dois picos é rotulada como delta x = -6 m.

    147. \[\begin{split} \sin(kx - \omega t) & = \sin \left(kx + \dfrac{\phi}{2}\right) \cos \left(\omega t + \dfrac{\phi}{2}\right) - \cos \left(kx + \dfrac{\phi}{2}\right) \sin \left(\omega t + \dfrac{\phi}{2}\right) \\ \sin(kx - \omega t + \phi) & = \sin \left(kx + \dfrac{\phi}{2}\right) \cos \left(\omega t + \dfrac{\phi}{2}\right) + \cos \left(kx + \dfrac{\phi}{2}\right) \sin \left(\omega t + \dfrac{\phi}{2}\right) \\ \sin(kx - \omega t) + \sin(kx - \omega t + \phi) & = 2 \sin \left(kx + \dfrac{\phi}{2}\right) \cos \left(\omega t + \frac{\phi}{2}\right) \\ y_{R} & = 2A \sin \left(kx + \frac{\phi}{2}\right) \cos \left(\omega t + \dfrac{\phi}{2}\right) \end{split}\]

    149. sin\(\left(kx + \dfrac{\phi}{2}\right)\) = 0, kx +\(\frac{\phi}{2}\) = 0\(\pi\), 2\(\pi\), 1,26 m −1 x +\(\frac{\pi}{20}\) =\(\pi\), 2\(\pi\), 3\(\pi\); x = 2,37 m, 4,86 m, 7,35 m

    A figura mostra um gráfico com a onda y1 em azul, onda y2 em vermelho e onda y1 mais y2 em preto. Todas as três têm um comprimento de onda de 5 m. As ondas y1 e y2 têm a mesma amplitude e estão ligeiramente fora de fase uma com a outra. A amplitude da onda preta é quase o dobro da das outras duas.

    Contribuidores e atribuições

    Template:ContribOpenStaxUni