15.7: Oscilações forçadas

Objetivos de

• Defina oscilações forçadas
• Liste as equações de movimento associadas às oscilações forçadas
• Explique o conceito de ressonância e seu impacto na amplitude de um oscilador
• Listar as características de um sistema que oscila em ressonância

Sente-se em frente a um piano em algum momento e cante uma breve nota alta com os amortecedores fora das cordas (Figura\(\PageIndex{1}\)). Ele cantará a mesma nota para você — as cordas, com as mesmas frequências da sua voz, estão ressoando em resposta às forças das ondas sonoras que você enviou para elas. Esse é um bom exemplo do fato de que objetos — neste caso, cordas de piano — podem ser forçados a oscilar e oscilar mais facilmente em sua frequência natural. Nesta seção, exploramos brevemente a aplicação de uma força motriz periódica atuando em um oscilador harmônico simples. A força motriz coloca energia no sistema em uma determinada frequência, não necessariamente a mesma que a frequência natural do sistema. Lembre-se de que a frequência natural é a frequência na qual um sistema oscilaria se não houvesse força de acionamento nem de amortecimento.

Figura\(\PageIndex{1}\): - Você pode fazer com que as cordas de um piano vibrem simplesmente produzindo ondas sonoras de sua voz.

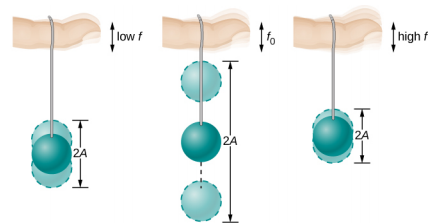
A maioria de nós já brincou com brinquedos envolvendo um objeto apoiado em um elástico, algo como a bola de remo suspensa de um dedo na Figura\(\PageIndex{2}\). Imagine que o dedo na figura é seu dedo. No início, você mantém o dedo firme e a bola salta para cima e para baixo com uma pequena quantidade de amortecimento. Se você mover o dedo para cima e para baixo lentamente, a bola segue em frente sem saltar muito sozinha. À medida que você aumenta a frequência com que você move o dedo para cima e para baixo, a bola responde oscilando com amplitude crescente. Quando você dirige a bola em sua frequência natural, as oscilações da bola aumentam em amplitude a cada oscilação enquanto você a dirige. O fenômeno de dirigir um sistema com uma frequência igual à sua frequência natural é chamado de ressonância. Diz-se que um sistema acionado em sua frequência natural ressoa. À medida que a frequência de condução se torna progressivamente maior do que a frequência ressonante ou natural, a amplitude das oscilações se torna menor até que as oscilações quase desapareçam, e seu dedo simplesmente se move para cima e para baixo com pouco efeito na bola.

Figura\(\PageIndex{2}\): A bola de remo em seu elástico se move em resposta ao dedo que a apoia. Se o dedo se mover com a frequência natural f0 da bola no elástico, então uma ressonância é alcançada e a amplitude das oscilações da bola aumenta dramaticamente. Em frequências de condução mais altas e mais baixas, a energia é transferida para a bola com menos eficiência e ela responde com oscilações de menor amplitude.

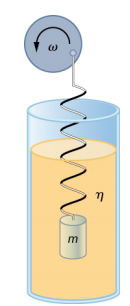
Considere um experimento simples. Conecte uma massa m a uma mola em um fluido viscoso, semelhante ao aparelho discutido no oscilador harmônico amortecido. Desta vez, em vez de fixar a extremidade livre da mola, conecte a extremidade livre a um disco acionado por um motor de velocidade variável. O motor gira com uma frequência de condução angular de ω. O disco giratório fornece energia ao sistema pelo trabalho realizado pela força motriz (F _d = F ₀ sin (\(\omega\)t)). O aparato experimental é mostrado na Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Movimento harmônico forçado e amortecido produzido ao acionar uma mola e uma massa com um disco acionado por um motor de velocidade variável.

Usando a segunda lei de Newton (\(\vec{F}_{net} = m \vec{a}\)), podemos analisar o movimento da massa. A equação resultante é semelhante à equação da força para o oscilador harmônico amortecido, com a adição da força motriz:

\[-kx -b \frac{dx}{dt} + F_{0} \sin (\omega t) = m \frac{d^{2} x}{dt^{2}} \ldotp \label{15.27}\]

Quando um oscilador é forçado com uma força motriz periódica, o movimento pode parecer caótico. Os movimentos do oscilador são conhecidos como transientes. Depois que os transientes desaparecem, o oscilador atinge um estado estacionário, onde o movimento é periódico. Depois de algum tempo, a solução de estado estacionário para essa equação diferencial é

\[x(t) = A \cos (\omega t + \phi) \ldotp \label{15.28}\]

Mais uma vez, resta como um exercício para provar que essa equação é uma solução. Tomar a primeira e a segunda derivada de x (t) e substituí-las na equação da força mostra que x (t) = Asin (\(\omega t + \phi\)) é uma solução, desde que a amplitude seja igual a

\[A = \frac{F_{0}}{\sqrt{m^{2} (\omega^{2} - \omega_{0}^{2})^{2} + b^{2} \omega^{2}}} \label{15.29}\]

onde\(\omega_{0} = \sqrt{\frac{k}{m}}\) está a frequência angular natural do sistema da massa e da mola. Lembre-se de que a frequência angular e, portanto, a frequência do motor podem ser ajustadas. Observando o denominador da equação para a amplitude, quando a frequência de condução é muito menor ou muito maior que a frequência natural, o quadrado da diferença das duas frequências angulares\((\omega^{2} − \omega_{0}^{2})^{2}\) é positivo e grande, tornando o denominador grande, e o resultado é uma pequena amplitude para as oscilações da massa. À medida que a frequência da força motriz se aproxima da frequência natural do sistema, o denominador se torna pequeno e a amplitude das oscilações se torna grande. A amplitude máxima ocorre quando a frequência da força motriz é igual à frequência natural do sistema (A _max =\(\frac{F_{0}}{b \omega}\)).

A figura\(\PageIndex{4}\) mostra um gráfico da amplitude de um oscilador harmônico amortecido em função da frequência da força periódica que o impulsiona. Cada uma das três curvas no gráfico representa uma quantidade diferente de amortecimento. Todas as três curvas atingem o pico no ponto em que a frequência da força motriz é igual à frequência natural do oscilador harmônico. O pico mais alto, ou maior resposta, é para a menor quantidade de amortecimento, porque menos energia é removida pela força de amortecimento. Observe que, como a amplitude aumenta à medida que o amortecimento diminui, levando-a ao limite onde não há amortecimento (b = 0), a amplitude se torna infinita.

Observe que uma força motriz de pequena amplitude pode produzir uma resposta de grande amplitude. Esse fenômeno é conhecido como ressonância. Um exemplo comum de ressonância é um pai empurrando uma criança pequena em um balanço. Quando a criança quer subir mais alto, os pais não recuam e depois, começando a correr, batem na criança, aplicando uma grande força em um curto intervalo. Em vez disso, o pai aplica pequenos empurrões na criança na frequência certa e a amplitude das oscilações da criança aumenta.

Figura\(\PageIndex{4}\): Amplitude de um oscilador harmônico em função da frequência da força motriz. As curvas representam o mesmo oscilador com a mesma frequência natural, mas com diferentes quantidades de amortecimento. A ressonância ocorre quando a frequência de condução é igual à frequência natural, e a maior resposta é para a menor quantidade de amortecimento. A resposta mais estreita também é para o menor amortecimento.

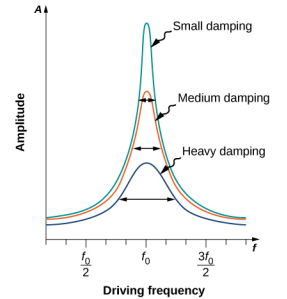
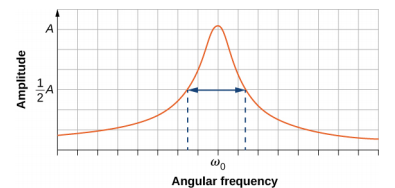
É interessante observar que as larguras das curvas de ressonância mostradas na Figura\(\PageIndex{4}\) dependem do amortecimento: quanto menor o amortecimento, mais estreita é a ressonância. A consequência é que, se você quiser que um oscilador acionado ressoe em uma frequência muito específica, precisará do mínimo de amortecimento possível. Por exemplo, um rádio tem um circuito usado para escolher uma estação de rádio específica. Nesse caso, o oscilador amortecido forçado consiste em um resistor, capacitor e indutor, que serão discutidos posteriormente neste curso. O circuito é “sintonizado” para escolher uma estação de rádio específica. Aqui é desejável que a curva de ressonância seja muito estreita, para escolher a frequência exata da estação de rádio escolhida. A estreiteza do gráfico e a capacidade de escolher uma determinada frequência são conhecidas como a qualidade do sistema. A qualidade é definida como a dispersão da frequência angular, ou equivalentemente, a dispersão na frequência, na metade da amplitude máxima, dividida pela frequência natural (Q =\(\frac{\Delta \omega}{\omega_{0}}\)), conforme mostrado na Figura\(\PageIndex{5}\). Para um pequeno amortecimento, a qualidade é aproximadamente igual a Q ≈\(\frac{2b}{m}\).

Figura\(\PageIndex{5}\): A qualidade de um sistema é definida como a dispersão nas frequências na metade da amplitude dividida pela frequência natural.

Essas características dos osciladores harmônicos acionados se aplicam a uma grande variedade de sistemas. Por exemplo, a ressonância magnética (MRI) é uma ferramenta de diagnóstico médico amplamente usada na qual núcleos atômicos (principalmente núcleos de hidrogênio ou prótons) são feitos para ressoar pelas ondas de rádio recebidas (na ordem de 100 MHz). Em todos esses casos, a eficiência da transferência de energia da força motriz para o oscilador é melhor na ressonância. A figura\(\PageIndex{6}\) mostra a London Millennium Footbridge, que permite que os pedestres cruzem o rio Tâmisa em Londres. Essa ponte foi apelidada de “Ponte Vacilante” quando os pedestres experimentaram movimentos oscilantes ao atravessá-la. A ponte ficou fechada por cerca de dois anos para se livrar desse movimento.

Figura\(\PageIndex{6}\): Inicialmente, quando as pessoas cruzaram a London Millennium Footbridge, elas experimentaram um movimento oscilante. As pessoas que continuaram cruzando reforçaram a amplitude da oscilação, aumentando assim a oscilação problemática. (crédito: Adrian Pingstone/Wikimedia Commons)

Exercício 15.6

Um famoso truque de mágica envolve um artista cantando uma nota em direção a um copo de cristal até que o copo se estilhaça. Explique por que o truque funciona em termos de ressonância e frequência natural.