15.3: Energia em movimento harmônico simples

Objetivos de

• Descreva a conservação de energia do sistema de uma massa e uma mola
• Explicar os conceitos de pontos de equilíbrio estáveis e instáveis

Para produzir uma deformação em um objeto, devemos trabalhar. Ou seja, se você puxar uma corda de guitarra ou comprimir o amortecedor de um carro, uma força deve ser exercida à distância. Se o único resultado for deformação e nenhum trabalho for transformado em energia térmica, sonora ou cinética, todo o trabalho é inicialmente armazenado no objeto deformado como alguma forma de energia potencial.

Considere o exemplo de um bloco preso a uma mola em uma mesa sem atrito, oscilando em SHM. A força da mola é uma força conservadora (que você estudou no capítulo sobre energia potencial e conservação de energia), e podemos definir uma energia potencial para ela. Essa energia potencial é a energia armazenada na primavera quando a mola é estendida ou comprimida. Nesse caso, o bloco oscila em uma dimensão com a força da mola atuando paralelamente ao movimento:

\[W = \int_{x_{i}}^{x_{f}} F_{x} dx \int_{x_{i}}^{x_{f}} -kxdx = \Big[ - \frac{1}{2} kx^{2} \Big]_{x_{i}}^{x_{f}} = - \Big[ \frac{1}{2} kx_{f}^{2} - \frac{1}{2} kx_{i}^{2} \Big] = - [U_{f} - U_{i}] = - \Delta U \ldotp\]

Ao considerar a energia armazenada em uma mola, a posição de equilíbrio, marcada como x _i = 0,00 m, é a posição na qual a energia armazenada na mola é igual a zero. Quando a mola é esticada ou comprimida a uma distância x, a energia potencial armazenada na mola é

\[U = \frac{1}{2} kx^{2} \ldotp\]

Energia e o oscilador harmônico simples

Para estudar a energia de um oscilador harmônico simples, precisamos considerar todas as formas de energia. Considere o exemplo de um bloco preso a uma mola, colocado em uma superfície sem atrito, oscilando em SHM. A energia potencial armazenada na deformação da mola é

\[U = \frac{1}{2} kx^{2} \ldotp\]

Em um oscilador harmônico simples, a energia oscila entre a energia cinética da massa K =\(\frac{1}{2}\) mv ² e a energia potencial U =\(\frac{1}{2}\) kx ² armazenada na mola. No SHM do sistema de massa e mola, não há forças dissipativas, então a energia total é a soma da energia potencial e da energia cinética. Nesta seção, consideramos a conservação da energia do sistema. Os conceitos examinados são válidos para todos os osciladores harmônicos simples, incluindo aqueles em que a força gravitacional desempenha um papel.

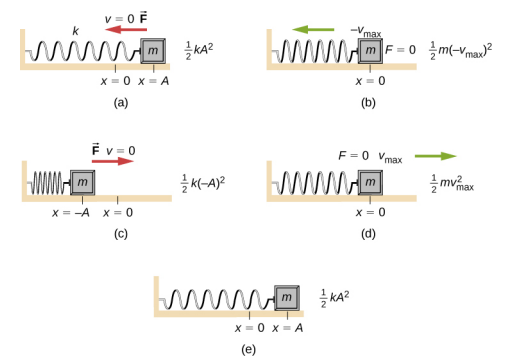
Considere a Figura\(\PageIndex{1}\), que mostra um bloco oscilante preso a uma mola. No caso de SHM sem amortecimento, a energia oscila para frente e para trás entre a cinética e o potencial, indo completamente de uma forma de energia para a outra à medida que o sistema oscila. Portanto, para o exemplo simples de um objeto em uma superfície sem atrito presa a uma mola, o movimento começa com toda a energia armazenada na mola como energia potencial elástica. Quando o objeto começa a se mover, a energia potencial elástica é convertida em energia cinética, tornando-se energia inteiramente cinética na posição de equilíbrio. A energia é então convertida novamente em energia potencial elástica pela mola à medida que é esticada ou comprimida. A velocidade se torna zero quando a energia cinética é completamente convertida e esse ciclo se repete. Compreender a conservação de energia nesses ciclos fornecerá uma visão extra aqui e em aplicações posteriores do SHM, como circuitos alternados.

Figura\(\PageIndex{1}\): A transformação de energia em SHM para um objeto preso a uma mola em uma superfície sem atrito. (a) Quando a massa está na posição x = + A, toda a energia é armazenada como energia potencial na mola U =\(\frac{1}{2}\) kA ². A energia cinética é igual a zero porque a velocidade da massa é zero. (b) À medida que a massa se move em direção a x = −A, a massa cruza a posição x = 0. Nesse ponto, a mola não é estendida nem comprimida, então a energia potencial armazenada na mola é zero. Em x = 0, a energia total é toda energia cinética onde K =\(\frac{1}{2}\) m (−v _max) ². (c) A massa continua a se mover até atingir x = −A, onde a massa para e começa a se mover em direção a x = + A. Na posição x = −A, a energia total é armazenada como energia potencial no comprimido U =\(\frac{1}{2}\) k (−A) ² e a energia cinética é zero. (d) À medida que a massa passa pela posição x = 0, a energia cinética é K =\(\frac{1}{2}\) mv _max ² e a energia potencial armazenada na mola é zero. (e) A massa retorna para a posição x = + A, onde K = 0 e U =\(\frac{1}{2}\) kA ².

Considere a Figura\(\PageIndex{1}\), que mostra a energia em pontos específicos do movimento periódico. Enquanto permanece constante, a energia oscila entre a energia cinética do bloco e a energia potencial armazenada na primavera:

\[E_{Total} = U + K = \frac{1}{2} kx^{2} + \frac{1}{2} mv^{2} \ldotp\]

O movimento do bloco em uma mola em SHM é definido pela posição x (t) = Acos\(\omega\) t +\(\phi\)) com uma velocidade de v (t) = −A\(\omega\) sin (\(\omega\)t +\(\phi\)). Usando essas equações, a identidade trigonométrica cos ²\(\theta\) + sin ²\(\theta\) = 1 e\(\omega = \sqrt{\frac{k}{m}}\), podemos encontrar a energia total do sistema:

\[\begin{split} E_{Total} & = \frac{1}{2} kA^{2} \cos^{2} (\omega t + \phi) + \frac{1}{2} mA^{2} \omega^{2} \sin^{2} (\omega t + \phi) \\ & = \frac{1}{2} kA^{2} \cos^{2} (\omega t + \phi) + \frac{1}{2} mA^{2} \left(\dfrac{k}{m}\right) \sin^{2} (\omega t + \phi) \\ & = \frac{1}{2} kA^{2} \cos^{2} (\omega t + \phi) + \frac{1}{2} kA^{2} \sin^{2} (\omega t + \phi) \\ & = \frac{1}{2} kA^{2} \cos^{2} (\omega t + \phi) + \frac{1}{2} mA^{2} \omega^{2} \sin^{2} (\omega t + \phi) \\ & = \frac{1}{2} kA^{2} (\cos^{2} (\omega t + \phi) + \sin^{2} (\omega t + \phi)) \\ & = \frac{1}{2} kA^{2} \ldotp \end{split}\]

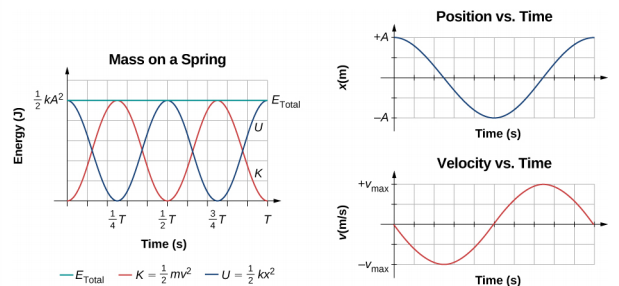
A energia total do sistema de um bloco e uma mola é igual à soma da energia potencial armazenada na mola mais a energia cinética do bloco e é proporcional ao quadrado da amplitude E _Total =\(\left(\dfrac{1}{2}\right)\) kA ². A energia total do sistema é constante.

Uma análise mais detalhada da energia do sistema mostra que a energia cinética oscila como uma função senoidal quadrada, enquanto a energia potencial oscila como uma função quadrada de cosseno. No entanto, a energia total do sistema é constante e proporcional ao quadrado da amplitude. A figura\(\PageIndex{2}\) mostra um gráfico das energias potenciais, cinéticas e totais do sistema de blocos e molas em função do tempo. Também estão representadas graficamente a posição e a velocidade em função do tempo. Antes do tempo t = 0,0 s, o bloco é preso à mola e colocado na posição de equilíbrio. O trabalho é feito no bloco aplicando uma força externa, puxando-o para uma posição de x = + A. O sistema agora tem energia potencial armazenada na mola. No tempo t = 0,00 s, a posição do bloco é igual à amplitude, a energia potencial armazenada na mola é igual a U =\(\frac{1}{2}\) kA ² e a força no bloco é máxima e aponta na direção x negativa (F _S = −kA). A velocidade e a energia cinética do bloco são zero no tempo t = 0,00 s. No tempo t = 0,00 s, o bloco é liberado do repouso.

Figura\(\PageIndex{2}\): Gráfico da energia cinética, energia potencial e energia total de um bloco oscilando em uma mola em SHM. Também são mostrados os gráficos de posição versus tempo e velocidade versus tempo. A energia total permanece constante, mas a energia oscila entre a energia cinética e a energia potencial. Quando a energia cinética é máxima, a energia potencial é zero. Isso ocorre quando a velocidade é máxima e a massa está na posição de equilíbrio. A energia potencial é máxima quando a velocidade é zero. A energia total é a soma da energia cinética mais a energia potencial e é constante.

Oscilações sobre uma posição de equilíbrio

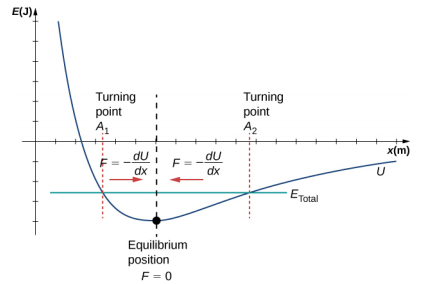
Acabamos de considerar a energia do SHM em função do tempo. Outra visão interessante do oscilador harmônico simples é considerar a energia como uma função da posição. A figura\(\PageIndex{3}\) mostra um gráfico da energia versus posição de um sistema submetido a SHM.

Figura\(\PageIndex{3}\): Um gráfico da energia cinética (vermelha), energia potencial (azul) e energia total (verde) de um oscilador harmônico simples. A força é igual a F = −\(\frac{dU}{dx}\). A posição de equilíbrio é mostrada como um ponto preto e é o ponto em que a força é igual a zero. A força é positiva quando x < 0, negative when x > 0 e igual a zero quando x = 0.

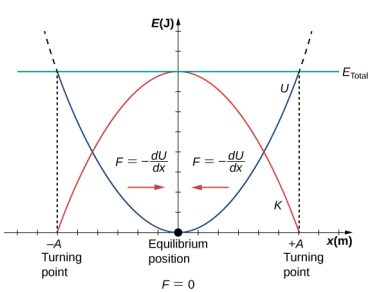
A curva de energia potencial na Figura\(\PageIndex{3}\) se assemelha a uma tigela. Quando uma bola de gude é colocada em uma tigela, ela se acomoda na posição de equilíbrio no ponto mais baixo da tigela (x = 0). Isso acontece porque uma força restauradora aponta para o ponto de equilíbrio. Esse ponto de equilíbrio às vezes é chamado de ponto fixo. Quando o mármore é deslocado para uma posição diferente (x = + A), o mármore oscila em torno da posição de equilíbrio. Olhando para o gráfico da energia potencial, a força pode ser encontrada observando a inclinação do gráfico de energia potencial (F = −\(\frac{dU}{dx}\)). Como a força em ambos os lados do ponto fixo aponta para trás em direção ao ponto de equilíbrio, o ponto de equilíbrio é chamado de ponto de equilíbrio estável. Os pontos x = A e x = −A são chamados de pontos de inflexão. (Veja Energia Potencial e Conservação de Energia.) A estabilidade é um conceito importante. Se um ponto de equilíbrio for estável, uma pequena perturbação de um objeto que esteja inicialmente no ponto de equilíbrio estável fará com que o objeto oscile em torno desse ponto. O ponto de equilíbrio estável ocorre porque a força em ambos os lados é direcionada para ele. Para um ponto de equilíbrio instável, se o objeto for ligeiramente perturbado, ele não retornará ao ponto de equilíbrio.

Considere o exemplo do mármore na tigela. Se a tigela estiver com o lado direito para cima, o mármore, se ligeiramente perturbado, oscilará em torno do ponto de equilíbrio estável. Se a tigela for virada de cabeça para baixo, a bola de gude pode ser balanceada na parte superior, no ponto de equilíbrio onde a força líquida é zero. No entanto, se a bola de gude for levemente perturbada, ela não retornará ao ponto de equilíbrio, mas sim sairá da tigela. A razão é que a força em ambos os lados do ponto de equilíbrio é direcionada para longe desse ponto. Esse ponto é um ponto de equilíbrio instável.

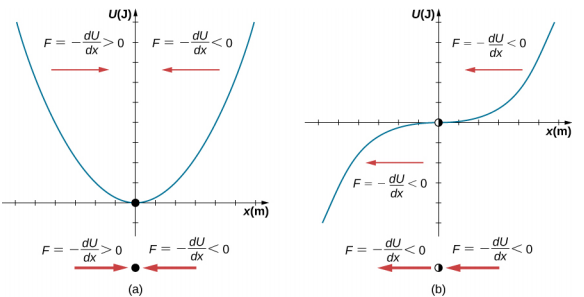
A figura\(\PageIndex{4}\) mostra três condições. O primeiro é um ponto de equilíbrio estável (a), o segundo é um ponto de equilíbrio instável (b) e o último também é um ponto de equilíbrio instável (c), porque a força em apenas um lado aponta para o ponto de equilíbrio.

Figura\(\PageIndex{4}\): Exemplos de pontos de equilíbrio. (a) Ponto de equilíbrio estável; (b) ponto de equilíbrio instável; (c) ponto de equilíbrio instável (às vezes chamado de ponto de equilíbrio meio estável).

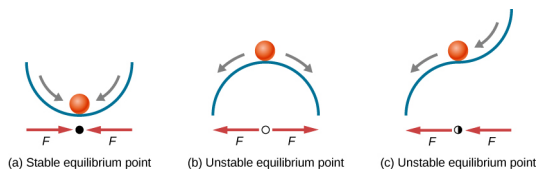
O processo de determinar se um ponto de equilíbrio é estável ou instável pode ser formalizado. Considere as curvas de energia potencial mostradas na Figura\(\PageIndex{5}\). A força pode ser encontrada analisando a inclinação do gráfico. A força é F = −\(\frac{dU}{dx}\). Em (a), o ponto fixo está em x = 0,00 m. Quando x < 0,00 m, a força é positiva. Quando x > 0,00 m, a força é negativa. Esse é um ponto estável. Em (b), o ponto fixo está em x = 0,00 m. Quando x < 0,00 m, a força é negativa. Quando x > 0,00 m, a força também é negativa. Esse é um ponto instável.

Figura\(\PageIndex{5}\): Dois exemplos de uma função de energia potencial. A força em uma posição é igual ao negativo da inclinação do gráfico nessa posição. (a) Uma função de energia potencial com um ponto de equilíbrio estável. (b) Uma função de energia potencial com um ponto de equilíbrio instável. Esse ponto às vezes é chamado de meio estável porque a força em um lado aponta para o ponto fixo.

Uma aplicação prática do conceito de pontos de equilíbrio estáveis é a força entre dois átomos neutros em uma molécula. Se duas moléculas estiverem próximas, separadas por alguns diâmetros atômicos, elas podem experimentar uma força atrativa. Se as moléculas se aproximarem o suficiente para que as camadas de elétrons dos outros elétrons se sobreponham, a força entre as moléculas se torna repulsiva. A força atrativa entre os dois átomos pode fazer com que os átomos formem uma molécula. A força entre as duas moléculas não é uma força linear e não pode ser modelada simplesmente como duas massas separadas por uma mola, mas os átomos da molécula podem oscilar em torno de um ponto de equilíbrio quando deslocados uma pequena quantidade da posição de equilíbrio. Os átomos oscilam devido à força atrativa e à força repulsiva entre os dois átomos.

Considere um exemplo da interação entre dois átomos conhecida como interação de van Der Waals. Está além do escopo deste capítulo discutir em profundidade as interações dos dois átomos, mas as oscilações dos átomos podem ser examinadas considerando um exemplo de modelo da energia potencial do sistema. Uma sugestão para modelar a energia potencial dessa molécula é com o potencial 6-12 de Lennard-Jones:

\[U(x) = 4 \epsilon \Bigg[ \left(\dfrac{\sigma}{x}\right)^{12} - \left(\dfrac{\sigma}{x}\right)^{6} \Bigg] \ldotp\]

Um gráfico dessa função é mostrado na Figura\(\PageIndex{6}\). Os dois parâmetros\(\epsilon\)\(\sigma\) são encontrados experimentalmente.

Figura\(\PageIndex{6}\): A função de energia potencial de Lennard-Jones para um sistema de dois átomos neutros. Se a energia estiver abaixo de alguma energia máxima, o sistema oscilará próximo da posição de equilíbrio entre os dois pontos de inflexão.

No gráfico, você pode ver que existe um poço de energia potencial, que tem algumas semelhanças com o poço de energia potencial da função de energia potencial do oscilador harmônico simples discutido na Figura\(\PageIndex{3}\). O potencial Lennard-Jones tem um ponto de equilíbrio estável onde a energia potencial é mínima e a força em ambos os lados do ponto de equilíbrio aponta para o ponto de equilíbrio. Observe que, diferentemente do oscilador harmônico simples, o poço potencial do potencial Lennard-Jones não é simétrico. Isso se deve ao fato de que a força entre os átomos não é uma força da lei de Hooke e não é linear. Os átomos ainda podem oscilar em torno da posição de equilíbrio x _min porque quando x < x _min, a força é positiva; quando x > x _min, a força é negativa. Observe que quando x se aproxima de zero, a inclinação é bastante íngreme e negativa, o que significa que a força é grande e positiva. Isso sugere que é necessária uma grande força para tentar aproximar os átomos. À medida que x se torna cada vez maior, a inclinação se torna menos íngreme e a força é menor e negativa. Isso sugere que, se receber uma energia grande o suficiente, os átomos podem ser separados.

Se você estiver interessado nessa interação, encontre a força entre as moléculas tomando a derivada da função de energia potencial. Você verá imediatamente que a força não se parece com a força da lei de Hooke (F = −kx), mas se você estiver familiarizado com o teorema binomial:

\[(1 + x)^{n} = 1 + nx + \frac{n(n - 1)}{2!} x^{2} + \frac{n(n - 1)(n - 2)}{3!} x^{3} + \cdots,\]

a força pode ser aproximada por uma força da lei de Hooke.

Velocidade e conservação de energia

Voltando ao sistema de um bloco e uma mola na Figura\(\PageIndex{1}\), uma vez que o bloco é liberado do repouso, ele começa a se mover na direção negativa em direção à posição de equilíbrio. A energia potencial diminui e a magnitude da velocidade e da energia cinética aumentam. No tempo t =\(\frac{T}{4}\), o bloco atinge a posição de equilíbrio x = 0,00 m, onde a força no bloco e a energia potencial são zero. Na posição de equilíbrio, o bloco atinge uma velocidade negativa com uma magnitude igual à velocidade máxima v = −A\(\omega\). A energia cinética é máxima e igual a K =\(\frac{1}{2}\) mv ² =\(\frac{1}{2}\) mA ² ω\(\omega^{2}\) =\(\frac{1}{2}\) kA ². Nesse ponto, a força no bloco é zero, mas o momento carrega o bloco e continua na direção negativa em direção a x = −A. À medida que o bloco continua se movendo, a força sobre ele age na direção positiva e a magnitude da velocidade e da energia cinética diminuem. A energia potencial aumenta à medida que a mola se comprime. No tempo t =\(\frac{T}{2}\), o bloco atinge x = −A. Aqui, a velocidade e a energia cinética são iguais a zero. A força no bloco é F = + kA e a energia potencial armazenada na mola é U =\(\frac{1}{2}\) kA ². Durante as oscilações, a energia total é constante e igual à soma da energia potencial e da energia cinética do sistema,

\[E_{Total} = \frac{1}{2} kx^{2} + \frac{1}{2} mv^{2} = \frac{1}{2} kA^{2} \ldotp \label{15.12}\]

A equação da energia associada ao SHM pode ser resolvida para encontrar a magnitude da velocidade em qualquer posição:

\[|v| = \sqrt{\frac{k}{m} (A^{2} - x^{2})} \ldotp \label{15.13}\]

A energia em um oscilador harmônico simples é proporcional ao quadrado da amplitude. Ao considerar muitas formas de oscilações, você encontrará a energia proporcional ao quadrado da amplitude.

Exercício 15.1

Por que doeria mais se você quebrasse a mão com uma régua do que com uma mola solta, mesmo que o deslocamento de cada sistema fosse igual?

Exercício 15.2

Identifique uma maneira de diminuir a velocidade máxima de um oscilador harmônico simples.