15.2: Movimento harmônico simples
- Page ID
- 185520
- Defina os termos período e frequência
- Liste as características do movimento harmônico simples
- Explicar o conceito de mudança de fase
- Escreva as equações de movimento para o sistema de uma massa e uma mola em movimento harmônico simples
- Descreva o movimento de uma massa oscilando em uma mola vertical
Quando você toca uma corda de guitarra, o som resultante tem um tom estável e dura muito tempo (Figura\(\PageIndex{1}\)). A corda vibra em torno de uma posição de equilíbrio e uma oscilação é concluída quando a corda começa da posição inicial, viaja para uma das posições extremas, depois para a outra posição extrema e retorna à sua posição inicial. Definimos movimento periódico como qualquer movimento que se repete em intervalos de tempo regulares, como exibido pela corda do violão ou por uma criança balançando em um balanço. Nesta seção, estudamos as características básicas das oscilações e sua descrição matemática.

Período e frequência em oscilações
Na ausência de atrito, o tempo para completar uma oscilação permanece constante e é chamado de período (T). Suas unidades geralmente são segundos, mas podem ser qualquer unidade de tempo conveniente. A palavra “período” se refere ao tempo de algum evento, seja repetitivo ou não, mas neste capítulo, trataremos principalmente do movimento periódico, que é, por definição, repetitivo.
Um conceito intimamente relacionado ao período é a frequência de um evento. A frequência (f) é definida como o número de eventos por unidade de tempo. Para movimentos periódicos, frequência é o número de oscilações por unidade de tempo. A relação entre frequência e período é
\[f = \frac{1}{T} \ldotp \label{15.1}\]
A unidade SI para frequência é o hertz (Hz) e é definida como um ciclo por segundo:
\[1\; Hz = 1\; cycle/sec\; or\; 1\; Hz = \frac{1}{s} = 1\; s^{-1} \ldotp\]
Um ciclo é uma oscilação completa
As máquinas de ultrassom são usadas por profissionais médicos para criar imagens para examinar os órgãos internos do corpo. Uma máquina de ultrassom emite ondas sonoras de alta frequência, que refletem nos órgãos, e um computador recebe as ondas, usando-as para criar uma imagem. Podemos usar as fórmulas apresentadas neste módulo para determinar a frequência, com base no que sabemos sobre oscilações. Considere um dispositivo de imagem médica que produz ultrassom oscilando com um período de 0,400\(\mu\) s. Qual é a frequência dessa oscilação?
Estratégia
O período (T) é dado e somos solicitados a encontrar a frequência (f).
Solução
Substitua 0,400 µs por T em f =\(\frac{1}{T}\):
\[f = \frac{1}{T} = \frac{1}{0.400 \times 10^{-6}\; s} \ldotp \nonumber\]
Resolva para encontrar
\[f = 2.50 \times 10^{6}\; Hz \ldotp \nonumber\]
Significância
Essa frequência de som é muito maior do que a frequência mais alta que os humanos podem ouvir (a faixa da audição humana é de 20 Hz a 20.000 Hz); portanto, é chamada de ultrassom. Oscilações apropriadas nessa frequência geram ultrassonografia usada para diagnósticos médicos não invasivos, como observações de um feto no útero.
Características do movimento harmônico simples
Um tipo muito comum de movimento periódico é chamado de movimento harmônico simples (SHM). Um sistema que oscila com o SHM é chamado de oscilador harmônico simples.
No movimento harmônico simples, a aceleração do sistema e, portanto, a força líquida, é proporcional ao deslocamento e atua na direção oposta ao deslocamento.
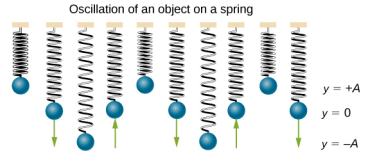
Um bom exemplo de SHM é um objeto com massa\(m\) presa a uma mola em uma superfície sem atrito, conforme mostrado na Figura\(\PageIndex{2}\). O objeto oscila em torno da posição de equilíbrio e a força líquida sobre o objeto é igual à força fornecida pela mola. Essa força obedece à lei de Hooke F s = −kx, conforme discutido em um capítulo anterior.
Se a força líquida pode ser descrita pela lei de Hooke e não há amortecimento (desaceleração devido ao atrito ou outras forças não conservadoras), então um oscilador harmônico simples oscila com igual deslocamento em ambos os lados da posição de equilíbrio, conforme mostrado para um objeto em uma mola na Figura \(\PageIndex{2}\). O deslocamento máximo do equilíbrio é chamado de amplitude (A). As unidades de amplitude e deslocamento são as mesmas, mas dependem do tipo de oscilação. Para o objeto na mola, as unidades de amplitude e deslocamento são metros.
O que há de tão significativo no SHM? Por um lado, o período\(T\) e a frequência\(f\) de um oscilador harmônico simples são independentes da amplitude. A corda de uma guitarra, por exemplo, oscila com a mesma frequência, seja puxada suavemente ou com força.
Dois fatores importantes afetam o período de um oscilador harmônico simples. O período está relacionado à rigidez do sistema. Um objeto muito rígido tem uma grande constante de força (k), o que faz com que o sistema tenha um período menor. Por exemplo, você pode ajustar a rigidez de uma prancha de mergulho: quanto mais rígida ela for, mais rápido ela vibra e menor será o período. O período também depende da massa do sistema oscilante. Quanto mais massivo for o sistema, maior será o período. Por exemplo, uma pessoa pesada em uma prancha de mergulho salta para cima e para baixo mais lentamente do que uma pessoa leve. De fato, a massa m e a constante de força k são os únicos fatores que afetam o período e a frequência do SHM. Para derivar uma equação para o período e a frequência, devemos primeiro definir e analisar as equações do movimento. Observe que a constante de força às vezes é chamada de constante de mola.
Equações do SHM
Considere um bloco preso a uma mola em uma mesa sem atrito (Figura\(\PageIndex{3}\)). A posição de equilíbrio (a posição em que a mola não está esticada nem comprimida) é marcada como x = 0. Na posição de equilíbrio, a força líquida é zero.
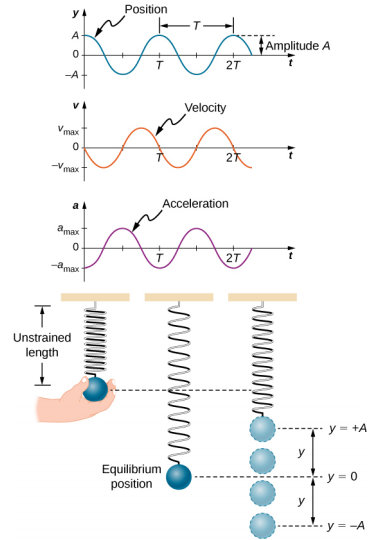
O trabalho é feito no bloco para retirá-lo para uma posição de x = + A e, em seguida, ele é liberado do repouso. A posição x máxima (A) é chamada de amplitude do movimento. O bloco começa a oscilar em SHM entre x = + A e x = −A, onde A é a amplitude do movimento e T é o período da oscilação. O período é o tempo de uma oscilação. A figura\(\PageIndex{4}\) mostra o movimento do bloco à medida que ele completa uma oscilação e meia após o lançamento.
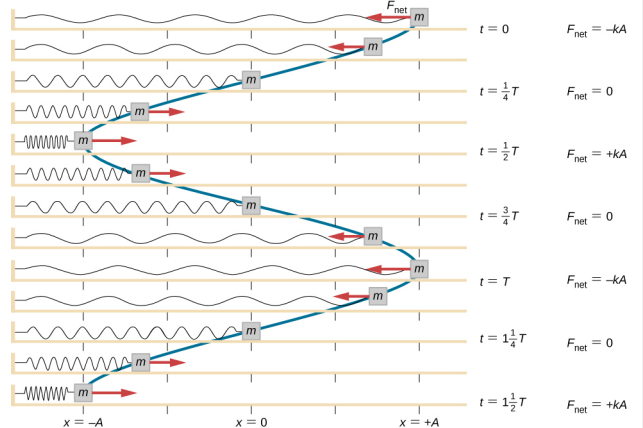
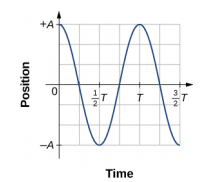
A figura\(\PageIndex{4}\) mostra um gráfico da posição do bloco em relação ao tempo. Quando a posição é plotada em relação ao tempo, fica claro que os dados podem ser modelados por uma função de cosseno com uma amplitude\(A\) e um período\(T\). A função cosseno cos\(\theta\) repete cada múltiplo de 2\(\pi\), enquanto o movimento do bloco se repete a cada período T. No entanto, a função\(\cos \left(\dfrac{2 \pi}{T} t \right)\) repete cada múltiplo inteiro do período. O máximo da função cosseno é um, então é necessário multiplicar a função cosseno pela amplitude A.
\[x(t) = A \cos \left(\dfrac{2 \pi}{T} t \right) = A \cos (\omega t) \ldotp \label{15.2}\]
Lembre-se do capítulo sobre rotação que a frequência angular é igual\(\omega = \frac{d \theta}{dt}\). Nesse caso, o período é constante, então a frequência angular é definida como 2\(\pi\) dividida pelo período,\(\omega = \frac{2 \pi}{T}\).
A equação da posição em função do tempo\(x(t) = A\cos( \omega t)\) é boa para modelar dados, onde a posição do bloco no momento inicial t = 0,00 s está na amplitude A e a velocidade inicial é zero. Freqüentemente, ao obter dados experimentais, a posição da massa no momento inicial t = 0,00 s não é igual à amplitude e a velocidade inicial não é zero. Considere 10 segundos de dados coletados por um aluno no laboratório, mostrados na Figura\(\PageIndex{6}\).
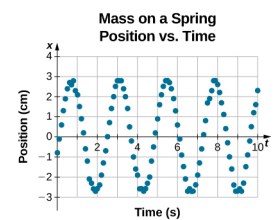
Os dados na Figura ainda\(\PageIndex{6}\) podem ser modelados com uma função periódica, como uma função de cosseno, mas a função é deslocada para a direita. Essa mudança é conhecida como mudança de fase e geralmente é representada pela letra grega phi (\(\phi\)). A equação da posição em função do tempo para um bloco em uma mola se torna
\[x(t) = A \cos (\omega t + \phi) \ldotp\]
Esta é a equação generalizada para SHM, onde t é o tempo medido em segundos,\(\omega\) é a frequência angular com unidades de segundos inversos, A é a amplitude medida em metros ou centímetros e\(\phi\) é a mudança de fase medida em radianos (Figura\(\PageIndex{7}\)). Deve-se notar que, como as funções seno e cosseno diferem apenas por uma mudança de fase, esse movimento pode ser modelado usando a função cosseno ou seno.
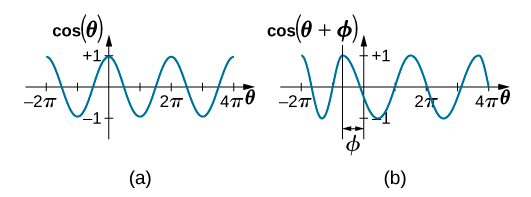
A velocidade da massa em uma mola, oscilando em SHM, pode ser encontrada tomando a derivada da equação de posição:
\[v(t) = \frac{dx}{dt} = \frac{d}{dt} (A \cos (\omega t + \phi)) = -A \omega \sin(\omega t + \varphi) = -v_{max} \sin (\omega t + \phi) \ldotp\]
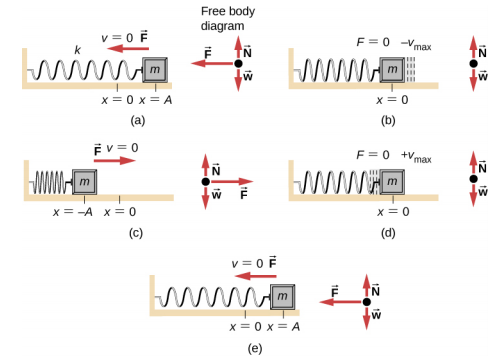
Como a função seno oscila entre —1 e +1, a velocidade máxima é a amplitude vezes a frequência angular, v max =\(\omega\) A. A velocidade máxima ocorre na posição de equilíbrio (x = 0) quando a massa está se movendo em direção a x = + A. A velocidade máxima na direção negativa é alcançada na posição de equilíbrio (x = 0) quando a massa está se movendo em direção a x = −A e é igual a −v max.
A aceleração da massa na mola pode ser encontrada tomando a derivada temporal da velocidade:
\[a(t) = \frac{dv}{dt} = \frac{d}{dt} (-A \omega \sin (\omega t + \phi)) = -A \omega^{2} \cos (\omega t + \varphi) = -a_{max} \cos (\omega t + \phi) \ldotp\]
A aceleração máxima é um máximo =\(\omega^{2}\) A. A aceleração máxima ocorre na posição (x = −A) e a aceleração na posição (x = −A) e é igual a −a max.
Resumo das equações de movimento para SHM
Em resumo, o movimento oscilatório de um bloco em uma mola pode ser modelado com as seguintes equações de movimento:
\[ \begin{align} x(t) &= A \cos (\omega t + \phi) \label{15.3} \\[4pt] v(t) &= -v_{max} \sin (\omega t + \phi) \label{15.4} \\[4pt] a(t) &= -a_{max} \cos (\omega t + \phi) \label{15.5} \end{align}\]
com
\[ \begin{align} x_{max} &= A \label{15.6} \\[4pt] v_{max} &= A \omega \label{15.7} \\[4pt] a_{max} &= A \omega^{2} \ldotp \label{15.8} \end{align}\]
Aqui,\(A\) é a amplitude do movimento,\(T\) é o período,\(\phi\) é a mudança de fase e\(\omega = \frac{2 \pi}{T}\) = 2\(\pi\) f é a frequência angular do movimento do bloco.
Um bloco de 2,00 kg é colocado em uma superfície sem atrito. Uma mola com uma força constante de k = 32,00 N/m é fixada ao bloco e a extremidade oposta da mola é fixada na parede. A mola pode ser comprimida ou estendida. A posição de equilíbrio é marcada como x = 0,00 m. O trabalho é feito no bloco, puxando-o para x = + 0,02 m. O bloco é liberado do repouso e oscila entre x = + 0,02 m e x = −0,02 m. O período do movimento é 1,57 s. Determine as equações do movimento.
Estratégia
Primeiro, encontramos a frequência angular. A mudança de fase é zero,\(\phi\) = 0,00 rad, porque o bloco é liberado do repouso em x = A = + 0,02 m. Uma vez encontrada a frequência angular, podemos determinar a velocidade máxima e a aceleração máxima.
Solução
A frequência angular pode ser encontrada e usada para encontrar a velocidade máxima e a aceleração máxima:
\[\begin{split} \omega & = \frac{2 \pi}{1.57\; s} = 4.00\; s^{-1}; \\ v_{max} & = A \omega = (0.02\; m)(4.00\; s^{-1}) = 0.08\; m/s; \\ a_{max} & = A \omega^{2} = (0.02; m)(4.00\; s^{-1})^{2} = 0.32\; m/s^{2} \ldotp \end{split}\]
Tudo o que resta é preencher as equações de movimento:
\[\begin{split} x(t) & = a \cos (\omega t + \phi) = (0.02\; m) \cos (4.00\; s^{-1} t); \\ v(t) & = -v_{max} \sin (\omega t + \phi) = (-0.8\; m/s) \sin (4.00\; s^{-1} t); \\ a(t) & = -a_{max} \cos (\omega t + \phi) = (-0.32\; m/s^{2}) \cos (4.00\; s^{-1} t) \ldotp \end{split}\]
Significância
A posição, a velocidade e a aceleração podem ser encontradas a qualquer momento. É importante lembrar que, ao usar essas equações, sua calculadora deve estar no modo radianos.
O período e a frequência de uma missa na primavera
Uma característica interessante do SHM de um objeto preso a uma mola é que a frequência angular e, portanto, o período e a frequência do movimento, dependem apenas da massa e da força constante, e não de outros fatores, como a amplitude do movimento. Podemos usar as equações do movimento e a segunda lei de Newton (\(\vec{F}_{net} = m \vec{a}\)) para encontrar equações para a frequência angular, frequência e período.
Considere o bloco em uma mola em uma superfície sem atrito. Existem três forças na massa: o peso, a força normal e a força devida à mola. As únicas duas forças que atuam perpendicularmente à superfície são o peso e a força normal, que têm magnitudes e direções opostas iguais e, portanto, somam zero. A única força que atua paralelamente à superfície é a força devida à mola, então a força líquida deve ser igual à força da mola:
\[\begin{split} F_{x} & = -kx; \\ ma & = -kx; \\ m \frac{d^{2} x}{dt^{2}} & = -kx; \\ \frac{d^{2} x}{dt^{2}} & = - \frac{k}{m} x \ldotp \end{split}\]
Substituir as equações do movimento por x e a nos dá
\[-A \omega^{2} \cos (\omega t + \phi) = - \frac{k}{m} A \cos (\omega t +\phi) \ldotp\]
Cancelando termos semelhantes e resolvendo os rendimentos de frequência angular
\[\omega = \sqrt{\frac{k}{m}} \ldotp \label{15.9}\]
A frequência angular depende apenas da força constante e da massa, e não da amplitude. A frequência angular é definida como\(\omega = \frac{2 \pi}{T}\), o que produz uma equação para o período do movimento:
\[T = 2 \pi \sqrt{\frac{m}{k}} \ldotp \label{15.10}\]
O período também depende apenas da massa e da força constante. Quanto maior a massa, maior o período. Quanto mais rígida a primavera, menor o período. A frequência é
\[f = \frac{1}{T} = \frac{1}{2 \pi} \sqrt{\frac{k}{m}} \ldotp \label{15.11}\]
Movimento vertical e uma mola horizontal
Quando uma mola é pendurada verticalmente e um bloco é preso e colocado em movimento, o bloco oscila em SHM. Nesse caso, não há força normal e o efeito líquido da força da gravidade é mudar a posição de equilíbrio. Considere a figura\(\PageIndex{8}\). Duas forças atuam no bloco: o peso e a força da mola. O peso é constante e a força da mola muda conforme o comprimento da mola muda.
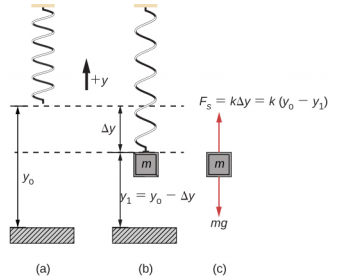
Quando o bloco atinge a posição de equilíbrio, como visto na Figura\(\PageIndex{8}\), a força da mola é igual ao peso do bloco, F net = F s − mg = 0, onde
\[-k (- \Delta y) = mg \ldotp\]
A partir da figura, a mudança na posição é\( \Delta y = y_{0}-y_{1} \) e\(-k (- \Delta y) = mg\), desde então, temos
\[k (y_{0} - y_{1}) - mg = 0 \ldotp\]
Se o bloco for deslocado e liberado, ele oscilará em torno da nova posição de equilíbrio. Conforme mostrado na Figura\(\PageIndex{9}\), se a posição do bloco for registrada em função do tempo, a gravação é uma função periódica. Se o bloco for deslocado para a posição y, a força líquida se torna F net = k (y 0 - y) − mg. Mas descobrimos que na posição de equilíbrio, mg = k\(\Delta\) y = ky 0 − ky 1. Substituir o peso na equação produz
\[F_{net} =ky_{0} - ky - (ky_{0} - ky_{1}) = k (y_{1} - y) \ldotp\]
Lembre-se de que y 1 é apenas a posição de equilíbrio e qualquer posição pode ser definida para ser o ponto y = 0,00 m. Então, vamos definir y 1 como y = 0,00 m. A força líquida então se torna
\[\begin{split}F_{net} & = -ky; \\ m \frac{d^{2} y}{dt^{2}} & = -ky \ldotp \end{split}\]
Isso é exatamente o que encontramos anteriormente para uma massa deslizante horizontalmente em uma mola. A força constante da gravidade serviu apenas para mudar a localização de equilíbrio da massa. Portanto, a solução deve ter a mesma forma de um bloco em uma mola horizontal, y (t) = Acos (\(\omega\)t +\(\phi\)). As equações para a velocidade e a aceleração também têm a mesma forma do caso horizontal. Observe que a inclusão da mudança de fase significa que o movimento pode realmente ser modelado usando uma função de cosseno ou seno, uma vez que essas duas funções diferem apenas por uma mudança de fase.