14.7: Dinâmica de fluidos

Last updated
Save as PDF

Page ID: 185636

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Descreva as características do fluxo
Calcular a taxa de fluxo
Descreva a relação entre vazão e velocidade
Explicar as consequências da equação de continuidade para a conservação da massa

A primeira parte deste capítulo tratou da estática dos fluidos, o estudo dos fluidos em repouso. O restante deste capítulo trata da dinâmica de fluidos, o estudo dos fluidos em movimento. Mesmo as formas mais básicas de movimento de fluidos podem ser bastante complexas. Por esse motivo, limitamos nossa investigação aos fluidos ideais em muitos dos exemplos. Um fluido ideal é um fluido com viscosidade insignificante. A viscosidade é uma medida do atrito interno em um fluido; nós a examinamos com mais detalhes em Viscosidade e Turbulência. Em alguns exemplos, examinamos um fluido incompressível — aquele para o qual é necessária uma força extremamente grande para alterar o volume — já que a densidade em um fluido incompressível é constante por toda parte.

Características do fluxo

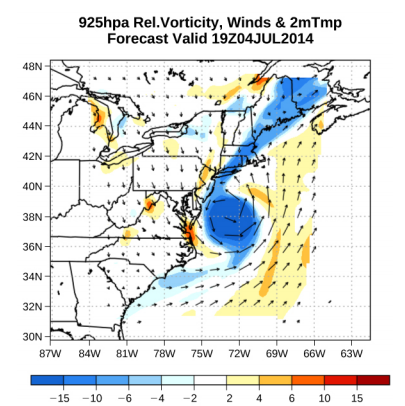
Os vetores de velocidade são frequentemente usados para ilustrar o movimento do fluido em aplicações como meteorologia. Por exemplo, o vento — o movimento fluido do ar na atmosfera — pode ser representado por vetores que indicam a velocidade e a direção do vento em qualquer ponto do mapa. A figura$\PageIndex{1}$ mostra vetores de velocidade descrevendo os ventos durante o furacão Arthur em 2014.

A figura é um mapa de pressão do furacão Arthur viajando pela costa leste. O centro de baixa pressão é indicado como o ponto azul. A velocidade do vento é mais alta perto do centro de baixa pressão, com os ventos se movendo no sentido anti-horário ao redor dele. — Figura$\PageIndex{1}$: Os vetores de velocidade mostram o fluxo do vento no furacão Arthur. Observe a circulação do vento ao redor do olho do furacão. As velocidades do vento são mais altas perto do olho. As cores representam a vorticidade relativa, uma medida de giro ou rotação do ar.

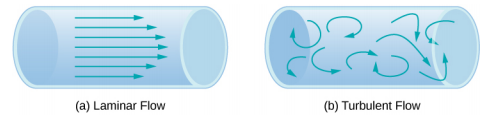
Outro método para representar o movimento do fluido é uma simplificação. Uma linha de fluxo representa o caminho de um pequeno volume de fluido à medida que ele flui. A velocidade é sempre tangencial à linha de fluxo. Os diagramas na Figura$\PageIndex{2}$ usam linhas aerodinâmicas para ilustrar dois exemplos de fluidos se movendo através de um tubo. O primeiro fluido exibe um fluxo laminar (às vezes descrito como um fluxo constante), representado por linhas de fluxo suaves e paralelas. Observe que no exemplo mostrado na parte (a), a velocidade do fluido é maior no centro e diminui perto das paredes do tubo devido à viscosidade do fluido e ao atrito entre as paredes do tubo e o fluido. Este é um caso especial de fluxo laminar, em que o atrito entre o tubo e o fluido é alto, conhecido como condições de limite sem deslizamento. O segundo diagrama representa um fluxo turbulento, no qual as linhas de fluxo são irregulares e mudam com o tempo. No fluxo turbulento, os caminhos do fluxo de fluido são irregulares à medida que diferentes partes do fluido se misturam ou formam pequenas regiões circulares que lembram banheiras de hidromassagem. Isso pode ocorrer quando a velocidade do fluido atinge uma determinada velocidade crítica.

A Figura A é o esquema do fluxo laminar mostrado como camadas de fluido se movendo em linhas paralelas. A Figura B é o esquema do fluxo turbulento mostrado como camadas de fluido se movendo em caminhos irregulares de colisão. — Figura$\PageIndex{2}$: (a) O fluxo laminar pode ser considerado como camadas de fluido se movendo em caminhos paralelos e regulares. (b) Em fluxo turbulento, regiões de fluido se movem em caminhos irregulares e de colisão, resultando em mistura e turbulência.

Taxa de fluxo e sua relação com a velocidade

O volume de fluido que passa por um determinado local através de uma área durante um período de tempo é chamado de taxa de fluxo$Q$, ou mais precisamente, taxa de fluxo volumétrico. Em símbolos, isso é escrito como

\[Q = \frac{dV}{dt} \label{14.13}\]

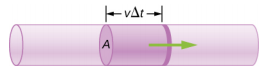
onde$V$ está o volume e$t$ é o tempo decorrido. Na Figura$\PageIndex{3}$, o volume do cilindro é$Ax$, então a vazão é

\[Q = \frac{dV}{dt} = \frac{d}{dt} (Ax) = A \frac{dx}{dt} = Av \ldotp\]

A unidade SI para vazão é m ³ /s, mas várias outras unidades$Q$ são de uso comum, como litros por minuto (L/min). Observe que um litro (L) é 1/1000 de um metro cúbico ou 1000 centímetros cúbicos (10 ⁻³ m ³ ou 10 ³ cm ³).

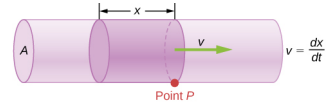
A figura é um esquema de uma tubulação uniforme com a área de seção transversal A. O fluido flui através da tubulação. O volume de fluido V passa um ponto P no tempo t. — Figura$\PageIndex{3}$: A taxa de fluxo é o volume de fluido que passa por um ponto através da área$A$ por unidade de tempo. Aqui, o cilindro sombreado de fluido passa pelo ponto$P$ em um tubo uniforme no tempo$t$.

A taxa de fluxo e a velocidade estão relacionadas, mas bem diferentes, quantidades físicas. Para deixar clara a distinção, considere a vazão de um rio. Quanto maior a velocidade da água, maior a vazão do rio. Mas a vazão também depende do tamanho e da forma do rio. Um rápido riacho de montanha carrega muito menos água do que o rio Amazonas no Brasil, por exemplo. A figura$\PageIndex{3}$ ilustra a taxa de fluxo de volume. A taxa de fluxo de volume é$Q = \frac{dV}{dt} = Av$, onde A é a área da seção transversal do tubo e v é a magnitude da velocidade.

A relação precisa entre a taxa de fluxo$Q$ e a velocidade média$v$ é

\[Q = Av,\]

onde$A$ está a área da seção transversal e$v$ é a velocidade média. A relação nos diz que a taxa de fluxo é diretamente proporcional à velocidade média do fluido e à área da seção transversal de um rio, tubo ou outro conduto. Quanto maior o conduíte, maior sua área de seção transversal. A figura$\PageIndex{3}$ ilustra como essa relação é obtida. O cilindro sombreado tem um volume$V = Ad$, que passa do ponto$P$ em um momento$t$. Dividindo os dois lados desse relacionamento por$t$ doações

\[\frac{V}{t} = \frac{Ad}{t} \ldotp \label{eq14.14A} \]

Notamos isso$Q = \frac{V}{t}$ e a velocidade média é$v = \frac{d}{t}$. Assim, a Equação\ ref {EQ14.14a} se torna

\[Q = Av.\]

A figura$\PageIndex{4}$ mostra um fluido incompressível fluindo ao longo de um tubo de raio decrescente. Como o fluido é incompressível, a mesma quantidade de fluido deve passar por qualquer ponto do tubo em um determinado momento para garantir a continuidade do fluxo. O fluxo é contínuo porque não são fontes ou sumidouros que adicionam ou removem massa, portanto, a massa que flui para o tubo deve ser igual à massa que sai do tubo. Nesse caso, como a área da seção transversal do tubo diminui, a velocidade deve necessariamente aumentar. Essa lógica pode ser estendida para dizer que a vazão deve ser a mesma em todos os pontos ao longo do tubo. Em particular, para os pontos arbitrários 1 e 2,

\[\begin{split} Q_{1} & = Q_{2}, \\ A_{1} v_{1} & = A_{2} v_{2} \ldotp \end{split} \label{14.14}\]

Isso é chamado de equação de continuidade e é válido para qualquer fluido incompressível (com densidade constante). As consequências da equação de continuidade podem ser observadas quando a água flui de uma mangueira para um bico de pulverização estreito: ela emerge com uma grande velocidade — esse é o propósito do bico. Por outro lado, quando um rio deságua em uma extremidade de um reservatório, a água diminui consideravelmente, talvez voltando a ganhar velocidade quando sai da outra extremidade do reservatório. Em outras palavras, a velocidade aumenta quando a área da seção transversal diminui e a velocidade diminui quando a área da seção transversal aumenta.

A figura é o esquema de uma tubulação que se estreita da área da seção transversal A1 para a área da seção transversal A2. O fluido flui pela tubulação. O volume de fluido V1 passa por um ponto 1, localizado na parte de seção transversal larga, no tempo t. O volume de fluido V2 passa por um ponto 2, localizado na parte estreita da seção transversal, no tempo t. — Figura$\PageIndex{4}$: Quando um tubo se estreita, o mesmo volume ocupa um comprimento maior. Para que o mesmo volume passe pelos pontos 1 e 2 em um determinado tempo, a velocidade deve ser maior no ponto 2. O processo é exatamente reversível. Se o fluido fluir na direção oposta, sua velocidade diminui quando o tubo se alarga. (Observe que os volumes relativos dos dois cilindros e as setas correspondentes do vetor de velocidade não são desenhados em escala.)

Como os líquidos são essencialmente incompressíveis, a equação da continuidade é válida para todos os líquidos. No entanto, os gases são compressíveis, portanto, a equação deve ser aplicada com cuidado aos gases se eles forem submetidos à compressão ou expansão.

Exemplo 14.5: Calculando a velocidade do fluido por meio de um bocal

Um bocal com diâmetro de 0,500 cm é conectado a uma mangueira de jardim com raio de 0,900 cm. A vazão através da mangueira e do bocal é de 0,500 L/s. Calcule a velocidade da água:

na mangueira e
no bocal.

Estratégia

Podemos usar a relação entre vazão e velocidade para encontrar as duas velocidades. Usamos o subscrito 1 para a mangueira e 2 para o bocal.

Solução

Resolvemos a equação da taxa de fluxo para velocidade e uso$\pi r_{1}^{2}$ para a área da seção transversal da mangueira, obtendo $$v =\ frac {Q} {A} =\ frac {Q} {\ pi r_ {1} ^ {2}\ ldotp$$ Substituir valores e usar conversões unitárias apropriadas produz $$v =\ frac {(0,500\; L/s) (10^ {-3}\; m^ {3} /L)} {(3,14) (9,00\ times 10^ {-3}\; m) ^ {2} } = 1,96\; m/s\ ldotp$$
Poderíamos repetir esse cálculo para encontrar a velocidade no bocal v ₂, mas usamos a equação da continuidade para fornecer uma visão um pouco diferente. A equação afirma $$A_ {1} v_ {1} = A_ {2} v_ {2}\ lDOTP$$Resolver por v ₂ e substituir$\pi r^{2}$ a área da seção transversal produz $$v_ {2} =\ frac {A_ {1}} {A_ {2}} v_ {1} =\ frac {\ pi r_ {1} ^ {2}} {\ pi r_ {2} ^ {2}} v_ {1} =\ frac {r_ {1} ^ {2}} {r_ {2} ^ {2}} v_ {1}\ ldotp$$ Substituindo valores conhecidos, $$v_ {2} =\ frac {(0,900\; cm) ^ {2}} {(0,250\; cm) ^ {2}} (1,96\; m/s) = 25,5\; m/s\ ldotp$$

Significância

Uma velocidade de 1,96 m/s é quase a certa para a água que sai de uma mangueira sem bico. O bocal produz um fluxo consideravelmente mais rápido simplesmente restringindo o fluxo para um tubo mais estreito.

A solução para a última parte do exemplo mostra que a velocidade é inversamente proporcional ao quadrado do raio do tubo, gerando grandes efeitos quando o raio varia. Podemos apagar uma vela a uma boa distância, por exemplo, apertando nossos lábios, enquanto soprar uma vela com a boca aberta é bastante ineficaz.

Conservação em massa

A taxa de fluxo de um fluido também pode ser descrita pela taxa de fluxo de massa ou taxa de fluxo de massa. Essa é a taxa na qual uma massa do fluido passa por um ponto. Consulte novamente a Figura$\PageIndex{3}$, mas desta vez considere a massa no volume sombreado. A massa pode ser determinada a partir da densidade e do volume:

\[m = \rho V = \rho Ax \ldotp\]

A taxa de fluxo de massa é então

\[\frac{dm}{dt} = \frac{d}{dt} (\rho Ax) = \rho A \frac{dx}{dt} = \rho Av,\]

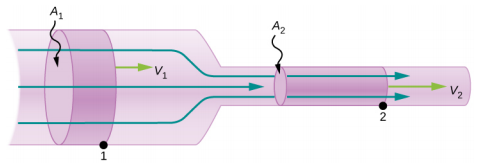
onde$\rho$ é a densidade, A é a área da seção transversal e v é a magnitude da velocidade. A taxa de fluxo de massa é uma quantidade importante na dinâmica de fluidos e pode ser usada para resolver muitos problemas. Considere a figura$\PageIndex{5}$. O tubo na figura começa na entrada com uma área de seção transversal de A ₁ e se contrai até uma saída com uma área de seção transversal menor de A ₂. A massa de fluido que entra no tubo deve ser igual à massa de fluido que sai do tubo. Por esse motivo, a velocidade na saída (v ₂) é maior que a velocidade da entrada (v ₁). Usando o fato de que a massa de fluido que entra no tubo deve ser igual à massa de fluido que sai do tubo, podemos encontrar uma relação entre a velocidade e a área da seção transversal calculando a taxa de variação da massa para dentro e para fora:

\[\begin{split} \left(\dfrac{dm}{dt}\right)_{1} & = \left(\dfrac{dm}{dt}\right)_{2} \\ \rho_{1} A_{1} v_{1} & = \rho_{2} A_{2} v_{2} \ldotp \end{split} \label{14.15}\]

A equação\ ref {14.15} também é conhecida como equação de continuidade na forma geral. Se a densidade do fluido permanecer constante durante a constrição, ou seja, se o fluido for incompressível, a densidade será cancelada da equação de continuidade,

\[A_{1} v_{1} = A_{2} v_{2} \ldotp\]

A equação se reduz para mostrar que a taxa de fluxo de volume no tubo é igual à taxa de fluxo de volume para fora do tubo.

A figura é um esquema do fluido fluindo em uma tubulação uniforme com a área de seção transversal A. O volume de fluido V delta t passa pela tubulação durante o tempo delta t. — Figura$\PageIndex{5}$: Geometria para derivar a equação de continuidade. A quantidade de líquido que entra na área da seção transversal (sombreada) deve ser igual à quantidade de líquido que sai da área da seção transversal se o líquido for incompressível.