14.8: Equação de Bernoulli

Objetivos de

• Explique os termos na equação de Bernoulli
• Explique como a equação de Bernoulli está relacionada à conservação de energia
• Descreva como derivar o princípio de Bernoulli da equação de Bernoulli
• Execute cálculos usando o princípio de Bernoulli
• Descreva algumas aplicações do princípio de Bernoulli

Como mostramos na Figura 14.7.4, quando um fluido flui para um canal mais estreito, sua velocidade aumenta. Isso significa que sua energia cinética também aumenta. O aumento da energia cinética vem do trabalho em rede realizado no fluido para empurrá-lo para o canal. Além disso, se o fluido mudar de posição vertical, o trabalho é feito no fluido pela força gravitacional.

Uma diferença de pressão ocorre quando o canal se estreita. Essa diferença de pressão resulta em uma força líquida no fluido porque a pressão vezes a área é igual à força, e essa força líquida funciona. Lembre-se do teorema trabalho-energia,

\[W_{net} = \frac{1}{2} mv^{2} - \frac{1}{2} mv_{0}^{2} \ldotp\]

O trabalho em rede realizado aumenta a energia cinética do fluido. Como resultado, a pressão cai em um fluido que se move rapidamente, independentemente de o fluido estar ou não confinado a um tubo.

Há muitos exemplos comuns de queda de pressão em fluidos que se movem rapidamente. Por exemplo, as cortinas do chuveiro têm o hábito desagradável de se encaixar no box do chuveiro quando o chuveiro está ligado. O motivo é que o fluxo de água e ar em alta velocidade cria uma região de menor pressão dentro do chuveiro, enquanto a pressão do outro lado permanece na pressão atmosférica padrão. Essa diferença de pressão resulta em uma força líquida, empurrando a cortina para dentro. Da mesma forma, quando um carro passa por um caminhão na rodovia, os dois veículos parecem puxar um em direção ao outro. O motivo é o mesmo: a alta velocidade do ar entre o carro e o caminhão cria uma região de menor pressão entre os veículos, e eles são unidos por uma pressão maior na parte externa (Figura\(\PageIndex{1}\)). Esse efeito foi observado em meados de 1800, quando se descobriu que os trens que passavam em direções opostas inclinavam-se precariamente um em direção ao outro.

Figura\(\PageIndex{1}\): Visão aérea de um carro passando por um caminhão em uma rodovia. O ar que passa entre os veículos flui em um canal mais estreito e deve aumentar sua velocidade (v2 é maior que v1), fazendo com que a pressão entre eles caia (pi é menor que po). Uma pressão maior do lado de fora empurra o carro e o caminhão juntos.

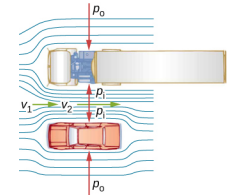
Conservação de energia e equação de Bernoulli

A aplicação do princípio de conservação de energia ao fluxo laminar sem atrito leva a uma relação muito útil entre pressão e velocidade de fluxo em um fluido. Essa relação é chamada de equação de Bernoulli, em homenagem a Daniel Bernoulli (1700-1782), que publicou seus estudos sobre movimento de fluidos em seu livro Hydrodynamica (1738).

Considere um fluido incompressível fluindo através de um tubo com diâmetro e altura variados, conforme mostrado na Figura\(\PageIndex{2}\). Os subscritos 1 e 2 na figura indicam dois locais ao longo do tubo e ilustram as relações entre as áreas das seções transversais A, a velocidade do fluxo v, a altura do solo y e a pressão p em cada ponto. Assumimos aqui que a densidade nos dois pontos é a mesma - portanto, a densidade é indicada por\(\rho\) sem nenhum subscrito - e, como o fluido é incompressível, os volumes sombreados devem ser iguais.

Figura\(\PageIndex{2}\): A geometria usada para a derivação da equação de Bernoulli.

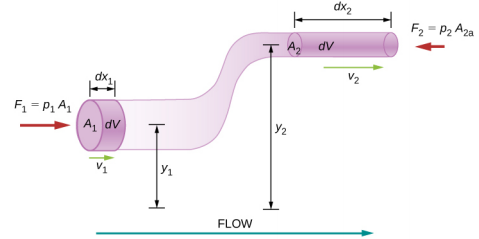
Também assumimos que não há forças viscosas no fluido, então a energia de qualquer parte do fluido será conservada. Para derivar a equação de Bernoulli, primeiro calculamos o trabalho que foi feito no fluido:

\[\begin{split} dW & = F_{1} dx_{1} - F_{2} dx_{2} \\ & = p_{1} A_{1} dx_{1} - p_{2} A_{2} dx_{2} \\ & = p_{1} dV - p_{2} dV = (p_{1} - p_{2}) dV \ldotp \end{split}\]

O trabalho realizado foi devido à força conservadora da gravidade e à mudança na energia cinética do fluido. A mudança na energia cinética do fluido é igual a

\[dK = \frac{1}{2} m_{2} v_{2}^{2} - \frac{1}{2} m_{1} v_{1}^{2} = \frac{1}{2} \rho dV (v_{2}^{2} - v_{1}^{2}) \ldotp\]

A mudança na energia potencial é

\[dU = mgy_{2} - mgy_{1} = \rho dV g(y_{2} - y_{1}) \ldotp\]

A equação da energia então se torna

\[\begin{split} dW & = dK + dU \\ (p_{1} - p_{2}) dV & = \frac{1}{2} \rho dV (v_{2}^{2} - v_{1}^{2}) + \rho dV g(y_{2} - y_{1}) \\ (p_{1} - p_{2}) & = \frac{1}{2} \rho (v_{2}^{2} - v_{1}^{2}) + \rho g(y_{2} - y_{1}) \ldotp \end{split}\]

Reorganizar a equação dá a equação de Bernoulli:

\[p_{1} + \frac{1}{2} \rho v_{1}^{2} + \rho gy_{1} = p_{2} + \frac{1}{2} \rho v_{2}^{2} + \rho gy_{2} \ldotp\]

Essa relação afirma que a energia mecânica de qualquer parte do fluido muda como resultado do trabalho realizado pelo fluido externo a essa parte, devido à variação da pressão ao longo do caminho. Como os dois pontos foram escolhidos arbitrariamente, podemos escrever a equação de Bernoulli de forma mais geral como um princípio de conservação ao longo do fluxo.

Equação de Bernoulli

Para um fluido incompressível e sem atrito, a combinação de pressão e a soma das densidades de energia cinética e potencial é constante não apenas ao longo do tempo, mas também ao longo de uma linha de fluxo:

\[p + \frac{1}{2} \rho v^{2} + \rho gy = constant \label{14.16}\]

Uma nota especial deve ser feita aqui sobre o fato de que, em uma situação dinâmica, as pressões na mesma altura em diferentes partes do fluido podem ser diferentes se tiverem velocidades de fluxo diferentes.

Analisando a equação de Bernoulli

De acordo com a equação de Bernoulli, se seguirmos um pequeno volume de fluido ao longo de seu caminho, várias quantidades na soma podem mudar, mas o total permanece constante. A equação de Bernoulli é, na verdade, apenas uma declaração conveniente de conservação de energia para um fluido incompressível na ausência de atrito.

A forma geral da equação de Bernoulli tem três termos e é amplamente aplicável. Para entendê-lo melhor, vamos considerar algumas situações específicas que simplificam e ilustram seu uso e significado.

Equação de Bernoulli para fluidos estáticos

Primeiro, considere a situação muito simples em que o fluido é estático, ou seja,\(v_1 = v_2 = 0\). A equação de Bernoulli nesse caso é

\[p_{1} + \rho gh_{1} = p_{2} + \rho gh_{2} \ldotp\]

Podemos simplificar ainda mais a equação definindo h ₂ = 0. (Qualquer altura pode ser escolhida para uma altura de referência de zero, como geralmente é feito para outras situações que envolvem força gravitacional, tornando todas as outras alturas relativas.) Nesse caso, obtemos

\[p_{2} = p_{1} + \rho gh_{1} \ldotp\]

Essa equação nos diz que, em fluidos estáticos, a pressão aumenta com a profundidade. À medida que vamos do ponto 1 ao ponto 2 no fluido, a profundidade aumenta em h ₁ e, consequentemente, p ₂ é maior que p ₁ em uma quantidade\(\rho gh_1\). No caso mais simples, p ₁ é zero na parte superior do fluido, e obtemos a relação familiar\(p = \rho gh\). (Lembre-se de que p =\(\rho gh\)\(\Delta Ug = −mgh\) e.) Assim, a equação de Bernoulli confirma o fato de que a mudança de pressão devido ao peso de um fluido é\(\rho gh\). Embora tenhamos introduzido a equação de Bernoulli para o movimento de fluidos, ela inclui muito do que estudamos anteriormente para fluidos estáticos.

Princípio de Bernoulli

Suponha que um fluido esteja se movendo, mas sua profundidade seja constante, ou seja,\(h_1 = h_2\). Sob essa condição, a equação de Bernoulli se torna

\[p_{1} + \frac{1}{2} \rho v_{1}^{2} = p_{2} + \frac{1}{2} \rho v_{2}^{2} \ldotp \label{Bernoulli}\]

Situações em que o fluido flui a uma profundidade constante são tão comuns que essa equação também é chamada de princípio de Bernoulli, que é simplesmente a equação de Bernoulli para fluidos em profundidade constante. (Observe novamente que isso se aplica a um pequeno volume de fluido à medida que o seguimos ao longo de seu caminho.) O princípio de Bernoulli reforça o fato de que a pressão cai à medida que a velocidade aumenta em um fluido em movimento: Se v ₂ for maior que v ₁ na equação, então p ₂ deve ser menor que p ₁ para que a igualdade se mantenha.

Exemplo 14.6: Calculando a pressão

No exemplo 14.5, descobrimos que a velocidade da água em uma mangueira aumentou de 1,96 m/s para 25,5 m/s indo da mangueira para o bocal. Calcule a pressão na mangueira, considerando que a pressão absoluta no bocal é 1,01 x 10 ⁵ N/m ² (atmosférica, como deve ser) e assumindo um fluxo nivelado e sem atrito.

Estratégia

Fluxo nivelado significa profundidade constante, então o princípio de Bernoulli se aplica. Usamos o subscrito 1 para valores na mangueira e 2 para aqueles no bocal. Portanto, somos solicitados a encontrar p ₁.

Solução

Resolvendo o princípio de Bernoulli (Equação Bernoulli) para\(p_1\) rendimentos

\[ \begin{align*} p_{1} &= p_{2} \frac{1}{2} \rho v_{2}^{2} - \frac{1}{2} \rho v_{1}^{2} \\[4pt] &= p_{2} + \frac{1}{2} \rho (v_{2}^{2} - v_{1}^{2}) \ldotp \end{align*}\]

Substituindo valores conhecidos,

\[\begin{align*} p_{1} & = (1.01 \times 10^{5}\; N/m^{2}) + \frac{1}{2} (10^{3}\; kg/m^{3})[(25.5\; m/s)^{2} - (1.96\; m/s)^{2}] \\[4pt] & = 4.24 \times 10^{5}\; N/m^{2} \ldotp \end{align*}\]

Significância

Essa pressão absoluta na mangueira é maior do que no bocal, como esperado, já que v é maior no bocal. A pressão p ₂ no bocal deve ser atmosférica, pois a água emerge na atmosfera sem outras alterações nas condições.

Aplicações do Princípio de Bernoulli

Muitos dispositivos e situações ocorrem nos quais o fluido flui a uma altura constante e, portanto, pode ser analisado com o princípio de Bernoulli.

Arrastamento

Há muito tempo que as pessoas colocam em prática o princípio de Bernoulli usando pressão reduzida em fluidos de alta velocidade para movimentar as coisas. Com uma pressão mais alta na parte externa, o fluido de alta velocidade força outros fluidos a entrarem no fluxo. Esse processo é chamado de arrastamento. Os dispositivos de arrastamento estão em uso desde a antiguidade como bombas para elevar a água a pequenas alturas, conforme necessário para drenar pântanos, campos ou outras áreas baixas. Alguns outros dispositivos que usam o conceito de arrastamento são mostrados na Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Os dispositivos de arrastamento usam maior velocidade do fluido para criar baixas pressões, que então arrastam um fluido para outro. (a) Um queimador Bunsen usa um bocal de gás ajustável, arrastando o ar para uma combustão adequada. (b) Um atomizador usa uma lâmpada de compressão para criar um jato de ar que arrasta gotas de perfume. Pulverizadores de tinta e carburadores usam técnicas muito semelhantes para mover seus respectivos líquidos. (c) Um aspirador comum usa um fluxo de água de alta velocidade para criar uma região de menor pressão. Os aspiradores podem ser usados como bombas de sucção em situações odontológicas e cirúrgicas ou para drenar um porão inundado ou produzir uma pressão reduzida em um vaso. (d) A chaminé de um aquecedor de água foi projetada para arrastar o ar para o tubo que passa pelo teto.

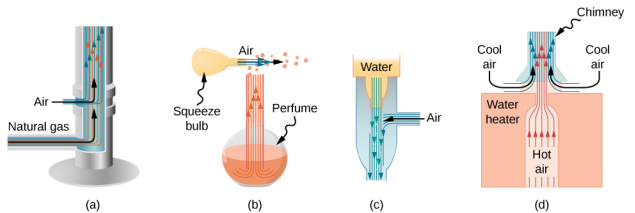
Medição de velocidade

A figura\(\PageIndex{4}\) mostra dois dispositivos que aplicam o princípio de Bernoulli para medir a velocidade do fluido. O manômetro na parte (a) é conectado a dois tubos que são pequenos o suficiente para não perturbar sensivelmente o fluxo. O tubo voltado para o fluido que se aproxima cria um ponto morto com velocidade zero (v ₁ = 0) à sua frente, enquanto o fluido que passa pelo outro tubo tem velocidade v ₂. Isso significa que o princípio de Bernoulli, conforme declarado em

\[p_{1} + \frac{1}{2} \rho v_{1}^{2} = p_{2} + \frac{1}{2} \rho v_{2}^{2}\]

torna-se

\[p_{1} = p_{2} + \frac{1}{2} \rho v_{2}^{2} \ldotp\]

Assim, a pressão p ₂ sobre a segunda abertura é reduzida em\(\frac{1}{2} \rho v_{2}^{2}\), então o fluido no manômetro aumenta em h no lado conectado à segunda abertura, onde

\[h \propto \frac{1}{2} \rho v_{2}^{2} \ldotp\]

(Lembre-se de que o símbolo\(\propto\) significa “proporcional a”.) Resolvendo para v ₂, vemos que

\[v_{2} \propto \sqrt{h} \ldotp\]

A parte (b) mostra uma versão desse dispositivo que é de uso comum para medir várias velocidades de fluido; esses dispositivos são frequentemente usados como indicadores de velocidade do ar em aeronaves.

Figura\(\PageIndex{4}\): Medição da velocidade do fluido com base no princípio de Bernoulli. (a) Um manômetro é conectado a dois tubos próximos e pequenos o suficiente para não perturbar o fluxo. O tubo 1 está aberto na extremidade voltada para o fluxo. Um ponto morto com velocidade zero é criado lá. O tubo 2 tem uma abertura na lateral, então o fluido tem uma velocidade v na abertura; assim, a pressão lá cai. A diferença de pressão no manômetro é\(\frac{1}{2} \rho v_{2}^{2}\), então h é proporcional\(\frac{1}{2} \rho v_{2}^{2}\) a. (b) Este tipo de dispositivo de medição de velocidade é um tubo Prandtl, também conhecido como tubo de pitot.

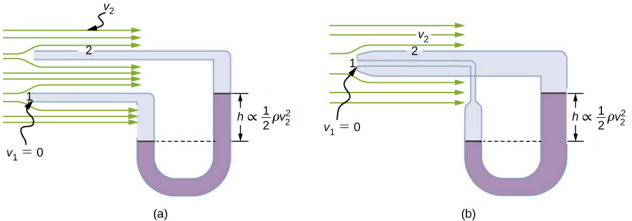
Uma mangueira de incêndio

Todas as aplicações anteriores da equação de Bernoulli envolviam condições simplificadas, como altura constante ou pressão constante. O próximo exemplo é uma aplicação mais geral da equação de Bernoulli, na qual pressão, velocidade e altura mudam.

Exemplo 14.7: Calculando a pressão - um bocal de mangueira de incêndio

As mangueiras de incêndio usadas em grandes incêndios estruturais têm um diâmetro interno de 6,40 cm (Figura\(\PageIndex{5}\)). Suponha que essa mangueira carregue um fluxo de 40,0 L/s, começando com uma pressão manométrica de 1,62 x 10 ⁶ N/m ². A mangueira sobe 10,0 m ao longo de uma escada até um bocal com um diâmetro interno de 3,00 cm. Qual é a pressão no bocal?

Figura\(\PageIndex{5}\): A pressão no bocal desta mangueira de incêndio é menor do que no nível do solo por dois motivos: a água tem que subir a colina para chegar ao bocal e a velocidade aumenta no bocal. Apesar de sua pressão baixa, a água pode exercer uma grande força sobre qualquer coisa que atinja em virtude de sua energia cinética. A pressão na corrente de água se torna igual à pressão atmosférica quando ela emerge no ar.

Estratégia

Devemos usar a equação de Bernoulli para resolver a pressão, já que a profundidade não é constante.

Solução

A equação de Bernoulli é

\[p_{1} + \frac{1}{2} \rho v_{1}^{2} + \rho gh_{1} = p_{2} + \frac{1}{2} \rho v_{2}^{2} + \rho gh_{2} \nonumber \]

onde os subscritos 1 e 2 se referem às condições iniciais ao nível do solo e às condições finais dentro do bocal, respectivamente. Devemos primeiro encontrar as velocidades v ₁ e v ₂. Como Q = A ₁ v ₁, obtemos

\[v_{1} = \frac{Q}{A_{1}} = \frac{40.0 \times 10^{-3}\; m^{3}/s}{\pi (3.20 \times 10^{-2}\; m)^{2}} = 12.4\; m/s \ldotp \nonumber\]

Da mesma forma, encontramos

\[v_{2} = 56.6\; m/s \ldotp \nonumber\]

Essa velocidade bastante grande é útil para alcançar o fogo. Agora, considerando h ₁ como zero, resolvemos a equação de Bernoulli para p ₂:

\[p_{2} = p_{1} + \frac{1}{2} \rho (v_{1}^{2} - v_{2}^{2}) - \rho gh_{2} \ldotp \nonumber\]

Substituir valores conhecidos rende

\[\begin{align*} p_{2} & = (1.62 \times 10^{6}\; N/m^{2}) + \frac{1}{2} (1000\; kg/m^{3}) [(12.4\; m/s)^{2} - (56.6\; m/s)^{2}] - (1000\; kg/m^{3})(9.80\; m/s^{2})(10.0\; m) \\ & = 0 \ldotp \end{align*}\]

Significância

Esse valor é uma pressão manométrica, pois a pressão inicial foi dada como uma pressão manométrica. Assim, a pressão do bocal é igual à pressão atmosférica necessária, porque a água sai para a atmosfera sem alterações em suas condições.