14.3: Fluidos, densidade e pressão (Parte 2)
- Page ID
- 185607
Variação da pressão com a profundidade em um fluido de densidade constante
A pressão é definida para todos os estados da matéria, mas é particularmente importante ao discutir fluidos. Uma característica importante dos fluidos é que não há resistência significativa ao componente de uma força aplicada paralelamente à superfície de um fluido. As moléculas do fluido simplesmente fluem para acomodar a força horizontal. Uma força aplicada perpendicularmente à superfície comprime ou expande o fluido. Se você tentar comprimir um fluido, descobrirá que uma força de reação se desenvolve em cada ponto dentro do fluido na direção externa, equilibrando a força aplicada nas moléculas no limite.
Considere um fluido de densidade constante, conforme mostrado na Figura\(\PageIndex{1}\). A pressão no fundo do recipiente é devida à pressão da atmosfera (p 0) mais a pressão devida ao peso do fluido. A pressão devida ao fluido é igual ao peso do fluido dividido pela área. O peso do fluido é igual à sua massa vezes a aceleração devido à gravidade.
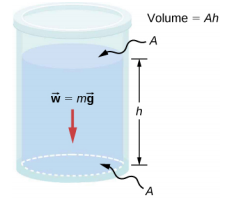
Como a densidade é constante, o peso pode ser calculado usando a densidade:
\[w = mg = \rho Vg = \rho Ahg \ldotp\]
A pressão no fundo do recipiente é, portanto, igual à pressão atmosférica adicionada ao peso do fluido dividido pela área:
\[p = p_{0} + \frac{\rho Ahg}{A} = p_{0} + \rho hg \ldotp\]
Essa equação só é boa para pressão em profundidade para um fluido de densidade constante
A pressão em profundidade em um fluido de densidade constante é igual à pressão da atmosfera mais a pressão devida ao peso do fluido, ou
\[p = p_{0} + \rho hg, \label{14.4}\]
Onde p é a pressão em uma determinada profundidade, p 0 é a pressão da atmosfera,\(\rho\) é a densidade do fluido, g é a aceleração devido à gravidade e h é a profundidade.

Considere a pressão e a força atuando na barragem que retém um reservatório de água (Figura\(\PageIndex{2}\)). Suponha que a barragem tenha 500 m de largura e a água tenha 80,0 m de profundidade na barragem, conforme ilustrado abaixo. (a) Qual é a pressão média na barragem devido à água? (b) Calcule a força exercida contra a barragem.
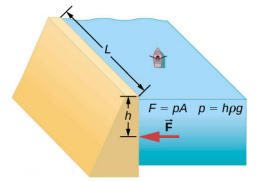
A pressão média p devido ao peso da água é a pressão na profundidade média h de 40,0 m, pois a pressão aumenta linearmente com a profundidade. A força exercida na barragem pela água é a pressão média vezes a área de contato, F = pA.
Solução
- A pressão média devido ao peso de um fluido é $$p = h\ rho g\ ldotp\ label {14.5} $$Inserindo a densidade da água da Tabela 14.1 e considerando h como a profundidade média de 40,0 m, obtemos $$\ begin {split} p & = (40,0\; m) (10^ {3}\; kg/m^ {3}) (9,80\; m/s/ ^ {2})\\ & = 3,92\ vezes 10^ {5}\; N/m^ {2} = 392\; kPa\ ldotp\ end {split} $$
- Já encontramos o valor para p. A área da barragem é $$A = (80,0\; m)\ times (500\; m) = 4,00\ times 10^ {4}\; m^ {2}\ ldotp$$so que $$\ begin {split} F & = (3,92\ times 10^ {5}\; N/m^ {2}) (4,00\ times 10^ {4}\; m^ {2})\\ & = 1,57\ times 10^ {10}\; M\ ldotp\ end {split} $$
Significância
Embora essa força pareça grande, ela é pequena em comparação com o peso de 1,96 x 10 13 N da água no reservatório. Na verdade, é apenas 0,0800% do peso.
Se o reservatório em Example\(\PageIndex{1}\) cobrisse o dobro da área, mas fosse mantido na mesma profundidade, a barragem precisaria ser redesenhada?
Pressão em um fluido estático em um campo gravitacional uniforme
Um fluido estático é um fluido que não está em movimento. Em qualquer ponto dentro de um fluido estático, a pressão em todos os lados deve ser igual — caso contrário, o fluido nesse ponto reagiria a uma força líquida e aceleraria.
A pressão em qualquer ponto de um fluido estático depende somente da profundidade nesse ponto. Conforme discutido, a pressão em um fluido próximo à Terra varia com a profundidade devido ao peso do fluido acima de um determinado nível. Nos exemplos acima, assumimos que a densidade é constante e que a densidade média do fluido é uma boa representação da densidade. Essa é uma aproximação razoável para líquidos como água, onde grandes forças são necessárias para comprimir o líquido ou alterar o volume. Em uma piscina, por exemplo, a densidade é aproximadamente constante e a água no fundo é comprimida muito pouco pelo peso da água no topo. Viajar na atmosfera é uma situação bem diferente, no entanto. A densidade do ar começa a mudar significativamente a uma curta distância acima da superfície da Terra.
Para derivar uma fórmula para a variação da pressão com a profundidade em um tanque contendo um fluido de densidade\(\rho\) na superfície da Terra, devemos começar com a suposição de que a densidade do fluido não é constante. O fluido localizado em níveis mais profundos é submetido a mais força do que o fluido mais próximo da superfície devido ao peso do fluido acima dele. Portanto, a pressão calculada em uma determinada profundidade é diferente da pressão calculada usando uma densidade constante.
Imagine um elemento fino de fluido a uma profundidade h, conforme mostrado na Figura\(\PageIndex{3}\). Deixe o elemento ter uma área de seção transversal A e altura\(\Delta\) y. As forças que atuam sobre o elemento são devidas às pressões p (y) acima e p (y +\(\Delta\) y) abaixo dele. O peso do elemento em si também é mostrado no diagrama de corpo livre.
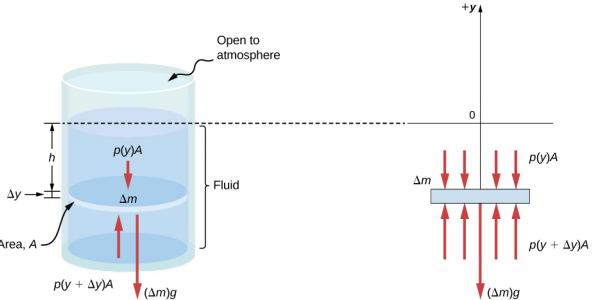
Como o elemento de fluido entre y e y +\(\Delta\) y não está acelerando, as forças são equilibradas. Usando um eixo y cartesiano orientado para cima, encontramos a seguinte equação para o componente y:
\[p(y + \Delta y)A - p(y)A - g \Delta m = 0(\Delta y < 0) \ldotp \label{14.6}\]
Observe que se o elemento tivesse um componente y de aceleração diferente de zero, o lado direito não seria zero, mas seria a massa vezes a aceleração y. A massa do elemento pode ser escrita em termos da densidade do fluido e do volume dos elementos:
\[\Delta m = |\rho A \Delta y| = - \rho A \Delta y \quad (\Delta y < 0) \ldotp\]
Colocando essa expressão para\(\Delta\) m na Equação\ ref {14.6} e depois dividindo os dois lados por A\(\Delta\) y, encontramos
\[\frac{p(y + \Delta y) - p(y)}{\Delta y} = - \rho g \ldotp \label{14.7}\]
Tomando o limite do elemento infinitesimalmente fino\(\Delta\) y → 0, obtemos a seguinte equação diferencial, que fornece a variação da pressão em um fluido:
\[\frac{dp}{dy} = - \rho g \ldotp \label{14.8}\]
Essa equação nos diz que a taxa de mudança de pressão em um fluido é proporcional à densidade do fluido. A solução dessa equação depende se a densidade\(\rho\) é constante ou muda com a profundidade; ou seja, a função\(\rho\) (y).
Se a faixa da profundidade que está sendo analisada não for muito grande, podemos supor que a densidade seja constante. Mas se a faixa de profundidade for grande o suficiente para que a densidade varie consideravelmente, como no caso da atmosfera, haverá uma mudança significativa na densidade com a profundidade. Nesse caso, não podemos usar a aproximação de uma densidade constante.
Pressão em um fluido com densidade constante
Vamos usar a Equação\ ref {14.9} para elaborar uma fórmula para a pressão a uma profundidade h da superfície em um tanque de um líquido, como água, onde a densidade do líquido pode ser considerada constante.
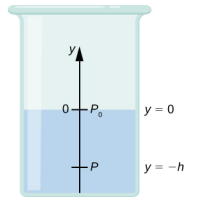
Precisamos integrar a Equação\ ref {14.9} de y = 0, onde a pressão é a pressão atmosférica (p 0), a y = −h, a coordenada y da profundidade:
\[\begin{split} \int_{p_{0}}^{p} dp & = - \int_{0}^{-h} \rho gdy \\ p - p_{0} & = \rho gh \\ p & = p_{0} + \rho gh \ldotp \end{split} \label{14.9}\]
Portanto, a pressão a uma profundidade de fluido na superfície da Terra é igual à pressão atmosférica mais\(\rho\) gh se a densidade do fluido for constante acima da altura, como descobrimos anteriormente.
Observe que a pressão em um fluido depende apenas da profundidade da superfície e não da forma do recipiente. Assim, em um recipiente onde um fluido pode se mover livremente em várias partes, o líquido permanece no mesmo nível em todas as partes, independentemente da forma, conforme mostrado na Figura\(\PageIndex{4}\).

Variação da pressão atmosférica com a altura
A mudança na pressão atmosférica com a altura é de particular interesse. Supondo que a temperatura do ar seja constante e que a lei dos gases ideais da termodinâmica descreva a atmosfera com uma boa aproximação, podemos encontrar a variação da pressão atmosférica com a altura, quando a temperatura é constante. (Discutimos a lei do gás ideal em um capítulo posterior, mas presumimos que você tenha alguma familiaridade com ela desde o ensino médio e a química.) Seja p (y) a pressão atmosférica na altura y. A densidade\(\rho\) em y, a temperatura T na escala Kelvin (K) e a massa m de uma molécula de ar estão relacionadas à pressão absoluta pela lei do gás ideal, na forma
\[p = \rho \frac{k_{B} T}{m}\; (atmosphere), \label{14.10}\]
onde k B é a constante de Boltzmann, que tem um valor de 1,38 x 10 −23 J/K.
Você pode ter encontrado a lei do gás ideal na forma pV = nRT, onde n é o número de moles e R é a constante do gás. Aqui, a mesma lei foi escrita de uma forma diferente, usando a densidade\(\rho\) em vez do volume V. Portanto, se a pressão p muda com a altura, a densidade também muda\(\rho\). Usando a densidade da lei do gás ideal, a taxa de variação da pressão com a altura é dada como
\[\frac{dp}{dy} = -p \left(\dfrac{mg}{k_{B} T}\right),\]
onde quantidades constantes foram coletadas entre parênteses. Substituindo essas constantes por um único símbolo\(\alpha\), a equação parece muito mais simples:
\[\begin{split} \frac{dp}{dy} & = - \alpha p \\ \frac{dp}{p} & = - \alpha dy \\ \int_{p_{0}}^{p(y)} \frac{dp}{p} & = \int_{0}^{y} - \alpha dy \\ [\ln (p)]_{p_{0}}^{p(y)} & = [- \alpha y]_{0}^{y} \\ \ln (p) - \ln (p_{0}) & = - \alpha y \\ \ln \left(\dfrac{p}{p_{0}}\right) & = - \alpha y \end{split}\]
Isso dá a solução
\[p(y) = p_{0} e^{- \alpha y} \ldotp\]
Assim, a pressão atmosférica cai exponencialmente com a altura, já que o eixo y é apontado para cima do solo e y tem valores positivos na atmosfera acima do nível do mar. A pressão cai em um fator de\(\frac{1}{e}\) quando a altura é\(\frac{1}{\alpha}\), o que nos dá uma interpretação física para\(\alpha\): A constante\(\frac{1}{\alpha}\) é uma escala de comprimento que caracteriza como a pressão varia com a altura e é frequentemente chamada de altura da escala de pressão.
Podemos obter um valor aproximado de\(\alpha\) usando a massa de uma molécula de nitrogênio como proxy para uma molécula de ar. À temperatura 27 °C, ou 300 K, encontramos
\[\alpha = - \frac{mg}{k_{B} T} = \frac{(4.8 \times 10^{-26}\; kg) \times (9.81\; m/s^{2})}{(1.38 \times 10^{-23}\; J/K) \times (300\; K)} = \frac{1}{8800\; m} \ldotp\]
Portanto, a cada 8800 metros, a pressão do ar cai em um fator 1/e, ou aproximadamente um terço de seu valor. Isso nos dá apenas uma estimativa aproximada da situação real, já que assumimos uma temperatura constante e um g constante em distâncias tão grandes da Terra, nenhuma das quais está correta na realidade.
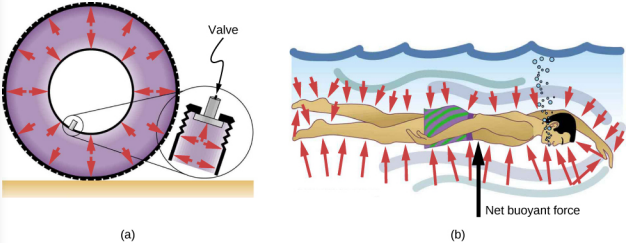
Direção da pressão em um fluido
A pressão do fluido não tem direção, sendo uma grandeza escalar, enquanto as forças devidas à pressão têm direções bem definidas: elas são sempre exercidas perpendicularmente a qualquer superfície. O motivo é que os fluidos não resistem nem exercem forças de cisalhamento. Assim, em um fluido estático encerrado em um tanque, a força exercida nas paredes do tanque é exercida perpendicularmente à superfície interna. Da mesma forma, a pressão é exercida perpendicularmente às superfícies de qualquer objeto dentro do fluido. A figura\(\PageIndex{5}\) ilustra a pressão exercida pelo ar nas paredes de um pneu e pela água no corpo de um nadador.