13.E: Gravitação (exercícios)

Perguntas conceituais

13.1 Lei da Gravitação Universal de Newton

1. Uma ação à distância, como é o caso da gravidade, já foi considerada ilógica e, portanto, falsa. Qual é o determinante final da verdade na ciência e por que essa ação à distância foi finalmente aceita?
2. Na lei da gravitação universal, Newton assumiu que a força era proporcional ao produto das duas massas (~m ₁ m ₂). Embora todas as conjecturas científicas devam ser verificadas experimentalmente, você pode fornecer argumentos sobre por que isso deve ser? (Você pode considerar exemplos simples em que qualquer outra forma levaria a resultados contraditórios.)

13.2 Gravitação perto da superfície da Terra

3. Os engenheiros devem levar em consideração a rotação da Terra ao construir edifícios muito altos em qualquer local que não seja o equador ou muito perto dos pólos?

13.3 Energia potencial gravitacional e energia total

4. Foi afirmado que um satélite com energia total negativa está em uma órbita limitada, enquanto um com energia total zero ou positiva está em uma órbita ilimitada. Por que isso é verdade? Que escolha de energia potencial gravitacional foi feita de forma que isso seja verdade?
5. Foi demonstrado que a energia necessária para elevar um satélite para uma órbita baixa da Terra (a mudança na energia potencial) é apenas uma pequena fração da energia cinética necessária para mantê-lo em órbita. Isso é verdade para órbitas maiores? Existe uma tendência para a proporção de energia cinética mudar na energia potencial à medida que o tamanho da órbita aumenta?

13.4 Órbitas e energia de satélites

6. Um estudante argumenta que um satélite em órbita está em queda livre porque o satélite continua caindo em direção à Terra. Outro diz que um satélite em órbita não está em queda livre porque a aceleração devido à gravidade não é de 9,80 m/s ². Com quem você concorda e por quê?
7. Muitos satélites são colocados em órbitas geossíncronas. O que há de especial nessas órbitas? Para uma rede de comunicação global, quantos desses satélites seriam necessários?

13.5 Leis do Movimento Planetário de Kepler

8. As leis do Kepler são puramente descritivas ou contêm informações causais?
9. No diagrama abaixo para um satélite em uma órbita elíptica em torno de uma massa muito maior, indique onde sua velocidade é maior e onde é a menor. Qual lei de conservação dita esse comportamento? Indique as direções da força, aceleração e velocidade nesses pontos. Desenhe vetores para essas mesmas três quantidades nos dois pontos em que o eixo y se cruza (ao longo do eixo semi-menor) e, a partir disso, determine se a velocidade está aumentando, diminuindo ou em um máximo/min.

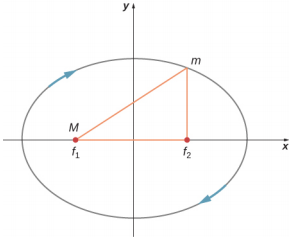
13.6 Forças de maré

10. Quando um objeto cai em um buraco negro, as forças das marés aumentam. Essas forças de maré sempre separarão o objeto quando ele se aproxima do raio de Schwarzschild? Como a massa do buraco negro e o tamanho do objeto afetam sua resposta?

13.7 Teoria da Gravidade de Einstein

11. O princípio da equivalência afirma que todos os experimentos feitos em um laboratório em um campo gravitacional uniforme não podem ser distinguidos daqueles feitos em um laboratório que não está em um campo gravitacional, mas está acelerando uniformemente. Para o último caso, considere o que acontece com um feixe de laser em alguma altura disparado perfeitamente horizontalmente no chão, através do laboratório de aceleração. (Veja isso de uma estrutura sem aceleração fora do laboratório.) Em relação à altura do laser, onde o feixe de laser atingirá a parede oposta? O que isso diz sobre o efeito de um campo gravitacional na luz? O fato de a luz não ter massa faz alguma diferença no argumento?
12. Quando uma pessoa se aproxima do raio Schwarzschild de um buraco negro, observadores externos veem todos os processos dessa pessoa (seus relógios, frequência cardíaca, etc.) diminuindo e parando ao atingir o raio de Schwarzschild. (A pessoa que cai no buraco negro vê seus próprios processos inalterados.) Mas a velocidade da luz é a mesma em todos os lugares para todos os observadores. O que isso diz sobre o espaço quando você se aproxima do buraco negro?

Problemas

13.1 Lei da Gravitação Universal de Newton

13. Avalie a magnitude da força gravitacional entre duas esferas esféricas de aço de 5 kg separadas por uma distância de centro a centro de 15 cm.
14. Estime a força gravitacional entre dois lutadores de sumô, com massas de 220 kg e 240 kg, quando são abraçados e seus centros estão separados por 1,2 m.
15. A astrologia define grande parte da posição dos planetas no momento do nascimento de alguém. A única força conhecida que um planeta exerce na Terra é a gravitacional. (a) Calcule a força gravitacional exercida em um bebê de 4,20 kg por um pai de 100 kg a 0,200 m de distância ao nascer (ele está ajudando, então está perto da criança). (b) Calcule a força sobre o bebê devido a Júpiter se ele estiver na distância mais próxima da Terra, a cerca de 6,29 x 10 ¹¹ m de distância. Como a força de Júpiter no bebê se compara à força do pai sobre o bebê? Outros objetos na sala e no prédio do hospital também exercem forças gravitacionais semelhantes. (É claro que pode haver uma força desconhecida atuando, mas primeiro os cientistas precisam se convencer de que existe até mesmo um efeito, muito menos do que uma força desconhecida o causa.)
16. Uma montanha a 10,0 km de uma pessoa exerce uma força gravitacional sobre ela igual a 2,00% de seu peso. (a) Calcule a massa da montanha. (b) Compare a massa da montanha com a da Terra. (c) O que não é razoável nesses resultados? (d) Quais premissas não são razoáveis ou inconsistentes? (Observe que medições gravitacionais precisas podem detectar facilmente o efeito de montanhas próximas e variações na geologia local.)
17. A Estação Espacial Internacional tem uma massa de aproximadamente 370.000 kg. (a) Qual é a força de uma astronauta adequada de 150 kg se ela estiver a 20 m do centro de massa da estação? (b) Quão precisa você acha que sua resposta seria?

Figura 13.33 (crédito: ©ESA—David Ducros)

18. O asteroide Toutatis passou perto da Terra em 2006 a quatro vezes a distância da nossa Lua. Essa foi a abordagem mais próxima que teremos até 2060. Se ele tem uma massa de 5,0 x 10 ¹³ kg, que força ele exerceu na Terra em sua aproximação mais próxima?
19. (a) Qual foi a aceleração da Terra causada pelo asteróide Toutatis (veja o problema anterior) em sua aproximação mais próxima? (b) Qual foi a aceleração de Toutatis nesse momento?

13.2 Gravitação perto da superfície da Terra

20. (a) Calcular a massa da Terra dada a aceleração devida à gravidade no Pólo Norte é medida em 9,832 m/s ² e o raio da Terra no polo é de 6356 km. (b) Compare isso com o valor da Ficha Técnica Terrestre da NASA de 5,9726 x 10 ²⁴ kg.
21. (a) Qual é a aceleração devida à gravidade na superfície da Lua? (b) Na superfície de Marte? A massa de Marte é 6,418 x 10 ²³ kg e seu raio é 3,38 x 10 ⁶ m.
22. (a) Calcule a aceleração devida à gravidade na superfície do Sol. (b) Por qual fator seu peso aumentaria se você pudesse ficar de pé no sol? (Não importa que você não possa.)
23. A massa de uma partícula é de 15 kg. (a) Qual é o seu peso na Terra? (b) Qual é o seu peso na Lua? (c) Qual é sua massa na Lua? (d) Qual é o seu peso no espaço sideral, longe de qualquer corpo celeste? (e) Qual é sua massa neste momento?
24. Em um planeta cujo raio é de 1,2 x 10 ⁷ m, a aceleração devido à gravidade é de 18 m/s ². Qual é a massa do planeta?
25. O diâmetro médio do planeta Saturno é 1,2 x 10 ⁸ m e sua densidade de massa média é 0,69 g/cm ³. Encontre a aceleração devida à gravidade na superfície de Saturno.
26. O diâmetro médio do planeta Mercúrio é 4,88 x 10 ⁶ m, e a aceleração devido à gravidade em sua superfície é de 3,78 m/s ². Estime a massa desse planeta.
27. A aceleração devido à gravidade na superfície de um planeta é três vezes maior do que na superfície da Terra. Sabe-se que a densidade de massa do planeta é o dobro da da Terra. Qual é o raio desse planeta em termos do raio da Terra?
28. Um corpo na superfície de um planeta com o mesmo raio da Terra pesa 10 vezes mais do que na Terra. Qual é a massa desse planeta em termos da massa da Terra?

13.3 Energia potencial gravitacional e energia total

29. Encontre a velocidade de fuga de um projétil da superfície de Marte.
30. Encontre a velocidade de fuga de um projétil da superfície de Júpiter.
31. Qual é a velocidade de escape de um satélite localizado na órbita da Lua em torno da Terra? Suponha que a lua não esteja próxima.
32. (a) Avalie a energia potencial gravitacional entre duas esferas esféricas de aço de 5,00 kg separadas por uma distância de centro a centro de 15,0 cm. (b) Supondo que ambos estejam inicialmente em repouso em relação um ao outro no espaço profundo, use a conservação de energia para descobrir a rapidez com que viajarão após o impacto. Cada esfera tem um raio de 5,10 cm.
33. Um asteróide de tamanho médio localizado a 5,0 x ^10,7 km da Terra com massa de 2,0 x 10 ¹³ kg é detectado indo diretamente em direção à Terra com velocidade de 2,0 km/s. Qual será sua velocidade logo antes de atingir nossa atmosfera? (Você pode ignorar o tamanho do asteróide.)
34. (a) Qual será a energia cinética do asteroide no problema anterior pouco antes de atingir a Terra? b) Compare essa energia com a produção da maior bomba de fissão, 2100 TJ. Que impacto isso teria na Terra?
35. (a) Qual é a mudança na energia de uma carga útil de 1000 kg retirada do repouso na superfície da Terra e colocada em repouso na superfície da Lua? (b) Qual seria a resposta se a carga útil fosse levada da superfície da Lua para a Terra? Esse é um cálculo razoável da energia necessária para mover uma carga útil para frente e para trás?

13.4 Órbitas e energia de satélites

36. Se um planeta com 1,5 vezes a massa da Terra estivesse viajando na órbita da Terra, qual seria seu período?
37. Dois planetas em órbitas circulares ao redor de uma estrela têm velocidades de v e 2v. (a) Qual é a proporção dos raios orbitais dos planetas? (b) Qual é a proporção de seus períodos?
38. Usando a distância média da Terra do Sol e o período orbital da Terra, (a) encontre a aceleração centrípeta da Terra em seu movimento em torno do Sol. (b) Compare esse valor com o da aceleração centrípeta no equador devido à rotação da Terra.
39. Qual é o raio orbital de um satélite da Terra com um período de 1,00 h? (b) O que não é razoável nesse resultado?
40. Calcule a massa do Sol com base nos dados da órbita da Terra e compare o valor obtido com a massa real do Sol.
41. Determine a massa de Júpiter com base no fato de que Io, sua lua mais interna, tem um raio orbital médio de 421.700 km e um período de 1,77 dias.
42. Observações astronômicas da nossa galáxia Via Láctea indicam que ela tem uma massa de cerca de 8,0 x 10 ¹¹ massas solares. Uma estrela orbitando na periferia da galáxia está a cerca de 6,0 x 10 ⁴ anos-luz de seu centro. (a) Qual deve ser o período orbital dessa estrela? (b) Se seu período for de 6,0 x 10 ⁷ anos, qual é a massa da galáxia? Esses cálculos são usados para sugerir a existência de outra matéria, como um buraco negro muito grande no centro da Via Láctea.
43. (a) Para evitar que um pequeno satélite caia em um asteróide próximo, ele é colocado em órbita com um período de 3,02 horas e raio de 2,0 km. Qual é a massa do asteróide? (b) Essa massa parece razoável para o tamanho da órbita?
44. A Lua e a Terra giram em torno de seu centro de massa comum, localizado a cerca de 4700 km do centro da Terra. (Isso é 1690 km abaixo da superfície.) (a) Calcule a aceleração devida à gravidade da Lua nesse ponto. (b) Calcule a aceleração centrípeta do centro da Terra à medida que ele gira em torno desse ponto uma vez a cada mês lunar (cerca de 27,3 d) e compare-a com a aceleração encontrada na parte (a). Comente se eles são iguais ou não e por que deveriam ou não ser.
45. O Sol orbita a galáxia Via Láctea uma vez a cada 2,60 x 10 ⁸ anos, com uma órbita aproximadamente circular com um raio médio de 3,00 x 10 ⁴ anos-luz. (Um ano-luz é a distância percorrida pela luz em 1 ano.) Calcule a aceleração centrípeta do Sol em sua órbita galáctica. Seu resultado apóia a alegação de que um quadro de referência quase inercial pode estar localizado no Sol? (b) Calcule a velocidade média do Sol em sua órbita galáctica. A resposta te surpreende?
46. Um satélite terrestre geossíncrono é aquele que tem um período orbital de exatamente 1 dia. Essas órbitas são úteis para comunicação e observação do tempo porque o satélite permanece acima do mesmo ponto na Terra (desde que orbite no plano equatorial na mesma direção da rotação da Terra). Calcule o raio dessa órbita com base nos dados da Terra no Apêndice D.

13.5 Leis do Movimento Planetário de Kepler

47. Calcule a massa do Sol com base nos dados da órbita média da Terra e compare o valor obtido com o valor comumente listado pelo Sol de 1,989 x 10 ³⁰ kg.
48. Io orbita Júpiter com um raio médio de 421.700 km e um período de 1.769 dias. Com base nesses dados, qual é a massa de Júpiter?
49. O raio orbital “médio” listado para objetos astronômicos que orbitam o Sol normalmente não é uma média integrada, mas é calculado de forma que forneça o período correto quando aplicado à equação para órbitas circulares. Diante disso, qual é o raio orbital médio em termos de afélio e periélio?
50. O periélio do cometa Halley é 0,586 UA e o afélio é 17,8 UA. Dado que sua velocidade no periélio é de 55 km/s, qual é a velocidade no afélio (1 AU = 1,496 x 10 ¹¹ m)? (Dica: Você pode usar a conservação de energia ou o momento angular, mas o último é muito mais fácil.)
51. O periélio do cometa Lagerkvist é de 2,61 UA e tem um período de 7,36 anos. Mostre que o afélio desse cometa é 4,95 UA.
52. Qual é a razão entre a velocidade no periélio e a do afélio do cometa Lagerkvist no problema anterior?
53. Eros tem uma órbita elíptica em torno do Sol, com uma distância do periélio de 1,13 UA e distância do afélio de 1,78 UA. Qual é o período de sua órbita?

13.6 Forças de maré

54. (a) Qual é a diferença entre as forças em uma massa de 1,0 kg no lado próximo de Io e no lado distante devido a Júpiter? Io tem um raio médio de 1821 km e um raio orbital médio em torno de Júpiter de 421.700 km. (b) Compare essa diferença com a calculada para a diferença da Terra devido à Lua calculada no Exemplo 13.14. As forças de maré são a causa da atividade vulcânica de Io.
55. Se o Sol colapsasse em um buraco negro, o ponto sem retorno para um investigador estaria a aproximadamente 3 km da singularidade central. O investigador conseguiria sobreviver visitando até 300 km do centro? Responda a isso descobrindo a diferença na atração gravitacional que os buracos negros exercem sobre uma massa de 1,0 kg na cabeça e nos pés do investigador.
56. Considere a Figura 13.23 em Tidal Forces. Este diagrama representa as forças de maré das marés da primavera. Esboce um diagrama semelhante para marés baixas. (Dica: Para simplificar, imagine que o Sol e a Lua contribuem igualmente. Seu diagrama seria a soma vetorial de dois campos de força (como na Figura 13.23), reduzida em um fator de dois e sobreposta em ângulos retos.)

13.7 Teoria da Gravidade de Einstein

57. Qual é o raio de Schwarzschild para o buraco negro no centro de nossa galáxia se ele tem a massa de 4 milhões de massas solares?
58. Qual seria o raio de Schwarzschild, em anos-luz, se nossa galáxia Via Láctea de 100 bilhões de estrelas colapsasse em um buraco negro? Compare isso com a nossa distância do centro, cerca de 13.000 anos-luz.

Problemas adicionais

59. Uma estrela de nêutrons é uma estrela fria e colapsada com densidade nuclear. Uma estrela de nêutrons em particular tem uma massa duas vezes maior que a do nosso Sol com um raio de 12,0 km. (a) Qual seria o peso de um astronauta de 100 kg em pé em sua superfície? (b) O que isso nos diz sobre pousar em uma estrela de nêutrons?
60. (a) A que distância do centro da Terra a força gravitacional líquida da Terra e da Lua em um objeto seria zero? (b) Definir as magnitudes das forças iguais deve resultar em duas respostas da quadrática. Você entende por que existem duas posições, mas apenas uma em que a força líquida é zero?
61. A que distância do centro do Sol a força gravitacional líquida da Terra e do Sol em uma nave espacial seria zero?
62. Calcule os valores de g na superfície da Terra para as seguintes mudanças nas propriedades da Terra: (a) sua massa é dobrada e seu raio é reduzido pela metade; (b) sua densidade de massa é dobrada e seu raio permanece inalterado; (c) sua densidade de massa é reduzida pela metade e sua massa permanece inalterada.
63. Suponha que você possa se comunicar com os habitantes de um planeta em outro sistema solar. Eles dizem que em seu planeta, cujo diâmetro e massa são 5,0 x 10 ³ km e 3,6 x 10 ²³ kg, respectivamente, o recorde de salto em altura é de 2,0 m. Dado que esse recorde está próximo a 2,4 m na Terra, o que você concluiria sobre a habilidade de pular de seus amigos extraterrestres?
64. (a) Suponha que seu peso medido no equador seja a metade do seu peso medido no polo de um planeta cuja massa e diâmetro sejam iguais aos da Terra. Qual é o período de rotação do planeta? (b) Você precisaria levar em consideração a forma desse planeta?
65. Um corpo de massa de 100 kg é pesado no Pólo Norte e no equador com uma balança de mola. Qual é a leitura da escala nesses dois pontos? Suponha que g = 9,83 m/s ² no polo.
66. Encontre a velocidade necessária para escapar do sistema solar partindo da superfície da Terra. Suponha que não haja outros corpos envolvidos e não leve em conta o fato de que a Terra está se movendo em sua órbita. [Dica: A equação 13.6 não se aplica. Use a Equação 13.5 e inclua a energia potencial da Terra e do Sol.
67. Considere o problema anterior e inclua o fato de que a Terra tem uma velocidade orbital em torno do Sol de 29,8 km/h s. (a) Qual velocidade em relação à Terra seria necessária e em que direção você deveria deixar a Terra? (b) Qual será a forma da trajetória?
68. Um cometa é observado a 1,50 UA do Sol com uma velocidade de 24,3 km/s. Este cometa está em uma órbita limitada ou não limitada?
69. Um asteróide tem velocidade de 15,5 km/s quando está localizado a 2,00 UA do sol. Em sua aproximação mais próxima, está a 0.400 UA do Sol. Qual é sua velocidade nesse ponto?
70. Detritos espaciais deixados por satélites antigos e seus lançadores estão se tornando um perigo para outros satélites. (a) Calcule a velocidade de um satélite em uma órbita 900 km acima da superfície da Terra. (b) Suponha que um rebite solto esteja em uma órbita do mesmo raio que cruza a órbita do satélite em um ângulo de 90°. Qual é a velocidade do rebite em relação ao satélite pouco antes de atingi-lo? (c) Se sua massa for de 0,500 g e ficar dentro do satélite, quanta energia em joules é gerada pela colisão? (Suponha que a velocidade do satélite não mude consideravelmente, porque sua massa é muito maior que a do rebite.)
71. Um satélite de massa de 1000 kg está em órbita circular em torno da Terra. O raio da órbita do satélite é igual a duas vezes o raio da Terra. (a) A que distância está o satélite? (b) Encontre a energia cinética, potencial e total do satélite.
72. Depois que Ceres foi promovido a planeta anão, agora reconhecemos que o maior asteroide conhecido é Vesta, com uma massa de 2,67 x 10 ²⁰ kg e um diâmetro variando de 578 km a 458 km. Supondo que Vesta seja esférica com raio de 520 km, determine a velocidade de escape aproximada de sua superfície.
73. (a) Usando os dados do problema anterior para o asteroide Vesta, qual seria o período orbital de uma sonda espacial em uma órbita circular de 10,0 km de sua superfície? (b) Por que esse cálculo é marginalmente útil, na melhor das hipóteses?
74. Qual é a velocidade orbital do nosso sistema solar em torno do centro da Via Láctea? Suponha que a massa dentro de uma esfera de raio igual à nossa distância do centro seja de cerca de 100 bilhões de massas solares. Nossa distância do centro é de 27.000 anos-luz.
75. (a) Usando as informações do problema anterior, de que velocidade você precisa para escapar da Via Láctea da nossa posição atual? (b) Você precisaria acelerar uma nave espacial a essa velocidade em relação à Terra?
76. As órbitas circulares na Equação 13.10 para seções cônicas devem ter excentricidade zero. A partir disso, e usando a segunda lei de Newton aplicada à aceleração centrípeta, mostre que o valor de α na Equação 13.10 é dado por\(\alpha = \frac{L^{2}}{GMm^{2}}\) onde L é o momento angular do corpo em órbita. O valor de α é constante e dado por essa expressão, independentemente do tipo de órbita.
77. Mostre que para excentricidade igual a um na Equação 13.10 para seções cônicas, o caminho é uma parábola. Faça isso substituindo as coordenadas cartesianas, x e y, pelas coordenadas polares, r e\(\theta\), e mostrando que ela tem a forma geral de uma parábola, x = ay ² + por + c.
78. Usando a técnica mostrada em Satellite Orbits and Energy, mostre que duas massas m ₁ e m ₂ em órbitas circulares em torno de seu centro de massa comum terão energia total\(E = K + E = K_{1} + k_{2} - \frac{Gm_{1} m_{2}}{r} = - \frac{G m_{1} m_{2}}{2r}\). Mostramos explicitamente a energia cinética de ambas as massas. (Dica: As massas orbitam em raios r ₁ e r ₂, respectivamente, onde r = r ₁ + r ₂. Certifique-se de não confundir o raio necessário para a aceleração centrípeta com o da força gravitacional.)
79. Dada a distância do periélio, p e a distância do afélio, q, para uma órbita elíptica, mostra que a velocidade no periélio, v _p, é dada por\(v_{p} = \sqrt{\frac{2GM_{Sun}}{(q + p)} \frac{q}{p}}\). (Dica: use a conservação do momento angular para relacionar v _p e v _q e, em seguida, substitua na equação de conservação de energia.)
80. O cometa P/1999 R1 tem um periélio de 0,0570 UA e um afélio de 4,99 UA. Usando os resultados do problema anterior, encontre sua velocidade no afélio. (Dica: A expressão é para o periélio. Use a simetria para reescrever a expressão para afélio.)

Problemas de desafio

81. Um túnel é cavado através do centro de um planeta perfeitamente esférico e sem ar de raio R. Usando a expressão para g derivada em Gravitação perto da superfície da Terra para obter uma densidade uniforme, mostre que uma partícula de massa m lançada no túnel executará um movimento harmônico simples. Deduza o período de oscilação de m e mostre que ele tem o mesmo período de uma órbita na superfície.
82. _{Seguindo a técnica usada em Gravitação perto da superfície da Terra, encontre o valor de g em função do raio r do centro de um planeta concha esférico de densidade constante\(\rho\) com raios internos e externos R dentro e R fora.} Encontre g para R _em < r < R _fora e para r < R _em. Supondo que o interior da concha seja mantido sem ar, descreva a viagem dentro do planeta concha esférico.
83. Mostre que a velocidade da área para uma órbita circular de raio r em torno de uma massa M é\(\frac{\Delta A}{\Delta t} = \frac{1}{2} \sqrt{GMr}\). Sua expressão fornece o valor correto da velocidade da área da Terra em torno do Sol?
84. Mostre que o período de órbita de duas massas, m ₁ e m ₂, em órbitas circulares de raios r ₁ e r ₂, respectivamente, em torno de seu centro de massa comum, é dado por\(T = 2 \pi \sqrt{\frac{r^{3}}{G(m_{1} + m_{2})}}\) onde r = r ₁ + r ₂. (Dica: As massas orbitam em raios r ₁ e r ₂, respectivamente, onde r = r ₁ + r ₂. Use a expressão para o centro de massa para relacionar os dois raios e observe que as duas massas devem ter momentos iguais, mas opostos. Comece com a relação do período com a circunferência e a velocidade da órbita de uma das massas. Use o resultado do problema anterior usando momenta nas expressões para a energia cinética.)
85. Mostre que para pequenas mudanças na altura h, como h << R _E, a Equação 13.4 se reduz à expressão\(\Delta\) U = mgh.
86. Usando a Figura 13.9, esboce cuidadosamente um diagrama de corpo livre para o caso de um pêndulo simples pendurado na latitude lambda, rotulando todas as forças que atuam na massa do ponto, m. Configure as equações de movimento para o equilíbrio, definindo uma coordenada na direção da aceleração centrípeta (em direção a P no diagrama), o outro perpendicular a isso. Mostre que o ângulo de deflexão\(\epsilon\), definido como o ângulo entre a corda do pêndulo e a direção radial em direção ao centro da Terra, é dado pela expressão abaixo. Qual é o ângulo de deflexão na latitude de 45 graus? Suponha que a Terra seja uma esfera perfeita. \(\tan(\lambda + \epsilon) = \frac{g}{(g − \omega^{2} R_{E})} \tan \lambda\), onde\(\omega\) está a velocidade angular da Terra.
87. (a) Mostre que a força de maré em um pequeno objeto de massa m, definida como a diferença na força gravitacional que seria exercida em m a uma distância no lado próximo e distante do objeto, devido à gravitação a uma distância R de M, é dada por F _tidal =\(\frac{2GMm}{R^{3}} \Delta\) r onde \(\Delta\)r é a distância entre o lado próximo e o lado distante e\(\Delta\) r << R. (b) Suponha que você esteja caindo primeiro no buraco negro no centro de nossa galáxia. Tem uma massa de 4 milhões de massas solares. Qual seria a diferença entre a força em sua cabeça e seus pés no raio de Schwarzschild (horizonte de eventos)? Suponha que seus pés e cabeça tenham massa de 5,0 kg e estejam separados por 2,0 m. Você sobreviveria passando pelo horizonte de eventos?
88. Encontre as velocidades de transferência de Hohmann,\(\Delta\) v _EllipseEarth e\(\Delta\) v _EllipseMars, necessárias para uma viagem a Marte. Use a Equação 13.7 para encontrar as velocidades orbitais circulares para a Terra e Marte. Usando a Equação 13.4 e a energia total da elipse (com semi-eixo maior a), dada por E = −\(\frac{GmM_{s}}{2a}\), determine as velocidades na Terra (periélio) e em Marte (afélio) necessárias para estar na elipse de transferência. A diferença,\(\Delta\) v, em cada ponto é o aumento de velocidade ou a velocidade de transferência necessária.

Contribuidores e atribuições

Template:ContribOpenStaxUni