13.6: Leis do movimento planetário de Kepler
- Page ID
- 184924
- Descreva as seções cônicas e como elas se relacionam com o movimento orbital
- Descreva como a velocidade orbital está relacionada à conservação do momento angular
- Determine o período de uma órbita elíptica a partir de seu eixo principal
Usando os dados precisos coletados por Tycho Brahe, Johannes Kepler analisou cuidadosamente as posições no céu de todos os planetas conhecidos e da Lua, traçando suas posições em intervalos regulares de tempo. A partir dessa análise, ele formulou três leis, que abordamos nesta seção.
Primeira Lei de Kepler
A visão predominante durante a época de Kepler era que todas as órbitas planetárias eram circulares. Os dados de Marte apresentaram o maior desafio a essa visão e acabaram encorajando Kepler a desistir da ideia popular. A primeira lei de Kepler afirma que todo planeta se move ao longo de uma elipse, com o Sol localizado no foco da elipse. Uma elipse é definida como o conjunto de todos os pontos de forma que a soma da distância de cada ponto até dois focos seja uma constante. A figura\(\PageIndex{1}\) mostra uma elipse e descreve uma maneira simples de criá-la.
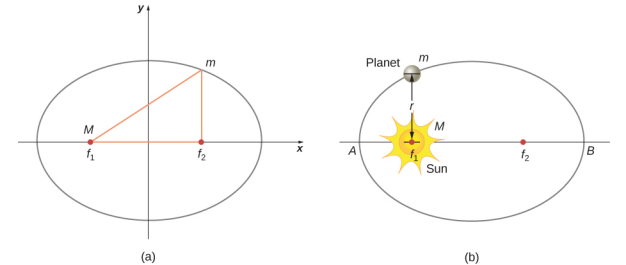
Para órbitas elípticas, o ponto de maior aproximação de um planeta ao Sol é chamado de periélio. É rotulado como ponto A na Figura\(\PageIndex{1}\). O ponto mais distante é o afélio e é rotulado como ponto B na figura. Para a órbita da Lua em torno da Terra, esses pontos são chamados de perigeu e apogeu, respectivamente.
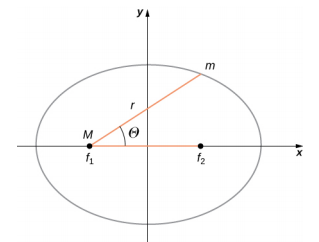
Uma elipse tem várias formas matemáticas, mas todas são um caso específico da equação mais geral para seções cônicas. Existem quatro seções cônicas diferentes, todas dadas pela equação
\[\frac{\alpha}{r} = 1 + e \cos \theta \ldotp \label{13.10}\]
As variáveis\(r\) e\(\theta\) são mostradas\(\PageIndex{2}\) na Figura no caso de uma elipse. As constantes α e e são determinadas pela energia total e pelo momento angular do satélite em um determinado ponto. A constante e é chamada de excentricidade. Os valores de\(\alpha\) e e determinam qual das quatro seções cônicas representa o caminho do satélite.
Um dos verdadeiros triunfos da lei da gravitação universal de Newton, com a força proporcional ao inverso da distância ao quadrado, é que, quando combinada com sua segunda lei, a solução para o caminho de qualquer satélite é uma seção cônica. Cada caminho percorrido por m é uma das quatro seções cônicas: um círculo ou uma elipse para órbitas limitadas ou fechadas, ou uma parábola ou hipérbole para órbitas abertas ou ilimitadas. Essas seções cônicas são mostradas na Figura\(\PageIndex{3}\).
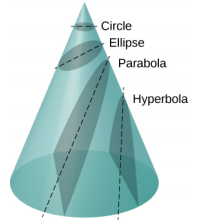
Se a energia total for negativa, então 0 ≤ e < 1, e a Equação\ ref {13.10} representa uma órbita limitada ou fechada de uma elipse ou círculo, onde e = 0. [Você pode ver na Equação 13.10 que para e = 0, r = e\(\alpha\), portanto, o raio é constante.] Para elipses, a excentricidade está relacionada à aparência oblonga da elipse. Um círculo tem excentricidade zero, enquanto uma elipse muito longa e estendida tem uma excentricidade próxima a uma.
Se a energia total for exatamente zero, então e = 1 e o caminho é uma parábola. Lembre-se de que um satélite com energia total zero tem exatamente a velocidade de escape. (A parábola é formada apenas cortando o cone paralelo à linha tangente ao longo da superfície.) Finalmente, se a energia total for positiva, então e > 1 e o caminho é uma hipérbole. Esses dois últimos caminhos representam órbitas ilimitadas, onde m passa por M uma vez e apenas uma vez. Essa situação foi observada em vários cometas que se aproximam do Sol e depois se afastam, para nunca mais voltarem.
Nós nos limitamos ao caso em que a menor massa (planeta) orbita uma massa muito maior e, portanto, estacionária (Sol), mas a Equação 13.10 também se aplica a quaisquer duas massas que interagem gravitacionalmente. Cada massa traça exatamente a mesma seção cônica da outra. Essa forma é determinada pela energia total e pelo momento angular do sistema, com o centro de massa do sistema localizado no foco. A proporção das dimensões dos dois caminhos é o inverso da razão de suas massas.
Você pode ver uma animação de dois objetos interagindo na página Meu Sistema Solar no PhET. Escolha a opção predefinida Sol e Planeta. Você também pode ver os problemas corporais múltiplos mais complicados. Você pode achar o caminho real da Lua bastante surpreendente, mas está obedecendo às simples leis do movimento de Newton.
Transferências orbitais
As pessoas imaginaram viajar para os outros planetas do nosso sistema solar desde que foram descobertos. Mas qual a melhor forma de fazer isso? O método mais eficiente foi descoberto em 1925 por Walter Hohmann, inspirado em um popular romance de ficção científica da época. O método agora é chamado de transferência de Hohmann. Para o caso de viajar entre duas órbitas circulares, a transferência ocorre ao longo de uma elipse de “transferência” que intercepta perfeitamente essas órbitas no afélio e no periélio da elipse. A figura\(\PageIndex{4}\) mostra o caso de uma viagem da órbita da Terra à de Marte. Como antes, o Sol está no foco da elipse.
Para qualquer elipse, o semi-eixo maior é definido como metade da soma do periélio e do afélio. Na Figura\(\PageIndex{4}\), o semi-eixo maior é a distância da origem até qualquer lado da elipse ao longo do eixo x, ou apenas metade do eixo mais longo (chamado eixo maior). Portanto, para viajar de uma órbita circular de raio r 1 para outra órbita circular de raio r 2, o afélio da elipse de transferência será igual ao valor da órbita maior, enquanto o periélio será a órbita menor. O semi-eixo maior, denotado a, é, portanto, dado por\(a = \frac{1}{2} (r_{1} + r_{2})\).
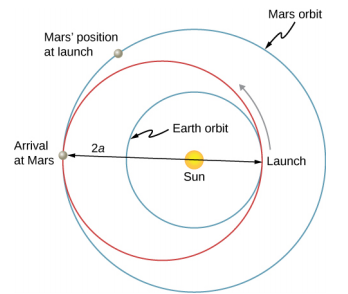
Vejamos o caso de viajar da Terra a Marte. No momento, ignoramos os planetas e assumimos que estamos sozinhos na órbita da Terra e desejamos passar para a órbita de Marte. A partir da Equação 13.9, expressão para energia total, podemos ver que a energia total de uma espaçonave na órbita maior (Marte) é maior (menos negativa) do que a da órbita menor (Terra). Para entrar na elipse de transferência da órbita da Terra, precisaremos aumentar nossa energia cinética, ou seja, precisamos de um aumento de velocidade. O método mais eficiente é uma aceleração muito rápida ao longo do caminho orbital circular, que também está ao longo do caminho da elipse nesse ponto. (Na verdade, a aceleração deve ser instantânea, de forma que as órbitas circular e elíptica sejam congruentes durante a aceleração. Na prática, a aceleração finita é curta o suficiente para que a diferença não seja uma consideração significativa.) Depois de chegar à órbita de Marte, você precisará de outro aumento de velocidade para entrar nessa órbita, ou permanecerá na órbita elíptica e simplesmente voltará para o periélio onde começou. Para a viagem de volta, basta reverter o processo com um impulso retroativo em cada ponto de transferência.
Para entrar na elipse de transferência e depois sair novamente, precisamos conhecer cada velocidade de órbita circular e as velocidades da órbita de transferência no periélio e no afélio. O aumento de velocidade necessário é simplesmente a diferença entre a velocidade da órbita circular e a velocidade da órbita elíptica em cada ponto. Podemos encontrar as velocidades orbitais circulares na Equação 13.7. Para determinar as velocidades da elipse, afirmamos sem provas (pois está além do escopo deste curso) que a energia total para uma órbita elíptica é
\[E = - \frac{GmM_{S}}{2a}\]
onde M S é a massa do Sol e a é o semi-eixo maior. Surpreendentemente, isso é o mesmo que a Equação 13.9 para órbitas circulares, mas com o valor do semi-eixo maior substituindo o raio orbital. Como conhecemos a energia potencial da Equação 13.4, podemos encontrar a energia cinética e, portanto, a velocidade necessária para cada ponto da elipse. Deixamos como um problema desafiador encontrar essas velocidades de transferência para uma viagem da Terra a Marte.
Encerramos essa discussão apontando alguns detalhes importantes. Primeiro, não contabilizamos a energia potencial gravitacional devida à Terra e a Marte, nem a mecânica do pouso em Marte. Na prática, isso deve fazer parte dos cálculos. Segundo, o tempo é tudo. Você não quer chegar à órbita de Marte para descobrir que ela não está lá. Devemos deixar a Terra exatamente na hora correta para que Marte esteja no afélio de nossa elipse de transferência assim que chegarmos. Essa oportunidade surge a cada 2 anos. E o retorno também requer um tempo correto. A viagem total levaria pouco menos de 3 anos! Existem outras opções que proporcionam um trânsito mais rápido, incluindo um sobrevoo de Vênus com assistência à gravidade. Mas essas outras opções trazem um custo adicional de energia e perigo para os astronautas.
Visite este site (https://openstaxcollege.org/l/21plantripmars) para obter mais detalhes sobre o planejamento de uma viagem a Marte.
Segunda Lei de Kepler
A segunda lei de Kepler afirma que um planeta varre áreas iguais em tempos iguais, ou seja, a área dividida pelo tempo, chamada de velocidade da área, é constante. Considere a figura\(\PageIndex{5}\). O tempo que um planeta leva para se mover da posição A para B, varrendo a área A 1, é exatamente o tempo necessário para se mover da posição C para D, varrendo a área A 2, e para se mover de E para F, varrendo a área A 3. Essas áreas são as mesmas: A 1 = A 2 = A 3.
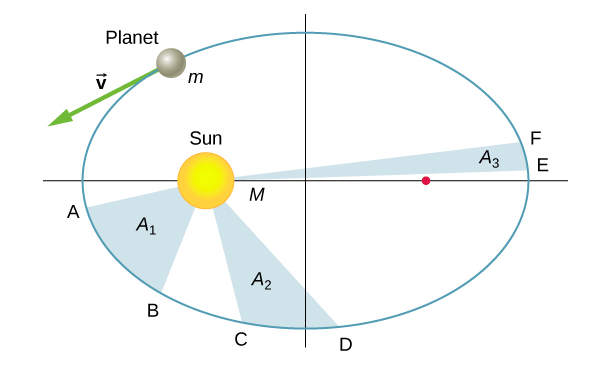
Comparando as áreas na figura e a distância percorrida ao longo da elipse em cada caso, podemos ver que, para que as áreas sejam iguais, o planeta deve acelerar à medida que se aproxima do Sol e desacelerar à medida que se afasta. Esse comportamento é completamente consistente com nossa equação de conservação, Equação\ ref {13.5}. Mas mostraremos que a segunda lei de Kepler é na verdade uma consequência da conservação do momento angular, que vale para qualquer sistema com apenas forças radiais.
Lembre-se da definição de momento angular a partir de Momento Angular,\(\vec{L} = \vec{r} \times \vec{p}\). Para o caso do movimento em órbita,\(\vec{L}\) é o momento angular do planeta em torno do Sol,\(\vec{r}\) é o vetor de posição do planeta medido a partir do Sol e\(\vec{p}\) = m\(\vec{v}\) é o momento linear instantâneo em qualquer ponto da órbita. Como o planeta se move ao longo da elipse,\(\vec{p}\) é sempre tangente à elipse.
Podemos resolver o momento linear em dois componentes: um componente radial\(\vec{p}_{rad}\) ao longo da linha até o Sol e um componente\(\vec{p}_{perp}\) perpendicular\(\vec{r}\) a. O produto cruzado do momento angular pode então ser escrito como
\[\begin{align*} \vec{L} &= \vec{r} \times \vec{p} \\[4pt] &= \vec{r} \times (\vec{p}_{rad} + \vec{p}_{perp}) \\[4pt] &= \vec{r} \times \vec{p}_{rad} + \vec{r} \times \vec{p}_{perp} \ldotp \end{align*}\]
O primeiro termo à direita é zero porque\(\vec{r}\) é paralelo a\(\vec{p}_{rad}\), e no segundo termo\(\vec{r}\) é perpendicular a\(\vec{p}_{perp}\), então a magnitude do produto cruzado se reduz para
\[L = rp_{perp} = rmv_{perp}.\]
Observe que o momento angular não depende de\(p_{rad}\). Como a força gravitacional está apenas na direção radial, ela só pode mudar\(p_{rad}\) e não\(p_{perp}\); portanto, o momento angular deve permanecer constante.
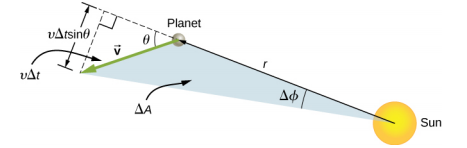
Agora considere a Figura\(\PageIndex{6}\). Uma pequena área triangular\(\Delta A\) é varrida com o tempo\(\Delta t\). A velocidade está ao longo do caminho e faz um ângulo\(\theta\) com a direção radial. Portanto, a velocidade perpendicular é dada por\(v_{perp}= v\sin \theta\). O planeta se move a uma distância\(\Delta\) s = v\(\Delta\) tsin\(\theta\) projetada ao longo da direção perpendicular\(r\) a. Como a área de um triângulo é metade da base (\(r\)) vezes a altura (\(\Delta s\)), para um pequeno deslocamento, a área é dada por
\[\Delta A = \frac{1}{2} r \Delta s. \nonumber\]
Substituindo por\(\Delta s\), multiplicando por\(m\) no numerador e no denominador e reorganizando, obtemos
\[\Delta A = \frac{1}{2} r \Delta s = \frac{1}{2} r (v \Delta t \sin \theta) = \frac{1}{2m} r (mv \sin \theta \Delta t) = \frac{1}{2m} r (mv_{perp} \Delta t) = \frac{L}{2m} \Delta t \ldotp\]
A velocidade da área é simplesmente a taxa de mudança da área com o tempo, então temos
\[ \text{areal velocity} = \frac{\Delta A}{\Delta t} = \frac{L}{2m} \ldotp\]
Como o momento angular é constante, a velocidade da área também deve ser constante. Essa é exatamente a segunda lei de Kepler. Assim como na primeira lei de Kepler, Newton mostrou que era uma consequência natural de sua lei da gravitação.
Você pode ver uma versão animada de Figure\(\PageIndex{6}\) e muitas outras animações interessantes no site da School of Physics (University of New South Wales).
Terceira Lei de Kepler
A terceira lei de Kepler afirma que o quadrado do período é proporcional ao cubo do semi-eixo maior da órbita. Em Órbitas e Energia de Satélite, derivamos a terceira lei de Kepler para o caso especial de uma órbita circular. A equação\ ref {13.8} nos dá o período de uma órbita circular de raio r sobre a Terra:
\[T = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} \ldotp \label{13.5.5}\]
Para uma elipse, lembre-se de que o semi-eixo maior é metade da soma do periélio e do afélio. Para uma órbita circular, o semi-eixo maior (\(a\)) é o mesmo que o raio da órbita. Na verdade, a Equação\ ref {13.5.5} nos dá a terceira lei de Kepler se simplesmente\(r\) substituirmos\(a\) e quadrarmos os dois lados.
\[T^{2} = \frac{4 \pi^{2}}{GM} a^{3} \label{13.11}\]
Mudamos a massa da Terra para a mais geral\(M\), já que essa equação se aplica aos satélites que orbitam qualquer massa grande.
Determine o semi-eixo maior da órbita do cometa Halley, já que ele chega ao periélio a cada 75,3 anos. Se o periélio é 0,586 UA, o que é o afélio?
Estratégia
Recebemos o período, então podemos reorganizar a Equação\ ref {13.11}, resolvendo para o semi-eixo maior. Como sabemos o valor do periélio, podemos usar a definição do semi-eixo maior, dada anteriormente nesta seção, para encontrar o afélio. Observamos que 1 Unidade Astronômica (UA) é o raio médio da órbita da Terra e está definida como 1 UA = 1,50 x 10 11 m.
Solução
Reorganizando a Equação\ ref {13.11} e inserindo os valores do período do cometa Halley e da massa do Sol, temos
\[\begin{split} a & = \left(\dfrac{GM}{4 \pi^{2}} T^{2}\right)^{1/3} \\ & = \left(\dfrac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(2.00 \times 10^{30}\; kg)}{4 \pi^{2}} (75.3\; yr \times 365\; days/yr \times 24\; hr/day \times 3600\; s/hr)^{2}\right)^{1/3} \ldotp \end{split}\]
Isso gera um valor de 2,67 x 10 12 m ou 17,8 UA para o semi-eixo maior. O semi-eixo maior é metade da soma do afélio e do periélio, então temos
\[\begin{split} a & = \frac{1}{2} (aphelion + perihelion) \\ aphelion & = 2a - perihelion \ldotp \end{split}\]
Substituindo os valores, encontramos o semi-eixo maior e o valor dado para o periélio, descobrimos que o valor do afélio é 35,0 UA.
Significância
Edmond Halley, contemporâneo de Newton, suspeitou pela primeira vez que três cometas, relatados em 1531, 1607 e 1682, eram na verdade o mesmo cometa. Antes de Tycho Brahe fazer medições de cometas, acreditava-se que eles eram eventos únicos, talvez distúrbios na atmosfera, e que não foram afetados pelo Sol. Halley usou a nova mecânica de Newton para prever o retorno de seu cometa homônimo em 1758.
A órbita quase circular de Saturno tem um raio médio de cerca de 9,5 UA e tem um período de 30 anos, enquanto Urano tem uma média de cerca de 19 UA e tem um período de 84 anos. Isso é consistente com nossos resultados para o cometa Halley?


