13.5: Órbitas e energia de satélites
- Page ID
- 184869
- Descreva o mecanismo das órbitas circulares
- Encontre os períodos orbitais e as velocidades dos satélites
- Determine se os objetos estão ligados gravitacionalmente
A Lua orbita a Terra. Por sua vez, a Terra e os outros planetas orbitam o Sol. O espaço diretamente acima da nossa atmosfera está cheio de satélites artificiais em órbita. Examinamos a mais simples dessas órbitas, a órbita circular, para entender a relação entre a velocidade e o período dos planetas e satélites em relação às suas posições e aos corpos que orbitam.
Órbitas circulares
Conforme observado no início deste capítulo, Nicolaus Copernicus sugeriu pela primeira vez que a Terra e todos os outros planetas orbitam o Sol em círculos. Ele ainda observou que os períodos orbitais aumentaram com a distância do Sol. Uma análise posterior de Kepler mostrou que essas órbitas são na verdade elipses, mas as órbitas da maioria dos planetas do sistema solar são quase circulares. A distância orbital da Terra em relação ao Sol varia apenas 2%. A exceção é a órbita excêntrica de Mercúrio, cuja distância orbital varia quase 40%.
Determinar a velocidade orbital e o período orbital de um satélite é muito mais fácil para órbitas circulares, então fazemos essa suposição na derivação a seguir. Conforme descrevemos na seção anterior, um objeto com energia total negativa está gravitacionalmente ligado e, portanto, está em órbita. Nosso cálculo para o caso especial de órbitas circulares confirmará isso. Nós nos concentramos em objetos que orbitam a Terra, mas nossos resultados podem ser generalizados para outros casos.
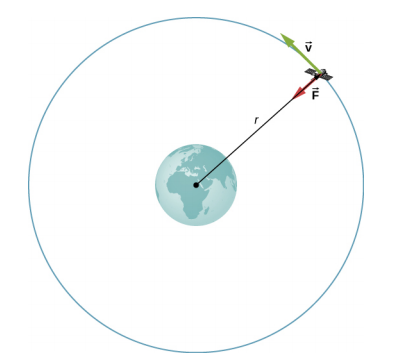
Considere um satélite de massa m em uma órbita circular em torno da Terra a uma\(r\) distância do centro da Terra (Figura\(\PageIndex{1}\)). Tem aceleração centrípeta direcionada para o centro da Terra. A gravidade da Terra é a única força atuando, então a segunda lei de Newton dá
\[\frac{GmM_{E}}{r^{2}} = ma_{c} = \frac{mv_{orbit}^{2}}{r} \ldotp\]
Resolvemos a velocidade da órbita, observando que\(m\) cancela, para obter a velocidade orbital
\[v_{orbit} = \sqrt{\frac{GM_{E}}{r}} \ldotp \label{13.7}\]
Consistente com o que vimos em\(g = G \frac{M_E}{r^2}\) e\(v_{esc} = \sqrt{\frac{2GM}{R}}\), m não aparece na Equação\ ref {13.7}. O valor de g, a velocidade de escape e a velocidade orbital dependem apenas da distância do centro do planeta, e não da massa do objeto que está sendo acionado. Observe a semelhança nas equações para a órbita v e v esc. A velocidade de escape é exatamente\(\sqrt{2}\) vezes maior, cerca de 40%, do que a velocidade orbital. Essa comparação foi observada no Exemplo 13.4.2 e é verdadeira para um satélite em qualquer raio.
Para encontrar o período de uma órbita circular, notamos que o satélite percorre a circunferência da órbita\( 2\pi r\) em um período\(T\). Usando a definição de velocidade, temos
\[v_{orbit} = \frac{2 \pi r}{T}.\]
Substituímos isso na Equação\ ref {13.7} e reorganizamos para obter
\[T = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} \ldotp \label{13.8}\]
Vemos na próxima seção que isso representa a terceira lei de Kepler para o caso de órbitas circulares. Também confirma a observação de Copérnico de que o período de um planeta aumenta com o aumento da distância do Sol. Só precisamos\(M_E\) substituir por\(M_{Sun}\) na Equação\ ref {13.8}.
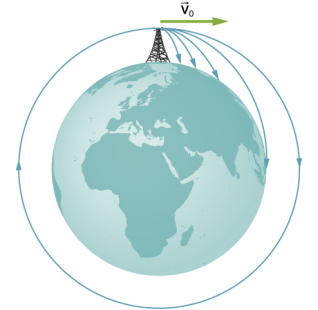
Concluímos esta seção retornando à nossa discussão anterior sobre astronautas em órbita que parecem não ter peso, como se estivessem caindo livremente em direção à Terra. Na verdade, eles estão em queda livre. Considere as trajetórias mostradas na Figura\(\PageIndex{2}\). (Essa figura é baseada em um desenho de Newton em seu Principia e também apareceu anteriormente em Motion in Two and Three Dimensions.) Todas as trajetórias mostradas que atingem a superfície da Terra têm menos que a velocidade orbital. Os astronautas acelerariam em direção à Terra ao longo dos caminhos não circulares mostrados e se sentiriam sem peso. (Na verdade, os astronautas treinam para viver em órbita andando em aviões que caem livremente por 30 segundos de cada vez.) Mas com a velocidade orbital correta, a superfície da Terra se curva para longe deles exatamente na mesma taxa em que caem em direção à Terra. Obviamente, ficar à mesma distância da superfície é o ponto de uma órbita circular.
Podemos resumir nossa discussão sobre satélites em órbita na seguinte estratégia de solução de problemas.
- Determine se as equações de velocidade, energia ou período são válidas para o problema em questão. Caso contrário, comece com os primeiros princípios que usamos para derivar essas equações.
- Para começar com os primeiros princípios, desenhe um diagrama de corpo livre e aplique a lei da gravitação de Newton e a segunda lei de Newton.
- Junto com as definições de velocidade e energia, aplique a segunda lei do movimento de Newton aos corpos de interesse.
Determine a velocidade orbital e o período da Estação Espacial Internacional (ISS).
Estratégia
Como a ISS orbita 4,00 x 10 2 km acima da superfície da Terra, o raio no qual ela orbita é R E + 4,00 x 10 2 km. Usamos as Equações\ ref {13.7} e\ ref {13.8} para determinar a velocidade e o período orbitais, respectivamente.
Solução
Usando a Equação\ ref {13.7}, a velocidade orbital é
\[v_{orbit} = \sqrt{\frac{GM_{E}}{r}} = \sqrt{\frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}{(6.36 \times 10^{6} + 4.00 \times 10^{5})\; m}} = 7.67 \times 10^{3}\; m/s\]
que é cerca de 17.000 mph. Usando a Equação\ ref {13.8}, o período é
\[T = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} = 2 \pi \sqrt{\frac{(6.36 \times 10^{6} + 4.00 \times 10^{5}\; m)^{3}}{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}} = 5.55 \times 10^{3}\; s\]
o que é pouco mais de 90 minutos.
Significância
A ISS é considerada em órbita terrestre baixa (LEO). Quase todos os satélites estão em LEO, incluindo a maioria dos satélites meteorológicos. Os satélites GPS, com cerca de 20.000 km, são considerados órbita média da Terra. Quanto mais alta a órbita, mais energia é necessária para colocá-la lá e mais energia é necessária para alcançá-la para reparos. De particular interesse são os satélites em órbita geossíncrona. Todas as antenas parabólicas fixas no chão apontando para o céu, como antenas de recepção de TV, são apontadas para satélites geossíncronos. Esses satélites são colocados à distância exata e logo acima do equador, de forma que seu período de órbita seja de 1 dia. Eles permanecem em uma posição fixa em relação à superfície da Terra.
Por qual fator o raio deve mudar para reduzir a velocidade orbital de um satélite pela metade? Por qual fator isso mudaria o período?
Determine a massa da Terra a partir da órbita da Lua.
Estratégia
Usamos a Equação\ ref {13.8}, resolvemos por M E e substituímos o período e o raio da órbita. O raio e o período da órbita da Lua foram medidos com precisão razoável há milhares de anos. A partir dos dados astronômicos no Apêndice D, o período da Lua é de 27,3 dias = 2,36 x 10 6 s, e a distância média entre os centros da Terra e a Lua é de 384.000 km.
Solução
Resolvendo para\(M_E\),
\[\begin{split} T & = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} \\ M_{E} & = \frac{2 \pi^{2} r^{3}}{GT^{2}} = \frac{4 \pi^{2} (3.84 \times 10^{8}\; m)^{3}}{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(2.36 \times 10^{6}\; s)^{2}} = 6.01 \times 10^{24}\; kg \ldotp \end{split}\]
Significância
Compare isso com o valor de 5,96 x 10 24 kg que obtivemos no Exemplo 13.3.3, usando o valor de\(g\) na superfície da Terra. Embora esses valores sejam muito próximos (~ 0,8%), ambos os cálculos usam valores médios. O valor de g varia do equador aos pólos em aproximadamente 0,5%. Mas a Lua tem uma órbita elíptica na qual o valor de r varia pouco mais de 10%. (O tamanho aparente da Lua cheia, na verdade, varia aproximadamente nessa quantidade, mas é difícil perceber por meio de observação casual, pois o tempo de um extremo ao outro é de muitos meses.)
Há outra consideração sobre esse último cálculo de M E. Derivamos a Equação\ ref {13.8} assumindo que o satélite orbita ao redor do centro do corpo astronômico no mesmo raio usado na expressão da força gravitacional entre eles. Que suposição é feita para justificar isso? A Terra é cerca de 81 vezes mais massiva que a Lua. A Lua orbita em torno do centro exato da Terra?
Vamos revisitar o Exemplo 13.2.2. Suponha que as galáxias Via Láctea e Andrômeda estejam em uma órbita circular uma sobre a outra. Qual seria a velocidade de cada um e qual seria seu período orbital? Suponha que a massa de cada uma seja de 800 bilhões de massas solares e seus centros estejam separados por 2,5 milhões de anos-luz.
Estratégia
Não podemos usar as equações\ ref {13.7} e\ ref {13.8} diretamente porque elas foram derivadas assumindo que o objeto de massa m orbitava em torno do centro de um planeta muito maior de massa M. Determinamos a força gravitacional no Exemplo 13.2.2 usando a lei da gravitação universal de Newton. Podemos usar a segunda lei de Newton, aplicada à aceleração centrípeta de qualquer galáxia, para determinar sua velocidade tangencial. A partir desse resultado, podemos determinar o período da órbita.
Solução
No Exemplo 13.2.2, descobrimos que a força entre as galáxias é
\[F_{12} = G \frac{m_{1} m_{2}}{r^{2}} = (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})\frac{[(800 \times 10^{9})(2.0 \times 10^{30})\; kg]^{2}}{[(2.5 \times 10^{6})(9.5 \times 10^{15})\; m]^{2}} = 3.0 \times 10^{29}\; N\]
e que a aceleração de cada galáxia é
\[a = \frac{F}{m} = \frac{3.0 \times 10^{29}\; N}{(800 \times 10^{9})(2.0 \times 10^{30})\; kg} = 1.9 \times 10^{-13}\; m/s^{2} \ldotp\]
Como as galáxias estão em uma órbita circular, elas têm aceleração centrípeta. Se ignorarmos o efeito de outras galáxias, então, como aprendemos em Momento Linear e Colisões e Rotação de Eixo Fixo, os centros de massa das duas galáxias permanecem fixos. Portanto, as galáxias devem orbitar em torno desse centro de massa comum. Para massas iguais, o centro de massa está exatamente a meio caminho entre elas. Portanto, o raio da órbita, órbita r, não é o mesmo que a distância entre as galáxias, mas metade desse valor, ou 1,25 milhão de anos-luz. Esses dois valores diferentes são mostrados na Figura\(\PageIndex{3}\).

Usando a expressão para aceleração centrípeta, temos
\[\begin{split} a_{c} & = \frac{v_{orbit}^{2}}{r_{orbit}} \\ 1.9 \times 10^{-13}\; m/s^{2} & = \frac{v_{orbit}^{2}}{(1.25 \times 10^{6})(9.5 \times 10^{15})\; m} \ldotp \end{split}\]
Resolvendo a velocidade da órbita, temos\(v_{orbit} = 47\, km/s\). Finalmente, podemos determinar o período da órbita diretamente de
\[T = \frac{2 \pi r}{v_{orbit}}\]
para descobrir que o período é T = 1,6 x 10 18 s, cerca de 50 bilhões de anos.
Significância
A velocidade orbital de 47 km/s pode parecer alta à primeira vista. Mas essa velocidade é comparável à velocidade de escape do Sol, que calculamos em um exemplo anterior. Para dar ainda mais perspectiva, esse período é quase quatro vezes maior do que o tempo em que o Universo existe.
Na verdade, o movimento relativo atual dessas duas galáxias é tal que se espera que elas colidam em cerca de 4 bilhões de anos. Embora a densidade das estrelas em cada galáxia torne improvável uma colisão direta de quaisquer duas estrelas, essa colisão terá um efeito dramático na forma das galáxias. Exemplos de tais colisões são bem conhecidos em astronomia.
As galáxias não são objetos únicos. Como a força gravitacional de uma galáxia exercida sobre as estrelas “mais próximas” da outra galáxia se compara às mais distantes? Que efeito isso teria na forma das próprias galáxias?
Consulte a página do Sloan Digital Sky Survey para obter mais informações sobre galáxias em colisão.
Use essa simulação interativa para mover o Sol, a Terra, a Lua e a estação espacial para ver os efeitos em suas forças gravitacionais e caminhos orbitais. Visualize os tamanhos e as distâncias entre diferentes corpos celestes e desligue a gravidade para ver o que aconteceria sem ela.
Energia em órbitas circulares
Em Energia Potencial Gravitacional e Energia Total, argumentamos que os objetos são ligados gravitacionalmente se sua energia total for negativa. O argumento foi baseado no caso simples em que a velocidade estava diretamente longe ou em direção ao planeta. Agora examinamos a energia total de uma órbita circular e mostramos que, de fato, a energia total é negativa. Como fizemos anteriormente, começamos com a segunda lei de Newton aplicada a uma órbita circular,
\[\begin{split} \frac{GmM_{E}}{r^{2}} & = ma_{c} = \frac{mv^{2}}{r} \\ \frac{GmM_{E}}{r} & = mv^{2} \ldotp \end{split}\]
Na última etapa, multiplicamos por\(r\) em cada lado. O lado direito é apenas o dobro da energia cinética, então temos
\[K = \frac{1}{2} mv^{2} = \frac{GmM_{E}}{2r} \ldotp\]
A energia total é a soma das energias cinética e potencial, então nosso resultado final é
\[E = K + U = \frac{GmM_{E}}{2r} - \frac{GmM_{E}}{r} = - \frac{GmM_{E}}{2r} \ldotp \label{13.9}\]
Podemos ver que a energia total é negativa, com a mesma magnitude da energia cinética. Para órbitas circulares, a magnitude da energia cinética é exatamente metade da magnitude da energia potencial. Surpreendentemente, esse resultado se aplica a quaisquer duas massas em órbitas circulares em torno de seu centro de massa comum, a uma distância r uma da outra. A prova disso é deixada como um exercício. Veremos na próxima seção que uma expressão muito semelhante se aplica ao caso de órbitas elípticas.
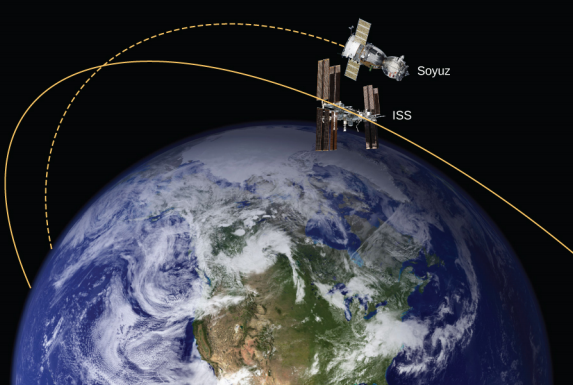
No Exemplo 13.4.1, calculamos a energia necessária para simplesmente levantar o veículo Soyuz de 9000 kg da superfície da Terra até a altura da ISS, 400 km acima da superfície. Em outras palavras, encontramos sua mudança na energia potencial. Agora perguntamos: qual mudança total de energia no veículo Soyuz é necessária para tirá-lo da superfície da Terra e colocá-lo em órbita com a ISS para um encontro (Figura\(\PageIndex{4}\))? Quanto dessa energia total é energia cinética?
Estratégia
A energia necessária é a diferença entre a energia total da Soyuz em órbita e a energia na superfície da Terra. Podemos usar a Equação\ ref {13.9} para encontrar a energia total da Soyuz na órbita da ISS. Mas a energia total na superfície é simplesmente a energia potencial, pois parte do repouso. [Note que não usamos a Equação\ ref {13.9} na superfície, pois não estamos em órbita na superfície.] A energia cinética pode então ser encontrada a partir da diferença na mudança total de energia e na mudança na energia potencial encontrada no Exemplo 13.4.1. Alternativamente, podemos usar a Equação\ ref {13.7} para encontrar a órbita v e calcular a energia cinética diretamente dela. A energia total necessária é então a energia cinética mais a mudança na energia potencial encontrada no Exemplo 13.4.1.
Solução
Da Equação\ ref {13.9}, a energia total da Soyuz na mesma órbita da ISS é
\[\begin{split} E_{orbit} & = K_{orbit} + U_{orbit} = - \frac{GmM_{E}}{2r} \\ & = \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(9000\; kg)(5.96 \times 10^{24}\; kg)}{2(6.36 \times 10^{6} + 4.00 \times 10^{5}\; m)} = -2.65 \times 10^{11}\; J \ldotp \end{split}\]
A energia total na superfície da Terra é
\[\begin{split} E_{surface} & = K_{surface} + U_{surface} = 0 - \frac{GmM_{E}}{r} \\ & = - \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(9000\; kg)(5.96 \times 10^{24}\; kg)}{(6.36 \times 10^{6}\; m)} \\ & = -5.63 \times 10^{11}\; J \ldotp \end{split}\]
A mudança na energia é
\[\Delta E = E_{orbit}− E_{surface} = 2.98 x 10^{11}\, J. \nonumber\]
Para obter a energia cinética, subtraímos a mudança na energia potencial do Exemplo 13.4.1,\(\Delta\) U = 3,32 x 10 10 J. Isso nos dá a órbita K = (2,98 x 10 11) − (3,32 x 10 10) = 2,65 x 10 11 J. Como dito anteriormente, a energia cinética de uma órbita circular é sempre metade da magnitude da energia potencial e o mesmo que a magnitude da energia total. Nosso resultado confirma isso.
A segunda abordagem é usar a Equação\ ref {13.7} para encontrar a velocidade orbital da Soyuz, o que fizemos para a ISS em Example\(\PageIndex{1}\).
\[ \begin{align*} v_{orbit} &= \sqrt{\frac{GM_{E}}{r}} \\[4pt]&= \sqrt{\frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}{(6.36 \times 10^{6} + 4.00 \times 10^{5})\; m}} \\[4pt] &= 7.67 \times 10^{3}\; m/s \end{align*}\]
Portanto, a energia cinética da Soyuz em órbita é
\[ \begin{align*}K_{orbit} &= \frac{1}{2} mv_{orbit}^{2} \\[4pt]&= \frac{1}{2} (9000\; kg)(7.67 \times 10^{3}\; m/s)^{2} \\[4pt]&= 2.65 \times 10^{11}\; J,\end{align*}\]
o mesmo que no método anterior. A energia total é apenas
\[ \begin{align*}E_{orbit} &= K_{orbit} + \Delta U \\[4pt]&= (2.65 \times 10^{11}) + (3.32 \times 10^{10}) \\[4pt]&= 2.95 \times 10^{11}\; J \ldotp\end{align*}\]
Significância
A energia cinética da Soyuz é quase oito vezes a mudança em sua energia potencial, ou 90% da energia total necessária para o encontro com a ISS. E é importante lembrar que essa energia representa apenas a energia que deve ser dada à Soyuz. Com nossa tecnologia atual de foguetes, a massa do sistema de propulsão (o combustível do foguete, seu contêiner e sistema de combustão) excede em muito a da carga útil, e uma quantidade enorme de energia cinética deve ser dada a essa massa. Portanto, o custo real da energia é muitas vezes o da mudança na energia da própria carga útil.


