13.4: Energia potencial gravitacional e energia total
- Page ID
- 184884
- Determine mudanças na energia potencial gravitacional em grandes distâncias
- Aplique a conservação de energia para determinar a velocidade de escape
- Determine se os corpos astronômicos estão ligados gravitacionalmente
Estudamos a energia potencial gravitacional em Energia Potencial e Conservação de Energia, onde o valor de\(g\) permaneceu constante. Agora desenvolvemos uma expressão que funciona em distâncias de forma que g não seja constante. Isso é necessário para calcular corretamente a energia necessária para colocar satélites em órbita ou enviá-los em missões no espaço.
Energia potencial gravitacional além da Terra
Definimos trabalho e energia potencial, anteriormente. A utilidade dessas definições é a facilidade com que podemos resolver muitos problemas usando a conservação de energia. A energia potencial é particularmente útil para forças que mudam com a posição, assim como a força gravitacional ocorre em grandes distâncias. Em Energia Potencial e Conservação de Energia, mostramos que a mudança na energia potencial gravitacional próxima à superfície da Terra é
\[ \Delta U = mg(y_2− y_1) \label{simple}\]
Isso funciona muito bem se\(g\) não mudar significativamente entre y 1 e y 2. Retornamos à definição de trabalho e energia potencial para derivar uma expressão correta em distâncias maiores. Lembre-se de que o trabalho (W) é a integral do produto escalar entre força e distância. Essencialmente, é o produto do componente de uma força ao longo de um deslocamento vezes esse deslocamento. Definimos\(\Delta u\) como o negativo do trabalho realizado pela força que associamos à energia potencial. Para maior clareza, derivamos uma expressão para mover uma massa m da distância r 1 do centro da Terra para a distância r 2. No entanto, o resultado pode ser facilmente generalizado para quaisquer dois objetos, alterando sua separação de um valor para outro.
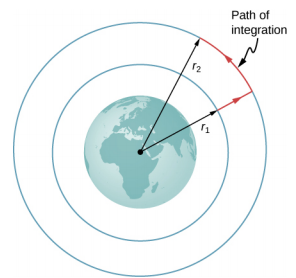
Considere a Figura\(\PageIndex{1}\), na qual tomamos m de uma distância r 1 do centro da Terra para uma distância que é r 2 do centro. A gravidade é uma força conservadora (sua magnitude e direção são apenas funções de localização), então podemos seguir qualquer caminho que desejarmos, e o resultado para o cálculo do trabalho é o mesmo. Seguimos o caminho mostrado, pois isso simplifica muito a integração. Primeiro, nos movemos radialmente para fora da distância r 1 para a distância r 2 e depois nos movemos ao longo do arco de um círculo até chegarmos à posição final. Durante a porção radial,\(\vec{F}\) é oposta à direção que viajamos ao longo de d\(\vec{r}\), então
\[E = K_1 + U_1 = K_2 + U_2\]
Ao longo do arco,\(\vec{F}\) é perpendicular a d\(\vec{r}\), então\(\vec{F}\; \cdotp d \vec{r}\) = 0. Nenhum trabalho é feito à medida que nos movemos ao longo do arco. Usando a expressão para a força gravitacional e observando os valores\(\vec{F}\; \cdotp d \vec{r}\) ao longo dos dois segmentos de nosso caminho, temos
\[ \begin{align} \Delta U &= - \int_{r_{1}}^{r_{2}} \vec{F}\; \cdotp d \vec{r} \\[4pt] &= GM_{E} m \int_{r_{1}}^{r_{2}} \frac{dr}{r^{2}} \\[4pt] &= GM_{E} m \left(\dfrac{1}{r_{1}} - \dfrac{1}{r_{2}}\right) \ldotp \label{eq13.3} \end{align} \]
Já que\(\Delta U = U_2 − U_1\) podemos adotar uma expressão simples para\(U\):
\[U = - \frac{GM_{E} m}{r} \ldotp \label{13.4}\]
Observe dois itens importantes com essa definição. Primeiro,\(U → 0\) como\(r → \infty\). A energia potencial é zero quando as duas massas estão infinitamente distantes. Somente a diferença\(U\) é importante, então a escolha de\(U = 0\) for\(r = \infty\) é meramente conveniente. (Lembre-se de que, em problemas de gravidade anteriores, você era livre para pegar\(U = 0\) na parte superior ou inferior de um prédio ou em qualquer lugar.) Em segundo lugar, observe que isso\(U\) se torna cada vez mais negativo à medida que as massas se aproximam. Isso é consistente com o que você aprendeu sobre energia potencial em energia potencial e conservação de energia. À medida que as duas massas são separadas, um trabalho positivo deve ser feito contra a força da gravidade e, portanto,\(U\) aumenta (se torna menos negativo). Todas as massas naturalmente se unem sob a influência da gravidade, caindo de uma energia potencial maior para uma menor.
Quanta energia é necessária para levantar o veículo Soyuz de 9000 kg da superfície da Terra até a altura da ISS, 400 km acima da superfície?
Estratégia
Use a Equação\ ref {eq13.3} para encontrar a mudança na energia potencial da carga útil. Essa quantidade de trabalho ou energia deve ser fornecida para levantar a carga útil.
Solução
Prestando atenção ao fato de começarmos na superfície da Terra e terminarmos a 400 km acima da superfície, a mudança\(U\) é
Nós inserimos os valores
- \(m = 9000\; kg\)
- \(M_{E} = 5.96 \times 10^{24}\; kg\)
- \(R_{E} = 6.37 \times 10^{6}\; m\)
e converta 400 km em 4,00 x 10 5 m. Encontramos\(\Delta U = 3.32 \times 10^{10} J\). É positivo, indicando um aumento na energia potencial, como seria de esperar.
Significância
Para fins de perspectiva, considere que o uso médio de energia doméstica nos EUA em 2013 foi de 909 kWh por mês. Isso é energia de
\[909\; kWh \times 1000\; W/kW \times 3600\; s/h = 3.27 \times 10^{9}\; J\; per\; month \ldotp \nonumber\]
Portanto, nosso resultado é um gasto de energia equivalente a 10 meses. No entanto, essa é apenas a energia necessária para elevar a carga útil em 400 km. Se quisermos que a Soyuz fique em órbita para que ela possa se encontrar com a ISS e não apenas cair de volta à Terra, ela precisa de muita energia cinética. Como vemos na próxima seção, essa energia cinética é cerca de cinco vezes a de\(\Delta\) U. Além disso, muito mais energia é gasta elevando o próprio sistema de propulsão. Viajar no espaço não é barato.
Por que não usar a expressão mais simples em Equation\ ref {simple} em vez disso? Quão significativo seria o erro? (O valor\(g\) a 400 km acima da Terra é 8,67 m/s 2.)
Conservação de energia
Em Energia Potencial e Conservação de Energia, descrevemos como aplicar a conservação de energia para sistemas com forças conservadoras. Conseguimos resolver muitos problemas, especialmente aqueles que envolvem a gravidade, usando de forma mais simples a conservação de energia. Esses princípios e estratégias de resolução de problemas se aplicam igualmente bem aqui. A única mudança é colocar a nova expressão de energia potencial na equação de conservação de energia,
\[E_{tot} = K_1 + U_1 = K_2 + U_2.\]
\[\frac{1}{2} mv_{1}^{2} - \frac{GMm}{r_{1}} = \frac{1}{2} mv_{2}^{2} - \frac{GMm}{r_{2}} \label{13.5}\]
Observe que usamos M, em vez de M E, como um lembrete de que não estamos restritos a problemas envolvendo a Terra. No entanto, ainda assumimos que m << M. (Para problemas em que isso não é verdade, precisamos incluir a energia cinética de ambas as massas e usar a conservação do momento para relacionar as velocidades entre si. Mas o princípio continua o mesmo.)
Velocidade de escape
A velocidade de escape geralmente é definida como a velocidade inicial mínima de um objeto que é necessária para escapar da superfície de um planeta (ou de qualquer corpo grande como uma lua) e nunca mais retornar. Como de costume, presumimos que não há perda de energia em uma atmosfera, caso haja alguma.
Considere o caso em que um objeto é lançado da superfície de um planeta com uma velocidade inicial direcionada para longe do planeta. Com a velocidade mínima necessária para escapar, o objeto simplesmente ficaria infinitamente distante, ou seja, o objeto cede a última de sua energia cinética assim que atinge o infinito, onde a força da gravidade se torna zero. Como U → 0 como r →\(\infty\), isso significa que a energia total é zero. Assim, encontramos a velocidade de escape da superfície de um corpo astronômico de massa M e raio R definindo a energia total igual a zero. Na superfície do corpo, o objeto está localizado\(r_1 = R\) e tem velocidade de escape\(v_1 = v_{esc}\). Ele alcança\(r_2 = \infty\) com velocidade\(v_2 = 0\). Substituindo na Equação\ ref {13.5}, temos
\[\frac{1}{2} mv_{esc}^{2} - \frac{GMm}{R} = \frac{1}{2} m0^{2} - \frac{GMm}{\infty} = 0 \ldotp\]
Resolvendo a velocidade de escape,
\[v_{esc} = \sqrt{\frac{2GM}{R}} \ldotp \label{13.6}\]
Observe que\(m\) foi cancelado fora da equação. A velocidade de escape é a mesma para todos os objetos, independentemente da massa. Além disso, não estamos restritos à superfície do planeta; R pode ser qualquer ponto de partida além da superfície do planeta.
Qual é a velocidade de fuga da superfície da Terra? Suponha que não haja perda de energia devido à resistência do ar. Compare isso com a velocidade de escape do Sol, começando na órbita da Terra.
Estratégia
Usamos a Equação 13.6, definindo claramente os valores de R e M. Para escapar da Terra, precisamos da massa e do raio da Terra. Para escapar do Sol, precisamos da massa do Sol e da distância orbital entre a Terra e o Sol.
Solução
Substituindo os valores da massa e do raio da Terra diretamente na Equação 13.6, obtemos
\[ \begin {align*} v_{esc} &= \sqrt{\frac{2GM}{R}} \\[4pt] &= \sqrt{\frac{2 (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}{6.37 \times 10^{6}\; m}} \\[4pt] &= 1.12 \times 10^{4}\; m/s \ldotp \end{align*}\]
Isso é cerca de 11 km/s ou 25.000 mph. Para escapar do Sol, partindo da órbita da Terra, usamos R = R ES = 1,50 x 10 11 m e M Sol = 1,99 x 10 30 kg. O resultado é v esc = 4,21 x 10 4 m/s ou cerca de 42 km/s.
Significância
A velocidade necessária para escapar do Sol (sair do sistema solar) é quase quatro vezes a velocidade de escape da superfície da Terra. Mas há ajuda nos dois casos. A Terra está girando, a uma velocidade de quase 1,7 km/s no equador, e podemos usar essa velocidade para ajudar a escapar ou alcançar a órbita. Por esse motivo, muitas empresas espaciais comerciais mantêm instalações de lançamento próximas ao equador. Para escapar do Sol, há ainda mais ajuda. A Terra gira em torno do Sol a uma velocidade de aproximadamente 30 km/s. Ao se lançar na direção em que a Terra está se movendo, precisamos de apenas 12 km/s adicionais. O uso da assistência gravitacional de outros planetas, essencialmente uma técnica de estilingue gravitacional, permite que as sondas espaciais alcancem velocidades ainda maiores. Nessa técnica de estilingue, o veículo se aproxima do planeta e é acelerado pela atração gravitacional do planeta. Ele tem sua maior velocidade no ponto de aproximação mais próximo, embora desacelere na mesma medida à medida que se afasta. Mas em relação ao planeta, a velocidade do veículo muito antes da aproximação, e muito depois, é a mesma. Se as direções forem escolhidas corretamente, isso pode resultar em um aumento significativo (ou diminuição, se necessário) na velocidade do veículo em relação ao resto do sistema solar.
Energia e objetos gravitacionalmente ligados
Conforme mencionado anteriormente, a velocidade de escape pode ser definida como a velocidade inicial de um objeto que pode escapar da superfície de uma lua ou planeta. De forma mais geral, é a velocidade em qualquer posição em que a energia total seja zero. Se a energia total for zero ou maior, o objeto escapa. Se a energia total for negativa, o objeto não poderá escapar. Vamos ver por que esse é o caso.
Conforme observado anteriormente, vemos isso\(U → 0\) como\(r → \infty\). Se a energia total for zero, então, quando m atinge um valor de r que se aproxima do infinito, U se torna zero, assim como a energia cinética. Assim, m fica infinitamente longe de M. Ele “acabou de escapar” M. Se a energia total for positiva, então a energia cinética permanece em\(r = \infty\) e certamente m não retorna. Quando a energia total é zero ou maior, dizemos que m não está gravitacionalmente ligado a M.
Por outro lado, se a energia total for negativa, a energia cinética deve chegar a zero em algum valor finito de r, onde U é negativo e igual à energia total. O objeto nunca pode ultrapassar essa distância finita de M, pois para isso seria necessário que a energia cinética se tornasse negativa, o que não é possível. Dizemos que m está gravitacionalmente ligado a M.
Simplificamos essa discussão assumindo que o objeto estava se afastando diretamente do planeta. O que é notável é que o resultado se aplica a qualquer velocidade. A energia é uma grandeza escalar e, portanto, a Equação\ ref {13.5} é uma equação escalar — a direção da velocidade não desempenha nenhum papel na conservação da energia. É possível ter um sistema gravitacionalmente ligado em que as massas não “caiam juntas”, mas mantenham um movimento orbital umas sobre as outras.
Temos uma observação final importante. Anteriormente, afirmamos que se a energia total for zero ou maior, o objeto escapa. Estritamente falando, a Equação\ ref {13.5} e a Equação\ ref {13.6} se aplicam a objetos pontuais. Eles também se aplicam a objetos de tamanho finito, esfericamente simétricos, desde que o valor\(r\) na Equação\ ref {13.5} seja sempre maior do que a soma dos raios dos dois objetos. Se r se tornar menor que essa soma, os objetos colidem. (Mesmo para valores maiores de r, mas perto da soma dos raios, as forças gravitacionais das marés podem criar efeitos significativos se ambos os objetos forem do tamanho de um planeta. Examinamos os efeitos das marés em Tidal Forces.) Nem a energia total positiva nem a negativa impedem a colisão de massas de tamanho finito. Para objetos reais, a direção é importante.
Vamos considerar novamente o exemplo anterior, onde calculamos a velocidade de escape da Terra e do Sol, começando pela órbita da Terra. Observamos que a Terra já tem uma velocidade orbital de 30 km/s. Como vemos na próxima seção, essa é a velocidade tangencial necessária para permanecer em órbita circular. Se um objeto tivesse essa velocidade à distância da órbita da Terra, mas estivesse se afastando diretamente do Sol, até onde ele viajaria antes de descansar? Ignore os efeitos gravitacionais de qualquer outro corpo.
Estratégia
O objeto tem energias cinéticas e potenciais iniciais que podemos calcular. Quando sua velocidade chega a zero, está na distância máxima do Sol. Usamos a Equação 13.5, conservação de energia, para encontrar a distância na qual a energia cinética é zero.
Solução
A posição inicial do objeto é o raio de órbita da Terra e a velocidade inicial é dada como 30 km/s. A velocidade final é zero, então podemos resolver a distância nesse ponto a partir da equação de conservação de energia. Usando R ES = 1,50 x 10 11 m e M Sun = 1,99 x 10 30 kg, temos
\[\begin{split} \frac{1}{2} mv_{1}^{2} - \frac{GMm}{r_{1}} & = \frac{1}{2} mv_{2}^{2} - \frac{GMm}{r_{2}} \\ \frac{1}{2} \cancel{m} (30\; km/s)^{2} - \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(1.99 \times 10^{30}\; kg) \cancel{m}}{1.50 \times 10^{11}\; m} & = \frac{1}{2} m(0)^{2} - \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(1.99 \times 10^{30}\; kg) \cancel{m}}{r_{2}} \end{split}\]
onde a massa m é cancelada. Resolvendo para r 2, obtemos r 2 = 3,0 x 10 11 m. Observe que isso é o dobro da distância inicial do Sol e nos leva além da órbita de Marte, mas não exatamente até o cinturão de asteróides.
Significância
O objeto nesse caso atingiu uma distância exatamente o dobro da distância orbital inicial. Veremos o motivo disso na próxima seção, quando calcularmos a velocidade das órbitas circulares.
Suponha que você esteja em uma espaçonave em órbita ao redor do Sol na órbita da Terra, mas longe da Terra (para que ela possa ser ignorada). Como você poderia redirecionar sua velocidade tangencial para a direção radial de forma que você pudesse então passar pela órbita de Marte? O que seria necessário para mudar apenas a direção da velocidade?


