13.3: Gravitação perto da superfície da Terra
- Page ID
- 184911
- Explique a conexão entre as constantes G e g
- Determine a massa de um corpo astronômico a partir da aceleração em queda livre em sua superfície
- Descreva como o valor de g varia de acordo com a localização e a rotação da Terra
Nesta seção, observamos como a lei da gravitação de Newton se aplica à superfície de um planeta e como ela se conecta com o que aprendemos anteriormente sobre queda livre. Também examinamos os efeitos gravitacionais nos corpos esféricos.
Peso
Lembre-se de que a aceleração de um objeto em queda livre perto da superfície da Terra é de aproximadamente g = 9,80 m/s 2. A força que causa essa aceleração é chamada de peso do objeto e, pela segunda lei de Newton, tem o valor mg. Esse peso está presente independentemente de o objeto estar em queda livre. Agora sabemos que essa força é a força gravitacional entre o objeto e a Terra. Se substituirmos mg pela magnitude de\(\vec{F}_{12}\) na lei da gravitação universal de Newton, m por m 1 e M E por m 2, obtemos a equação escalar
\[mg = G \frac{m M_{E}}{r^{2}} \label{13.1}\]
onde r é a distância entre os centros de massa do objeto e a Terra. O raio médio da Terra é de cerca de 6370 km. Portanto, para objetos dentro de alguns quilômetros da superfície da Terra, podemos pegar\(r = R_E\) (Figura\(\PageIndex{1}\)). A massa m do objeto é cancelada, deixando
\[g = G \frac{M_{E}}{r^{2}} \ldotp \label{13.2}\]
Isso explica por que todas as massas caem livremente com a mesma aceleração. Ignoramos o fato de que a Terra também acelera em direção ao objeto que cai, mas isso é aceitável desde que a massa da Terra seja muito maior do que a do objeto.
Você já se perguntou como conhecemos a massa da Terra? Certamente não podemos colocá-lo em uma balança. Os valores de g e o raio da Terra foram medidos com precisão razoável séculos atrás.
- Use os valores padrão de g, R E e Equação\ ref {13.2} para encontrar a massa da Terra.
- Estime o valor de g na Lua. Use o fato de que a Lua tem um raio de cerca de 1700 km (um valor dessa precisão foi determinado há muitos séculos) e suponha que ela tenha a mesma densidade média da Terra, 5500 kg/m 3.
Estratégia
Com os valores conhecidos de g e R E, podemos usar a Equação\ ref {13.2} para encontrar M E. Para a Lua, usamos a suposição de densidade média igual para determinar a massa a partir de uma proporção dos volumes da Terra e da Lua.
Solução
- Reorganizando a equação\ ref {13.2}, temos $$M_ {E} =\ frac {g R_ {E} ^ {2}} {G} =\ frac {(9,80\; m/s^ {2}) (6,37\ times 10^ {6}\; m) ^ {2}} {6,67\ times 10^ {-11}\; N\;\ cdotp m^ {2} /kg^ {2}} = 5,95\ times 10^ {24}\; kg\ ldotp$$
- O volume de uma esfera é proporcional ao raio cúbico, então uma razão simples nos dá $$\ frac {M_ {M}} {M_ {E}} =\ frac {R_ {M} ^ {3}} {R_ {E} ^ {3}}\ rightarrow M_ {M} =\ left (\ dfrac {(1.7\ times 10^ {6}\ m;) ^ {3}} {(6,37\ times 10^ {6}\; m) ^ {3}}\ right) (5,95\ times 10^ {24}\; kg) = 1,1\ times 10^ {23}\; kg\ LDOTP$$Agora usamos Equação\ ref {13.2}. $$g_ {M} = G\ frac {M_ {M}} {r_ {M} ^ {2}} = (6,67\ times 10^ {-11}\; N\;\ cdotp m^ {2} /kg^ {2})\ left (\ dfrac {1,1\ times 10^ {23}\; kg} {(1,7\ times 10^ {6}; m) ^ {2}}\ direita) = 2,5\; m/s^ {2} $$
Significância
Assim que Cavendish determinou o valor de G em 1798, a massa da Terra pôde ser calculada. (Na verdade, esse foi o propósito final do experimento de Cavendish em primeiro lugar.) O valor que calculamos para g da Lua está incorreto. A densidade média da Lua é, na verdade, de apenas 3340 kg/m 3 e g = 1,6 m/s 2 na superfície. Newton tentou medir a massa da Lua comparando o efeito do Sol nas marés oceânicas da Terra com o da Lua. Seu valor era um fator de dois muito pequeno. Os valores mais precisos para g e a massa da Lua vêm do rastreamento do movimento de naves espaciais que orbitaram a Lua. Mas a massa da Lua pode, na verdade, ser determinada com precisão sem ir à Lua. A Terra e a Lua orbitam em torno de um centro de massa comum, e medições astronômicas cuidadosas podem determinar essa localização. A razão entre a massa da Lua e a da Terra é a razão entre [a distância do centro de massa comum ao centro da Lua] e [a distância do centro de massa comum ao centro da Terra].
Mais adiante nesta seção, veremos que a massa de outros corpos astronômicos também pode ser determinada pelo período de pequenos satélites que os orbitam. Mas até Cavendish determinar o valor de G, as massas de todos esses corpos eram desconhecidas.
Qual é o valor de g 400 km acima da superfície da Terra, onde a Estação Espacial Internacional está em órbita?
Solução
Usando o valor de M E e observando que o raio é r = R E + 400 km, usamos a Equação\ ref {13.2} para encontrar g. Da Equação\ ref {13.2} temos
\[g = G \frac{M_{E}}{r^{2}} = (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2}) \left(\dfrac{5.96 \times 10^{24}\; kg}{(6.37 \times 10^{6} + 400 \times 10^{3}\; m)^{2}}\right) = 8.67\; m/s^{2} \ldotp\]
Significância
Muitas vezes vemos vídeos de astronautas em estações espaciais, aparentemente sem peso. Mas, claramente, a força da gravidade está agindo sobre eles. Comparando o valor de g que acabamos de calcular com o da Terra (9,80 m/s 2), vemos que os astronautas da Estação Espacial Internacional ainda têm 88% de seu peso. Eles só parecem estar sem peso porque estão em queda livre. Voltaremos a isso em Satellite Orbits and Energy.
Como seu peso no topo de um prédio alto se compara ao do primeiro andar? Você acha que os engenheiros precisam levar em consideração a mudança no valor de g ao projetar o suporte estrutural para um edifício muito alto?
O campo gravitacional
A equação\ ref {13.2} é uma equação escalar, fornecendo a magnitude da aceleração gravitacional em função da distância do centro da massa que causa a aceleração. Mas poderíamos ter mantido a forma vetorial da força da gravidade na Equação\ ref {13.1} e escrito a aceleração na forma vetorial como
\[\vec{g} = G \frac{M}{r^{2}} \hat{r} \ldotp\]
Identificamos o campo vetorial representado por\(\vec{g}\) como o campo gravitacional causado pela massa M. Podemos imaginar o campo conforme mostrado na Figura\(\PageIndex{2}\). As linhas são direcionadas radialmente para dentro e distribuídas simetricamente em torno da massa.
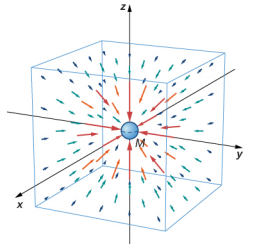
Como acontece com qualquer campo vetorial, a direção de\(\vec{g}\) é paralela às linhas do campo em qualquer ponto. A intensidade de\(\vec{g}\) em qualquer ponto é inversamente proporcional ao espaçamento entre linhas. Outra forma de afirmar isso é que a magnitude do campo em qualquer região é proporcional ao número de linhas que passam por uma unidade de área de superfície, efetivamente uma densidade de linhas. Como as linhas estão igualmente espaçadas em todas as direções, o número de linhas por unidade de área de superfície a uma distância r da massa é o número total de linhas dividido pela área da superfície de uma esfera de raio r, que é proporcional a r 2. Portanto, essa imagem representa perfeitamente a lei do inverso do quadrado, além de indicar a direção do campo. Na imagem de campo, dizemos que uma massa m interage com o campo gravitacional de massa M. Usaremos o conceito de campos com grande vantagem nas seções posteriores sobre eletromagnetismo.
Peso aparente: contabilizando a rotação da Terra
Como vimos em Aplicações das Leis de Newton, objetos que se movem em velocidade constante em um círculo têm uma aceleração centrípeta direcionada para o centro do círculo, o que significa que deve haver uma força líquida direcionada para o centro desse círculo. Como todos os objetos na superfície da Terra se movem através de um círculo a cada 24 horas, deve haver uma força centrípeta líquida em cada objeto direcionada para o centro desse círculo.
Vamos primeiro considerar um objeto de massa m localizado no equador, suspenso em uma escala (Figura\(\PageIndex{3}\)). A balança exerce uma força ascendente\(\vec{F}_{s}\) longe do centro da Terra. Essa é a leitura da balança e, portanto, é o peso aparente do objeto. O peso (mg) aponta para o centro da Terra. Se a Terra não estivesse girando, a aceleração seria zero e, consequentemente, a força líquida seria zero, resultando em F s = mg. Essa seria a leitura verdadeira do peso.
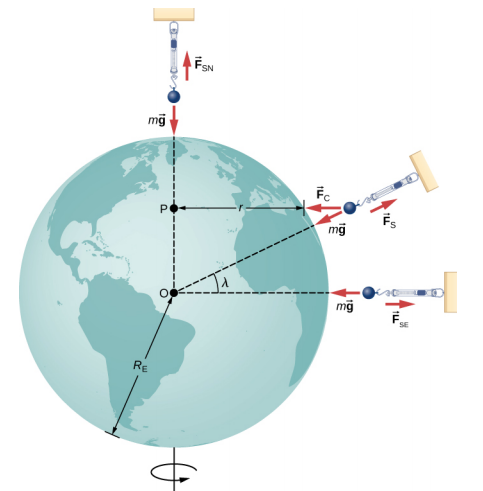
Com a rotação, a soma dessas forças deve fornecer a aceleração centrípeta,\(a_c\). Usando a segunda lei de Newton, temos
\[\sum F = F_{s} - mg = ma_{c} \quad where\; a_{c} = - \frac{v^{2}}{r} \ldotp \label{13.3}\]
Observe que a c aponta na mesma direção do peso; portanto, é negativo. A velocidade tangencial v é a velocidade no equador e r é R E. Podemos calcular a velocidade simplesmente observando que objetos no equador percorrem a circunferência da Terra em 24 horas. Em vez disso, vamos usar a expressão alternativa para a c de Movimento em duas e três dimensões. Lembre-se de que a velocidade tangencial está relacionada à velocidade angular (\(\omega\)) por v =\(\omega\) r. Portanto, temos um c = −r\(\omega\) 2. Ao reorganizar a Equação 13.3 e substituir r = R E, o peso aparente no equador é
\[F_{s} = m (g - R_{E} \omega^{2}) \ldotp\]
A velocidade angular da Terra em todos os lugares é
\[\omega = \frac{2 \pi\; rad}{24\; hr \times 3600\; s/hr} = 7.27 \times 10^{-5}\; rad/s \ldotp\]
Substituindo os valores de R E e\(\omega\), temos R E\(\omega\) 2 = 0,0337 m/s 2. Isso é apenas 0,34% do valor da gravidade, então é claramente uma pequena correção.
Com que rapidez a Terra precisaria girar para que aqueles no equador tivessem peso aparente zero? Qual seria a duração do dia?
Estratégia
Usando a Equação\ ref {13.3}, podemos definir o peso aparente (F s) como zero e determinar a aceleração centrípeta necessária. A partir disso, podemos encontrar a velocidade no equador. A duração do dia é o tempo necessário para uma rotação completa.
Solução
Da Equação\ ref {13.2}, temos\(\sum\) F = F s − mg = ma c, então definindo F s = 0, obtemos g = a c. Usando a expressão para a c, substituindo o raio da Terra e o valor padrão da gravidade, obtemos
\[\begin{split} a_{c} & = \frac{v^{2}}{r} = g \\ v & = \sqrt{gr} = \sqrt{(9.80\; m/s^{2})(6.37 \times 10^{6}\; m)} = 7.91 \times 10^{3}\; m/s \ldotp \end{split}\]
O período T é o tempo para uma rotação completa. Portanto, a velocidade tangencial é a circunferência dividida por T, então temos
\[\begin{split} v & = \frac{2 \pi r}{T} \\ T & = \frac{2 \pi r}{v} = \frac{2 \pi (6.37 \times 10^{6}\; m)}{7.91 \times 10^{3}\; m/s} = 5.06 \times 10^{3}\; s \ldotp \end{split}\]
Isso é cerca de 84 minutos.
Significância
Veremos mais adiante nesta seção que essa velocidade e duração do dia também seriam a velocidade orbital e o período de um satélite em órbita na superfície da Terra. Embora tal órbita não seja possível perto da superfície da Terra devido à resistência do ar, certamente é possível apenas algumas centenas de quilômetros acima da Terra.
Resultados Fora do Equador
Nos pólos, a c → 0 e Fs = mg, assim como é o caso sem rotação. Em qualquer outra latitude\(\lambda\), a situação é mais complicada. A aceleração centrípeta é direcionada para o ponto P na figura, e o raio se torna\(r = R_E \cos \lambda\). A soma vetorial do peso e\(\vec{F}_{s}\) deve apontar para o ponto P, portanto,\(\vec{F}_{s}\) não aponta mais para longe do centro da Terra. (A diferença é pequena e exagerada na figura.) Um prumo sempre apontará nessa direção desviada. Todos os edifícios são construídos alinhados ao longo dessa direção desviada, não ao longo de um raio que passa pelo centro da Terra. Para os edifícios mais altos, isso representa um desvio de alguns metros no topo.
Também é importante notar que a Terra não é uma esfera perfeita. O interior é parcialmente líquido, e isso aumenta a protuberância da Terra no equador devido à sua rotação. O raio da Terra é cerca de 30 km maior no equador em comparação com os pólos. Resta como um exercício comparar a força da gravidade nos pólos com a do equador usando a Equação\ ref {13.2}. A diferença é comparável à diferença devido à rotação e está na mesma direção. Aparentemente, você realmente pode perder “peso” se mudando para os trópicos.
Gravidade longe da superfície
Anteriormente, declaramos sem provas que a lei da gravitação se aplica a objetos esfericamente simétricos, onde a massa de cada corpo age como se estivesse no centro do corpo. Como a Equação\ ref {13.2} é derivada da Equação\ ref {13.1}, ela também é válida para distribuições de massa simétricas, mas ambas as equações são válidas somente para valores de\(r ≥ R_E\). Como vimos no Exemplo 13.4, a 400 km acima da superfície da Terra, onde orbita a Estação Espacial Internacional, o valor de\(g\) é 8,67 m/s 2. (Veremos mais tarde que essa também é a aceleração centrípeta da ISS.)
Para\(r < R_E\), a Equação\ ref {13.1} e a Equação\ ref {13.2} não são válidas. No entanto, podemos determinar g para esses casos usando um princípio que vem da lei de Gauss, que é uma ferramenta matemática poderosa que estudamos com mais detalhes posteriormente no curso. Uma consequência da lei de Gauss, aplicada à gravitação, é que somente a massa dentro de r contribui para a força gravitacional. Além disso, essa massa, assim como antes, pode ser considerada localizada no centro. O efeito gravitacional da massa fora de r tem efeito líquido zero.
Dois casos especiais muito interessantes ocorrem. Para um planeta esférico com densidade constante, a massa dentro de r é a densidade vezes o volume dentro de r. Essa massa pode ser considerada localizada no centro. Substituindo M E apenas pela massa dentro de r, M =\(\rho\) x (volume de uma esfera) e R E por r, a Equação\ ref {13.2} se torna
\[g = G \frac{M_{E}}{R_{E}^{2}} = G \frac{\rho \left(\dfrac{4}{3} \pi r^{3}\right)}{r^{2}} = \frac{4}{3} G \rho \pi r \ldotp\]
O valor de g e, portanto, seu peso, diminui linearmente à medida que você desce por um buraco até o centro do planeta esférico. No centro, você está sem peso, pois a massa do planeta puxa igualmente em todas as direções. Na verdade, a densidade da Terra não é constante, nem a Terra é sólida por toda parte. A figura\(\PageIndex{4}\) mostra o perfil de\(g\) se a Terra tivesse densidade constante e o perfil mais provável com base em estimativas de densidade derivadas de dados sísmicos.
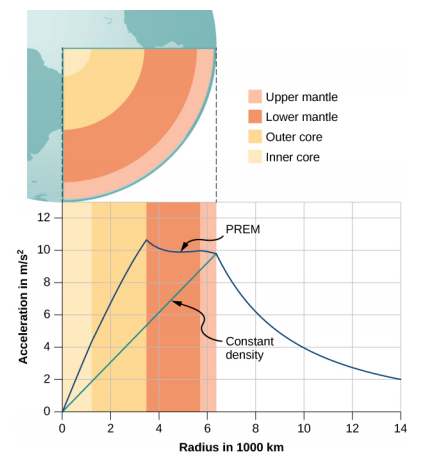
O segundo caso interessante diz respeito a viver em um planeta de concha esférico. Esse cenário foi proposto em muitas histórias de ficção científica. Ignorando problemas significativos de engenharia, a concha pode ser construída com o raio e a massa total desejados, de forma que g na superfície seja igual ao da Terra. Você consegue adivinhar o que acontece quando você desce em um elevador até o interior da concha, onde não há massa entre você e o centro? Que benefícios isso proporcionaria ao viajar grandes distâncias de um ponto da esfera para outro? E, finalmente, que efeito haveria se o planeta estivesse girando?


