12.5: Tensão, deformação e módulo de elasticidade (Parte 2)

Tensão em massa, deformação e módulo

Ao mergulhar na água, você sente uma força pressionando cada parte do corpo de todas as direções. O que você está experimentando então é estresse em massa ou, em outras palavras, pressão. A tensão em massa sempre tende a diminuir o volume envolto pela superfície de um objeto submerso. As forças dessa “compressão” são sempre perpendiculares à superfície submersa Figura\(\PageIndex{1}\). O efeito dessas forças é diminuir o volume do objeto submerso em uma quantidade\(\Delta\) V em comparação com o volume V ₀ do objeto na ausência de tensão em massa. Esse tipo de deformação é chamado de deformação em massa e é descrito por uma mudança no volume em relação ao volume original:

\[bulk\; strain = \frac{\Delta V}{V_{0}} \label{12.37}\]

Figura\(\PageIndex{1}\): Um objeto sob crescente tensão de volume sempre sofre uma diminuição em seu volume. Forças iguais perpendiculares à superfície atuam de todas as direções. O efeito dessas forças é diminuir o volume na quantidade\(\Delta\) V em comparação com o volume original, V ₀.

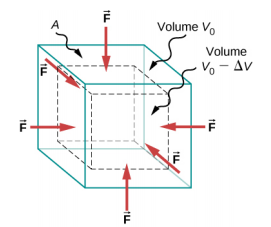
A deformação total resulta da tensão total, que é uma força F _\(\perp\)normal para uma superfície que pressiona a área de superfície unitária A de um objeto submerso. Esse tipo de quantidade física, ou pressão p, é definido como

\[pressure = p \equiv \frac{F_{\perp}}{A} \ldotp \label{12.38}\]

Estudaremos a pressão nos fluidos com mais detalhes em Mecânica dos Fluidos. Uma característica importante da pressão é que ela é uma grandeza escalar e não tem nenhuma direção específica; ou seja, a pressão age igualmente em todas as direções possíveis. Ao mergulhar a mão na água, você sente a mesma pressão atuando na superfície superior da mão e na superfície inferior, na superfície lateral ou na superfície da pele entre os dedos. O que você está percebendo neste caso é um aumento na pressão\(\Delta\) p sobre o que você está acostumado a sentir quando sua mão não está submersa na água. O que você sente quando sua mão não está submersa na água é a pressão normal p ₀ de uma atmosfera, que serve como ponto de referência. A tensão total é esse aumento na pressão, ou\(\Delta\) p, acima do nível normal, p ₀.

Quando a tensão total aumenta, a deformação a granel aumenta em resposta, de acordo com a Equação 12.4.4. A constante de proporcionalidade nessa relação é chamada de módulo de massa, B ou

\[B = \frac{bulk\; stress}{bulk\; strain} = \frac{\Delta p}{\frac{\Delta V}{V_{0}}} = - \Delta p \frac{V_{0}}{\Delta V} \ldotp \label{12.39}\]

O sinal de menos que aparece na Equação\ ref {12.39} é para consistência, para garantir que\(B\) seja uma quantidade positiva. Observe que o sinal de menos (—) é necessário porque um aumento\(\Delta\) p na pressão (uma quantidade positiva) sempre causa uma diminuição\(\Delta\) V no volume, e a diminuição no volume é uma quantidade negativa. O recíproco do módulo de massa é chamado de compressibilidade k, ou

\[k = \frac{1}{B} = - \frac{\frac{\Delta V}{V_{0}}}{\Delta p} \ldotp \label{12.40}\]

O termo “compressibilidade” é usado em relação aos fluidos (gases e líquidos). A compressibilidade descreve a mudança no volume de um fluido por unidade de aumento na pressão. Os fluidos caracterizados por uma grande compressibilidade são relativamente fáceis de comprimir. Por exemplo, a compressibilidade da água é 4,64 x 10 ⁻⁵ /atm e a compressibilidade da acetona é 1,45 x 10 ⁻⁴ /atm. Isso significa que, sob um aumento de pressão de 1,0 atm, a diminuição relativa no volume é aproximadamente três vezes maior para a acetona do que para a água.

Exemplo\(\PageIndex{1}\): Hydraulic Press

Em uma prensa hidráulica Figura\(\PageIndex{2}\), um volume de óleo de 250 litros está sujeito a um aumento de pressão de 2300 psi. Se a compressibilidade do óleo for 2,0 x 10 ⁻⁵/atm, encontre a deformação total e a diminuição absoluta no volume de óleo quando a prensa estiver em operação.

Figura\(\PageIndex{2}\): Em uma prensa hidráulica, quando um pequeno pistão é deslocado para baixo, a pressão no óleo é transmitida por todo o óleo até o pistão grande, fazendo com que o pistão grande se mova para cima. Uma pequena força aplicada a um pistão pequeno causa uma grande força de prensagem, que o pistão grande exerce sobre um objeto que é levantado ou comprimido. O dispositivo funciona como uma alavanca mecânica.

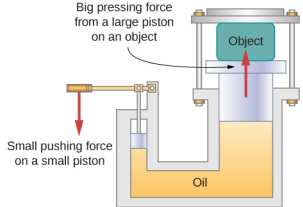
Estratégia

Devemos inverter a Equação\ ref {12.40} para encontrar a cepa em massa. Primeiro, convertemos o aumento de pressão de psi para atm,\(\Delta\) p = 2300 psi =\(\frac{2300}{14.7\; atm}\) ≈ 160 atm e identificamos V ₀ = 250 L.

Solução

Substituindo valores na equação, temos

\[bulk\; strain = \frac{\Delta V}{V_{0}} = \frac{\Delta p}{B} = k \Delta p = (2.0 \times 10^{-5}\; /atm)(160\; atm) = 0.0032\]

resposta

\[\Delta V = 0.0032 V_{0} = 0.0032 (250\; L) = 0.78\; L \ldotp\]

Significância

Observe que, como a compressibilidade da água é 2,32 vezes maior que a do óleo, se a substância de trabalho na prensa hidráulica desse problema fosse alterada para água, a deformação total e a mudança de volume seriam 2,32 vezes maiores.

Exercício\(\PageIndex{1}\)

Se a força normal atuando em cada face de uma peça cúbica de aço de 1,0 m ³ for alterada em 1,0 x 10 ⁷ N, encontre a mudança resultante no volume da peça de aço.

Tensão de cisalhamento, deformação e módulo

Os conceitos de tensão de cisalhamento e deformação dizem respeito apenas a objetos ou materiais sólidos. Edifícios e placas tectônicas são exemplos de objetos que podem estar sujeitos a tensões de cisalhamento. Em geral, esses conceitos não se aplicam aos fluidos.

A deformação por cisalhamento ocorre quando duas forças antiparalelas de igual magnitude são aplicadas tangencialmente a superfícies opostas de um objeto sólido, não causando nenhuma deformação na direção transversal à linha de força, como no exemplo típico de tensão de cisalhamento ilustrado na Figura\(\PageIndex{3}\). A deformação por cisalhamento é caracterizada por um deslocamento gradual\(\Delta\) x das camadas na direção tangente às forças atuantes. Essa gradação em\(\Delta\) x ocorre na direção transversal ao longo de alguma distância L ₀. A deformação de cisalhamento é definida pela razão entre o maior deslocamento\(\Delta\) x e a distância transversal L ₀

\[shear\; strain = \frac{\Delta x}{L_{0}} \ldotp \label{12.41}\]

A deformação por cisalhamento é causada pela tensão de cisalhamento. A tensão de cisalhamento é devida a forças que atuam paralelamente à superfície. Usamos o símbolo F _{\(\parallel\)}para essas forças. A magnitude F _{\(\parallel\)}por área de superfície A onde a força de cisalhamento é aplicada é a medida da tensão de cisalhamento

\[shear\; stress = \frac{F_{\parallel}}{A} \ldotp \label{12.42}\]

O módulo de cisalhamento é a constante de proporcionalidade na Equação\ ref {12.33} e é definido pela razão entre tensão e deformação. O módulo de cisalhamento é comumente indicado por\(S\):

\[S = \frac{shear\; stress}{shear\; strain} = \frac{\frac{F_{\parallel}}{A}}{\frac{\Delta x}{L_{0}}} = \frac{F_{\parallel}}{A} \frac{L_{0}}{\Delta x} \ldotp \label{12.43}\]

Figura\(\PageIndex{3}\): Um objeto sob tensão de cisalhamento: Duas forças antiparalelas de igual magnitude são aplicadas tangencialmente a superfícies paralelas opostas do objeto. O contorno da linha tracejada mostra a deformação resultante. Não há mudança na direção transversal às forças atuantes e o comprimento transversal L ₀ não é afetado. A deformação por cisalhamento é caracterizada por um deslocamento gradual\(\Delta\) x das camadas na direção tangente às forças.

Exemplo\(\PageIndex{2}\): An Old Bookshelf

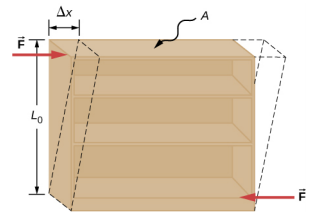
Um faxineiro tenta mover uma estante velha e pesada em um piso acarpetado empurrando tangencialmente a superfície da prateleira superior. No entanto, o único efeito perceptível desse esforço é semelhante ao visto na Figura\(\PageIndex{2}\), e ele desaparece quando a pessoa para de empurrar. A estante tem 180,0 cm de altura e 90,0 cm de largura com quatro prateleiras de 30,0 cm de profundidade, todas parcialmente carregadas com livros. O peso total da estante e dos livros é de 600,0 N. Se a pessoa pressionar 50,0 N na prateleira superior, deslocando a prateleira superior horizontalmente em 15,0 cm em relação à prateleira inferior imóvel, encontre o módulo de cisalhamento da estante.

Estratégia

As únicas informações relevantes são as dimensões físicas da estante, o valor da força tangencial e o deslocamento que essa força causa. Identificamos F _{\(\parallel\)}= 50,0 N,\(\Delta\) x = 15,0 cm, L ₀ = 180,0 cm e A = (30,0 cm) (90,0 cm) = 2700,0 cm ² e usamos a Equação\ ref {12.43} para calcular o módulo de cisalhamento.

Solução

Substituindo números nas equações, obtemos o módulo de cisalhamento

\[S = \frac{F_{\parallel}}{A} \frac{L_{0}}{\Delta x} = \frac{50.0\; N}{2700.0\; cm^{2}} \frac{180.0\; cm}{15.0\; cm} = \frac{2}{9} \frac{M}{cm^{2}} = \frac{2}{9} \times 10^{4}\; N/m^{2} = \frac{20}{9} \times 10^{3}\; Pa = 2.222\; kPa \ldotp \nonumber\]

Também podemos encontrar tensão de cisalhamento e deformação, respectivamente:

\[\frac{F_{\parallel}}{A} = \frac{50.0\; N}{2700.0\; cm^{2}} = \frac{5}{27}\; kPa = 185.2\; Pa \nonumber\]

\[\frac{\Delta x}{L_{0}} = \frac{15.0\; cm}{180.0\; cm} = \frac{1}{12} = 0.083 \ldotp \nonumber\]

Significância

Se a pessoa neste exemplo desse um empurrão saudável na prateleira, pode acontecer que o cisalhamento induzido a derrube em uma pilha de lixo. Quase o mesmo mecanismo de cisalhamento é responsável por falhas em barragens e diques cheios de terra; e, em geral, por deslizamentos de terra.

Exercício\(\PageIndex{2}\)

Explique por que os conceitos de módulo de Young e módulo de cisalhamento não se aplicam aos fluidos.