12.4: Tensão, deformação e módulo de elasticidade (Parte 1)

Objetivos de

• Explicar os conceitos de tensão e deformação na descrição de deformações elásticas de materiais
• Descreva os tipos de deformação elástica de objetos e materiais

Um modelo de corpo rígido é um exemplo idealizado de um objeto que não se deforma sob as ações de forças externas. É muito útil ao analisar sistemas mecânicos — e muitos objetos físicos são, de fato, rígidos em grande medida. A extensão em que um objeto pode ser percebido como rígido depende das propriedades físicas do material do qual ele é feito. Por exemplo, uma bola de pingue-pongue feita de plástico é quebradiça e uma bola de tênis feita de borracha é elástica quando acionada por forças de compressão. No entanto, em outras circunstâncias, tanto uma bola de pingue-pongue quanto uma bola de tênis podem quicar bem como corpos rígidos. Da mesma forma, alguém que projeta membros protéticos pode ser capaz de aproximar a mecânica dos membros humanos modelando-os como corpos rígidos; no entanto, a combinação real de ossos e tecidos é um meio elástico.

No restante desta seção, passamos da consideração de forças que afetam o movimento de um objeto para aquelas que afetam a forma de um objeto. Uma mudança na forma devido à aplicação de uma força é conhecida como deformação. Sabe-se que mesmo forças muito pequenas causam alguma deformação. A deformação é experimentada por objetos ou meios físicos sob a ação de forças externas — por exemplo, isso pode ser esmagar, apertar, rasgar, torcer, cortar ou separar os objetos. Na linguagem da física, dois termos descrevem as forças em objetos sob deformação: tensão e deformação.

A tensão é uma quantidade que descreve a magnitude das forças que causam a deformação. A tensão é geralmente definida como força por unidade de área. Quando as forças puxam um objeto e causam seu alongamento, como o alongamento de um elástico, chamamos essa tensão de tensão de tração. Quando as forças causam a compressão de um objeto, chamamos isso de tensão compressiva. Quando um objeto está sendo espremido por todos os lados, como um submarino nas profundezas de um oceano, chamamos esse tipo de estresse de estresse em massa (ou estresse de volume). Em outras situações, as forças atuantes podem não ser nem de tração nem de compressão e ainda produzir uma deformação perceptível. Por exemplo, suponha que você segure um livro firmemente entre as palmas das mãos, depois, com uma mão, pressione e puxe a capa frontal para longe de você, enquanto com a outra mão você pressiona e puxa a contracapa em sua direção. Nesse caso, quando as forças de deformação agem tangencialmente à superfície do objeto, nós as chamamos de forças de “cisalhamento” e a tensão que elas causam é chamada de tensão de cisalhamento.

A unidade de estresse do SI é o pascal (Pa). Quando um newton de força pressiona uma área de superfície unitária de um metro quadrado, a tensão resultante é um pascal:

\[one\; pascal = 1.0\; Pa = \frac{1.0\; N}{1.0\; m^{2}} \ldotp\]

No sistema britânico de unidades, a unidade de estresse é 'psi', que significa 'libra por polegada quadrada' (lb/in ²). Outra unidade que é frequentemente usada para estresse em massa é o atm (atmosfera). Os fatores de conversão são

\[1\; psi = 6895\; Pa\; and\; 1\; Pa = 1.450 \times 10^{-4}\; psi\]

\[1\; atm = 1.013 \times 10^{5}\; Pa = 14.7\; psi \ldotp\]

Um objeto ou meio sob estresse fica deformado. A quantidade que descreve essa deformação é chamada de deformação. A deformação é dada como uma mudança fracionária no comprimento (sob tensão de tração) ou no volume (sob tensão total) ou na geometria (sob tensão de cisalhamento). Portanto, a deformação é um número adimensional. A deformação sob uma tensão de tração é chamada de deformação de tração, a deformação sob tensão total é chamada de deformação em massa (ou deformação de volume) e a causada pela tensão de cisalhamento é chamada de deformação de cisalhamento.

Quanto maior a tensão, maior a deformação; no entanto, a relação entre deformação e tensão não precisa ser linear. Somente quando a tensão é suficientemente baixa é a deformação que ela causa em proporção direta ao valor da tensão. A constante de proporcionalidade nessa relação é chamada de módulo elástico. No limite linear de baixos valores de tensão, a relação geral entre tensão e deformação é

\[stress = (elastic\; modulus) \times strain \ldotp \label{12.33}\]

Como podemos ver na análise dimensional dessa relação, o módulo de elasticidade tem a mesma unidade física da tensão porque a deformação é adimensional.

Também podemos ver na Equação\ ref {12.33} que quando um objeto é caracterizado por um grande valor de módulo de elasticidade, o efeito da tensão é pequeno. Por outro lado, um pequeno módulo de elasticidade significa que a tensão produz grande deformação e deformação perceptível. Por exemplo, uma tensão em um elástico produz maior deformação (deformação) do que a mesma tensão em uma faixa de aço das mesmas dimensões porque o módulo de elasticidade da borracha é duas ordens de magnitude menor do que o módulo de elasticidade do aço.

O módulo elástico para tensão de tração é chamado de módulo de Young; o módulo de tensão em massa é chamado de módulo de massa; e o módulo de cisalhamento é chamado de módulo de cisalhamento. Observe que a relação entre tensão e deformação é uma relação observada, medida em laboratório. Os módulos elásticos para vários materiais são medidos sob várias condições físicas, como temperatura variável, e coletados em tabelas de dados de engenharia para referência (Tabela\(\PageIndex{1}\)). Essas tabelas são referências valiosas para a indústria e para qualquer pessoa envolvida em engenharia ou construção. Na próxima seção, discutiremos as relações entre deformação e tensão além do limite linear representado pela Equação\ ref {12.33}, em toda a faixa de valores de tensão até um ponto de fratura. No restante desta seção, estudamos o limite linear expresso pela Equação\ ref {12.33}.

Tabela\(\PageIndex{1}\): Módulos elásticos aproximados para materiais selecionados

Material	Módulo de Young × 10 ^10 Pa	Módulo de granel × 10 ^10 Pa	Módulo de cisalhamento × 10 ^10 Pa
Alumínio	7.0	7.5	2,5
Osso (tensão)	1.6	0,8	8.0
Osso (compressão)	0,9
Latão	9.0	6.0	3.5
Tijolo	1,5
Concreto	2.0
Cobre	11.0	14,0	4.4
Copo de vidro	6.0	5,0	2,5
Granito	4.5	4.5	2.0
Cabelo (humano)	1,0
Madeira dura	1,5		1,0
Ferro	21,0	16,0	7.7
Liderar	1.6	4.1	0,6
Mármore	6.0	7.0	2.0
Níquel	21,0	17,0	7.8
Poliestireno	3,0
Seda	6.0
Fio de aranha	3,0
Aço	20,0	16,0	7.5
Acetona		0,07
Etanol		0,09
Glicerina		0,45
Mercúrio		2,5
Água		0,22

Tensão de tração ou compressão, deformação e módulo de Young

A tensão ou compressão ocorre quando duas forças antiparalelas de igual magnitude atuam sobre um objeto ao longo de apenas uma de suas dimensões, de forma que o objeto não se mova. Uma maneira de visualizar essa situação é ilustrada na Figura\(\PageIndex{1}\). Um segmento de haste é esticado ou comprimido por um par de forças atuando ao longo de seu comprimento e perpendicularmente à sua seção transversal. O efeito líquido de tais forças é que a haste muda seu comprimento do comprimento original L ₀ que tinha antes do aparecimento das forças, para um novo comprimento L que ela tem sob a ação das forças. Essa mudança no comprimento\(\Delta\) L = L − L ₀ pode ser alongamento (quando\(L\) é maior que o comprimento original\(L_o\)) ou contração (quando L é menor que o comprimento original L ₀). A tensão de tração e a deformação ocorrem quando as forças estão esticando um objeto, causando seu alongamento, e a mudança de comprimento\(\Delta L\) é positiva. A tensão compressiva e a deformação ocorrem quando as forças contraem um objeto, causando seu encurtamento, e a mudança de comprimento\(\Delta L\) é negativa.

Em qualquer uma dessas situações, definimos tensão como a razão entre a força de deformação e\(F_{\perp}\) a área da seção transversal A do objeto que está sendo deformado. O símbolo F _\(\perp\)que reservamos para a força de deformação significa que essa força atua perpendicularmente à seção transversal do objeto. Forças que atuam paralelamente à seção transversal não alteram o comprimento de um objeto. A definição da tensão de tração é

\[tensile\; stress = \frac{F_{\perp}}{A} \ldotp \label{12.34}\]

A deformação de tração é a medida da deformação de um objeto sob tensão de tração e é definida como a mudança fracionária do comprimento do objeto quando o objeto sofre tensão de tração

\[tensile\; strain = \frac{\Delta L}{L_{0}} \ldotp \label{12.35}\]

A tensão compressiva e a deformação são definidas pelas mesmas fórmulas, Equações\ ref {12.34} e\ ref {12.35}, respectivamente. A única diferença da situação de tração é que, para tensão de compressão e deformação, tomamos valores absolutos dos lados direitos na Equação\ ref {12.34} e\ ref {12.35}.

Figura\(\PageIndex{1}\): Quando um objeto está em tensão ou compressão, a força total sobre ele é zero, mas o objeto se deforma alterando seu comprimento original L ₀. (a) Tensão: A haste é alongada por\(\Delta\) L. (b) Compressão: A haste é contraída por\(\Delta\) L. Em ambos os casos, a força de deformação atua ao longo do comprimento da haste e perpendicularmente à sua seção transversal. Na faixa linear de baixa tensão, a área da seção transversal da haste não muda.

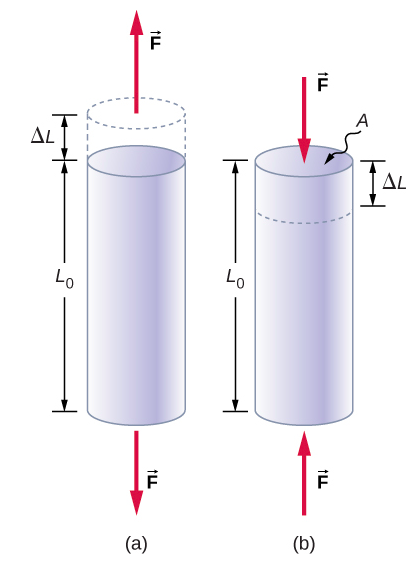
O módulo de Young\(Y\) é o módulo de elasticidade quando a deformação é causada por tensão de tração ou compressão e é definido pela Equação\ ref {12.33}. Dividindo essa equação pela deformação de tração, obtemos a expressão para o módulo de Young:

\[Y = \frac{tensile\; stress}{tensile\; strain} = \frac{\frac{F_{\perp}}{A}}{\frac{\Delta L}{L_{0}}} = \frac{F_{\perp}}{A} = \frac{L_{0}}{\Delta L} \ldotp \label{12.36}\]

Exemplo\(\PageIndex{1}\): Compressive Stress in a Pillar

Uma escultura pesando 10.000 N repousa sobre uma superfície horizontal no topo de um pilar vertical de 6,0 m de altura\(\PageIndex{1}\). Figura. A área da seção transversal do pilar é de 0,20 m ² e é feita de granito com uma densidade de massa de 2700 kg/m ³. Encontre a tensão de compressão na seção transversal localizada a 3,0 m abaixo da parte superior do pilar e o valor da deformação compressiva do segmento superior de 3,0 m do pilar.

Figura\(\PageIndex{2}\): Coluna de Nelson em Trafalgar Square, Londres, Inglaterra. (crédito: modificação da obra de Cristian Bortes)

Estratégia

Primeiro, encontramos o peso da seção superior de 3,0 m de comprimento do pilar. A força normal que atua na seção transversal localizada a 3,0 m abaixo do topo é a soma do peso do pilar e do peso da escultura. Uma vez que temos a força normal, usamos a Equação 12.34 para encontrar a tensão. Para encontrar a deformação compressiva, encontramos o valor do módulo de Young para granito na Tabela\(\PageIndex{1}\) e na Equação invertida\ ref {12.36}.

Solução

O volume do segmento do pilar com altura h = 3,0 m e área da seção transversal A = 0,20 m ² é

\[V = Ah = (0.20\; m^{2})(3.0\; m) = 0.60\; m^{3} \ldotp\]

Com a densidade do granito\(\rho\) = 2,7 x 10 ³ kg/m ³, a massa do segmento do pilar é

\[m = \rho V = (2.7 \times 10^{3}\; kg/m^{3})(0.60\; m^{3}) = 1.60 \times 10^{3}\; kg \ldotp\]

O peso do segmento do pilar é

\[w_{p} = mg = (1.60 \times 10^{3}\; kg)(9.80\; m/s^{2}) = 1.568 \times 10^{4}\; N \ldotp\]

O peso da escultura é w _s = 1,0 x 10 ⁴ N, então a força normal na superfície da seção transversal localizada 3,0 m abaixo da escultura é

\[F_{\perp} = w_{p} + w_{s} = (1.568 + 1.0) \times 10^{4}\; N = 2.568 \times 10^{4}\; N \ldotp\]

Portanto, o estresse é

\[stress = \frac{F_{\perp}}{A} = \frac{2.568 \times 10^{4}\; N}{0.20 m^{2}} = 1.284 \times 10^{5}\; Pa = 128.4\; kPa \ldotp\]

O módulo de Young para granito é Y = 4,5 x 10 ¹⁰ Pa = 4,5 x 10 ⁷ kPa. Portanto, a tensão compressiva nessa posição é

\[strain = \frac{stress}{Y} = \frac{128.4\; kPa}{4.5 \times 10^{7}\; kPa} = 2.85 \times 10^{-6} \ldotp\]

Significância

Observe que a força normal atuando na área da seção transversal do pilar não é constante ao longo de seu comprimento, mas varia de seu menor valor na parte superior até seu maior valor na parte inferior do pilar. Assim, se o pilar tiver uma área de seção transversal uniforme ao longo de seu comprimento, a tensão é maior em sua base.

Exercício\(\PageIndex{2}\)

Encontre a tensão compressiva e a deformação na base da coluna de Nelson.

Exemplo\(\PageIndex{2}\): Stretching a Rod

Uma haste de aço de 2,0 m de comprimento tem uma área de seção transversal de 0,30 cm ². A haste faz parte de um suporte vertical que sustenta uma plataforma pesada de 550 kg que fica presa à extremidade inferior da haste. Ignorando o peso da haste, qual é a tensão de tração na haste e o alongamento da haste sob a tensão?

Estratégia

Primeiro, calculamos a tensão de tração na haste sob o peso da plataforma de acordo com a Equação 12.34. Em seguida, invertemos a Equação 12.36 para encontrar o alongamento da haste, usando L ₀ = 2,0 m. Na Tabela 12.1, o módulo de Young para o aço é Y = 2,0 x 10 ¹¹ Pa.

Solução

Substituir valores numéricos nas equações nos dá

\[\begin{split} \frac{F_{\perp}}{A} & = \frac{(550\; kg)(9.8\; m/s^{2})}{3.0 \times 10^{-5}\; m^{2}} = 1.8 \times 10^{8}\; Pa \\ \Delta L & = \frac{F_{\perp}}{A} \frac{L_{0}}{Y} = (1.8 \times 10^{8}\; Pa) \left(\dfrac{2.0\; m}{2.0 \times 10^{11}\; Pa}\right) = 1.8 \times 10^{-3}\; m = 1.8\; mm \ldotp \end{split}\]

Significância

Da mesma forma que no exemplo com a coluna, a tensão de tração neste exemplo não é uniforme ao longo do comprimento da haste. Ao contrário do exemplo anterior, no entanto, se o peso da haste for levado em consideração, a tensão na haste será maior na parte superior e menor na parte inferior da haste onde o equipamento está conectado.

Exercício\(\PageIndex{2}\)

Um fio de 2,0 m de comprimento se estende por 1,0 mm quando submetido a uma carga. Qual é a tensão de tração no fio?

Os objetos geralmente podem sofrer tensão compressiva e tensão de tração simultaneamente\(\PageIndex{3}\). Figura. Um exemplo é uma prateleira longa carregada de livros pesados que fica entre os suportes das extremidades sob o peso dos livros. A superfície superior da prateleira está em tensão de compressão e a superfície inferior da prateleira está em tensão de tração. Da mesma forma, feixes longos e pesados cedem sob seu próprio peso. Na construção moderna de edifícios, essas deformações de flexão podem ser quase eliminadas com o uso da Figura I-beams\(\PageIndex{4}\).

Figura\(\PageIndex{3}\): (a) Um objeto dobrado para baixo sofre tensão de tração (alongamento) na seção superior e tensão compressiva (compressão) na seção inferior. (b) Os levantadores de peso de elite costumam dobrar barras de ferro temporariamente durante o levantamento, como na competição das Olimpíadas de 2012. (crédito b: modificação da obra de Oleksandr Kocherzhenko)

Figura\(\PageIndex{4}\): Vigas em I de aço são usadas na construção para reduzir as deformações de flexão. (crédito: modificação do trabalho do “Distrito Europeu do Corpo de Engenheiros do Exército dos EUA” /Flickr)

Simulação

Uma caixa pesada repousa sobre uma mesa sustentada por três colunas. Veja esta demonstração para mover a caixa e ver como a compressão (ou tensão) nas colunas é afetada quando a caixa muda de posição.