12.3: Exemplos de equilíbrio estático

Objetivos de

• Identifique e analise situações de equilíbrio estático
• Configure um diagrama de corpo livre para um objeto estendido em equilíbrio estático
• Configure e resolva condições de equilíbrio estático para objetos em equilíbrio em várias situações físicas

Todos os exemplos deste capítulo são problemas planares. Consequentemente, usamos condições de equilíbrio na forma de componente da Equação 12.2.9 à Equação 12.2.11. Introduzimos uma estratégia de resolução de problemas no Exemplo 12.1 para ilustrar o significado físico das condições de equilíbrio. Agora, generalizamos essa estratégia em uma lista de etapas a serem seguidas ao resolver problemas de equilíbrio estático para corpos rígidos estendidos. Prosseguimos em cinco etapas práticas.

Estratégia de resolução de problemas: equilíbrio estático

1. Identifique o objeto a ser analisado. Para alguns sistemas em equilíbrio, pode ser necessário considerar mais de um objeto. Identifique todas as forças que atuam no objeto. Identifique as perguntas que você precisa responder. Identifique as informações fornecidas no problema. Em problemas realistas, algumas informações importantes podem estar implícitas na situação em vez de serem fornecidas explicitamente.
2. Configure um diagrama de corpo livre para o objeto. (a) Escolha o quadro de referência xy para o problema. Desenhe um diagrama de corpo livre para o objeto, incluindo somente as forças que atuam sobre ele. Quando adequado, represente as forças em termos de seus componentes no quadro de referência escolhido. Ao fazer isso para cada força, risque a força original para não incluir erroneamente a mesma força duas vezes nas equações. Rotule todas as forças — você precisará disso para calcular corretamente as forças líquidas nas direções x e y. Para uma força desconhecida, a direção deve ser atribuída arbitrariamente; pense nela como uma “direção de trabalho” ou “direção suspeita”. A direção correta é determinada pelo sinal que você obtém na solução final. Um sinal de mais (+) significa que a direção de trabalho é a direção real. Um sinal de menos (−) significa que a direção real é oposta à direção de trabalho assumida. (b) Escolha a localização do eixo de rotação; em outras palavras, escolha o ponto de articulação em relação ao qual você calculará os torques das forças atuantes. No diagrama de corpo livre, indique a localização do pivô e dos braços de alavanca das forças atuantes — você precisará disso para calcular corretamente os torques. Na seleção do pivô, lembre-se de que o pivô pode ser colocado em qualquer lugar que você desejar, mas o princípio orientador é que a melhor escolha simplificará ao máximo o cálculo do torque líquido ao longo do eixo de rotação.
3. Configure as equações de equilíbrio para o objeto. (a) Use o diagrama de corpo livre para escrever uma condição de equilíbrio correta Equação 12.2.9 para componentes de força na direção x. (b) Use o diagrama de corpo livre para escrever uma condição de equilíbrio correta Equação 12.2.13 para componentes de força na direção y. (c) Use o diagrama de corpo livre para escrever uma condição de equilíbrio correta Equação 12.2.11 para torques ao longo do eixo de rotação. Use a Equação 12.2.12 para avaliar magnitudes e sentidos de torque.
4. Simplifique e resolva o sistema de equações de equilíbrio para obter quantidades desconhecidas. Neste ponto, seu trabalho envolve apenas álgebra. Lembre-se de que o número de equações deve ser o mesmo que o número de incógnitas. Se o número de incógnitas for maior do que o número de equações, o problema não poderá ser resolvido.
5. Avalie as expressões para as quantidades desconhecidas que você obteve em sua solução. Suas respostas finais devem ter valores numéricos corretos e unidades físicas corretas. Caso contrário, use as etapas anteriores para rastrear um erro até sua origem e corrigi-lo. Além disso, você pode verificar de forma independente suas respostas numéricas mudando o pivô para um local diferente e resolvendo o problema novamente, o que foi o que fizemos no Exemplo 12.1.

Observe que configurar um diagrama de corpo livre para um problema de equilíbrio de corpo rígido é o componente mais importante no processo de solução. Sem a configuração correta e um diagrama correto, você não poderá anotar as condições corretas para o equilíbrio. Observe também que um diagrama de corpo livre para um corpo rígido estendido que pode sofrer movimento rotacional é diferente de um diagrama de corpo livre para um corpo que experimenta apenas movimento translacional (como você viu nos capítulos sobre as leis do movimento de Newton). Na dinâmica translacional, um corpo é representado como seu CM, onde todas as forças no corpo estão ligadas e nenhum torque aparece. Isso não se aplica à dinâmica rotacional, onde um corpo rígido estendido não pode ser representado apenas por um ponto. A razão para isso é que, ao analisar a rotação, devemos identificar os torques que atuam no corpo, e o torque depende tanto da força atuante quanto do braço da alavanca. Aqui, o diagrama de corpo livre de um corpo rígido estendido nos ajuda a identificar torques externos.

Exemplo 12.3: O equilíbrio de torque

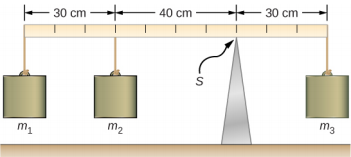
Três massas são presas a um medidor uniforme, conforme mostrado na Figura\(\PageIndex{1}\). A massa do medidor é de 150,0 g e as massas à esquerda do ponto de apoio são m ₁ = 50,0 g e m ₂ = 75,0 g. Encontre a massa m3 que equilibra o sistema quando ele está conectado na extremidade direita do manípulo e a força de reação normal no ponto de apoio quando o sistema está balanceado.

Figura\(\PageIndex{1}\): Em um balanço de torque, um feixe horizontal é apoiado em um ponto de apoio (indicado por S) e as massas são fixadas em ambos os lados do ponto de apoio. O sistema está em equilíbrio estático quando o feixe não gira. É balanceado quando o feixe permanece nivelado.

Estratégia

Para o arranjo mostrado na figura, identificamos as seguintes cinco forças atuando no medidor:

1. w ₁ = m ₁ g é o peso da massa m ₁;
2. w ₂ = m ₂ g é o peso da massa m ₂;
3. w = mg é o peso de todo o medidor;
4. w ₃ = m ₃ g é o peso da massa desconhecida m ₃;
5. F _S é a força de reação normal no ponto de apoio S.

Escolhemos um quadro de referência em que a direção do eixo y é a direção da gravidade, a direção do eixo x está ao longo do medidor e o eixo de rotação (o eixo z) é perpendicular ao eixo x e passa pelo ponto de suporte S. Em outras palavras, escolhemos o pivô no ponto em que o o medidor toca o suporte. Essa é uma escolha natural para o pivô porque esse ponto não se move quando o manípulo gira. Agora estamos prontos para configurar o diagrama de corpo livre para o medidor. Indicamos o pivô e anexamos cinco vetores representando as cinco forças ao longo da linha que representa o medidor, localizando as forças em relação ao pivô Figura\(\PageIndex{2}\). Nesse estágio, podemos identificar os braços de alavanca das cinco forças dadas as informações fornecidas no problema. Para as três massas pendentes, o problema é explícito sobre suas localizações ao longo do bastão, mas as informações sobre a localização do peso w são fornecidas implicitamente. A palavra-chave aqui é “uniforme”. Sabemos de nossos estudos anteriores que o CM de um bastão uniforme está localizado em seu ponto médio, então é aqui que fixamos o peso w, na marca de 50 cm.

Figura\(\PageIndex{2}\): Diagrama de corpo livre do medidor. O pivô é escolhido no ponto de suporte S.

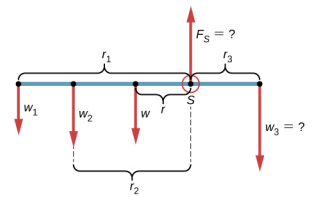
Solução

Com Figura\(\PageIndex{1}\) e Figura\(\PageIndex{2}\) como referência, começamos encontrando os braços de alavanca das cinco forças que atuam no manípulo:

\[\begin{split} r_{1} & = 30.0\; cm + 40.0\; cm = 70.0\; cm \\ r_{2} & = 40.0\; cm \\ r & = 50.0\; cm - 30.0\; cm = 20.0\; cm \\ r_{S} & = 0.0\; cm\; (because\; F_{S}\; is\; attached\; at\; the\; pivot) \\ r_{3} & = 30.0\; cm \ldotp \end{split}\]

Agora podemos encontrar os cinco torques em relação ao pivô escolhido:

\[\begin{split} \tau_{1} & = +r_{1} w_{1} \sin 90^{o} = +r_{1} m_{1} g \quad (counterclockwise\; rotation,\; positive\; sense) \\ \tau_{2} & = +r_{2} w_{2} \sin 90^{o} = +r_{2} m_{2} g \quad (counterclockwise\; rotation,\; positive\; sense) \\ \tau & = +rw \sin 90^{o} = +rmg \quad \quad \quad (gravitational\; torque) \\ \tau_{S} & = r_{S} F_{S} \sin \theta_{S} = 0 \quad \quad \quad \quad \quad (because\; r_{S} = 0\; cm) \\ \tau_{3} & = -r_{3} w_{3} \sin 90^{o} = -r_{3} m_{3} g \quad (counterclockwise\; rotation,\; negative\; sense) \end{split}\]

A segunda condição de equilíbrio (equação para os torques) para o medidor é

\[\tau_{1} + \tau_{2} + \tau + \tau_{S} + \tau_{3} = 0 \ldotp\]

Ao substituir os valores de torque nessa equação, podemos omitir os torques dando contribuições zero. Dessa forma, a segunda condição de equilíbrio é

\[+r_{1} m_{1} g + r_{2} m_{2} g + rmg - r_{3} m_{3} g = 0 \ldotp \label{12.17}\]

Selecionando a direção+y a ser paralela\(\vec{F}_{S}\), a primeira condição de equilíbrio para o manípulo é

\[-w_{1} - w_{2} - w + F_{S} - w_{3} = 0 \ldotp\]

Substituindo as forças, a primeira condição de equilíbrio se torna

\[-m_{1} g - m_{2} g - mg + F_{S} - m_{3} g = 0 \ldotp \label{12.18}\]

Resolvemos essas equações simultaneamente para os valores desconhecidos m ₃ e F _S. Na Equação\ ref {12.17}, cancelamos o fator g e reorganizamos os termos para obter

\[r_{3} m_{3} = r_{1} m_{1} + r_{2} m_{2} + rm \ldotp\]

Para obter m ₃, dividimos os dois lados por r ₃, então temos

\[\begin{split} m_{3} & = \frac{r_{1}}{r_{3}} m_{1} + \frac{r_{2}}{r_{3}} m_{2} + \frac{r}{r_{3}} m \\ & = \frac{70}{30} (50.0\; g) + \frac{40}{30} (75.0\; g) + \frac{20}{30} (150.0\; g) = 315.0 \left(\dfrac{2}{3}\right)\; g \simeq 317\; g \ldotp \end{split} \label{12.19}\]

Para encontrar a força de reação normal, reorganizamos os termos na Equação\ ref {12.18}, convertendo gramas em quilogramas:

\[\begin{split} F_{S} & = (m_{1} + m_{2} + m + m_{3}) g \\ & = (50.0 + 75.0 + 150.0 + 316.7) \times (10^{-3}\; kg) \times (9.8\; m/s^{2}) = 5.8\; N \ldotp \end{split} \label{12.20}\]

Significância

Observe que a Equação\ ref {12.17} é independente do valor de g. O equilíbrio de torque pode, portanto, ser usado para medir a massa, uma vez que variações nos valores de g na superfície da Terra não afetam essas medições. Esse não é o caso de uma balança de mola porque ela mede a força.

Exercício 12.3

Repita o Exemplo 12.3 usando a extremidade esquerda do medidor para calcular os torques; ou seja, colocando o pivô na extremidade esquerda do medidor.

No próximo exemplo, mostramos como usar a primeira condição de equilíbrio (equação para forças) na forma vetorial dada pela Equação 12.2.9 e pela Equação 12.2.10. Apresentamos esta solução para ilustrar a importância de uma escolha adequada do quadro de referência. Embora todos os quadros de referência inerciais sejam equivalentes e as soluções numéricas obtidas em um quadro sejam as mesmas de qualquer outro, uma escolha inadequada de quadro de referência pode tornar a solução bastante longa e complicada, enquanto uma escolha inteligente de quadro de referência torna a solução simples. Mostramos isso na solução equivalente para o mesmo problema. Este exemplo específico ilustra uma aplicação do equilíbrio estático à biomecânica.

Exemplo 12.4: Forças no antebraço

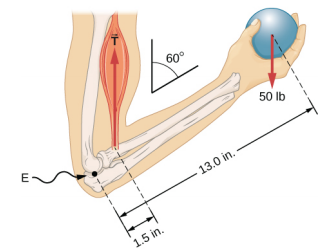
Um levantador de peso está segurando um peso de 50,0 libras (equivalente a 222,4 N) com o antebraço, conforme mostrado na Figura\(\PageIndex{3}\). Seu antebraço está posicionado em\(\beta\) = 60° em relação à parte superior do braço. O antebraço é sustentado por uma contração do músculo bíceps, o que causa um torque ao redor do cotovelo. Supondo que a tensão no bíceps aja na direção vertical dada pela gravidade, que tensão o músculo deve exercer para manter o antebraço na posição mostrada? Qual é a força na articulação do cotovelo? Suponha que o peso do antebraço seja insignificante. Dê suas respostas finais em unidades SI.

Figura\(\PageIndex{3}\): O antebraço é girado ao redor do cotovelo (E) por uma contração do músculo bíceps, o que causa tensão\(\vec{T}_{M}\).

Estratégia

Identificamos três forças atuando no antebraço: a força desconhecida\(\vec{F}\) no cotovelo; a tensão desconhecida\(\vec{T}_{M}\) no músculo; e o peso\(\vec{w}\) com magnitude w = 50 lb. Adotamos o quadro de referência com o eixo x ao longo do antebraço e o pivô no cotovelo. A direção vertical é a direção do peso, que é a mesma da parte superior do braço. O eixo x faz um ângulo\(\beta\) = 60° com a vertical. O eixo y é perpendicular ao eixo x. Agora, configuramos o diagrama de corpo livre para o antebraço. Primeiro, desenhamos os eixos, o pivô e os três vetores que representam as três forças identificadas. Em seguida, localizamos o ângulo\(\beta\) e representamos cada força por seus componentes x e y, lembrando de riscar o vetor de força original para evitar a contagem dupla. Finalmente, rotulamos as forças e seus braços de alavanca. O diagrama de corpo livre do antebraço é mostrado na Figura\(\PageIndex{4}\). Neste ponto, estamos prontos para estabelecer condições de equilíbrio para o antebraço. Cada força tem componentes x e y; portanto, temos duas equações para a primeira condição de equilíbrio, uma equação para cada componente da força líquida atuando no antebraço.

Figura\(\PageIndex{4}\): Diagrama de corpo livre para o antebraço: O pivô está localizado no ponto E (cotovelo).

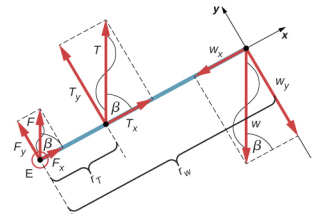
Observe que, em nosso quadro de referência, as contribuições para a segunda condição de equilíbrio (para torques) vêm apenas dos componentes y das forças porque os componentes x das forças são todos paralelos aos braços de alavanca, de modo que, para qualquer um deles, temos sen\(\theta\) = 0 na Equação 12.2.12. Para os componentes y, temos\(\theta\) = ± 90° na Equação 12.2.12. Observe também que o torque da força no cotovelo é zero porque essa força está presa ao pivô. Portanto, a contribuição para o torque líquido vem apenas dos torques de T _y e de w _y.

Solução

Vemos no diagrama de corpo livre que o componente x da força líquida satisfaz a equação

\[+F_{x} + T_{x} - w_{x} = 0 \label{12.21}\]

e o componente y da força líquida satisfaz

\[+F_{y} + T_{y} - w_{y} = 0 \ldotp \label{12.22}\]

A equação\ ref {12.21} e a Equação\ ref {12.22} são duas equações da primeira condição de equilíbrio (para forças). Em seguida, lemos no diagrama de corpo livre que o torque líquido ao longo do eixo de rotação é

\[+r_{T} T_{y} - r_{w} w_{y} = 0 \ldotp \label{12.23}\]

A equação\ ref {12.23} é a segunda condição de equilíbrio (para torques) para o antebraço. O diagrama de corpo livre mostra que os braços da alavanca são r _T = 1,5 pol. e r _w = 13,0 pol. Nesse ponto, não precisamos converter polegadas em unidades SI, pois, desde que essas unidades sejam consistentes na Equação 12.23, elas são canceladas. Usando o diagrama de corpo livre novamente, encontramos as magnitudes das forças dos componentes:

\[\begin{split} F_{x} & = F \cos \beta = F \cos 60^{o} = \frac{F}{2} \\ T_{x} & = T \cos \beta = T \cos 60^{o} = \frac{T}{2} \\ w_{x} & = w \cos \beta = w \cos 60^{o} = \frac{w}{2} \\ F_{y} & = F \sin \beta = F \sin 60^{o} = \frac{F \sqrt{3}}{2} \\ T_{y} & = T \sin \beta = T \sin 60^{o} = \frac{T \sqrt{3}}{2} \\ w_{y} & = w \sin \beta = w \sin 60^{o} = \frac{w \sqrt{3}}{2} \ldotp \end{split}\]

Substituímos essas magnitudes na Equação\ ref {12.21}, Equação\ ref {12.22} e Equação\ ref {12.23} para obter, respectivamente,

\[\begin{split} \frac{F}{2} + \frac{T}{2} - \frac{w}{2} & = 0 \\ \frac{F \sqrt{3}}{2} + \frac{T \sqrt{3}}{2} - \frac{w \sqrt{3}}{2} & = 0 \\ \frac{r_{T} T \sqrt{3}}{2} - \frac{r_{w} w \sqrt{3}}{2} & = 0 \ldotp \end{split}\]

Quando simplificamos essas equações, vemos que ficamos com apenas duas equações independentes para as duas magnitudes de força desconhecidas, F e T, porque a Equação\ ref {12.21} para o componente x é equivalente à Equação\ ref {12.22} para o componente y. Dessa forma, obtemos a primeira condição de equilíbrio para forças

\[F + T - w = 0 \label{12.24}\]

e a segunda condição de equilíbrio para torques

\[r_{T} T - r_{w} w = 0 \ldotp \label{12.25}\]

A magnitude da tensão no músculo é obtida resolvendo a Equação\ ref {12.25}:

\[T = \frac{r_{w}}{r_{T}} w =frac{13.0}{1.5} (50\; lb) = 433 \frac{1}{3}\; lb \simeq 433.3\; lb \ldotp\]

A força no cotovelo é obtida resolvendo a Equação\ ref {12.24}:

\[F = w - T = 50.0\; lb - 433.3\; lb = -383.3\; lb \ldotp\]

O sinal negativo na equação nos diz que a força real no cotovelo é antiparalela à direção de trabalho adotada para desenhar o diagrama de corpo livre. Na resposta final, convertemos as forças em unidades de força do SI. A resposta é

\[F = 383.3\; lb = 383.3(4.448\; N) = 1705\; N\; downward\]

\[T = 433.3\; lb = 433.3(4.448\; N) = 1927\; N\; upward \ldotp\]

Significância

Duas questões importantes aqui são dignas de nota. A primeira diz respeito à conversão em unidades SI, o que pode ser feito no final da solução, desde que mantenhamos a consistência nas unidades. A segunda questão importante diz respeito às articulações das dobradiças, como o cotovelo. Na análise inicial de um problema, deve-se sempre presumir que as juntas das dobradiças exercem uma força em uma direção arbitrária e, em seguida, você deve resolver todos os componentes de uma força de dobradiça de forma independente. Neste exemplo, a força do cotovelo é vertical porque o problema pressupõe que a tensão do bíceps também seja vertical. Essa simplificação, no entanto, não é uma regra geral.

Solução 2

Suponha que adotemos um quadro de referência com a direção do eixo y ao longo do peso de 50 libras e o pivô colocado no cotovelo. Nesse quadro, todas as três forças têm apenas componentes y, então temos apenas uma equação para a primeira condição de equilíbrio (para forças). Desenhamos o diagrama de corpo livre para o antebraço, conforme mostrado na Figura\(\PageIndex{5}\), indicando o pivô, as forças atuantes e seus braços de alavanca em relação ao pivô, e os ângulos\(\theta_{T}\) e (respectivamente)\(\theta_{w}\) que as forças\(\vec{T}_{M}\) e\(\vec{w}\) (respectivamente) fazem com os braços da alavanca. Na definição de torque dada pela Equação 12.2.12, o ângulo\(\theta_{T}\) é o ângulo de direção do vetor\(\vec{T}_{M}\), contado no sentido anti-horário a partir da direção radial do braço da alavanca que sempre aponta para longe do pivô. Pela mesma convenção, o ângulo\(\theta_{w}\) é medido no sentido anti-horário da direção radial do braço da alavanca até o vetor\(\vec{w}\). Feito dessa forma, os torques diferentes de zero são mais facilmente calculados substituindo-os diretamente na Equação 12.2.12 da seguinte forma:

\[\tau_{T} = r_{T} T \sin \theta_{T} = r_{T} T \sin \beta = r_{T} T \sin 60^{o} = + \frac{r_{T} T \sqrt{3}}{2}\]

\[\tau_{w} = r_{w} w \sin \theta_{w} = r_{w} w \sin (\beta + 180^{o}) = -r_{w} w \sin \beta = - \frac{r_{w} w \sqrt{3}}{2} \ldotp\]

Figura\(\PageIndex{5}\): Diagrama de corpo livre do antebraço para a solução equivalente. O pivô está localizado no ponto E (cotovelo).

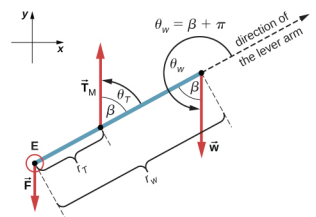
A segunda condição de equilíbrio,\(\tau_{T}\) +\(\tau_{w}\) = 0, agora pode ser escrita como

\[\frac{r_{T} T \sqrt{3}}{2} - \frac{r_{w} w \sqrt{3}}{2} = 0 \ldotp \label{12.26}\]

Do diagrama de corpo livre, a primeira condição de equilíbrio (para forças) é

\[-F + T - w = 0 \ldotp \label{12.27}\]

A equação\ ref {12.26} é idêntica à Equação\ ref {12.25} e dá o resultado T = 433,3 lb. A equação\ ref {12.27} fornece

\[F = T - w = 433.3\; lb - 50.0\; lb = 383.3\; lb\]

Vemos que essas respostas são idênticas às nossas respostas anteriores, mas a segunda opção para o quadro de referência leva a uma solução equivalente que é mais simples e rápida porque não exige que as forças sejam resolvidas em seus componentes retangulares.

Exercício 12.4

Repita o Exemplo 12.4 assumindo que o antebraço é um objeto de densidade uniforme que pesa 8,896 N.

Exemplo 12.5: Uma escada encostada em uma parede

Uma escada uniforme tem L = 5,0 m de comprimento e pesa 400,0 N. A escada repousa contra uma parede vertical escorregadia, conforme mostrado na Figura\(\PageIndex{6}\). O ângulo de inclinação entre a escada e o piso áspero é\(\beta\) = 53°. Encontre as forças de reação do piso e da parede na escada e o coeficiente de atrito estático\(\mu_{s}\) na interface da escada com o piso que impede que a escada escorregue.

Figura\(\PageIndex{6}\) Uma escada de 5,0 m de comprimento encosta-se a uma parede sem atrito.

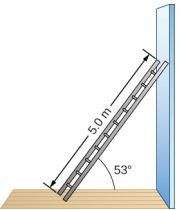
Estratégia

Podemos identificar quatro forças atuando na escada. A primeira força é a força de reação normal N do chão na direção vertical ascendente. A segunda força é a força de atrito estática f =\(\mu_{s}\) N direcionada horizontalmente ao longo do piso em direção à parede — essa força impede que a escada escorregue. Essas duas forças atuam na escada em seu ponto de contato com o chão. A terceira força é o peso w da escada, fixado em seu CM localizado a meio caminho entre suas extremidades. A quarta força é a força de reação normal F da parede na direção horizontal longe da parede, fixada no ponto de contato com a parede. Não há outras forças porque a parede é escorregadia, o que significa que não há atrito entre a parede e a escada. Com base nessa análise, adotamos o quadro de referência com o eixo y na direção vertical (paralelo à parede) e o eixo x na direção horizontal (paralelo ao chão). Nesse quadro, cada força tem um componente horizontal ou um componente vertical, mas não ambos, o que simplifica a solução. Selecionamos o pivô no ponto de contato com o piso. No diagrama de corpo livre da escada, indicamos o pivô, todas as quatro forças e seus braços de alavanca, e os ângulos entre os braços da alavanca e as forças, conforme mostrado na Figura\(\PageIndex{7}\). Com nossa escolha da localização do pivô, não há torque nem da força de reação normal N nem do atrito estático f porque ambos agem no pivô.

Figura\(\PageIndex{7}\): Diagrama de corpo livre para uma escada apoiada em uma parede sem atrito.

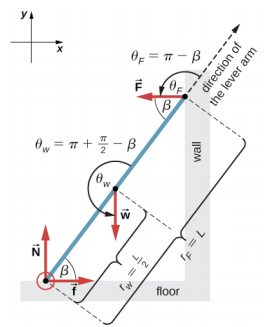
Solução

A partir do diagrama de corpo livre, a força líquida na direção x é

\[+f - F = 0 \label{12.28}\]

a força líquida na direção y é

\[+ N - w = 0 \label{12.29}\]

e o torque líquido ao longo do eixo de rotação no ponto de articulação é

\[\tau_{w} + \tau_{F} = 0 \ldotp \label{12.30}\]

onde\(\tau_{w}\) está o torque do peso w e\(\tau_{F}\) é o torque da reação F. A partir do diagrama de corpo livre, identificamos que o braço da alavanca da reação na parede é r _F = L = 5,0 m e o braço de alavanca do peso é r _w\(\frac{L}{2}\) = = 2,5 m. Com a ajuda do diagrama de corpo livre, identificamos os ângulos a serem usados na Equação 12.2.12 para torques:\(\theta_{F}\) = 180° −\(\beta\) para o torque da força de reação com a parede e\(\theta_{w}\) = 180° + (90° −\(\beta\)) para o torque devido ao peso. Agora estamos prontos para usar a Equação 12.2.12 para calcular torques:

\[\tau_{w} = r_{w} w \sin \theta_{w} = r_{w} w \sin (180^{o} + 90^{o} - \beta) = - \frac{L}{2} w \sin (90^{o} - \beta) = - \frac{L}{2} w \cos \beta\]

\[tau_{F} = r_{F} F \sin \theta_{F} = r_{F} F \sin (180^{o} - \beta) = LF \sin \beta \ldotp\]

Substituímos os torques na Equação\ ref {12.30} e resolvemos por F:

\[- \frac{L}{2} w \cos \beta + LF \sin \beta = 0 \label{12.31}\]

\[F = \frac{w}{2} \cot \beta = \frac{400.0\; N}{2} \cot 53^{o} = 150.7\; N\]

Obtemos a força de reação normal com o piso resolvendo a Equação\ ref {12.29}: N = w = 400,0 N. A magnitude do atrito é obtida resolvendo a Equação\ ref {12.28}: f = F = 150,7 N. O coeficiente de atrito estático é\(\mu_{s}\)\(\frac{f}{N}\) = =\(\frac{150.7}{400.0}\) = 0,377.

A força líquida na escada no ponto de contato com o piso é a soma vetorial da reação normal do piso e das forças de atrito estático:

\[\vec{F}_{floor} = \vec{f} + \vec{N} = (150.7\; N)(- \hat{i}) + (400.0\; N)(+ \hat{j}) = (-150.7\; \hat{i} + 400.0\; \hat{j}) N \ldotp\]

Sua magnitude é

\[F_{floor} = \sqrt{f^{2} + N^{2}} = \sqrt{150.7^{2} + 400.0^{2}}\; N = 427.4\; N\]

e sua direção é

\[\varphi = \tan^{-1} \left(\dfrac{N}{f}\right) = \tan^{-1} \left(\dfrac{400.0}{150.7}\right) = 69.3^{o}\; above\; the\; floor \ldotp\]

Devemos enfatizar aqui duas observações gerais de uso prático. Primeiro, observe que, quando escolhemos um ponto de articulação, não há expectativa de que o sistema realmente gire em torno do ponto escolhido. A escada neste exemplo não está girando, mas fica firmemente no chão; no entanto, seu ponto de contato com o piso é uma boa opção para o pivô. Em segundo lugar, observe que quando usamos a Equação 12.2.12 para o cálculo de torques individuais, não precisamos resolver as forças em seus componentes normais e paralelos em relação à direção do braço da alavanca, e não precisamos considerar uma noção do torque. Desde que o ângulo na Equação 12.2.12 seja corretamente identificado - com a ajuda de um diagrama de corpo livre - como o ângulo medido no sentido anti-horário da direção do braço da alavanca até a direção do vetor de força, a Equação 12.2.12 fornece a magnitude e a sensação do torque. Isso ocorre porque o torque é o produto vetorial do vetor do braço de alavanca cruzado com o vetor de força, e a Equação 12.2.12 expressa o componente retangular desse produto vetorial ao longo do eixo de rotação.

Significância

Esse resultado é independente do comprimento da escada porque L é cancelado na segunda condição de equilíbrio, Equação\ ref {12.31}. Não importa quão longa ou curta seja a escada, desde que seu peso seja de 400 N e o ângulo com o piso seja de 53°, nossos resultados se mantêm. Mas a escada deslizará se o torque líquido ficar negativo na Equação\ ref {12.31}. Isso acontece em alguns ângulos quando o coeficiente de atrito estático não é grande o suficiente para evitar que a escada escorregue.

Exercício 12.5

Para a situação descrita no Exemplo 12.5, determine os valores do coeficiente\(\mu_{s}\) de atrito estático para o qual a escada começa a deslizar, dado que β é o ângulo que a escada faz com o piso.

Exemplo 12.6: Forças nas dobradiças das portas

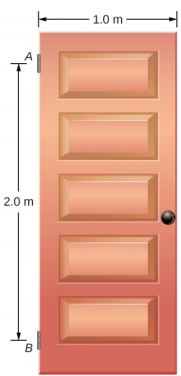
Uma porta giratória que pesa w = 400,0 N é suportada pelas dobradiças A e B para que a porta possa girar em torno de um eixo vertical que passa pelas dobradiças Figura\(\PageIndex{8}\). A porta tem uma largura de b = 1,00 m e a laje da porta tem uma densidade de massa uniforme. As dobradiças são colocadas simetricamente na borda da porta, de forma que o peso da porta seja distribuído uniformemente entre elas. As dobradiças são separadas pela distância a = 2,00 m. Encontre as forças nas dobradiças quando a porta estiver semiaberta.

Figura\(\PageIndex{8}\): Uma porta vertical giratória 400-N é suportada por duas dobradiças fixadas nos pontos A e B.

Estratégia

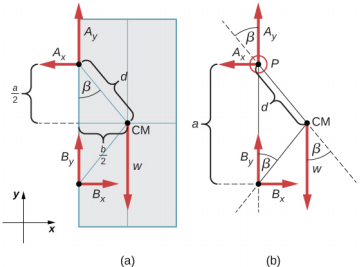
As forças que a porta exerce sobre suas dobradiças podem ser encontradas simplesmente invertendo as direções das forças que as dobradiças exercem sobre a porta. Portanto, nossa tarefa é encontrar as forças das dobradiças da porta. Três forças atuam na laje da porta: uma força desconhecida\(\vec{A}\) da dobradiça A, uma força desconhecida\(\vec{B}\) da dobradiça B e o peso conhecido\(\vec{w}\) fixado no centro de massa da laje da porta. O CM está localizado no centro geométrico da porta porque a laje tem uma densidade de massa uniforme. Adotamos uma estrutura retangular de referência com o eixo y ao longo da direção da gravidade e o eixo x no plano da laje, conforme mostrado no painel (a) da Figura\(\PageIndex{9}\), e resolvemos todas as forças em seus componentes retangulares. Dessa forma, temos quatro componentes desconhecidos: dois componentes de força\(\vec{A}\) (A _x e A _y) e dois componentes de força\(\vec{B}\) (B _x e B _y). No diagrama de corpo livre, representamos as duas forças nas dobradiças por seus componentes vetoriais, cujas orientações assumidas são arbitrárias. Como existem quatro incógnitas (A _x, B _x, A _y e B _y), devemos configurar quatro equações independentes. Uma equação é a condição de equilíbrio para forças na direção x. A segunda equação é a condição de equilíbrio para forças na direção y. A terceira equação é a condição de equilíbrio para torques em rotação em torno de uma dobradiça. Como o peso é distribuído uniformemente entre as dobradiças, temos a quarta equação, A _y = B _y. Para configurar as condições de equilíbrio, desenhamos um diagrama de corpo livre e escolhemos o ponto de articulação na dobradiça superior, conforme mostrado no painel (b) da Figura\(\PageIndex{9}\). Finalmente, resolvemos as equações para os componentes de força desconhecidos e encontramos as forças.

Figura\(\PageIndex{9}\): (a) Geometria e (b) diagrama de corpo livre para a porta.

Solução

A partir do diagrama de corpo livre da porta, temos a primeira condição de equilíbrio para forças:

na direção x, $$-A_ {x} + B_ {x} = 0\ Rightarrow A_ {x} + B_ {x} $na direção y, $$+ A_ {y} + B_ {y} - w = 0\ Rightarrow A_ {y} = B_ {y} =\ frac {w} {2} =\ frac {400.0\; N} {2} = 200,0\; N\ ldotp\]

Selecionamos o pivô no ponto P (dobradiça superior, de acordo com o diagrama de corpo livre) e escrevemos a segunda condição de equilíbrio para torques em rotação em torno do ponto P:

pivô em P: $$\ tau_ {w} +\ tau_ {Bx} +\ tau_ {By} = 0\ ldotp\ label {12.32}\]

Usamos o diagrama de corpo livre para encontrar todos os termos nesta equação:

\[\begin{split} \tau_{w} & = dw \sin (- \beta) = -dw \sin \beta = -dw \frac{\frac{b}{2}}{d} = -w \frac{b}{2} \\ \tau_{Bx} & = a B_{x} \sin 90^{o} = + a B_{x} \\ \tau_{By} & = a B_{y} \sin 180^{o} = 0 \ldotp \end{split}\]

Ao avaliar o pecado\(\beta\), usamos a geometria do triângulo mostrada na parte (a) da figura. Agora substituímos esses torques na Equação\ ref {12.32} e calculamos B _x:

pivô em P: $$-w\ frac {b} {2} + a B_ {x} = 0\ Rightarrow B_ {x} = w\ frac {b} {2a} = (400.0\; N)\ frac {1} {2\;\ cdotp 2} = 100,0\; N\ ldotp\]

Portanto, as magnitudes das forças dos componentes horizontais são A _x = B _x = 100,0 N. As forças na porta são

na dobradiça superior: $$\ vec {F} _ {A\; na\; porta} = -100.0\; N\;\ hat {i} + 200.0\; N\;\ hat {j} $na dobradiça inferior: $$\ vec {F} _ {B\; na\; porta} = +100,0\; N\;\ hat {i} + 200.0 0\; N\;\ hat {j}\ ldotp\]

As forças nas dobradiças são encontradas na terceira lei de Newton como

na dobradiça superior: $$\ vec {F} _ {porta\; on\; A} = 100.0\; N\;\ hat {i} - 200.0\; N\;\ hat {j} $na dobradiça inferior: $$\ vec {F} _ {door\; on\; B} = - 100.0\; N\;\ hat {i} - 200.0\; N\;\ hat {j}\ ldotp\]

Significância

Observe que se o problema fosse formulado sem a suposição de que o peso estivesse igualmente distribuído entre as duas dobradiças, não seríamos capazes de resolvê-lo porque o número de incógnitas seria maior do que o número de equações que expressam condições de equilíbrio.

Exercício 12.6

Resolva o problema no Exemplo 12.6 tomando a posição do pivô no centro da massa.

Exercício 12.7

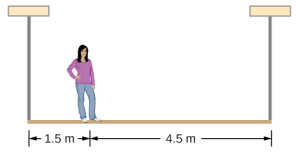
Uma pessoa de 50 kg fica a 1,5 m de distância de uma extremidade de um andaime uniforme de 6,0 m de comprimento e massa de 70,0 kg. Encontre as tensões nas duas cordas verticais que sustentam o andaime.

Exercício 12.8

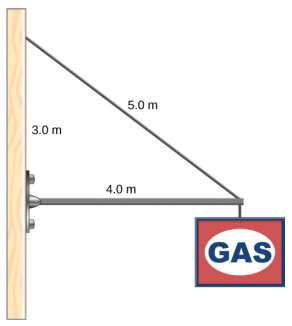
Uma placa de 400.0-N está pendurada na extremidade de um suporte uniforme. O suporte tem 4,0 m de comprimento e pesa 600,0 N. O suporte é suportado por uma dobradiça na parede e por um cabo cuja outra extremidade é amarrada à parede em um ponto 3,0 m acima da extremidade esquerda do suporte. Encontre a tensão no cabo de suporte e a força da dobradiça no suporte.