12.2: Condições para o equilíbrio estático
- Page ID
- 185216
- Identifique as condições físicas do equilíbrio estático.
- Desenhe um diagrama de corpo livre para um corpo rígido acionado por forças.
- Explique como as condições para o equilíbrio nos permitem resolver problemas estáticos.
Dizemos que um corpo rígido está em equilíbrio quando sua aceleração linear e angular são zero em relação a um quadro de referência inercial. Isso significa que um corpo em equilíbrio pode estar se movendo, mas, nesse caso, suas velocidades lineares e angulares devem ser constantes. Dizemos que um corpo rígido está em equilíbrio estático quando está em repouso em nosso quadro de referência selecionado. Observe que a distinção entre o estado de repouso e um estado de movimento uniforme é artificial, ou seja, um objeto pode estar em repouso em nosso quadro de referência selecionado, mas para um observador se movendo em velocidade constante em relação ao nosso quadro, o mesmo objeto parece estar em movimento uniforme com velocidade constante. Como o movimento é relativo, o que está em equilíbrio estático para nós está em equilíbrio dinâmico para o observador em movimento e vice-versa. Como as leis da física são idênticas para todos os quadros de referência inerciais, em um quadro de referência inercial, não há distinção entre equilíbrio estático e equilíbrio.
De acordo com a segunda lei do movimento de Newton, a aceleração linear de um corpo rígido é causada por uma força líquida atuando sobre ele, ou
\[\sum_{k} \vec{F}_{k} = m \vec{a}_{CM} \ldotp \label{12.1}\]
Aqui, a soma é de todas as forças externas que atuam no corpo, onde m é sua massa e\(\vec{a}_{CM}\) é a aceleração linear de seu centro de massa (um conceito que discutimos em Momento Linear e Colisões sobre momento linear e colisões). Em equilíbrio, a aceleração linear é zero. Se definirmos a aceleração para zero na Equação\ ref {12.1}, obtemos a seguinte equação:
A primeira condição de equilíbrio para o equilíbrio estático de um corpo rígido expressa o equilíbrio translacional:
\[\sum_{k} \vec{F}_{k} = \vec{0} \ldotp \label{12.2}\]
A primeira condição de equilíbrio, Equação\ ref {12.2}, é a condição de equilíbrio das forças, que encontramos ao estudar as aplicações das leis de Newton.
Essa equação vetorial é equivalente às três equações escalares a seguir para os componentes da força líquida:
\[\sum_{k} F_{kx} = 0,\; \sum_{k} F_{ky} = 0,\; \sum_{k} F_{kz} = 0 \ldotp \label{12.3}\]
Analogamente à Equação\ ref {12.1}, podemos afirmar que a aceleração rotacional\(\vec{\alpha}\) de um corpo rígido em torno de um eixo fixo de rotação é causada pelo torque líquido atuando no corpo, ou
\[\sum_{k} \vec{\tau}_{k} = I \vec{\alpha} \ldotp \label{12.4}\]
Aqui eu estou a inércia rotacional do corpo em rotação em torno desse eixo e a soma é sobre todos os torques\(\vec{\tau}_{k}\) de forças externas na Equação\ ref {12.2}. Em equilíbrio, a aceleração rotacional é zero. Ao definir como zero o lado direito da Equação\ ref {12.4}, obtemos a segunda condição de equilíbrio:
A segunda condição de equilíbrio para o equilíbrio estático de um corpo rígido expressa o equilíbrio rotacional:
\[\sum_{k} \vec{\tau}_{k} = \vec{0} \ldotp \label{12.5}\]
A segunda condição de equilíbrio, Equação\ ref {12.5}, é a condição de equilíbrio para torques que encontramos quando estudamos a dinâmica rotacional. É importante notar que essa equação para equilíbrio geralmente é válida para equilíbrio rotacional sobre qualquer eixo de rotação (fixo ou não). Novamente, essa equação vetorial é equivalente a três equações escalares para os componentes vetoriais do torque líquido:
\[\sum_{k} \tau_{kx} = 0,\; \sum_{k} \tau_{ky} = 0,\; \sum_{k} \tau_{kz} = 0 \ldotp \label{12.6}\]
A segunda condição de equilíbrio significa que, em equilíbrio, não há torque externo líquido que cause rotação em torno de qualquer eixo. A primeira e a segunda condições de equilíbrio são declaradas em um quadro de referência específico. A primeira condição envolve apenas forças e, portanto, é independente da origem do quadro de referência. No entanto, a segunda condição envolve torque, que é definido como um produto cruzado\(\vec{\tau}_{k} = \vec{r}_{k} \times \vec{F}_{k}\), em que o vetor de posição em\(\vec{r}_{k}\) relação ao eixo de rotação do ponto onde a força é aplicada entra na equação. Portanto, o torque depende da localização do eixo no quadro de referência. No entanto, quando as condições de equilíbrio rotacional e translacional se mantêm simultaneamente em um quadro de referência, elas também se mantêm em qualquer outro quadro de referência inercial, de modo que o torque líquido sobre qualquer eixo de rotação ainda é zero. A explicação para isso é bastante simples.
Suponha que vetor\(\vec{R}\) seja a posição da origem de um novo quadro inercial de referência S′no antigo quadro inercial de referência S. Do nosso estudo de movimento relativo, sabemos que no novo quadro de referência S′, o vetor\(\vec{r}′_{k}\) de posição do ponto onde a força\(\vec{F}_{k}\) é aplicada é relacionado\(\vec{r}_{k}\) por meio da equação
\[\vec{r}'_{k} = \vec{r}_{k} - \vec{R} \ldotp\]
Agora, podemos somar todos os torques\(\vec{\tau}'_{k} = \vec{r}'_{k} \times \vec{F}_{k}\) de todas as forças externas em um novo quadro de referência, S':
\[\sum_{k} \vec{\tau}'_{k} = \sum_{k} \vec{r}'_{k} \times \vec{F}_{k} = \sum_{k} (\vec{r}_{k} - \vec{R}) \times \vec{F}_{k} = \sum_{k} \vec{r}_{k} \times \vec{F}_{k} - \sum_{k} \vec{R} \times \vec{F}_{k} = \sum \vec{\tau}_{k} - \vec{R} \times \sum_{k} \vec{F}_{k} = \vec{0} \ldotp\]
Na etapa final dessa cadeia de raciocínio, usamos o fato de que em equilíbrio no antigo quadro de referência, S, o primeiro termo desaparece por causa da Equação\ ref {12.5} e o segundo termo desaparece por causa da Equação\ ref {12.2}. Portanto, vemos que o torque líquido em qualquer quadro inercial de referência S′s é zero, desde que ambas as condições para o equilíbrio se mantenham em um quadro inercial de referência\ ref {S}.
A implicação prática disso é que, ao aplicar condições de equilíbrio para um corpo rígido, somos livres para escolher qualquer ponto como a origem do quadro de referência. Nossa escolha do quadro de referência é ditada pelas especificidades físicas do problema que estamos resolvendo. Em um quadro de referência, a forma matemática das condições de equilíbrio pode ser bastante complicada, enquanto em outro quadro, as mesmas condições podem ter uma forma matemática mais simples e fácil de resolver. A origem de um quadro de referência selecionado é chamada de ponto de articulação.
No caso mais geral, as condições de equilíbrio são expressas pelas seis equações escalares (Equações\ ref {12.3} e\ ref {12.6}). Para problemas de equilíbrio planar com rotação em torno de um eixo fixo, que consideramos neste capítulo, podemos reduzir o número de equações para três. O procedimento padrão é adotar um quadro de referência em que o eixo z é o eixo de rotação. Com essa escolha de eixo, o torque líquido tem apenas um componente z, todas as forças que têm torques diferentes de zero estão no plano xy e, portanto, as contribuições para o torque líquido vêm apenas dos componentes x e y das forças externas. Assim, para problemas planares com o eixo de rotação perpendicular ao plano xy, temos as seguintes três condições de equilíbrio para forças e torques:
\[F_{1x} + F_{2x} + \cdots + F_{Nx} = 0 \label{12.7}\]
\[F_{1y} + F_{2y} + \cdots + F_{Ny} = 0 \label{12.8}\]
\[\tau_{1} + \tau_{2} + \cdots + \tau_{N} = 0 \label{12.9}\]
onde a soma é sobre todas as N forças externas que atuam sobre o corpo e sobre seus torques. Na Equação\ ref {12.9}, simplificamos a notação descartando o subscrito z, mas entendemos aqui que a soma é sobre todas as contribuições ao longo do eixo z, que é o eixo de rotação. Na Equação\ ref {12.9}, o componente z do torque\(\vec{\tau}_{k}\) da força\(\vec{F}_{k}\) é
\[\tau_{k} = r_{k} F_{k} \sin \theta \label{12.10}\]
onde r k é o comprimento do braço da alavanca da força e F k é a magnitude da força (como você viu em Rotação de Eixo Fixo). O ângulo\(\theta\) é o ângulo entre os vetores\(\vec{r}_{k}\) e\(\vec{F}_{k}\), medindo de vetor\(\vec{r}_{k}\) para vetor\(\vec{F}_{k}\) no sentido anti-horário (Figura\(\PageIndex{1}\)). Ao usar a Equação\ ref {12.10}, geralmente calculamos a magnitude do torque e atribuímos seu sentido como positivo (+) ou negativo (−), dependendo da direção de rotação causada apenas por esse torque. Na Equação\ ref {12.9}, o torque líquido é a soma dos termos, com cada termo calculado a partir da Equação\ ref {12.10}, e cada termo deve ter o sentido correto. Da mesma forma, na Equação\ ref {12.7}, atribuímos o sinal + para forçar componentes na direção + x e o sinal − a componentes na direção − x. A mesma regra deve ser seguida consistentemente na Equação\ ref {12.8}, ao calcular componentes de força ao longo do eixo y.
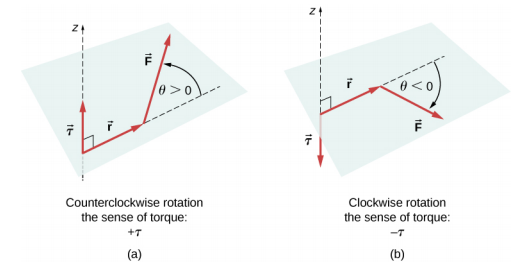
Veja esta demonstração para ver duas forças atuando em um quadrado rígido em duas dimensões. Em todos os momentos, as condições de equilíbrio estático dadas pela Equação\ ref {12.7} até a Equação\ ref {12.9} são satisfeitas. Você pode variar as magnitudes das forças e de seus braços de alavanca e observar o efeito que essas mudanças têm no quadrado.
Em muitas situações de equilíbrio, uma das forças que atuam no corpo é seu peso. Em diagramas de corpo livre, o vetor de peso é anexado ao centro de gravidade do corpo. Para todos os fins práticos, o centro de gravidade é idêntico ao centro de massa, como você aprendeu em Momento linear e colisões sobre momento linear e colisões. Somente em situações em que um corpo tem uma grande extensão espacial para que o campo gravitacional não seja uniforme em todo o seu volume, o centro de gravidade e o centro de massa estão localizados em pontos diferentes. Em situações práticas, no entanto, mesmo objetos tão grandes quanto edifícios ou navios de cruzeiro estão localizados em um campo gravitacional uniforme na superfície da Terra, onde a aceleração devido à gravidade tem uma magnitude constante de g = 9,8 m/s 2. Nessas situações, o centro de gravidade é idêntico ao centro de massa. Portanto, ao longo deste capítulo, usamos o centro de massa (CM) como o ponto em que o vetor de peso está anexado. Lembre-se de que o CM tem um significado físico especial: quando uma força externa é aplicada a um corpo exatamente em seu CM, o corpo como um todo sofre movimento translacional e essa força não causa rotação.
Quando o CM está localizado fora do eixo de rotação, ocorre um torque gravitacional líquido em um objeto. O torque gravitacional é o torque causado pelo peso. Esse torque gravitacional pode girar o objeto se não houver suporte presente para equilibrá-lo. A magnitude do torque gravitacional depende da distância do pivô em que o CM está localizado. Por exemplo, no caso de um caminhão basculante (Figura\(\PageIndex{2}\)), o pivô está localizado na linha em que os pneus entram em contato com a superfície da estrada. Se o CM estiver localizado bem acima da superfície da estrada, o torque gravitacional pode ser grande o suficiente para virar o caminhão. Carros de passageiros com CM baixo, próximos ao pavimento, são mais resistentes a tombamentos do que caminhões.
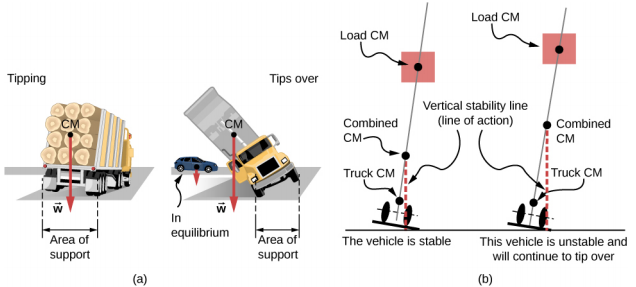
Se você inclinar uma caixa de forma que uma borda permaneça em contato com a mesa abaixo dela, uma borda da base do suporte se tornará um pivô. Enquanto o centro de gravidade da caixa permanecer sobre a base do suporte, o torque gravitacional gira a caixa de volta em direção à sua posição original de equilíbrio estável. Quando o centro de gravidade se move para fora da base de suporte, o torque gravitacional gira a caixa na direção oposta e a caixa rola. Veja esta demonstração para experimentar as posições estáveis e instáveis de uma caixa.
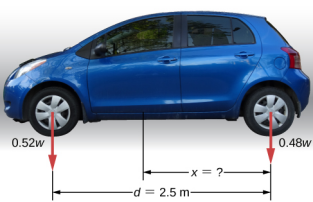
Um carro de passageiros com uma distância entre eixos de 2,5 m tem 52% de seu peso nas rodas dianteiras em terreno plano, conforme ilustrado na Figura 12.4. Onde está localizado o CM deste carro em relação ao eixo traseiro?
Estratégia
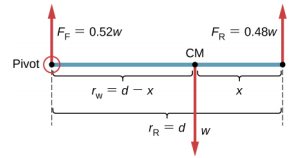
Não sabemos o peso w do carro. Tudo o que sabemos é que quando o carro repousa em uma superfície nivelada, 0,52w empurra para baixo na superfície nos pontos de contato das rodas dianteiras e 0,48w empurra para baixo na superfície nos pontos de contato das rodas traseiras. Além disso, os pontos de contato são separados uns dos outros pela distância d = 2,5 m. Nesses pontos de contato, o carro experimenta forças de reação normais com magnitudes F F = 0,52w e F R = 0,48w nos eixos dianteiro e traseiro, respectivamente. Também sabemos que o carro é um exemplo de uma carroceria rígida em equilíbrio cujo peso inteiro w atua em seu CM. O CM está localizado em algum lugar entre os pontos onde as forças de reação normais atuam, em algum lugar a uma distância x do ponto em que F R atua. Nossa tarefa é encontrar x. Assim, identificamos três forças atuando na carroceria (o carro) e podemos desenhar um diagrama de corpo livre para o corpo rígido estendido, conforme mostrado na Figura\(\PageIndex{4}\).
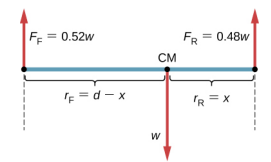
Estamos quase prontos para anotar as condições de equilíbrio Equation\ ref {12.7} até Equation\ ref {12.9} para o carro, mas primeiro devemos decidir sobre o quadro de referência. Suponha que escolhamos o eixo x ao longo do comprimento do carro, o eixo y vertical e o eixo z perpendicular a esse plano xy. Com essa opção, precisamos apenas escrever Equation\ ref {12.7} e Equation\ ref {12.9} porque todos os componentes y são idênticos a zero. Agora precisamos decidir a localização do ponto de articulação. Podemos escolher qualquer ponto como a localização do eixo de rotação (eixo z). Suponha que coloquemos o eixo de rotação em CM, conforme indicado no diagrama de carroceria livre do carro. Neste ponto, estamos prontos para escrever as condições de equilíbrio do carro.
Solução
Cada condição de equilíbrio contém apenas três termos porque há N = 3 forças atuando no carro. A primeira condição de equilíbrio, Equação\ ref {12.7}, diz
\[+F_{F} - w + F_{R} = 0 \ldotp \label{12.11}\]
Essa condição é trivialmente satisfeita porque quando substituímos os dados, a Equação\ ref {12.11} se torna +0,52w − w + 0,48w = 0. A segunda condição de equilíbrio, Equação\ ref {12.9}, diz
\[\tau_{F} + \tau_{w} + \tau_{R} = 0 \label{12.12}\]
onde\(\tau_{F}\) é o torque da força F F,\(\tau_{w}\) é o torque gravitacional da força w e\(\tau_{R}\) é o torque da força F R. Quando o pivô está localizado em CM, o torque gravitacional é idêntico a zero porque o braço de alavanca do peso em relação a um eixo que passa por CM é zero. As linhas de ação de ambas as forças de reação normais são perpendiculares aos braços da alavanca, então na Equação\ ref {12.10}, temos |sin\(\theta\) | = 1 para ambas as forças. No diagrama de corpo livre, lemos que o torque\(\tau_{F}\) causa rotação no sentido horário em torno do pivô em CM, então seu sentido é negativo; e o torque\(\tau_{R}\) causa rotação no sentido anti-horário em torno do pivô em CM, então seu sentido é positivo. Com essas informações, escrevemos a segunda condição de equilíbrio como
\[-r_{F} F_{F} + r_{R} F_{R} = 0 \ldotp \label{12.13}\]
Com a ajuda do diagrama de corpo livre, identificamos as magnitudes de força F R = 0,48w e F F = 0,52w, e seus braços de alavanca correspondentes r R = x e r F = d − x. Agora podemos escrever a segunda condição de equilíbrio, Equação\ ref {12.13}, explicitamente em termos do distância desconhecida x:
\[-0.52(d - x)w + 0.48xw = 0 \ldotp \label{12.14}\]
Aqui, o peso w é cancelado e podemos resolver a equação para a posição desconhecida x do CM. A resposta é x = 0,52d = 0,52 (2,5 m) = 1,3 m. Solução A escolha do pivô na posição do eixo dianteiro não altera o resultado. O diagrama de corpo livre para essa localização do pivô é apresentado na Figura 12.6. Para essa escolha de ponto de articulação, a segunda condição de equilíbrio é
\[-r_{w} w + r_{R} F_{R} = 0 \ldotp \label{12.15}\]
Quando substituímos as quantidades indicadas no diagrama, obtemos
\[-(d - x)w + 0.48dw = 0 \ldotp \label{12.16}\]
A resposta obtida ao resolver a Equação\ ref {12.13} é, novamente, x = 0,52d = 1,3 m.
Significância
Este exemplo mostra que, ao resolver problemas de equilíbrio estático, temos a liberdade de escolher a localização do pivô. Para diferentes escolhas do ponto de articulação, temos diferentes conjuntos de condições de equilíbrio a serem resolvidas. No entanto, todas as escolhas levam à mesma solução para o problema.
Resolva o Exemplo 12.1 escolhendo o pivô na localização do eixo traseiro.
Explique qual das seguintes situações satisfaz as duas condições de equilíbrio: (a) uma bola de tênis que não gira enquanto viaja no ar; (b) um pelicano que está planando no ar a uma velocidade constante em uma altitude; ou (c) um virabrequim no motor de um carro estacionado.
Um caso especial de equilíbrio estático ocorre quando todas as forças externas em um objeto agem no eixo de rotação ou ao longo dele ou quando a extensão espacial do objeto pode ser ignorada. Nesse caso, o objeto pode ser tratado com eficácia como uma massa pontual. Nesse caso especial, não precisamos nos preocupar com a segunda condição de equilíbrio, Equação\ ref {12.9}, porque todos os torques são idênticos a zero e a primeira condição de equilíbrio (para forças) é a única condição a ser satisfeita. O diagrama de corpo livre e a estratégia de resolução de problemas para esse caso especial foram descritos nas Leis do Movimento e Aplicações das Leis de Newton. Você verá uma situação de equilíbrio típica envolvendo apenas a primeira condição de equilíbrio no próximo exemplo.
Assista a esta demonstração para ver três pesos que são conectados por cordas sobre polias e amarrados juntos em um nó. Você pode experimentar os pesos para ver como eles afetam a posição de equilíbrio do nó e, ao mesmo tempo, ver a representação do diagrama vetorial da primeira condição de equilíbrio em ação.
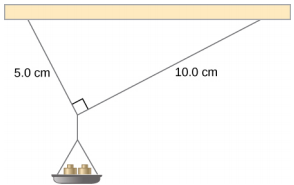
Uma pequena panela de massa de 42,0 g é suportada por duas cordas, conforme mostrado na Figura 12.7. A tensão máxima que a corda pode suportar é de 2,80 N. A massa é adicionada gradualmente à panela até que uma das cordas se encaixe. Qual corda é essa? Quanta massa deve ser adicionada para que isso ocorra?
Estratégia
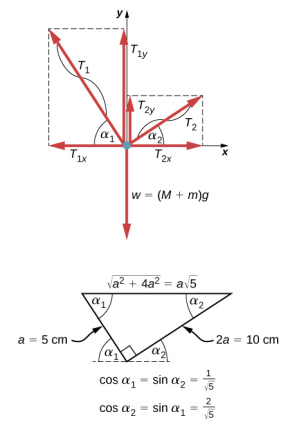
Este sistema mecânico composto por cordas, massas e a panela está em equilíbrio estático. Especificamente, o nó que amarra as cordas à panela está em equilíbrio estático. O nó pode ser tratado como um ponto; portanto, precisamos apenas da primeira condição de equilíbrio. As três forças que puxam o nó são a tensão\(\vec{T}_{1}\) na corda de 5,0 cm, a tensão\(\vec{T}_{2}\) na corda de 10,0 cm e o peso\(\vec{w}\) da panela que segura as massas. Adotamos um sistema de coordenadas retangulares com o eixo y apontando para o lado oposto à direção da gravidade e desenhamos o diagrama de corpo livre para o nó (veja a Figura 12.8). Para encontrar os componentes de tensão, devemos identificar os ângulos de direção\(\alpha_{1}\) e\(\alpha_{2}\) que as cordas formam com a direção horizontal que é o eixo x. Como você pode ver na Figura 12.7, as cordas formam os dois lados de um triângulo reto. Podemos usar o teorema de Pitágoras para resolver esse triângulo, mostrado na Figura 12.8, e encontrar o seno e o cosseno dos ângulos\(\alpha_{1}\)\(\alpha_{2}\) e. Então, podemos resolver as tensões em seus componentes retangulares, substituir na primeira condição pelo equilíbrio (Equação\ ref {12.7} e Equação\ ref {12.8}) e resolver as tensões nas cordas. A corda com maior tensão se quebrará primeiro.
Solução
O peso que w puxa no nó é devido à massa M da panela e à massa m adicionada à panela, ou w = (M + m) g. Com a ajuda do diagrama de corpo livre na Figura 12.8, podemos configurar as condições de equilíbrio para o nó:
na direção x,\[-T_{1x} + T_{2x} = 0\] na direção y,\[+T_{1y} + T_{2y} - w = 0 \ldotp\]
A partir do diagrama de corpo livre, as magnitudes dos componentes nessas equações são
\[\begin{split} T_{1x} & = T_{1} \cos \alpha_{1} = \frac{T_{1}}{\sqrt{5}},\quad T_{1y} = T_{1} \sin \alpha_{1} = \frac{2T_{1}}{\sqrt{5}} \\ T_{2x} & = T_{2} \cos \alpha_{2} = \frac{2T_{2}}{\sqrt{5}},\quad T_{2y} = T_{2} \sin \alpha_{2} = \frac{T_{2}}{\sqrt{5}} \ldotp \end{split}\]
Substituímos esses componentes nas condições de equilíbrio e simplificamos. Em seguida, obtemos duas equações de equilíbrio para as tensões:
na direção x,\[T_{1} = 2T_{2}\]
na direção y,\[\frac{2T_{1}}{\sqrt{5}} + \frac{T_{2}}{\sqrt{5}} = (M + m)g \ldotp\]
A equação de equilíbrio para a direção x nos diz que a tensão T 1 na corda de 5,0 cm é o dobro da tensão T 2 na corda de 10,0 cm. Portanto, a corda mais curta se encaixará. Quando usamos a primeira equação para eliminar T 2 da segunda equação, obtemos a relação entre a massa m na panela e a tensão T 1 na corda mais curta:
\[\frac{2.5T_{1}}{\sqrt{5}} = (M + m)g \ldotp\]
A corda se rompe quando a tensão atinge o valor crítico de T 1 = 2,80 N. A equação anterior pode ser resolvida para a massa crítica m que quebra a corda:
\[m = \frac{2.5}{\sqrt{5}} \frac{T_{1}}{g} - M = \frac{2.5}{\sqrt{5}} \frac{2.80\; N}{9.8\; m/s^{2}} - 0.042\; kg = 0.277\; kg = 277.0\; g \ldotp\]
Significância
Suponha que o sistema mecânico considerado neste exemplo esteja preso a um teto dentro de um elevador subindo. Enquanto o elevador subir a uma velocidade constante, o resultado permanece o mesmo porque o peso w não muda. Se o elevador subir com a aceleração, a massa crítica é menor porque o peso de M + m se torna maior em um peso aparente devido à aceleração do elevador. Ainda assim, em todos os casos, a corda mais curta quebra primeiro.


