Skip to main content
Global

11.5: Precessão de um giroscópio

  1. Last updated
  2. Save as PDF
  • Page ID
    184781

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    objetivos de aprendizagem

    • Descreva os processos físicos subjacentes ao fenômeno da precessão
    • Calcule a velocidade angular de precessão de um giroscópio

    \(\PageIndex{1}\)A figura mostra um giroscópio, definido como um disco giratório no qual o eixo de rotação é livre para assumir qualquer orientação. Ao girar, a orientação do eixo de rotação não é afetada pela orientação do corpo que o envolve. A carroceria ou veículo que envolve o giroscópio pode ser movido de um lugar para outro e a orientação do eixo de rotação permanecerá a mesma. Isso torna os giroscópios muito úteis na navegação, especialmente onde bússolas magnéticas não podem ser usadas, como em naves espaciais tripuladas e não tripuladas, mísseis balísticos intercontinentais, veículos aéreos não tripulados e satélites como o Telescópio Espacial Hubble.

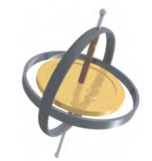
    Desenho de um giroscópio, que consiste em um disco que pode girar em um eixo, perpendicular ao plano do disco e através de seu centro. Dois anéis cercam o giroscópio. Um está preso ao eixo acima e abaixo do disco, e o outro está preso ao primeiro anel e está no plano do disco, de forma que esse segundo anel seja concêntrico ao disco.
    Figura\(\PageIndex{1}\): Um giroscópio consiste em um disco giratório em torno de um eixo que é livre para assumir qualquer orientação.

    Ilustramos a precessão de um giroscópio com um exemplo de tampo nas próximas duas figuras. Se o topo for colocado em uma superfície plana próxima à superfície da Terra em um ângulo com a vertical e não estiver girando, ele cairá, devido à força da gravidade que produz um torque atuando em seu centro de massa. Isso é mostrado na Figura\(\PageIndex{2a}\). No entanto, se a parte superior estiver girando em seu eixo, em vez de tombar devido a esse torque, ela recessa a vertical, mostrada em\(\PageIndex{2b}\). Isso se deve ao torque no centro de massa, que proporciona a mudança no momento angular.

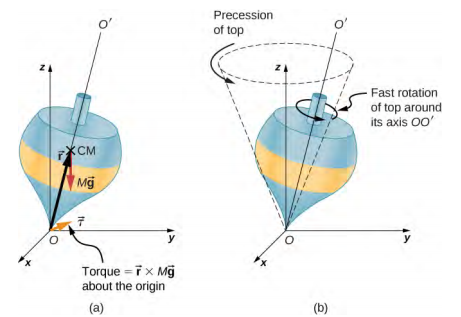
    Figura a: Um sistema de coordenadas x y z é exibido, com x fora da página, y à direita e z para cima. A origem é o ponto O. Uma parte superior é mostrada com seu ponto na origem e seu eixo inclinado para longe do eixo vertical z. O eixo do topo é a linha O O prime. O vetor r se estende da origem até o centro da massa, rotulado como C M, do topo. A força M g atua para baixo no centro da massa. O torque sobre a origem é igual ao vetor r cruzado com o vetor M g. Esse torque é um vetor no plano x y, perpendicular ao vetor r. Figura b: A coordenada x y z e a parte superior são mostradas. A parte superior é novamente inclinada para longe do eixo z e está girando rapidamente no sentido anti-horário em torno do eixo principal O O, conforme visto de cima. A precessão do topo traça um círculo no sentido anti-horário visto de cima, centrado no eixo z. O cone varrido pela precessão do topo é indicado usando linhas tracejadas.
    Figura\(\PageIndex{2}\): (a) Se a parte superior não estiver girando, há um torque\(\vec{r} \times M\vec{g}\) sobre a origem e a parte superior cai. (b) Se a parte superior estiver girando em torno de seu eixo OO', ela não cai, mas recessa em torno do eixo z.

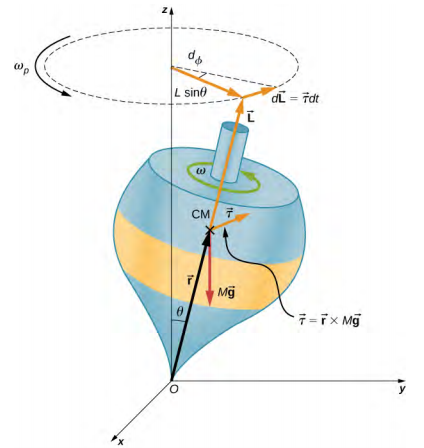
    A figura\(\PageIndex{3}\) mostra as forças atuando em um pião. O torque produzido é perpendicular ao vetor de momento angular. Isso muda a direção do vetor de momento angular de\(\vec{L}\) acordo com d\(\vec{L}\) =\(\vec{\tau}\) dt, mas não sua magnitude. O topo precessa em torno de um eixo vertical, pois o torque é sempre horizontal e perpendicular\(\vec{L}\) a. Se a parte superior não estiver girando, ela adquire impulso angular na direção do torque e gira em torno de um eixo horizontal, caindo exatamente como esperávamos.

    Um sistema de coordenadas x y z é exibido, com x fora da página, y à direita e z para cima. A origem é o ponto O. Um topo é mostrado com seu ponto na origem e seu eixo inclinado por um ângulo teta distante do eixo vertical z, no sentido horário, conforme o vemos. O vetor r se estende da origem até o centro da massa, rotulado como C M, do topo. A força M g atua para baixo no centro da massa. O torque, tau, sobre a origem é igual ao vetor r cruzado com o vetor M g. Esse torque é um vetor no plano x y, perpendicular ao vetor r, na página. A velocidade angular, ômega, da parte superior é no sentido anti-horário, vista de cima. O momento angular, L, está na mesma direção do vetor r, inclinado para cima ao longo do eixo da parte superior. O círculo traçado pela precessão do topo é mostrado como um círculo horizontal acima do topo. A velocidade angular de precessão omega sub p é no sentido anti-horário, conforme vista de cima. O raio do círculo de precessão é L sine theta. O vetor d L é tangente ao círculo, apontando para a página, e é igual ao vetor tau d t. O triângulo formado L seno teta e d L é mostrado, e o ângulo em frente a d L é rotulado como d phi.
    Figura\(\PageIndex{3}\): A força da gravidade atuando no centro de massa produz um torque\(\vec{\tau}\) na direção perpendicular\(\vec{L}\) a. A magnitude de\(\vec{L}\) não muda, mas sua direção sim, e o topo precessa sobre o eixo z.

    Podemos experimentar esse fenômeno em primeira mão segurando uma roda giratória de bicicleta e tentando girá-la em torno de um eixo perpendicular ao eixo de rotação. Conforme mostrado na Figura\(\PageIndex{4}\), a pessoa aplica forças perpendiculares ao eixo de rotação na tentativa de girar a roda, mas, em vez disso, o eixo da roda começa a mudar de direção para a esquerda devido ao torque aplicado.

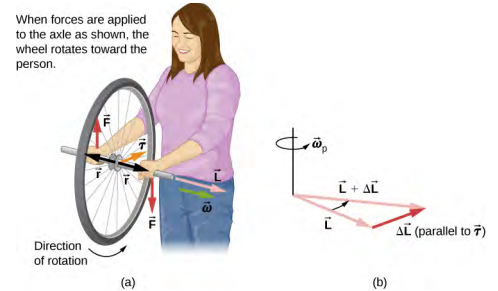
    Na figura a, uma mulher, de frente para o espectador, está segurando uma roda giratória de bicicleta de raio r pelo eixo. A roda é de forma que a velocidade angular ômega e o momento angular L estejam ao longo do eixo de rotação da roda, à esquerda dela (a direita do espectador). Ou seja, o movimento da roda é tal que a parte inferior da roda está se movendo em direção a ela (na página). A direção da força F aplicada pela mão esquerda é mostrada para baixo e a da mão direita na direção ascendente. O torque tau está voltado para ela (na página). Na figura b, é mostrada a adição de dois vetores L e delta-L, que são paralelos ao torque tau. A resultante dos dois vetores é rotulada como L mais delta L. A direção de rotação, ômega sub p, é no sentido anti-horário, conforme visto de cima.
    Figura\(\PageIndex{4}\): (a) Uma pessoa segurando a roda giratória da bicicleta a levanta com a mão direita e empurra para baixo com a mão esquerda na tentativa de girar a roda. Essa ação cria um torque diretamente em direção a ela. Esse torque causa uma mudança no momento angular exatamente\(\Delta \vec{L}\) na mesma direção. (b) Um diagrama vetorial que descreve como\(\Delta \vec{L}\) e\(\vec{L}\) adiciona, produzindo um novo momento angular apontando mais para a pessoa. A roda se move em direção à pessoa, perpendicularmente às forças que ela exerce sobre ela.

    Todos nós sabemos como é fácil tombar uma bicicleta quando está sentada nela em repouso. Mas ao andar de bicicleta em um bom ritmo, é mais difícil tombá-la porque precisamos mudar o vetor de momento angular das rodas giratórias.

    Nota

    Assista a este vídeo sobre a precessão do giroscópio para uma demonstração completa da precessão da roda da bicicleta.

    Além disso, quando um disco giratório é colocado em uma caixa, como um reprodutor de Blu-Ray, tente movê-lo. É fácil traduzir a caixa em uma determinada direção, mas difícil girá-la em torno de um eixo perpendicular ao eixo do disco giratório, pois estamos colocando um torque na caixa que fará com que o vetor de momento angular do disco giratório se processe.

    Podemos calcular a taxa de precessão do topo na Figura\(\PageIndex{3}\). Na Figura\(\PageIndex{3}\), vemos que a magnitude do torque é

    \[\tau = rMg \sin \theta \ldotp\]

    Assim,

    \[dL = rMg \sin \theta dt \ldotp\]

    O ângulo pelo qual a parte superior processa no tempo dt é

    \[d \phi = \frac{dL}{L \sin \theta} = \frac{rMg \sin \theta}{L \sin \theta} dt = \frac{rMg}{L} dt \ldotp\]

    A velocidade angular de precessão é\(\omega_{P} = \frac{d \phi}{dt}\) e, a partir dessa equação, vemos que

    \[\omega_{P} = \frac{rMg}{L} \ldotp\]

    ou, já que L = I\(\omega\),

    \[\omega_{P} = \frac{rMg}{I \omega} \ldotp \label{11.12}\]

    Nessa derivação, assumimos que\(\omega_{P}\) <<\(\omega\), ou seja, que a velocidade angular de precessão é muito menor que a velocidade angular do disco do giroscópio. A velocidade angular de precessão adiciona um pequeno componente ao momento angular ao longo do eixo z. Isso é visto em uma leve oscilação para cima e para baixo à medida que o giroscópio se precessa, conhecido como nutação.

    A própria Terra age como um giroscópio gigantesco. Seu momento angular está ao longo de seu eixo e atualmente aponta para Polaris, a Estrela Polar. Mas a Terra está lentamente precessando (uma vez em cerca de 26.000 anos) devido ao torque do Sol e da Lua em sua forma não esférica.

    Exemplo\(\PageIndex{1}\): Period of Precession

    Um giroscópio gira com a ponta no chão e gira com uma resistência ao atrito insignificante. O disco do giroscópio tem massa de 0,3 kg e gira a 20 rotações/s, seu centro de massa está a 5,0 cm do pivô e o raio do disco é 5,0 cm. Qual é o período de precessão do giroscópio?

    Estratégia

    Usamos a Equação\ ref {11.12} para encontrar a velocidade angular de precessão do giroscópio. Isso nos permite encontrar o período de precessão.

    Solução

    O momento de inércia do disco é

    \[I = \frac{1}{2} mr^{2} = \frac{1}{2} (0.30\; kg)(0.05\; m)^{2} = 3.75 \times 10^{-4}\; kg\; \cdotp m^{2} \ldotp \nonumber\]

    A velocidade angular do disco é

    \[20.0\; rev/s = (20.0)(2 \pi)\; rad/s = 125.66\; rad/s \ldotp \nonumber\]

    Agora podemos substituir na Equação\ ref {11.12}. A velocidade angular de precessão é

    \[\omega_{P} = \frac{rMg}{I \omega} = \frac{(0.05\; m)(0.3\; kg)(9.8\; m/s^{2})}{(3.75 \times 10^{-4}\; kg\; \cdotp m^{2})(125.66\; rad/s)} = 3.12\; rad/s \ldotp \nonumber\]

    O período de precessão do giroscópio é

    \[T_{P} = \frac{2 \pi}{3.12\; rad/s} = 2.0\; s \ldotp \nonumber\]

    Significância

    A frequência angular de precessão do giroscópio, 3,12 rad/s, ou cerca de 0,5 rev/s, é muito menor do que a velocidade angular de 20 rev/s do disco do giroscópio. Portanto, não esperamos que um grande componente do momento angular surja devido à precessão, e a Equação 11.12 é uma boa aproximação da velocidade angular de precessão.

    Exercícios\(\PageIndex{1}\)

    Um topo tem uma frequência de precessão de 5,0 rad/s na Terra. Qual é sua frequência de precessão na Lua?