11.4: Conservação do momento angular
- Page ID
- 184811
- Aplique a conservação do momento angular para determinar a velocidade angular de um sistema rotativo no qual o momento de inércia está mudando
- Explicar como a energia cinética rotacional muda quando um sistema sofre mudanças no momento de inércia e na velocidade angular
Até agora, analisamos o momento angular de sistemas que consistem em partículas pontuais e corpos rígidos. Também analisamos os torques envolvidos, usando a expressão que relaciona o torque líquido externo à mudança no momento angular. Exemplos de sistemas que obedecem a essa equação incluem um pneu de bicicleta que gira livremente com o tempo devido ao torque decorrente do atrito, ou a desaceleração da rotação da Terra ao longo de milhões de anos devido às forças de atrito exercidas nas deformações das marés.
No entanto, suponha que não haja torque externo líquido no sistema,\(\sum \vec{\tau}\) = 0. Nesse caso, podemos introduzir a lei de conservação do momento angular.
O momento angular de um sistema de partículas em torno de um ponto em um quadro de referência inercial fixo é conservado se não houver torque externo líquido em torno desse ponto:
\[\frac{d \vec{L}}{dt} = 0 \label{11.10}\]
ou
\[\vec{L} = \vec{l}_{1} + \vec{l}_{2} + \cdots + \vec{l}_{N} = constant \ldotp \label{11.11}\]
Observe que o momento angular total\(\vec{L}\) é conservado. Qualquer um dos momentos angulares individuais pode mudar, desde que sua soma permaneça constante. Essa lei é análoga à conservação do momento linear quando a força externa em um sistema é zero.
Como exemplo de conservação do momento angular, a Figura\(\PageIndex{1}\) mostra um patinador de gelo executando um giro. O torque líquido dela é muito próximo de zero porque há relativamente pouco atrito entre seus patins e o gelo. Além disso, o atrito é exercido muito próximo ao ponto de articulação. Ambos\(|\vec{F}|\)\(|\vec{r}|\) são pequenos, então\(|\vec{\tau}|\) é insignificante. Consequentemente, ela pode girar por algum tempo. Ela também pode aumentar sua taxa de rotação puxando os braços e as pernas para dentro. Por que puxar os braços e as pernas aumenta sua taxa de rotação? A resposta é que seu momento angular é constante, de modo que
\[L' = L\]
ou
\[I' \omega' = I \omega,\]
onde as quantidades preparadas se referem a condições após ela ter puxado os braços e reduzido seu momento de inércia. Como I` é menor, a velocidade angular\(\omega\) ′deve aumentar para manter o momento angular constante.
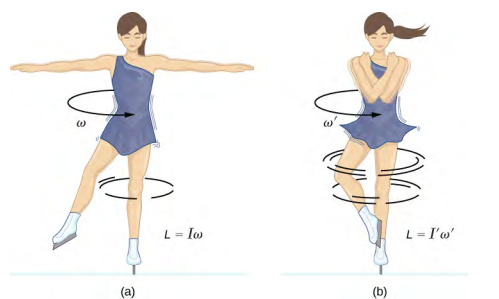
É interessante ver como a energia cinética rotacional da patinadora muda quando ela puxa os braços para dentro. Sua energia rotacional inicial é
\[K_{Rot} = \frac{1}{2} I \omega^{2},\]
enquanto sua energia rotacional final é
\[K'_{Rot} = \frac{1}{2} I (\omega')^{2} \ldotp\]
Como\(\omega\) I′′` = I\(\omega\), podemos substituir por\(\omega\) ′e encontrar
\[K'_{Rot} = \frac{1}{2} I' (\omega')^{2} = \frac{1}{2} I' \left(\dfrac{I}{I'} \omega \right)^{2} = \frac{1}{2} I \omega^{2} \left(\dfrac{I}{I'}\right) = K_{Rot} \left(\dfrac{I}{I'}\right) \ldotp\]
Como seu momento de inércia diminuiu\(I′ < I\), sua energia cinética rotacional final aumentou. A fonte dessa energia cinética rotacional adicional é o trabalho necessário para puxar seus braços para dentro. Observe que os braços do patinador não se movem em um círculo perfeito — eles espiralam para dentro. Este trabalho causa um aumento na energia cinética rotacional, enquanto seu momento angular permanece constante. Como ela está em um ambiente sem atrito, nenhuma energia escapa do sistema. Assim, se ela estendesse os braços até suas posições originais, ela giraria em sua velocidade angular original e sua energia cinética retornaria ao seu valor original.
O sistema solar é outro exemplo de como a conservação do momento angular funciona em nosso universo. Nosso sistema solar nasceu de uma enorme nuvem de gás e poeira que inicialmente tinha energia rotacional. As forças gravitacionais fizeram com que a nuvem se contraisse e a taxa de rotação aumentasse como resultado da conservação do momento angular (Figura\(\PageIndex{2}\)).
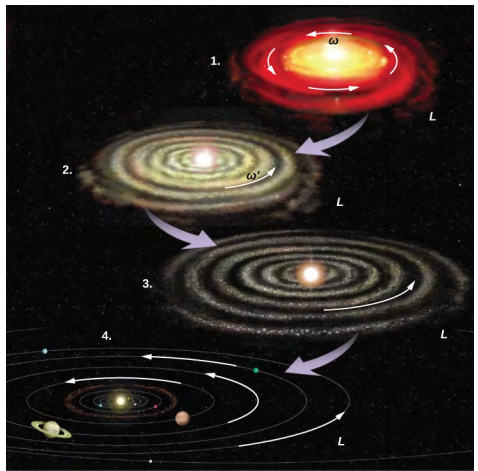
Continuamos nossa discussão com um exemplo que tem aplicações em engenharia.
Um volante gira sem atrito a uma velocidade angular\(\omega_{0}\) = 600 rev/min em um eixo vertical sem atrito de inércia rotacional insignificante. Um segundo volante, que está em repouso e tem um momento de inércia três vezes maior que o do volante giratório, é jogado sobre ele (Figura\(\PageIndex{3}\)). Como existe atrito entre as superfícies, os volantes atingem muito rapidamente a mesma velocidade de rotação, após a qual giram juntos.
- Use a lei da conservação do momento angular para determinar a velocidade angular\(\omega\) da combinação.
- Qual fração da energia cinética inicial é perdida no acoplamento dos volantes?
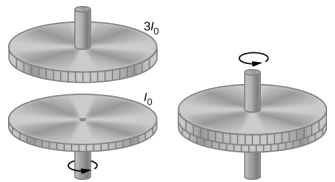
Estratégia
A parte (a) é fácil de resolver para a velocidade angular do sistema acoplado. Usamos o resultado de (a) para comparar as energias cinéticas inicial e final do sistema em parte (b).
Solução
- Nenhum torque externo atua no sistema. A força devido ao atrito produz um torque interno, que não afeta o momento angular do sistema. Portanto, a conservação do momento angular dá\[I_{0} \omega_{0} = (I_{0} + 3I_{0}) \omega, \nonumber\]\[\omega = \frac{1}{4} \omega_{0} = 150\; rev/min = 15.7\; rad/s \ldotp \nonumber\]
- Antes do contato, apenas um volante está girando. A energia cinética rotacional desse volante é a energia cinética rotacional inicial do sistema,\(\frac{1}{2} I_{0} \omega_{0}^{2}\). A energia cinética final é\[\frac{1}{2} (4I_{0}) \omega^{2} = \frac{1}{2} (4I_{0}) \left(\dfrac{\omega_{0}}{4}\right)^{2} = \frac{1}{8} I_{0} \omega_{0}^{2}. \nonumber\] Portanto, a razão entre a energia cinética final e a energia cinética inicial é\[\frac{\frac{1}{8} I_{0} \omega_{0}^{2}}{\frac{1}{2} I_{0} \omega_{0}^{2}} = \frac{1}{4} \ldotp \nonumber\] Assim, 3/4 da energia cinética inicial é perdida no acoplamento dos dois volantes.
Significância
Como a inércia rotacional do sistema aumentou, a velocidade angular diminuiu, conforme esperado pela lei de conservação do momento angular. Neste exemplo, vemos que a energia cinética final do sistema diminuiu, à medida que a energia é perdida no acoplamento dos volantes. Compare isso com o exemplo da patinadora em Figure\(\PageIndex{1}\) trabalhando para trazer os braços para dentro e adicionar energia cinética rotacional.
Um carrossel em um playground gira a 4,0 rotações/min. Três crianças pulam e aumentam o momento de inércia do sistema rotativo carrossel para crianças em 25%. Qual é a nova taxa de rotação?
Uma ginasta de 80,0 kg desmonta de uma barra alta. Ele inicia a desmontagem em extensão total e, em seguida, dobra para completar várias rotações antes de pousar. Seu momento de inércia quando totalmente estendido pode ser aproximado como uma haste de 1,8 m de comprimento e, quando na dobra, uma haste de metade desse comprimento. Se sua taxa de rotação em extensão total for de 1,0 rotações/s e ele entrar na dobra quando seu centro de massa estiver a 3,0 m de altura movendo-se horizontalmente para o chão, quantas rotações ele pode executar se sair da dobra a 1,8 m de altura? Veja a Figura\(\PageIndex{4}\).
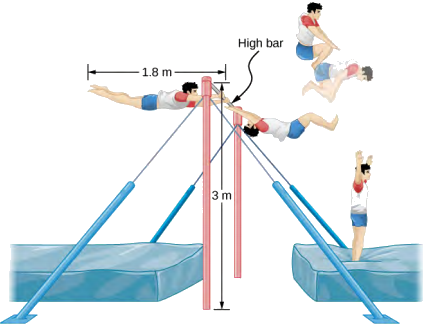
Estratégia
Usando a conservação do momento angular, podemos encontrar sua taxa de rotação quando estamos na dobra. Usando as equações da cinemática, podemos encontrar o intervalo de tempo de uma altura de 3,0 m a 1,8 m. Como ele está se movendo horizontalmente em relação ao solo, as equações de queda livre simplificam. Isso permitirá que o número de revoluções que podem ser executadas seja calculado. Como estamos usando uma proporção, podemos manter as unidades em rev/s e não precisamos converter em radianos/s.
Solução
O momento de inércia em plena extensão é\[I_{0} = \frac{1}{12} mL^{2} = \frac{1}{12} (80.0\; kg)(1.8\; m)^{2} = 21.6\; kg\; \cdotp m^{2} \ldotp \nonumber\]
O momento de inércia na dobra é\[I_{f} = \frac{1}{12} mL_{f}^{2} = \frac{1}{12} (80.0\; kg)(0.9\; m)^{2} = 5.4\; kg\; \cdotp m^{2} \ldotp \nonumber\]
Conservação do momento angular:\[I_{f} \omega_{f} = I_{0} \omega_{0} \Rightarrow \omega_{f} = \frac{I_{0} \omega_{0}}{I_{f}} = \frac{(21.6\; kg\; \cdotp m^{2})(1.0\; rev/s)}{5.4\; kg\; \cdotp m^{2}} = 4.0\; rev/s \ldotp \nonumber\]
Intervalo de tempo na dobra:\[t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2(3.0 - 1.8) m}{9.8\; m/s}} = 0.5\; s \ldotp \nonumber\]
Em 0,5 s, ele poderá executar duas revoluções a 4,0 rotações/s.
Significância
Observe que o número de revoluções que ele pode completar dependerá de quanto tempo ele estiver no ar. No problema, ele está saindo da barra alta horizontalmente em direção ao chão. Ele também poderia sair em um ângulo em relação ao solo, dando-lhe mais ou menos tempo no ar, dependendo do ângulo, positivo ou negativo, em relação ao solo. Os ginastas devem levar isso em consideração ao executar suas desmontagens.
Uma bala de massa m = 2,0 g está se movendo horizontalmente com uma velocidade de 500,0 m/s. A bala atinge e fica embutida na borda de um disco sólido de massa M = 3,2 kg e raio R = 0,5 m. O cilindro é livre para girar em torno de seu eixo e está inicialmente em repouso (Figura\(\PageIndex{5}\)). Qual é a velocidade angular do disco imediatamente após o projétil ser incorporado?
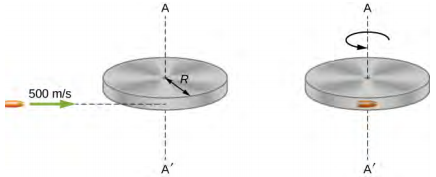
Estratégia
Para o sistema da bala e do cilindro, nenhum torque externo atua ao longo do eixo vertical que passa pelo centro do disco. Assim, o momento angular ao longo desse eixo é conservado. O momento angular inicial da bala é MvR, que é medido em torno do eixo rotacional do disco no momento anterior à colisão. O momento angular inicial do cilindro é zero. Assim, o momento angular líquido do sistema é MvR. Como o momento angular é conservado, o momento angular inicial do sistema é igual ao momento angular da bala embutida no disco imediatamente após o impacto.
Solução
O momento angular inicial do sistema é
\[L_{i} = mvR \ldotp \nonumber\]
O momento de inércia do sistema com a bala embutida no disco é
\[I = mR^{2} + \frac{1}{2} MR^{2} = \left(m + \dfrac{M}{2}\right) R^{2} \ldotp \nonumber\]
O momento angular final do sistema é
\[L_{f} = I \omega_{f} \ldotp \nonumber\]
Assim, pela conservação do momento angular, L i = L f e
\[mvR = \left(m + \dfrac{M}{2}\right) R^{2} \omega_{f} \ldotp \nonumber\]
Resolvendo para\(\omega_{f}\),
\[\omega_{f} = \frac{mvR}{\left(m + \dfrac{M}{2}\right) R^{2}} = \frac{(2.0 \times 10^{-3}\; kg)(500.0\; m/s)}{(2.0 \times 10^{-3}\; kg + 1.6\; kg)(0.50\; m)} = 1.2\; rad/s \ldotp \nonumber\]
Significância
O sistema é composto por uma partícula pontual e um corpo rígido. Deve-se ter cuidado ao formular o momento angular antes e depois da colisão. Pouco antes do impacto, o momento angular da bala é medido em torno do eixo rotacional do disco.


